Topological Complexity of Blowup Problems
Robert Rettinger (University of Hagen, Germany)
Klaus Weihrauch (University of Hagen, Germany)
Ning Zhong (University of Cincinnati, Germany)
Abstract: Consider the initial value problem of the first-order ordinary differential equation
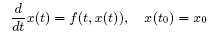
where the locally Lipschitz continuous function 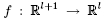 with open domain and the initial datum (t0, x0) ∈ with open domain and the initial datum (t0, x0) ∈ 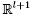 are given. It is shown that the solution operator producing the maximal "time" interval of existence and the solution on it is computable. Furthermore, the topological complexity of the blowup problem is studied for functions f defined on the whole space. For each such function f the set Z of initial conditions (t0, x0) for which the positive solution does not blow up in finite time is a are given. It is shown that the solution operator producing the maximal "time" interval of existence and the solution on it is computable. Furthermore, the topological complexity of the blowup problem is studied for functions f defined on the whole space. For each such function f the set Z of initial conditions (t0, x0) for which the positive solution does not blow up in finite time is a 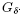 -set. There is even a computable operator determining Z from f. For l ≥ 2 this upper -set. There is even a computable operator determining Z from f. For l ≥ 2 this upper 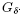 -complexity bound is sharp. For l = 1 the blowup problem is simpler. -complexity bound is sharp. For l = 1 the blowup problem is simpler.
Keywords: Type-2 theory, blowup, differential equation
Categories: F.2.1
|