|
Computing the Solution Operators of Symmetric Hyperbolic Systems of PDE
Svetlana Selivanova (Siberian Division of the Russian Academy of Sciences, Russia)
Victor Selivanov (Siberian Division of the Russian Academy of Sciences, Russia)
Abstract: We study the computability properties of symmetric hyperbolic systems of PDE 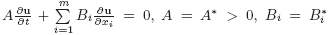 , with the initial condition , with the initial condition 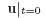 = φ(x1,...,xm). Such systems first considered by K.O. Friedrichs can be used to describe a wide variety of physical processes. Using the difference equations approach, we prove computability of the operator that sends (for any fixed computable matrices A, B1, ..., Bm satisfying certain conditions) any initial function φ ∈ Cp+1(Q, ℝn) (satisfying certain conditions), p ≥ 2, to the unique solution u ∈ Cp(H, ℝn), where Q = [0,1]m and H is the nonempty domain of correctness of the system. = φ(x1,...,xm). Such systems first considered by K.O. Friedrichs can be used to describe a wide variety of physical processes. Using the difference equations approach, we prove computability of the operator that sends (for any fixed computable matrices A, B1, ..., Bm satisfying certain conditions) any initial function φ ∈ Cp+1(Q, ℝn) (satisfying certain conditions), p ≥ 2, to the unique solution u ∈ Cp(H, ℝn), where Q = [0,1]m and H is the nonempty domain of correctness of the system.
Keywords: PDE, computability, difference scheme, finite-dimensional approximation, hyperbolic system, matrix pencil, metric space, norm, stability
Categories: F.2, F.2.1
|