Investigations on a Pedagogical Calculus of Constructions
Loïc Colson (LITA, University of Lorraine, France)
Vincent Demange (LITA, University of Lorraine, France)
Abstract: In the last few years appeared pedagogical propositional natural deduction systems. In these systems one must satisfy the pedagogical constraint: the user must give an example of any introduced notion. In formal terms, for instance in the propositional case, the main modification is that we replace the usual rule (hyp) by the rule (p-hyp) 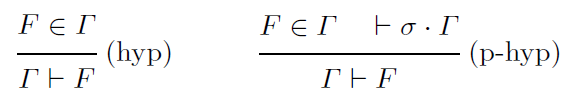 where σ denotes a substitution which replaces variables of Γ with an example. This substitution σ is called the motivation of Γ. First we expose the reasons of such a constraint and properties of these "pedagogical" calculi: the absence of negation at logical side, and the "usefulness" feature of terms at computational side (through the Curry-Howard correspondence). Then we construct a simple pedagogical restriction of the calculus of constructions (CC) called CCr. We establish logical limitations of this system, and compare its computational expressiveness to Gödel system T. Finally, guided by the logical limitations of CCr, we give a formal and general definition of a pedagogical calculus of constructions.
Keywords: calculus of constructions, constructive mathematics, mathematical logic, negationless mathematics, pedagogical system, typed lambda-calculus
Categories: F.1.1, F.4.1
|
