The Riesz Representation Operator on the Dual of C[0; 1] is Computable

Tahereh Jafarikhah (University of Tarbiat Modares, Iran)

Klaus Weihrauch (University of Hagen, Germany)

Abstract: By the Riesz representation theorem, for every linear functional F : C[0; 1] → ℝ there is a function g : [0; 1] → ℝ of bounded variation such that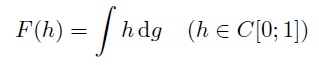

A computable version is proved in [Lu and Weihrauch(2007)]: a function g can be computed from F and its norm, and F can be computed from g and an upper bound of its total variation. In this article we present a much more transparent proof. We first give a new proof of the classical theorem from which we then can derive the computable version easily. As in [Lu and Weihrauch(2007)] we use the framework of TTE, the representation approach for computable analysis, which allows to define natural concepts of computability for the operators under consideration.

Keywords: Riesz representation theorem, computable analysis

Categories: F.0, F.1.1