|
Perhaps the Intermediate Value Theorem
Wim Veldman (Institute for Mathematics, Astrophysics and Particle
Physics, Faculty of Science, Radboud University Nijmegen, the Netherlands)
Abstract: In the context of intuitionistic real analysis, we introduce the set 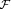 consisting of all continuous functions φ from [0, 1] to consisting of all continuous functions φ from [0, 1] to  such that φ(0) = 0 and φ(1) = 1. We let such that φ(0) = 0 and φ(1) = 1. We let 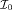 be the set of all φ in be the set of all φ in 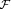 for which we may find x in [0, 1] such that φ(x) = for which we may find x in [0, 1] such that φ(x) = 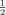 . It is well-known that there are functions in . It is well-known that there are functions in 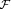 that we can not prove to belong to that we can not prove to belong to 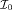 , and that, with the help of Brouwer's Continuity Principle one may derive a contradiction from the assumption that , and that, with the help of Brouwer's Continuity Principle one may derive a contradiction from the assumption that 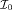 coincides with coincides with 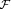 . We show that Brouwer's Continuity Principle also enables us to define uncountably many subsets . We show that Brouwer's Continuity Principle also enables us to define uncountably many subsets 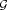 of of 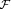 with the property with the property 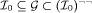 . .
Keywords: intermediate value theorem, intuitionistic real analysis, perhaps
Categories: G.0
|