Constructive Set Theory and Brouwerian Principles

Michael Rathjen (Department of Mathematics, The Ohio State University, USA)

Abstract: The paper furnishes realizability models of constructive Zermelo-Fraenkel set theory, CZF, which also validate Brouwerian principles such as the axiom of continuous choice (CC), the fan theorem (FT), and bar induction (BI), and thereby determines the proof-theoretic strength of CZF augmented by these principles.
The upshot is that CZF+CC+FT possesses the same strength as CZF, or more precisely, that CZF+CC+FT is conservative over CZF for 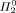statements of arithmetic, whereas the addition of a restricted version of bar induction to CZF (called decidable bar induction, BI^D) leads to greater proof-theoretic strength in that CZF+BI^D proves the consistency of CZF.

Keywords: Brouwerian principles, constructive set theory, partial combinatory algebra, realizability

Categories: F.4.1