| Submission Procedure |
A Reference Model for Security Level Evaluation: Policy and Fuzzy TechniquesValentina Casola Rosa Preziosi Massimiliano Rak Luigi Troiano Abstract: In a world made of interconnected systems which manage huge amounts of confidential and shared data, security plays a significant role. Policies are the means by which security rules are defined and enforced. The ability to evaluate policies is becoming more and more relevant, especially when referred to the cooperation of services belonging to untrusted domains. We have focused our attention on Public Key Infrastructures (PKIs); at the state of the art security policies evaluation is manually performed by technical and organizational people coming from the domains that need to interoperate. However, policy evaluation must face uncertainties derived from different perspectives, verbal judgments and lack of information. Fuzzy techniques and uncertainty reasoning can provide a meaningful way for dealing with these issues. In this paper we propose a fuzzy technique to characterize a policy and to define a Reference Evaluation Model representing different security levels against which we are able to evaluate and compare policies. The comparison takes into account not only minimal system needs but evaluator's severity, too; furthermore it gives clear information regarding policy weakness that could be used to help security administrators to better enforce rules. Finally we present a case study which evaluates the security level of a "legally recognized" policy. Key Words: Policy, Public Key Infrastructure, Security Evaluation, Fuzzy Techniques Page 150 1 IntroductionIn recent years, due to the large diffusion of distributed systems, there has been a large need for security grants to fully trust a system. To achieve this goal, it is necessary that systems which produce and exchange documents (especially digitally signed and legally recognized documents) should be able to guarantee a certain "security level" and demonstrate their trust ability. The problem of resource sharing among wide infrastructures is relatively new in Computer Science; in most classical architectures, shared resources are part of one system with one centralized security mechanism enforcing access control rules. In contrast, a distributed architecture is composed of several subsystems representing specific domains and each one has to face its own security issues; to let them interoperate, mechanisms must be found to integrate them. These mechanisms, of course, involve heavy security management issues which could make the whole system weak. In this paper we focus on Public Key Infrastructures (PKI) [Housley, 1999, Ford, 1997, Curry, 2000] and on the rules that a Certification Authority (CA) has to follow or implement to guarantee a certain "security level" to the users certified in its domain. The need for a clear definition and selection of security rules has led system administrators to formally face system security and management by means of policies which are composed of a set of security rules and allow:
Since a formal definition of Security Level does not exist in literature, this represents a big problem to face [Lupu, 1999, Casola, 2002] because it is not possible to extend trust to other domains based on assertions like: " the system is secure enough to...". To face this problem we think that it is possible to start from security policies to formally describe the behavior of a system, and so formally characterize all security critical aspects. After formalization, the "extending trust" issue (cross certification [NIST, 2001, Turnbull, 2000]) could be performed through policy evaluation and comparison [Grill, 2000]. In this paper we propose a security policy evaluation technique to handle such problems; we will focus on certificate policies of Public Key Infrastructures (PKIs) but the technique is not limited to this field. Our start points are:
Page 151 A CP template to formalize provisions in an unambiguous way has been presented in [Casola, 2002, Casola, 2003] where each technical and nottechnical provision is represented as a numeric or enumerative datatype. The formalized policy is a structured set of all provision instances. It is very useful to write a policy and immediately locate different provisions between the two policies but, a global evaluation mechanism was never proposed. Since policies are usually written in free textual words, an effective policy evaluation cannot avoid dealing with the semantics of free textual words. This fact inspired us to adopt fuzzy models to better address this aspect [Hosmer, 1992] and to propose a fuzzybased policy evaluation technique. Through fuzzification we gain a higher expressive power, an enhanced ability to model realworld problems, and, above all, a methodology for exploit ing the tolerance for imprecision. By allowing soft analysis, fuzzy set theory [Zadeh, 1965] does not force precision where it is not possible as other approaches did. Fuzzy sets have a natural capability to express and deal with observation and measurement uncertainties, they are more attuned to reality than crisp sets [Klir, 1995]. In a security context, fuzzy numbers allow us to represent whether or not a security provision is guaranteeing an expected security level through a verbal judgement; this will help us to better model vagueness of words and judgments related to technical and nontechnical provisions. In particular, each security provision can be assessed with an ordinal judgment label used in our approach to define a fuzzy number for each provision. The most important result of this approach is that the overall policy evaluation will be obtained by aggregating fuzzy values representative of security provision assessment. The remainder of this paper is structured as follows: in Sections 2 and 3 we will illustrate the context in which the certificate policy evaluation could be a big problem to face for Cross Certification, and we will illustrate our approach for policy formalization to help security administrators in performing such an evaluation. In Section 4 we will illustrate some details regarding the fuzzy theory and how we have used it to characterize and analyze a policy. In Section 5, a Reference Evaluation Model is proposed to evaluate and compare policies. In Section 6 a case study is presented to illustrate and validate all the steps of the proposed technique through an example of policy comparison. Finally the proposed technique is briefly summarized and some conclusions are presented. Page 152 2 Security BackgroundAccording to RFC2459, a certificate policy is "a named set of rules that indicates the applicability of a certificate to a particular community and/or class of application with common security requirements" [Housley, 1999]. At present, a certificate policy standard does not exist; in the PKI field, this is a very huge problem, especially during the comparison process, when two different Certification Authorities (CAs) need to extend trust to each others in order to allow interoperability among their users and, at the same time, guarantee the declared security levels. The action of extending trust is usually referred to as Cross Certification and it usually involves the cooperation of both technical and organizational people from the CAs that need to trust the other parties in order to completely understand if they are able to interoperate in terms of technological implications and are able to guarantee the same security level to their users. This problem is currently dealt with as an "organizational problem": security experts, from both the technological and the organizational field, manually evaluate the different provisions implemented by the two CAs and, by manually comparing each provision, they finally decide to cross certify them or not. The novelty of digital signature technology and the diverse perspectives of policy makers, including legislators, industry representatives, and the organized association, have resulted in divergent approaches for resolving key issues within different jurisdictions; for this reason, up to few years ago, there were very different models of certificate policies. In particular, the policies were different with regard to their structures and with regard to the critical provisions included in them; indeed, each organization could decide which technologies to adopt and above all the liabilities and responsibilities involved in the use of digital signatures (for example that in Italy a digital signature has "legal validity"). Cross Certification is not simple at all, since it involves not only technological aspects (partially resolved by the standard X.509 [Housley, 1999], PKCS families , and so on) but, above all, organizational and liabilitiesrelated aspects. There are a lot of examples available on the Internet [Curry, 2000, Turnbull, 2000] in which, to simplify their work, each CA builds a table with all its critical security provisions on the rows and, on the columns, they respectively put the provision instances implemented by the two CAs and only after an accurate evaluation of all of them, they could decide to cross certify or not. In addition the building and evaluation of this table is not simple, because it is not obvious that the two CAs consider critical the same provisions and it is not obvious that technical and organizational people agree on the evaluation of the single provisions. Page 153 As previously mentioned, there is no standard format, standard list of topics, or standard procedures for a policy; nevertheless, because the provisions of different policies need to be compared, we need a commonlyagreed approach to structure the policy contents, in order to quickly identify their similarities and differences. We therefore need a structured and formalized policy model, to:
Furthermore, it is much easier to compare policies if they are presented not only in a unique structured way but also if the very complex objects described are formalized as simple types; in this way, in fact, it would be possible to establish some logical relations or comparison criteria among them. In the following sections we will illustrate a way to formally represent a policy and a fuzzy technique to automatically evaluate it. 3 Policy FormalizationIn this section we report some results of previous works on policy formalization since we will use them to implement the technique of the next section. As previously mentioned, a certificate policy standard does not exist. Recently, some efforts to formalize PKIs certificate policies and related security provisions have been produced; the formalizations proposed in [Mendes, 1995, Klobucar, 1999, Casola, 2002, Casola, 2003] help system and security administrators in the policy life cycle management. In effect, all policy frameworks present wide limits; they certainly represent a valid means for developing a textual policy, but they do not resolve ambiguity problems, they are not sufficiently structured to be used as a valid means for evaluating and comparing policies. Probably, as mentioned before, the most detailed and relevant suggestion for the formal presentation of certificate policies was described in the Internet RFC3647 [Chokhani, 1999]. It is not a standard but it is currently widely used by all the Internet Community and for all these reasons we have decided to choose its main provisions and structure for the first steps of our formalization. We primarily underline that the framework is structured as a hierarchical tree. Textual provisions were refined in a finegrain and a grammar to automatically compare them was proposed in [Casola, 2002]. We will adopt this approach to define a policy formalization, it consists of three steps: Page 154 Step 1) definition of macroprovisions; Step 2) definition of second level provisions; Step 3) XML language definition. As mentioned above, the RFC3647 is a good example of policy formalization so we have decided to use its structure to implement the first two steps of our method. All the macroprovisions are very complex objects, categorized for different topics, which need to be addressed in a Certificate Policy. According to the RFC3647, the first level of provisions includes:
Second level provisions try to describe all the details regarding all macroprovisions and they express objects which are still complex but bring more bounded security information; for example the Technical Security Control provision includes: Key Pair Generation, Private Key Protection, Other Aspects of Key Pair Management, Activation Data, Computer Security Controls, Life Cycle Technical Control, Network Security Control, Cryptographic module engineering controls. At this point we have defined the main provisions of our structure which are actually filled with textual descriptions. The provisions defined in the first two steps are very complex objects and this is the most important reason of ambiguity; to solve ambiguities, the proposed model supports a hierarchical structure which consists of several couples (elementtype, value) representing topics and subtopics, where the "value" itself is a complex object. A wide range of new datastructures has been defined to represent the values, and finally a grammar has been created based on such a datastructure set to formalize a certificate policy. The datastructures used are new atomic or enumerative types and total order relations among their values may be defined, so as to solve the ambiguity problem. For most critical topics we were able to build such a structure which could be automatically processed by a numeric algorithm. Page 155 The proposed structure is a hierarchical tree which can be represented by an XML document; tree nodes identify complex security provisions, leaves identify simple security provisions [Casola, 2002, Chokhani, 1999, Casola, 2004]. Now we will present some significant examples. Example 1. XML Structure of the provision: Private Key Protection: <PrivateKeyProtection>
........
<PrivateKeyProtectionBOX>
<PrivateKeyNoProtection>...</PrivateKeyNoProtection>
<PrivateKeyOnLocalPC>...</PrivateKeyOnLocalPC>
<PrivateKeyOnFloppy>...</PrivateKeyOnFloppy>
<PrivateKeyOnSmartCard>...</PrivateKeyOnSmartCard>
<PrivateKeyOnSmartCardWithBiometricSensor>......
</PrivateKeyOnSmartCardWithBiometricSensor>
</PrivateKeyProtectionBOX>
.......
<PrivateKeyEscrow>...</PrivateKeyEscrow>
<PrivateKeyBackup>...</PrivateKeyBackup>
</PrivateKeyProtection>
Example 2. XML Structure of the provision: Publication Repository: <PublicationRepository>
.......
<FrequencyPublication>
< PolicyIssuanceFrequency>...</ PolicyIssuanceFrequency>
< PublishedCertificateIssuanceFrequency>...
</ PublishedCertificateIssuanceFrequency>
< CRLIssuanceFrequency>...</ CRLIssuanceFrequency>
< FrequencyDay>...</ FrequencyDay >
<FrequencyHours>...</FrequencyHours >
<FrequencyMinutes>...</ FrequencyMinutes >
<FrequencySeconds>...</ FrequencySeconds >
</FrequencyPublication>
........
</PublicationRepository>
Page 157 Based on the elements of Example 1 and 2, being enumerative or numerical types, it is possible to define a total order relation. Thanks to the tree structure of the document, in which every "textual" provision or any other data element is represented by a specific node which has to be father, child or brother of any other node element, it has been possible to represent the relationships among the elements of the policy without any ambiguity. As shown, there are some very simple types that primarily correspond to quantifiable parameters (key length, CRL publication period, etc), they are usually used in available literature when comparing policies. Other elements have a more complex and structured representation and the applicability of our method to these elements is the main contribution of our formalization. We have used it to easily compare "single statements" by using a simple XML parser; however the process is still semiautomated, it could help when:
Indeed, the main feature of that approach is that it enforces a formalization even on nonnumerical provisions, this is the case for a lot of organizational and nontechnical provisions whose semantic usually carries very critical information; the risk of a discrete formalization is the inevitable loss of information; for this reason, we decided to adopt a fuzzy technique which is capable of dealing with uncertainties of words. 4 Policy Fuzzy CharacterizationProposed formalization helps us to highlight all the security provisions that a CA has to assure. We need, now, a way to express a judgement regarding the overall quality of a given instance of the policy, in order to compare and classify different proposed policy instances. In order to derive the overall evaluation of PKI security policies, we need to aggregate successively all simple provision evaluations to obtain a final global judgement. The final judgement, that is the aggregating result, should be:
4.1 The Problem of Policy EvaluationEffective security of systems for an organization is not easily quantifiable and/or qualifiable: the evaluation of security policies must deal with the evaluation of security technical provisions which are partially qualitative and therefore uncertain. The main issue is to define a suitable model capable of aggregating the evaluation of each provision into a reliable index expressing the policy quality. Indeed, we could mainly view this as a MultiCriteria Decision Making (MCDM) problem [Bellman, 1970]. The simplest way for dealing with MCDM problems consists in transforming qualitative assessments into numbers, in order to aggregate them with quantitative information, usually by means of minimum (min), maximum (max) or weighted averaging (wa). An example can be useful: let us consider only two security provisions: <KeyDmension> and <SignatureAlgorithm>, where the first one is evaluated as good and the second one as bad ; a "minimum" aggregator will say that the policy is bad, a "maximum" aggregator will give a final evaluation of good and a "weighted averaging" aggregator will give an intermediate judgement such as sufficient. Min, max and wa can be considered special cases of aggregation operators [Calvo, 2002]. An aggregation operator is a map: Fn : Kn -> K (1) Where K is the (numerical) set wherein assessments are expressed. Usually it coincides with an interval of numbers; often it is made up of numbers bounded in [0,1]. Aggregators must respect some axioms, such as:
Another way for dealing with MCDM problems consists of aggregating data on a continuum built along an ideal line of increasing optimism from min to max operator. This method is suitable for managing and resolving intermediate situations between severe and indulgent decision making attitudes. A wellknown class of aggregation operators is Ordered Weighted Averaging (OWA) [Yager, 1988, Yager, 1993]. An OWA operator is defined as: F(a1, ..., an = where p(.) is a decreasing ordered permutation of n elements
a1, . . . , an. Weights wi
Page 158 They express how much we wish to put into prominence best (worst) results
and are not related to the importance of the elements. An important measure
associated to OWA operators is orness (
The orness varies within [0,1] according to weight distribution. Such a relationship is not one to one: different distributions can lead to the same orness. There are three important special cases of weight distribution worth
pointing out. When wn = 1 and All aggregations always lie between min operator and max operator, previously defined, moving through the arithmetic mean. We can refer to the orness value as a measure of evaluation severity. For example, the more the orness value is low, the more the aggregation is close to a min operator and the more the evaluation will be severe. Thus when we move from the arithmetic mean to min operator, that is
to wards a lower orness, the trust in the aggregation increases; in
any case we should not pass the level of 4.2 Fuzzy JudgementsMoreover, evaluation of policies should deal with uncertainty of qualitative assessments which cannot be modelled by usual (crisp) numbers. Fuzzy numbers are more suitable for capturing and representing the imprecision of technical and non technical provisions. For example, imagine that an evaluator considers the clause <ContactDetails> which contains the name of the person in charge of the policy and he wants to compare two instances of a given policy which differ with regard to the name the person in charge. Page 159 In particular the evaluator might need to point out which person in charge is more reliable, that is the evaluator needs to express a judgement on the quality of the person in charge. In this case fuzzy judgements are a big help in the evaluation. Fuzzy set theory provides an exact representation of concepts and relations which are vague or imprecise. This theory, with the associated logic, named fuzzy logic, was proposed by [Zadeh, 1965]. A fuzzy set is a set, A (in a Universe X), without a sharp borderline contrary to classical (crisp) sets. In fact in a fuzzy set each element may belong (membership degree = 1) or not (membership degree = 0) at the set or have degrees of membership between 0 and 1 but in a crisp set elements must have either 0 or 1 as the membership degree. We are particularly interested in a special type of fuzzy sets: the fuzzy numbers, which are often represented with triangular and trapezoidal membership functions. Fuzzy numbers are largely used to express and model judgments [Bellman, 1970, Zadeh, 1972], taking into account vagueness of words and qualitative assessments. Evaluation could be made by ordinal scales. Each term of the scale is represented by a label and labels are ordered in an increasing way, too. For example if four different judgments on a single provision should be expressed, the corresponding labels could be: poor, average, good, optimal; if we assume that values can be uniformly comprised between 0 and 1, an ordinal numerical value should report poor as 0, average as 0.33, good as 0.66 and optimal as 1. Of course for each judgement we could choose a less or more finegrain scale, this is usually denoted as the granularity or resolution of the scale. By using triangular fuzzy numbers, a judgment on the scale can be represented by a pair (p,s), where p is the ordinal position of the label in the chosen scale of judgment (for example the label "good" has the 3rd ordinal position in the previous scale, so p=3) and s is the number of labels considered by the scale i.e. the granularity or the resolution of scale (in the previous example s=4). Then these pairs are translated into fuzzy numbers with triangular shape. Their shape is characterized by these characteristic points: 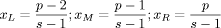 (5) (5)The distance between xL and xR determines the base of the triangular shape and xM determines its vertex orthogonal to the base. For instance if the judgment "good" is the forth on a scale of five (p= 4, s= 5), we get xL= 0.5, xM = 0.75, xR= 1.0. differently if it is the fifth on a scale of seven (p= 5, s= 7), we get xL= 0.5, xM = 0.66, xR= 0.83. Figure 1 illustrates an example of a fuzzy representation of a scale of five terms whose labels are very low, low, medium, high, very high. The top of the figure shows the verbal judgments, while the numerical values on the xaxis are the ordinal positions xL , xM and xR . Of course the triangle width depends on the scale resolution. An interesting result of this approach for modelling judgements is that the xM , named core, could be interpreted as a traditional crisp judgment, while xR xL could be interpreted as an index of the fuzziness of the judgment. Page 160 Figure 1: Triangular Fuzzy Representation of a Scale of five Terms We explicitly note that if a provision is not implemented at all in a security policy, the security system is heavily affected and a very negative judgment should be expressed on it; this situation is modelled as a particular triangular fuzzy number with xL= 0, xM = 0, xR= 0 that is with a crisp zero. With this particular number we are able to express the worst judgment (zero) with no uncertainty (crisp). 4.3 OFNWA AggregationThe aggregation operators used in our work are named Ordered Fuzzy Number Weighted Averaging (OFNWA); they were proposed in [Canfora, 2001, Canfora, 2002]. OFNWA operators are able to maintain uncertainty and incompleteness of information thanks to a built logical model where dependencies among criteria are modelled over a set of inferential rules. Thanks to the OFNWA operators, which aggregate fuzzy numbers into a fuzzy number, each policy, that is to say its single provisions, will be completely characterized by a couple of parameters:
With regard to our security context, xM will be associated to the assurance level of each policy while the support will be representative of the fuzziness related to the result on the assurance level. So, in our analysis we will show how these parameters effectively represent the security level guaranteed by a policy and we will give a securityrelated interpretation to the orness value. Page 161 Moreover, in [Canfora, 2003a] an appropriate importance model was introduced. Such model is based on the iterative application of the two following logical assertions:
The existence of this importance model is in accordance with another aspect which must be taken into account in security evaluation that is to say, the different relevance that criteria assume in the evaluation of PKI. The relevance parameter depends on the particular evaluator profile and his needs. For example, an enduser will stress differently criteria compared to a developer or a security administrator. Further, the result of OFNWA aggregation can be automatically computed according to different orness values thanks to a implemented fuzzy tool introduced in [Canfora, 2003b]. This tool offers:
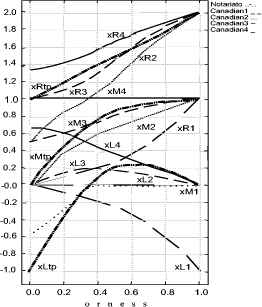
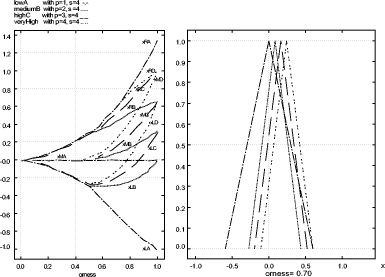
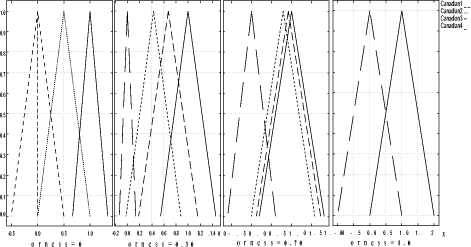
4.4 Decision GraphicsDecision graphics were proposed in [Canfora, 2003a]. An example of these graphics is shown in figure 2. From this figure an evaluator can observe graphical results of the global security level of selected policies. The related example will help the reader to understand how an evaluator could read decision graphics and highlight her/his decisions. These graphics are obtained by processing four different instances of a built evaluation graph for a given security policy. The selected instances differ only in one target provision, for which the same scale (granularity 4) and four different values low, medium, high, very high were selected. In particular we used for this provision the fuzzy numbers relative to the respective four pairs (p,s): (1,4) (2,4) (3,4) (4,4). As shown in figure 2, there are two types of graphics:
Page 162 Figure 2: Decision Graphics Example Orness variable graphics are shown on the lefthand side of figure 2 where the orness value is represented on the x axis, while the aggregation result is represented on the y axis. Since each triangular fuzzy number can be completely described by the support [x L ; xR ] and the prototypal value xM, the evaluator can analyze how these characteristic points change by changing the orness value in the interval 0 (where the evaluator's severity is maximum) and 1 (where the evaluator's severity is minimum) that is to say the evaluator can obtain three corresponding curves, changing the orness, named , xL , xR , xM . In particular in our figure we can observe four terns of these curves, one for each instance of the given policy. By analyzing these graphics, the evaluator can get information concerning the impact of the uncertainty of the initial judgements on the global security level of a selected policy measuring the distance between the curves xL and xM and the curves xM and xR . Increasing these distances, fuzziness of the evaluation grows and indeed, the use of different verbal scales, leads to results with a different degree of uncertainty too. In our figure we can observe that these distances grow by changing the orness when the value of the target provision changes. Moreover we can observe that when orness is lower than 0.5 the final judgement is not affected: when the orness is low, the severity of the evaluator is high, so even if one clause is better, the worst evaluation affects the judgement. Note that at orness 0, the evaluation is zero crisp, so there is a non stipulated provision. Page 163 The righthand side of figure 2 shows the x variable graphics. By changing the orness in the interval [0,1], the evaluator can obtain the triangular fuzzy numbers representative of the selected policies instances evaluations for each selected orness value. These graphics help the evaluator to better understand the aggregation continuum provided with OFNWA operators. Thanks to this information the security evaluator gains a better understanding of the meaning and the risk of the decisions she/he will take. The evaluator can observe that the ranking of selected different policies depends on the considered orness too. Practically, decision graphics give the security evaluator the possibility to assume a different perspective in the analysis of final results and uncertainty, and make more conscious decisions. This will be illustrated in more detail in sec. 6. 5 The Reference Evaluation ModelThanks to the proposed approach we are able to evaluate a policy, but our primary target is to compare different security policies to extend trust to other CAs or, more in general, to be able to define the security level involved with a policy. For this reason, we need a mean that helps system administrators to classify a given policy instance. Classification should be made through comparison with reference levels and their formalization. So, we define "Reference Evaluation Model" (REM) the following 4pla: REM =< P, G, S, W > where: P is a set of policy instances which represent different security levels. G is an Evaluation Graph; S is a set of scales for each leaf of the evaluation graph G; W is a collection of weights for the evaluation graph edges. The REM will contain all the information needed to classify a given policy instance against a given certification authority. In order to better explain our approach, in this paper we have chosen a particular REM where: P is the set of policy instances which represent different security levels, for our REM, we have decided to choose the four policies of the Government of Canada "Digital Signature and Confidentiality Certificate Policies for the Government of Canada PKI " [Canada Government, 1999]; as the Government itself states, they represent four different security levels whose certificates could assure four different classes of services; furthermore, these policies are structured according to the formalization of the RFC3647 so the formalization process proposed in Section 3 can be completely reused. Page 164 Figure 3: Evaluation Graph G is the Evaluation Graph defined in Section 4 whose provisions have been defined in Section 3; as previously mentioned, it was built starting from the formalization proposed in Section 3, so G is strictly related to the chosen set of policies P and the structure of the P policies is the same as the G evaluation graph. Figure 3 shows a little screenshot of the graph adopted in the following. The judgment on provisions can be chosen among labels/values expressed on scales with different granularity. Each scale represents the possible assurance levels that each security provision can guarantee: different granularity is representative of a different number of assurance levels (for each security provision). For example the provision Bit Length of the previous example is a simple nu meric provision whose typical values are: 512, 1024, 2048 bits. So, we associate a scale of just three values to this provision whose labels could be rudimentary, medium, and high; and, according to the ordinal definition introduced in [Casola, 2003], if we have a policy in which Bit Length is 1024 bit, then, we give the judgment of "medium" to this provision. Page 165
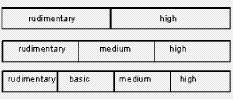
Figure 4: Verbal ordinal scales Figure 4 shows the scales used in this work; in particular we have used the following three ordinal scales:
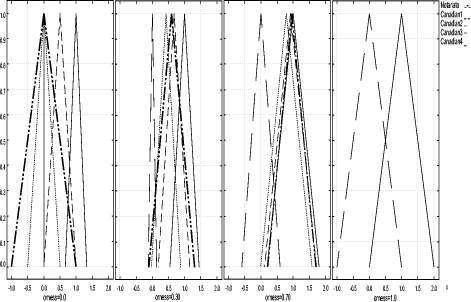
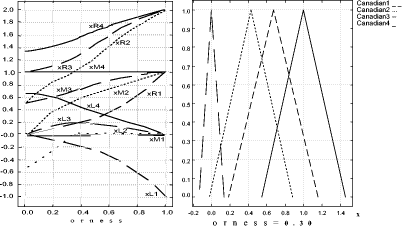
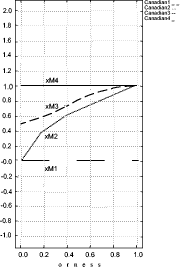
These scales have respectively a granularity of 2, 3 and 4. Technicians can provide their evaluation expressing a preference on the scale which best fits the confidence in discriminating levels. A higher availability of information can lead to a higher confidence in assessment; thus, more precise verbal ordinal scales can be adopted. By contrast, scarcity of information can lead to the choice of less precise scales. Scale values are ordinal labels, they need to be expressed in fuzzy numbers, a fuzzy triangular number is built as described in section 4, so the fuzzy number associated to the provision BitLenght= 1024 bit (medium label p= 2, s= 3) are: xL= 0, xM = 0.5, xR= 1. In conclusion, S is the map of all security provisions values in verbal judgment scales; we explicitly note that a scale needs to be defined for each provision so, like G, it depends on the chosen set of policies P. Finally, W is the set of weights, for simplicity, for this REM, we will use only weight equals to "1", the reason is simply related to the fact that we consider all provisions critical and this is the case of our set of policies. Thus, by applying the policy aggregation analysis on the set of policies P, using G as an evaluation graph, S the set of scales and W for the weights, we obtain the REM. In Figure 5 we could graphically represent the evaluated "reference policies". On the righthand side of Figure 5 we can notice the four reference security levels for a fixed DM severity level (xvariable graphics) and on the lefthand side of figure 5 the four reference security levels are mapped again but for each DM severity level (orness variable graphics). In particular, the lefthand side shows how xL, xM and xR values change, varying the orness value; this shows the behaviour of a policy against the orness: increasing the orness value and therefore decreasing the DM severity the global reference security level grows. Page 166 Figure 5: Decision Graphics for Security Policy Levels Figure 6: Decision Graphic Prototypal Values for Security Levels The righthand side graph shows the triangular fuzzy numbers with a fixed orness value (0.3). To help in evaluation understanding, we have added Figure 6, which contains only the prototypal values and Figure 7, which shows four graphics with increasing orness values (respectively 0, 0.3, 0.7 and 1). We can explicitly observe that: Page 167 a) with orness zero, the fuzzy number of level one is a zero crisp value, due to the presence of no stipulation provisions; b) lower policy has always a lower evaluation compared to higher policies c) when the orness grows, the security quality of each policy grows, but a policy of level i never exceeds a policy of level i+1. Points b) and c) exploit the correctness of the approach: policies considered more secure by a PKI, are evaluated as better policies even when the severity of the security administrator grows. Figure 7: Security Levels Decision Xvariable Graphics 6 Security EvaluationIn this section we will use the REM to evaluate a target policy. The evaluation process is composed of the following steps:
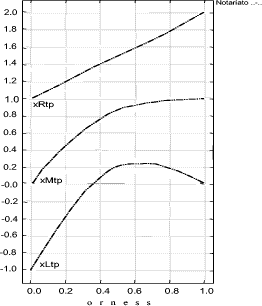
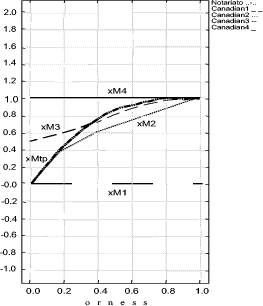
It is important to point out that the formalization process of the target policy will be carried on using the tree built on the reference system (G). With the REM we are able to evaluate a policy from the "point of view" given by the CA which has formalized the set P. In order to show the effects of this choice we will apply the described process on a real policy that comes from a completely different policy system. Page 168 Figure 8: Decision Graphic for Notariato Policy The policy we evaluate, is the "Manuale operativo del Consiglio Nazionale del Notariato" policy [Notariato Italiano, 2002]; it is an Italian policy legally recognized by the CNIPA. Italian law asserts that a digital signature is fully equivalent to a "manual" signature if the private key and the binding certificate used by the signer are issued by a legally recognized Certification Authority and the Notariato is one of them. It is important to point out that the Italian policy has a policy model different from the one adopted in Canada; for example it is written in the Italian language, it has different mandatory provisions and, furthermore, the provisions are structured in different ways. This is the biggest problem in the cross certification process, however, as already said, we dealt with it by making the policy formal through the REM G, S and W components. Mainly this has implied the adoption of the same subset of provisions and the adoption of the same judgment verbal scales to compare them with the same evaluation graph. Figure 8 shows the decision graphic (orness variable) of the Notariato policy using the G, S, W components of the REM for the aggregation. We can explicitly observe that with high severity (orness near to zero) the evaluation is zero fuzzy, really low, but it rapidly increases when the orness grows. Page 169 This is due to the fact that the Notariato policy comes from a different CA and it is built upon different security criteria. This rapid increase means that only few provisions are different from the choices of the Canada CA, but there are also provisions that are not stipulated at all and they become predominant for orness= 0. Figure 9: Decision Graphic Prototypal Values: comparison between Notariato and Security Policy Levels Figures 9 and 11 compares the Notariato policy with the set P of reference policies (the first one reports the prototypal values in the orness variable graphic, while the second shows the complete decision graphics). Figure 10 compares the Notariato policy and the reference policies with xvariable Decision graphics at orness 0, 0.3, 0.7, 1. In the following we will assume that xLtp, xMtp, xRtp is the triangular fuzzy number characterizing the Notariato policy, while xLi, xMi, xRi i = 1..4 are the reference policies fuzzy values. We can explicitly note that xL : Page 170 Figure 10: xvariables Graphics for Notariato and Security Policy Levels Figure 11: Decision Graphic: comparison between Notariato and Security Policy Levels Page 171 So if the security analyst strictly adopts the Notariato policy, it will be evaluated as level 2. But if he proceeds in the analysis he can see that the Notariato policy lies between level 2 and 3 with orness lower than 0.3, but then it lies between level 3 and 4. Our analysis underlines that a severe security analyst has to choose level two for the Notariato policy even if only a few provisions affect the security of the policy, which usually lies between level 3 and 4. In the context of cross certification the right choice should be level 3 , even if some little adjustments on the policy could be applied. These results can be adopted in two ways:
7 ConclusionsIn this paper we have presented a technique that helps security administrator to analyze, compare and classify in terms of security levels security policies. The proposed technique is able to evaluate the policies by means of a fuzzy aggregation model, in order to take into account both technical and nontechnical provisions. The fuzzy evaluation method is the basis for the building of a reference model to classify and analyze policies. The technique is based on the following steps:
Page 172 We have shown how to formalize the policies (section 3), how to evaluate them using the fuzzy technique (section 4) and how to build the REM (section 5), verifying that the evaluation method gives us valid results using the Canadian Polices as reference. Finally we have applied the technique on a case study (section 6): a real certificate policy that comes from a legally recognized CA (Notariato Italiano ) which works in a country with a different legislation compared to the one that defines the security levels. In conclusion we have shown that our analysis helps the administrator to understand which is the best way to improve a policy and helps the involved CAs to understand how to perform Cross Certification. An interesting result is that the rigorous classification of the Notariato policy in terms of the Canadian rules will lead to an underestimated security level, but, with our technique we are able to point out that just a little improvement on some provisions of the Notariato policy, increases the security level. References[Bellman, 1970] R. E. Bellman, L. A. Zadeh, "Decision making in a fuzzy environment"; Management Science, 17, 4, 141164, 1970. [Calvo, 2002] T. Calvo, G. Mayor, R. Mesiar, "Aggregation Operators"; PhysicaVerlag, New York, 2002. [Canada Government, 1999] "Digital Signature and Confidentiality, Certificate Policies for the Government of Canada Public Key Infrastructure"; version 3.02, 1999. [Canfora, 2001] G. Canfora, L. Troiano,"An Extensive Comparison between OWA and OFNWA Aggregation"; Proc. VIII Sigef Congress, Naples, Italy, 2001. [Canfora, 2002] G. Canfora, L. Troiano, "The Importance of Dealing with Uncertainty in the Evaluation of Software Engineering Methods and Tools"; Proc. SEKE'02, ACM Publishing, Ischia, Italy , 691698, 2002. [Canfora, 2003a] G. Canfora, L. Troiano, "A rulebased model to aggregate criteria with different relevance"; Proc. IFSA'03, LNCS, SpringerVerlag Publishing, Istanbul, Turkey , 311318, 2003. [Canfora, 2003b] G. Canfora, L. Cerulo, R. Preziosi, L. Troiano, "A tool for Decision Support implementing OFNWA approach: a case study"; Proc. SEKE'03, The Knowledge System Institute Publishing, San Francisco Bay, USA , 714720, 2003. [Casola, 2002] V. Casola, A. Mazzeo, N. Mazzocca, V. Vittorini, "Policy Formalization to combine separate systems into larger connectednet works of trust"; Proc. NetCon'02, Paris, France, 2002. [Casola, 2003] V. Casola, A. Mazzeo, N. Mazzocca, V. Vittorini, "Policy based interoperability in distributed security infrastructures"; Proc. of Concurrent Engineering: Enhanced Interoperable Systems, Madeira, Spain, 2003. Page 173 [Casola, 2004] V. Casola, "A Policy Based Methodology for the Analysis, Modelling and Implementation of Security Infrastructures". PhD thesis, Seconda Universit?a di Napoli, Scuola di Dottorato in ingegneria elettronica, 2004. [Chokhani, 1999] S. Chokhani, W. Ford, RFC 3647: Internet X.509 Public Key Infrastructure Certificate Policy and Certification Practices Framework, 1999. [Curry, 2000] I. Curry, "Trusted PublicKey Infrastructures"; version 1.2, Entrust Technologies, www.entrust.com, 2000. [Damianou, 2001] N. Damianou,N. Dulay, , E.C. Lupu, M. S. Sloman, "The Ponder Policy Specification Language"; Proc. Policy'01, Bristol, UK., 2001. [Ford, 1997] W. Ford, M.S. Baum, "Secure Electronic Commerce"; Prentice Hall Inc., Upper Saddle River, 1997. [Grill, 2000] S. Grill, "An approach to formally compare and query Certification Prac tice Statements", Informatik GI Workshop, Berlin, 2000. [Hosmer, 1992] H. H. Hosmer, "Using fuzzy logic to represent security policies in the multipolicy paradigm"; ACM SIGSAC Review, 10, 4 , 1221, 1992. [Housley, 1999] R. Housley, W. Ford, W. Polk, D. Solo, RFC 2459: Internet X.509 Public Key Infrastructure Certificate and CRL Profile, 1999. [Jajodia, 1997] S. Jajodia, P. Samarati, V. S. Subrahmanian, "A Logical Language for Expressing Authorizations"; Proc. IEEE Symposium on Security and Privacy, Oakland,USA, 1997. [Klir, 1995] G. J. Klir, B.Yuan, "Fuzzy Sets and Fuzzy Logic: Theory and Applications"; Prentice Hall, Englewood Cliffs, NJ, 1995. [Klobucar, 1999] T. Klobucar,B. JermanBlazic, "A Formalization and evaluation of certificate policies"; Computer Communication 22 , 11041110, 1999. [Lupu, 1999] E.C. Lupu, M.S. Sloman, "Conflicts in PolicyBased Distributed Systems Management"; IEEE Transactions on Software Engineering Special Issue on Inconsistency Management, 25, 852869, 1999. [Mendes, 1995] S. Mendes, C. Huitema,"A new approach to the X.509 framework: allowing a global authentication infrastructure without a global trust model"; IEEE Proceedings of the 1995 Symposium on Network and Distributed System Security (SNDSS'95), 172189, 1995. [Notariato Italiano, 2002] "Manuale Operativo del Consiglio Nazionale del Notariato"; September 2002. Italian Policy for Digital Signature registered inthe public registry of Certification Authorities, hold by CNIPA, 2002. [NIST, 2001] NIST 2001, Report of Federal Bridge Certification Authority Initiative and Demonstration. [Turnbull, 2000] J. Turnbull, CrossCertification and PKI Policy Networking. Version 1.1, Entrust Technologies, www.entrust.com. 2000. [Yager, 1988] R.R. Yager, "On ordered weighted averaging aggregation operators in multicriteria decision making"; IEEE Trans. on Systems, Man, and Cybernetics, 18, 1, 183190, 1988. [Yager, 1993] R.R. Yager, "Families of OWA operators"; Fuzzy Sets and Systems, 59, 125148, 1993. [Zadeh, 1965] L.A. Zadeh, "Fuzzysets"; Information and Control 8, 3, (1965), 338353. [Zadeh, 1972] L.A. Zadeh, "A fuzzysettheoretic interpretation of linguistic hedges"; Journal of Cybernetics, 2, 3, 4&sh;34, 1972. Page 174 |
|||||||||||||||||
 wiap(i)
(2)
wiap(i)
(2)  [0,1] and are such that
[0,1] and are such that  ) defined as:
) defined as: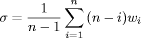 (4)
(4)  = 0 we get
= 0 we get  = 0 we get
= 0 we get 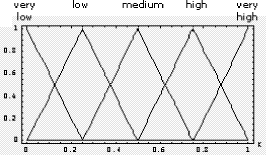
 xL1
xL1
 xL2
xL2