| Submission Procedure |
A Packing Problem, Solved by Genetic AlgorithmsGeorg Franck-Oberaspach Dietmar B. Schweiger Institut für Theoretische Physik,
University of Technology Vienna K. Svozil Institut für Theoretische Physik, University
of Technology Vienna Abstract: An arbitrary number of points are arranged in a given twodimensional simply connected region such that their mutual distances and the distance from the region boundary becomes a maximum. 1 Genetic algorithms as optimization tool for packing problemsWe report the solution of twodimensional packing problems by the method of genetic algorithms. Thereby, we do not seek a configuration which minimizes the space necessary to arrange rigid objects, but rather we attempt to maximize the space available to any single object. Problems of this kind appear in as diverse research areas as physical potential theory as well as in architectural urban planning strategies. Genetic algorithms [1, 2, 3, 4, 5] represent an optimization method for computationally "hard" problems [6, 7, 8]. A "genetic pool" of solutions to a given problem is transformed by random "mutations" and "crossovers" of their respective codes. The new solutions are then evaluated by a " fitness function," such that only the best solutions "survive." This procedure can be applied until the "pool" of solution reaches a (statistical) fixed point. Although there is no effective guarantee to find (one of) the optimal solution(s), for many applications the method converges quite fast and to a reasonable result. To be more specific, consider an arbitrary number of n dimensionless objects. Assume further an arbitrary closed polygon with m edges defining a simply connected twodimensional region. Every single possible solution s is encoded by the concatenation of the x; y-coordinate pair of each object; i.e., s = {x1 , y1 , x2 , y2 , ..., xn ; yn}: Page 464 The fitness function can be written as the sum of contributions from the mutual distances between objects, as well as between the objects and the edges; i.e.,
where
and
stand for the number of point-distances and the number of line-distances,
respectively. The effective potential is encoded by the function g.
Its exact form is problem specific. In the examples presented below potentials
of the form g(d) The proposed genetic algorithm is many-character based and the mutation- and crossover operator work as usual with the only exception that after a crossover the individuals with the lowest fitness are replaced by the offspring instead of the parents. Its formulas are the result of several attempts to solve this problem, trying different kind of genetic algorithms (e.g., binary based, many character based) and different kind of fitness functions. One underlying concept was the simulation of the behavior of point charges that move freely on a polygon shaped area, whereby in terms of electrostatic potentials, the edges carry "repelling charge" as well. The "electrostatical potential" of the arrangement should become a minimum, thereby satisfying the requirement to maximize the space available for any single object ("point charge") in accord with all others. This should be comparable to "low potential states" in electrostatics. 2 Example configurationsWe shall mention a few examples next. The first nontrivial configuration is to distribute seven points on the square, as depicted in Figure 1. (The outcomes of simulations with four to six points are not listed, because, as can be expected, four points were always on the edges, the fifth remaining in the center.) Typical outcomes are shown in Figure 2. Small changes of the initial configuration always result in small differences of the computed optimum, because the fitness values of the arrangements do not differ strong enough such that the genetic algorithm cannot converge to a single distribution. Page 465
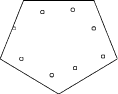
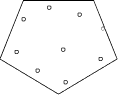
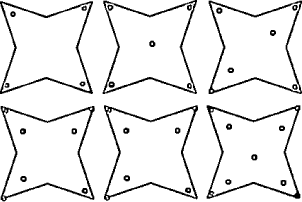
Next a pentagon-shaped area is considered, thereby increasing the number of points successively from five to nine. At five points each object is near a corner as expected; cf. Figure 3. At six to eight points, the arrangement is in a kind of circle along the edges. The example with eight points is shown in Figure 4. As the number of points increases, the fitness function causes the points move nearer to the edges. For nine points, one of them is placed in the center; cf. Figure 5. We now consider star-shaped areas. The star is a very illustrative shape because it is quite obvious where to place the points in the special case of four of them. This con figuration is drawn in the first picture of Figure 6. Four objects packed in a four-folded star. It is interesting that the points are forced to appear very near at the lines that form the corners. This trend continues and is getting more extreme as we raise the number successively up to nine. Normally this behavior should be prevented by the -1/d proportional potential function, but this seems to be compensated by the large number of point and line distances which are increased in this case. Page 466
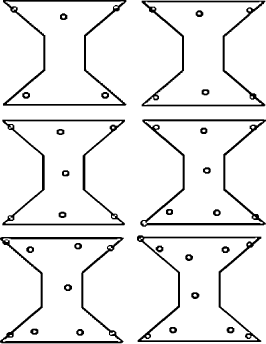
Finally Figure 7 depicts a study of five to ten points on a "hourglass"-shaped region, respectively. 3 ConclusionThese and further investigations indicate that the method of genetic algorithms is quite useful in the implementation of packing problems of the considered sort. Thereby, the mayor advantages of genetic algorithms - the fast convergence and the ability of the solution to escape a local minimum/maximum via mutation - could be clearly demonstrated. Page 467
Figure 6: Four to nine objects packed in a four-folded star. Page 468
Page 469 References[1] John. H. Holland. Adaption in Natural and Articial Systems. MIT Press, Cambridge, MA, 1992. [2] John. H. Holland. Hidden Order. Addison Wesley, Reading, MA, 1995. [3] David E. Goldberg. Genetic Algorithms in Search, Optimization & Machine Learning. Addison Wesley, Reading, MA, 1989. [4] John. H. Holland. Genetic algorithms. Scientic American, 267(7):44-50, July 1992. [5] Melany Mitchell. An Introduction to Genetic Algorithms. MIT Press, Cambridge, MA, 1996. [6] M. R. Garey and D. S. Johnson. Computers and Intractability. A Guide to the Theory of NP-Completeness. Freeman, San Francisco, 1979. [7] J. E. Hopcroft and J. D. Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley, Reading, MA, 1979. [8] Cristian Calude. Theories of Computational Complexity. North-Holland, Amsterdam, 1988. Page 470 |
|||||||||||||||||
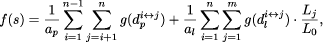
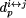 stands for the distance between point i and point j,
stands for the distance between point i and point j, 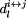 represents a distance between point i and line j, and the
factor L j / L0 has been introduced
to weight the contribution of edges of different lengths: Lj
is the length of edge j, and L0 is length of the
shortest edge of the polygon. The potential is encoded by the function
g. The normalization factors
represents a distance between point i and line j, and the
factor L j / L0 has been introduced
to weight the contribution of edges of different lengths: Lj
is the length of edge j, and L0 is length of the
shortest edge of the polygon. The potential is encoded by the function
g. The normalization factors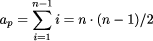
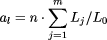
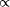 - 1/d have been considered. The resulting
code is quite efficient and yields good results for problems which are
exactly solvable.
- 1/d have been considered. The resulting
code is quite efficient and yields good results for problems which are
exactly solvable.