| Submission Procedure |
Group Theoretical Aspects of Reversible Logic Gates(Vakgroep zuivere wiskunde en computeralgebra, Universiteit Gent, Belgium Galglaan 2, B - 9000 Gent ls@cage.rug.ac.be) Alexis De Vos
Gerald Jacobs
Abstract: Logic gates with three input bits and three output bits have a privileged position within fundamental computer science: they are a sufficient building block for constructing arbitrary reversible boolean networks and therefore are the key to reversible digital computers. Such computers can, in principle, operate without heat production. As there exist as many as 8! = 40,320 different 3-bit reversible truth tables, the question arises as to which ones to choose as building blocks. Because these gates form a group with respect to the operation `cascading', we can apply group theoretical tools, in order to make such a choice. Key Words: reversible computing, group theory, permutations Category: B.6.1 1 IntroductionConventional computers are built from basic building blocks, such as the AND, NAND, OR, NOR, and XOR gates. See Table 1. Such tables are logically irreversible. This means that, if we forget the value of the input (A, B), knowledge of the output P is not sufficient to calculate backwards and to recover the value of (A, B).According to Landauer's principle [1] [2] [14] [15] [18], logic computations that are not reversible, necessarily generate heat, i.e. kTlog(2), for every bit of information that is lost. Here k is Boltzmann's constant and T the temperature. For T equal room temperature, this package of heat is small, i.e. 2.9 x 10 -21 joule, but non-negligible. In order to produce zero heat, a computer is only allowed to perform reversible computations. Such a logically reversible computation can be `undone': the value of the output suffices to recover what the value of the input `has been'. The hardware of such a reversible computer cannot be constructed from the conventional gates of Table 1. On the contrary, it consists exclusively Page 307
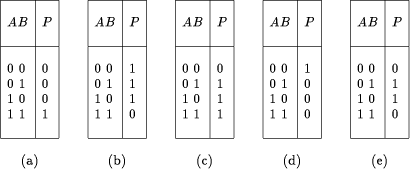
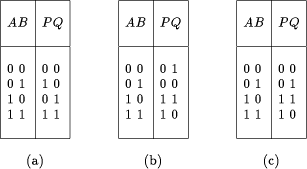
Table 1: Classical truth tables: (a) AND , (b) NAND , (c) OR , (d) NOR , (e) XOR.
of logically reversible building blocks. The number of output bits of a reversible logic gate necessarily equals its number of input bits. We will call this number the `logic width' of the gate. Fredkin and Toffoli [10] [19] have demonstrated that three inputs and three outputs is necessary and sufficient in order to construct a reversible implementation of an arbitrary boolean function of a finite number of logic variables. Thus, from the fundamental point of view, reversible logic gates with a width equal to three have a privileged position. The truth table of a logic gate of width w consists of 2w lines, each containing two w-bit numbers: the w-bit input (A, B, C, ...) and the w-bit output (P, Q, R, ...). For convenience, all possible inputs, ranging from (0, 0, 0, ...) to (1, 1, 1, ...), are ordered arithmetically. Such a gate is reversible if-and-only-if all 2w output numbers form a permutation of the 2w input numbers. Hence, there exist exactly (2w )! different reversible gates of width w. In particular, there are 8! = 40,320 reversible gates with 3-bit width. The present paper investigates which of these 40,320 gates fulfil the role of universal building block, and which fulfil this job more efficiently than the others. In order to tackle the problem, we will successively study the reversible gates with w = 1, w = 2, and w = 3. 2 Calculation with a single bitThere exist only four different truth tables with one bit input and one bit output. Two of them are logically irreversible: the resetter (P = 0) and the setter (P = 1). The two others are reversible: the follower (P = A) and the inverter (P = NOT A). If, for example, we have `forgotten' the value of A, knowledge of the value of the inverter's output P suffices to recover it.Note that among the 1-bit reversible gates, the NOT gate is a `generator'. This means we can make any reversible gate of width 1 by combining a finite number of this particular gate. Indeed, a follower can be fabricated by the sequence of two inverters. The opposite is not true: one cannot fabricate an inverter by cascading followers. Page 308
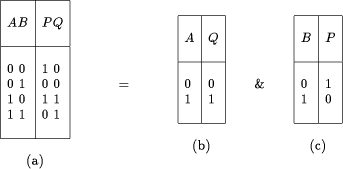
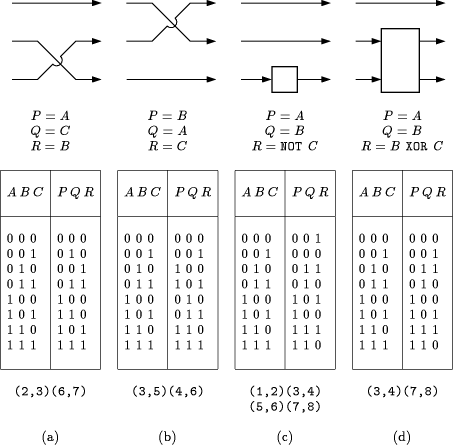
3 Calculation with two bitsThere are 44 = 256 different truth tables with two inputs (A, B) and two outputs (P, Q). Among them, only 4! = 24 are reversible. However, some of these twenty-four truth tables fall apart into two separate 1-bit reversible tables. E.g. Table 2a decomposes into one follower Q = A (Table 2b) and one inverter P = NOT B (Table 2c). On the contrary, truth Table 3b is an example of a 2-bit reversible table that cannot be reduced to two separate 1-bit reversible tables, and therefore is called a true two-bit reversible gate. Among the 24 reversible 2-bit tables, only 16 are true 2-bit tables.Table 2: Falling apart of a truth table.
All reversible true 2-bit gates can be fabricated from the same building
block, combined with an inverter before and/or an inverter after. Indeed,
Table 3b together with the inverter (Table 3a) forms a set of two building
blocks with which we can synthetize an arbitrary reversible 2-bit gate.
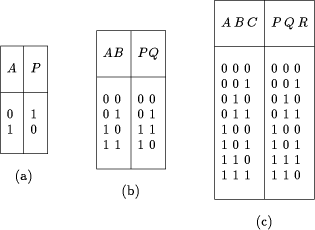
Truth Table 3b is called the CONTROLLED NOT by Feynman [8]
[9]. Its logic operation looks like this:
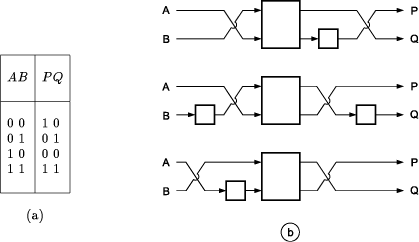
where XOR is the abbreviation of the EXCLUSIVE OR function. The gate is the reversible form of the classical (irreversible) XOR gate. The latter is represented in Table 1e. Figure 1 gives a representative example of a 2-bit reversible gate,
realized by combining NOT and CONTROLLED NOT gates. Whereas
output Q simply equals input B,
output P can be described in three different ways:
Page 309
Table 3: Feynman's truth tables: (a) NOT, (b) CONTROLLED NOT, (c) CONTROLLED CONTROLLED NOT.
These three boolean expressions are identical, but lead to different physical realizations. We note, however, that these implementations not only make use of the 1-bit NOT function and the 2-bit CONTROLLED NOT function, but also of the 2-bit exchanger, i.e. the gate that interchanges two logic variables (realizing P = B as well as Q = A). This is an example of a general property: the EXCHANGER, the NOT, and the CONTROLLED NOT form a natural `generating set' for the twenty-four 2-bit reversible gates. More precisely, each reversible 2-bit gate can be synthetized by taking one or zero CONTROLLED NOTs and adding one or zero EXCHANGERs and one or zero NOTs to the left and to the right of it. Note that neither the EXCHANGER nor the NOT is a true 2-bit gate, but the CONTROLLED NOT is one. See Table 4. 4 Calculation with three bitsThere exist 88 = 16,777,216 different truth tables with 3 inputs and 3 outputs. Among them, only 8! = 40,320 are reversible. However, 48 of these truth tables fall apart into three separate 1-bit reversible tables and another 288 fall apart into one 1-bit and one (true) 2-bit reversible gate. Thus, among the 40,320 reversible 3-bit gates, only 39,984 are true 3-bit gates.Two notorious examples are the Fredkin gate [10] [19] and Feynman's CONTROLLED CONTROLLED NOT gate [8] [9]. The truth table of the latter is given in Table 3c. The former is shown in Table 5a. Both have a particular property: each is a universal primitive. This means that any boolean function of any finite number of logic input variables can be implemented by combining a finite number of such building blocks. The proof consists of two steps [19]: one first proves that the building block suffices to implement the NAND function (Table 1b), then one refers to the fact that the NAND function is a universal primitive. The latter Page 310
Figure 1: The synthesis of a 2-bit reversible gate: (a) truth table, (b) three different implementations combining NOTs and CONTROLLED NOT. Table 4: The three generators of the 2-bit reversible gates: (a) EXCHANGER, (b) NOT, (c) CONTROLLED NOT.
step is a well-known theorem. The former step is demonstrated by introducing a so-called preset: we keep one or two inputs fixed and look how the three outputs are function of the remaining input(s). Among the 39,984 reversible true 3-bit gates, many have the universality property. It is clear, however, that the number 39,984 is too large to allow `manual' inspection. We have to recur to computer-algebra software specially dedicated to group theory, such as GAP [11] [17] and Magma [3] [12]. In the present study, we have chosen the GAP approach, because of GAP's built-in commands DoubleCoset and DoubleCosets. Page 311
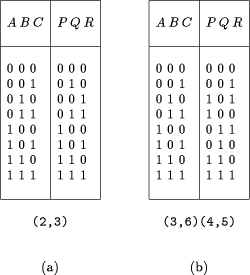
Table 5: Truth tables: (a) Fredkin's conservative gate, (b) a `pseudo-inverting' gate.
5 Groups and subgroupsBecause of the universality property of some of the 3-bit reversible gates, we now continue the w = 3 case in more detail.When a reversible 3-bit gate x is cascaded by a reversible 3-bit gate y (i.e. when the P output of gate x is connected to the A input of y, etc.), then a new reversible 3-bit gate is formed, denoted xy. The 40,320 reversible truth tables of width 3 therefore form a group [16], say R, which is isomorphic to the symmetric group S8 . The identity element of the group is the 3-bit follower (P = A, Q = B, and R = C). In GAP, each element of R is denoted by its permutation notation. E.g. the follower is denoted (), whereas the CONTROLLED CONTROLLED NOT is written (7,8), because the seventh and the eighth line of the truth table (i.e. Table 3c) are interchanged. In order to classify the large number of elements of the group R, we will introduce in the following paragraphs three different important subgroups, namely E with 6 elements, F with 48 elements, and finally G with 1,344 elements. They are ordered as E < F < G < R where < denotes `is proper subgroup of'. By means of each of these three subgroups, we will partition R into double cosets, which will serve as equivalence classes in the application of Section 6. An important subgroup of R is formed by the follower together with the five elements representing mere relabellings. Table 6a shows the example e1, satisfying P = A, Q = C, and R = B, i.e. performing an exchange of B and C. In Page 312
permutation notation, gate e1 is written (2,3)(6,7). A second example is e2 or (3,5)(4,6). See Table 6b. Together these two elements generate the whole subgroup of exchangers. The importance of this subgroup E comes from the fact that these gates are trivial to implement in any technology. E.g. in electronics, they consist merely of cross-overs of metal lines. The subgroup E of exchange gates contains six elements. It is denoted G6 (SW) by Rayner and Newman [16] and is isomorphic to the symmetric group S3 . Results from GAP show us that E partitions the full group R into 1,172 distinct double cosets. A double coset of an element g consists of all elements e´ ge´´ , where both e´ and e´´ are elements of the subgroup E. This means that, although there exist 40,320 different reversible gates, there are only 1,172 `really different' ones, as soon as we consider exchangers as `for free'. From these 1,172 gates, all other 39,148 gates can be fabricated by merely adding one relabelling gate to the left and one to the right. In a next step, we can enlarge the above subgroup E, by introducing the inverter or NOT gate. One can either invert A (i.e. realize the gate P = NOT A, Q = B, and R = C), or invert B (i.e. realize P = A, Q = NOT B , and R = C), or invert C (P = A, Q = B, and R = NOT C ). As an example, the cycle notation of the last gate is (1,2)(3,4)(5,6)(7,8). These three inverters (denoted i1, i2 , and i3 ) generate a subgroup of order 23= 8, isomorphic to Z23, where Z2 is the cyclic group of order 2. Together, the subgroup E of exchangers and the subgroup I of inverters generate a new subgroup F of order 48, isomorphic to S3:Z23, the semi-direct product of S3 and Z23. The elements of F are exactly the 48 gates mentioned in Section 4, i.e. the 3-bit gates that fall apart into three distinct 1-bit gates. Using GAP, we find that the subgroup F partitions the full group R into 52 distinct double cosets. This means that, although there exist 40,320 different reversible gates, there are only 52 `really different' ones, if we consider both exchangers and inverters as `for free'. From these 52 gates, corresponding to representatives of the 52 distinct double cosets of F, all other 40,268 gates can be fabricated by merely adding one free gate to the left and one to the right. Table 7 gives a list of all 52 double cosets ki . Note that GAP gives them in a specific order, which has no a priori meaning for the user. We also get a representative ri of class ki. Again GAP's way of choosing this representative is not transparent to the user. The different double cosets constructed with F sometimes have different size. Table 7 gives ni , i.e. the number of elements in the double coset. At first sight, it may be a surprise that a double coset may contain less than 482 = 2,304 members. This is caused by the fact that different products f´gf´´ (with g a member of R and both f´ and f´´ members of F) can lead to equal results. It is possible to prove that each double coset contains a number of elements which is a multiple of 48. Double coset k1 is the subgroup F itself, with the follower () as representative r1 . We remark that Feynman's gate (7,8) is the representative r4 of class k4 . If we take the elements of subgroup F and add the representative ri of ki , then these 49 elements together generate a subgroup. Such a subgroup is called the closure of F and ri . Its order we denote by mi in Table 7. From GAP, we learn that
Page 313 separated by merely exchangers and/or inverters. In this case, we call ri universal.
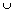 k8 k8 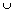 k31 k31 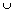 k40 k40
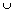 k49 is the closure of subgroup F and the subgroup of
the 36 conservative gates. A conservative gate [10]
is a gate where the output (P, Q, R) always has the same number
of 1's as the input (A, B, C). Fredkin's gate (2,3) is
an example. The subgroup
k1 k49 is the closure of subgroup F and the subgroup of
the 36 conservative gates. A conservative gate [10]
is a gate where the output (P, Q, R) always has the same number
of 1's as the input (A, B, C). Fredkin's gate (2,3) is
an example. The subgroup
k1 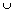 k2 k2 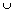 k3
is the closure of F and the subgroup of the 16 pseudo-inverting
gates. We call a `pseudo-inverting' gate a gate where the output (P, Q, R) always is equal to either the input (A, B, C) or to
(NOT A, NOT B, NOT C). Its
permutation notation consists merely of transpositions (i,9-i).
Table 5b shows an example. The meaning of the subgroup
k1
k3
is the closure of F and the subgroup of the 16 pseudo-inverting
gates. We call a `pseudo-inverting' gate a gate where the output (P, Q, R) always is equal to either the input (A, B, C) or to
(NOT A, NOT B, NOT C). Its
permutation notation consists merely of transpositions (i,9-i).
Table 5b shows an example. The meaning of the subgroup
k1 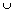 k3 k3
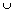 k19 k19 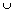 k21 k21 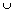 k31 k31
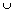 k33 k33 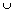 k34 will become clear below. k34 will become clear below.
In a final step, we can enlarge subgroup F, by adding a Feynman CONTROLLED NOT. See Table 6d. The resulting G is a subgroup of R and a supergroup of F. It is isomorphic to 23:L3 (2), the semi-direct product of 23, i.e. the additive group of all binary vectors of length 3, and L3(2), i.e. the multiplicative group of all non-singular binary 3 x 3 matrices. In detail, G is isomorphic to the multiplicative group of all non-singular binary 4 x 4 matrices of the form
with det(A) Page 314
identical to the subgroup k1
Page 315
Page 316
Page 317
6 ApplicationWhich of R's three subgroups (E, F, or G) is of importance, depends on the technological circumstances. In almost each technology the exchangers are `for free'. E.g. in electronics, they are implemented by a mere metal cross-over. In the special case of dual-line electronics, each logic variable is represented by two metal lines of opposite logic value, e.g. A together with NOT A. Therefore, in dual-rail electronics, also an inverter is `free of charge': we only need a metal cross-over to exchange A with NOT A. In this technology, the CONTROLLED NOT is not for free. Thus we are in the case of the free subgroup F [5] [6] [7].The following question arises [13]. We like to be able to synthetize any arbitrary member of R with the help of a limited number of generators. In electronics, we say: we like to implement any arbitrary reversible 3-bit gate with the help of a library with a limited number of standard cells. If we denote by s1, s2, ..., sm the different members of the library, then an arbitrary member r of R must satisfy r = f ´s´f´´s´´f´´´...s (n) f (n+1), (1) where s´, s´´, ..., s (n) are elements of the library {s1, s2 , ..., sm} and f´, f´´, f ´´´, ..., f(n+1) are elements of F = {f1, f2, ..., f48}. The number n is called the `logic depth' of the implementation. In order to minimize the number of standard cells, we have to choose them from different double cosets and not from double coset k1 . Thus the library will be a subset of the representatives r2, r3, ..., r52. From Table 7, it follows that a library with a single building block is sufficient: each of the representatives r4, r6, r10, r12, r14, r16, r17, r20, r22, r24, r26, r27, r29, r30, r 32, r35, r37, r39, r42, r44, r47, r51 and r52 have mi = 40,320 and are thus sufficient to generate the whole group R. But, these 23 solutions are not Page 318
equivalent. Indeed, we not only want to limit the number p of different
building blocks in the library, we also like to limit the number of times
we have to use the blocks, i.e. we like to minimize the depth n
of the products (1). It turns out that with building block r14
all elements of R can be synthetized with n None of the double cosets k14, k44
, and k47 appears in the lattice of Figure
2, except at the top, in the parent group R itself. Indeed,
any element of any subgroup of Figure 2 can only generate
other elements of that particular subgroup. The underlying reason is clear:
such elements show `too much symmetry'. E.g. conservative gates (such as
Fredkin's gate) can, by cascading, only generate elements of k1 If we consider depth n = 4 as too deep a cascade (too much silicon
surface area), we can construct a larger library. If we choose an p
= 2 library, there are four equivalent optimal combinations: r14
together with r18, r14 together with
r41,
r44
together with r48 , and r44 together
with r50 . Now we have n
7 ConclusionThe reversible gates of width w form a group, isomorphic to the symmetric group S2w . Group theory in general, and double cosets in particular, are wellPage 319
suited to detect different classes within the (2w )! elements of the group. This can lead to an optimized choice of a set of generators. In electronics, this means an optimal set of hardware building blocks. With the help of GAP, we identified optimal gates g that are able to generate all other elements of R by means of a product of the form f´ gf´´gf´´´ ... of minimal length. Acknowledgement Leo Storme is research associate of the Fund for Scientific Research - Flanders (Belgium). Page 320 References[1] Bennett, C.: "Logical reversibility of computation"; I.B.M. Journal of Research and Development 17 (1973), 525-532.[2] Bennett, C., Landauer, R.: "The fundamental physical limits of computation"; Scientific American 253 (July 1985), 38-46. [3] Bosma, W., Cannon, J., Playoust, C.: "The Magma Algebra System I: the user language"; Journal of Symbolic Computation 3-4 (1997), 235-265. [4] Conway, J.H., Curtis, R.T., Norton, S.P., Parker, R.A., Wilson, R.A.: "Atlas of finite groups"; Oxford University Press, New York (1985), p. 22. [5] De Vos, A.: "Introduction to r-MOS systems"; Proc. 4 th Workshop on Physics and Computation, Boston (1996), 92-96. [6] De Vos, A.: "Towards reversible digital computers"; Proc. European Conference on Circuit Theory and Design, Budapest (1997), 923-931. [7] De Vos, A.: "Reversible computing"; Progress in Quantum Electronics 23 (1999), 1-49. [8] Feynman, R.: "Quantum mechanical computers"; Optics News 11 (1985), 11-20. [9] Feynman, R.: "Feynman lectures on computation" (A. Hey and R. Allen, eds); Addison-Wesley, Reading (1996). [10] Fredkin, E., Toffoli, T.: "Conservative logic"; International Journal of Theoretical Physics 21 (1982), 219-253. [11] http://www.can.nl/SystemsOverview/Special/GroupTheory/GAP/index.html [12] http://www.maths.usyd.edu.au:8000/u/magma/index.html [13] Jacobs, G.: "Algebra der reversibele logische schakelingen"; M.Sc. thesis, Universiteit Gent, Gent (1998). [14] Keyes, R., Landauer, R.: "Minimal energy dissipation in logic"; I.B.M. Journal of Research and Development 14 (1970), 153-157. [15] Landauer, R.: "Irreversibility and heat generation in the computational process"; I.B.M. Journal of Research and Development 5 (1961), 183-191. [16] Rayner, M., Newman, D.: "On the symmetry of logic"; Journal of Physics A: Mathematical and General 28 (1995), 5623-5631. [17] Schönert, M.: "GAP"; Computer Algebra Nederland Nieuwsbrief 9 (1992), 19-28. [18] Stix, G.: "Riding the back of electrons"; Scientific American 279 (September 1998), 20-21. [19] Toffoli, T.: "Reversible computing"; in: "Automata, languages and programming" (J. De Bakker and J. Van Leeuwen, eds); Springer, New York (1980), pp. 632-644. Page 321 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
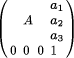
 0 and with a1, a2, a3
0 and with a1, a2, a3  {0,1}. See Reference [
{0,1}. See Reference [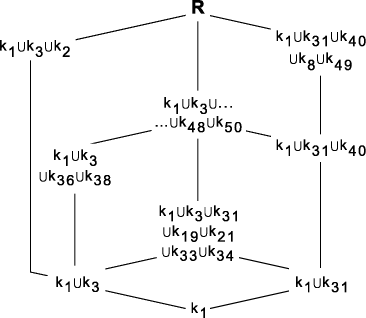

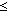 4. The elements of k1 need no r14 block
(i.e. n = 0); the elements of k14 need only one
r14
block (i.e. n = 1); most elements of R need n = 2
or n = 3; only the elements of k34 need four cascaded
r14
blocks (n = 4); on the average an arbitrary class of R needs
32/13 = 2.46 building blocks in cascade. Exactly the same results apply
to the building block r44 and to r47
.
4. The elements of k1 need no r14 block
(i.e. n = 0); the elements of k14 need only one
r14
block (i.e. n = 1); most elements of R need n = 2
or n = 3; only the elements of k34 need four cascaded
r14
blocks (n = 4); on the average an arbitrary class of R needs
32/13 = 2.46 building blocks in cascade. Exactly the same results apply
to the building block r44 and to r47
.