|
Invariance Properties of Random Sequences
Peter Hertling (Department of Computer Science, The University of Auckland, New Zealand)
Yongge Wang (Department of Computer Science, The University of Auckland, New Zealand)
Abstract: We present invariance characterizations of different types of random sequences. We correct Schnorr's original, incorrect characterization of Martin-Loef ran dom sequences, compare it with Schnorr s corresponding characterization of his own randomness concept, and give a similar, new characterization of Kurtz random sequences. That is, we show that an infinite sequence 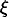 is Kurtz random if and only if for every partial, computable, measure-invariant function is Kurtz random if and only if for every partial, computable, measure-invariant function 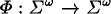 the sequence the sequence 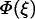 is not recursive. is not recursive.
1.) Proceedings of the First Japan-New Zealand Workshop on Logic in Computer Science, special issue editors D.S. Bridges, C.S. Calude, M.J. Dinneen and B. Khoussainov.
Keywords: Randomness, invariance properties
Categories: F.1
|