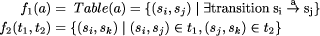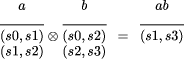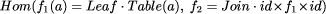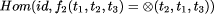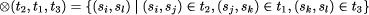| Submission Procedure |
Structured Parallel Computation in Structured DocumentsD.B. Skillicorn Abstract: Document archives contain large amounts of data to which sophisticated queries are applied. The size of archives and the complexity of evaluating queries makes the use of parallelism attractive. The use of semantically-based markup such as SGML makes it possible to represent documents and document archives as data types. We present a theory of trees and tree homomorphisms, modelling structured text archives and operations on them, from which it can be seen that: many apparently unrelated tree operations are homomorphisms; homomorphisms can be described in a simple parameterised way that gives standard sequential and parallel implementations for them; and certain special classes of homomorphisms have parallel implementations of practical importance. In particular, we develop an algorithm for path expression search, a novel powerful query facility for structured text, taking time logarithmic in the text size. This algorithm is the first example of a new algorithm discovered using homomorphic skeletons over data types. Keywords: structured text, categorical data type, software development methodology, parallel algorithms, query evaluation. Category: D.1.3 Concurrent Programming - Parallel Programming; D.2.2 Tools and Techniques; D.3.3 Language Constructs and Features; H.2.3 Languages - Query Languages; H.3.3 Information Search and Retrieval; I.7.2 Document Preparation. 1 Structured Parallel ComputationComputations on structured documents are a natural application domain for parallel processing. This is partly because of the sheer size of the data involved. Document archives contain terabytes of data, and analysis of this data often requires examining large parts of it. Also, advances in parallel computer design have made it possible to build systems in which each processor has sizeable storage associated with it, and which are therefore ideal hosts for document archives. Such machines will become common in the next decade. The use of parallelism has been suggested for document applications for some time. Some of the drawbacks have been pointed out by Stone [Sto87] and Salton and Buckley [SB88] - these centre around the need of most parallel applications to examine the entire text database where sequential algorithms examine only a small portion, and the consequent performance degradation in accessing secondary storage. While this point is important, it has been to some extent overtaken by developments in parallel computer architecture, particularly the storage of data in disk arrays, with some disk storage local to each processor. As we shall show, the use of parallelism allows such an increase in the power of query operations that it will be useful even if performance is not significantly increased. Parallel computation is difficult in any application domain for the following reasons: Page 42 - There are many degrees of freedom in the design space of the software, because partitioning computations among processors strongly influences communication and synchronisation patterns, which in turn have a strong effect on performance. Hence finding good algorithms requires extensive search in the absence of other information; - Parallelism in an algorithm is only useful if it can be harnessed by some available parallel architectures, and harnessed in an efficient way; - Expressing algorithms in a way that is abstract enough to survive the replacement of underlying parallel hardware every few years is difficult; - It is hard to predict the performance of software on parallel machines without actually developing and executing it. The extensive use of semantically-based markup, and particularly the use of SGML [ISO86], means that most documents have a de facto tree structure. This makes it possible to model them by a data type with enough formality that useful theory can be applied. We will use the theory of categorical data types [Ski94], a particular approach to initiality, emphasising its ability to hide those aspects of a computation that are most difficult in a parallel setting. Operations on structured text are expressed as homomorphic skeletons, homomorphisms on data types. As usual in parallel computation, the use of structure improves both the clarity of algorithm description and the ease of designing implementations. Categorical data types generalise abstract data types by encapsulating not only representation of the type, but also the implementation of homomorphisms on it. This approach was pioneered by Bird and Meertens [Bir87] and its use for software development by transformation has come to be known as the Bird-Meertens Formalism. In object-oriented terms, the only methods available on constructed types are homomorphisms. As a parallel programming model this is ideal, since the partitioning of the data objects across processors, and the communication patterns required to evaluate homomorphisms can remain invisible to programmers. Programs can be written as compositions of homomorphisms without any necessary awareness that the implementations of these homomorphisms might contain substantial parallelism. Recall that a homomorphism is a function that respects the structure
of its arguments. If an argument object is a member of a data type with
constructor h(a This equation describes two different ways of computing the result of
applying h to the argument a There are two things to note about the computation strategy implied
by the right hand side. The first is that it is recursive. If b
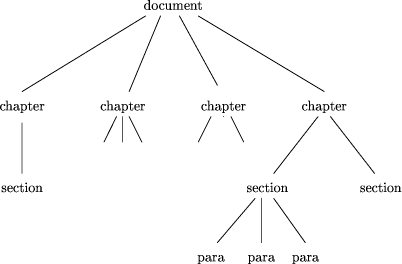
is itself an object built up from smaller objects, say b = c h(b) = h(c) and so h(a Page 43 The structure of the computation follows the structure of the argument. Second, the evaluations of h on the right hand sides are independent and can therefore be evaluated in parallel if the architecture permits it. These simple ideas lead to a rich approach to parallel computation. Homomorphisms include many of the interesting functions on constructed data types. In particular, all injective functions are homomorphisms. Furthermore, all functions can be expressed as almost-homomorphisms [Col93], the composition of a homomorphism with a projection, and this is often of practical importance. Skeletons are an important approach to parallel computing, beginning from the work of Cole [Col89]. Homomorphic skeletons are particularly attractive because they come equipped with a useful transformation system, including a guarantee of expressive completeness [Ski94]. In the next section we review the construction of a type for trees and show how it may be used to represent structured text. We show how the explicit use of data types reduces algorithm design for homomorphisms to the simpler problem of finding component functions, and illustrate a recursive parallel schema for computing homomorphisms on trees. In Section 3, we distinguish four special kinds of homomorphisms that capture common patterns for information flow in tree algorithms, and for which optimized implementations are worth building. These are: tree maps, tree reductions, upwards and downwards accumulations. In the subsequent five sections we illustrate the application of tree homomorphisms of increasing sophistication, beginning with the computation of global document properties, then search problems (that is, query evaluation), and finally problems that involve communicating information throughout documents. We conclude by discussing the practical implementation of these algorithms on today's architectures, and those likely in the future. 2 Parallel Operations on TreesWe build the type of homogeneous binary trees, that is trees in which internal nodes and leaves are all of the same type. Binary trees are too simple to represent the full structure of tagged texts, since any tagged entity may contain many subordinate entities, but it simplifies the exposition without affecting any of the complexity results. In SGML an entity is delimited by start and end tags. The region between the start and end tags is either `raw' text or is itself tagged. The structure is hierarchical, and can be naturally represented by a tree whose internal nodes represent tags, and whose leaves represent `raw' data. All nodes may contain values for attributes. In particular, tags often have associated text - for example, chapter tags contain the text of the chapter heading as an attribute, figure tags contain figure captions, and so on. Thus a typical document can be represented as a tree of the kind shown in Figure 1. In some kinds of documents, such as this paper, most of the text tends to be near the leaves of the tree. In others, such as reference works and linguistic corpora, there is likely to be a much more even distribution of text among the levels of the tree. Document archives can also be modelled by trees, in which nodes near the root represent document classifications, as shown in Figure 2. The advantage of treating an entire archive as a single tree, whose documents are subtrees, is that Page 44
queries over the entire archive can be treated in exactly the same way as queries about a single document. For example, a query asking for the occurrence of some pattern in a class of documents uses the same syntax, and is about the same complexity, as a query asking for a pattern in a single document. Furthermore, there is no a priori commitment to a particular granularity of partitioning for distribution across parallel storage - it might be sensible to do so at the document level, but it might not. We build trees, using the construction of Gibbons [Gib91], over some base type A that can model entities and their attributes. For our purposes this is a tuple consisting of an entity name and a set of attributes. In our particular examples it will suffice to have one attribute, the string of text associated with each node of the document. Trees representing structured text have arbitrary degree. Fortunately there is a natural way to transform a tree of arbitrary degree into a binary one [Knu73] and this transformation can be incorporated into the algorithms described here in a straightforward way [Ski]. Thus we will, for simplicity, describe the algorithms in the rest of the paper using binary trees. Trees have two constructors:
The first constructor, Leaf, takes a value of type A and makes it into a tree consisting of a single leaf. The second constructor, Join, takes two trees and a value of type A and makes them into a new tree by joining the subtrees and putting the value of type A at the internal node generated. Thus a tree is either a single leaf, or a tree obtained by joining two subtrees together with a new Page 45 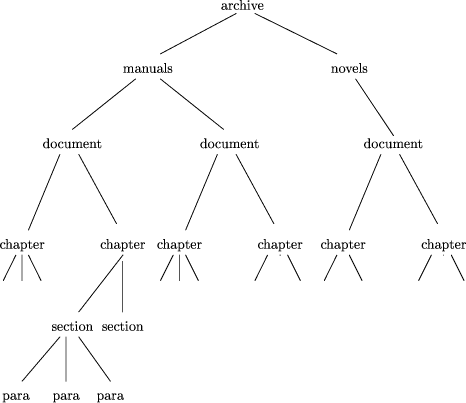
value at the join. A constructor expression describing a tree and the tree itself are shown in Figure 3. Definition 1 [Ski94] A homomorphism, h, on trees is a function that respects tree structure, that is there must exist functions f1 and f2 such that h(Leaf(a)) = Leaf(f1 (a)) and h(Join(t1 , a, t2 )) = f2 (h(t1 ), a, h(t2 )) Call f1 and f2 component functions of the homomorphism h. Furthermore there is a unique correspondence between homomorphisms and their component functions. Here f2 is the glueing function that relates the
effect of h on pieces of the argument to its effect on the whole
argument. Notice that if h has type Page 46
Join(Join(Leaf(d), b, Leaf(e)), a, Leaf(c)) Figure 3: A Constructor Expression and the Tree it Describes finding h means being aware of the structure of Tree(A), which is usually complex, whereas f1 and f2 are operations on (usually) simpler types and are easier to find. This is a considerable practical advantage. The unique correspondence between homomorphisms and their component functions justifies the notation h = Hom(f1 , f2 ) for the (necessarily unique) tree homomorphism from (Tree(A), Leaf, Join) to the algebra (P, f1 , f2 ). We can now make formal the recursive computation of h that we saw earlier. The recursive schema for evaluating all tree homomorphisms is shown in pseudocode in Figure 4. The two recursive calls to eval_tree_homomorphism can be eval_tree_homomorphism( f1, f2, t )
case t of { pattern match on structure of argument }
Leaf(a) :
return f1( a ) ;
Join(Tree(t1), a, Tree(t2)) :
return f2(
eval_tree_homomorphism( f1, f2, t1 ),
a,
eval_tree_homomorphism( f1, f2, t2 ) )
end case
end
Figure 4: Tree Homomorphism Evaluation Schema executed in parallel. Using this simple approach to parallelism, all tree homomorphisms can be evaluated in parallel time proportional to the height of the tree (if f1 and f2 take only constant time). Here are some simple examples of tree homomorphisms: Page 47 Example 1. The tree homomorphism that computes the number of leaves in a tree replaces the value at each leaf by the constant 1, and then sums these values over the tree. It is given by number-of-leaves = Hom(K1 , f2 ) where eval_tree_homomorphism( t )
case t of
Leaf(a) :
return K_1 ( a ) ; { = 1 }
Join(Tree(t1), a, Tree(t2)) :
return
eval_tree_homomorphism( t1 )
+
eval_tree_homomorphism( t2 )
end case
end
Example 2. The tree homomorphism that finds the maximum value in a tree does nothing at the leaves and at internal nodes selects the maximum of the three values from its two subtrees and the node itself. It is treemax = Hom(id, max) where max is ternary maximum. The fact that all tree homomorphisms are the same in some sense is useful in two ways. First, finding tree homomorphisms reduces to finding component functions. Since component functions describe local actions at the nodes of trees, they are usually simpler conceptually than homomorphisms. There is a separation between common global tree structure and detailed node computations. Second, there is a common mechanism for computing any homomorphism, so it makes sense to spend time optimising that, rather than developing a variety of ad hoc techniques. Nevertheless, there are some classes of homomorphisms for which better implementations are possible. These classes have many members that are of practical interest. 3 Four Classes of Tree HomomorphismsThere are four special classes of homomorphisms that are paradigms for common tree computations. They are: tree maps, tree reductions, and two forms of tree accumulations, upwards and downwards. In our discussion of implementations, we will assume either the EREW PRAM or a distributed-memory hypercube architecture as the target computer. The EREW PRAM does not charge for communication, and our implementations can all be arranged on the hypercube so that communication is always Page 48 with nearest neighbours, except for the tree contraction algorithm used in several places. This enables us to include communication costs in our complexity measures. We use a result of Mayr and Werchner [MW93] to justify the complexity of tree contraction on the hypercube. We will also assume that a tree of n nodes is processed by an n-processor system, so that there is a processor per tree node. We return to this very unrealistic assumption later. A tree map is a tree homomorphism that applies a function
to all the nodes of a tree, but leaves its structure unchanged. If f
is some function 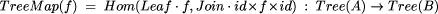
The recursion implicit in evaluating a map as a homomorphism ``unpacks'' the argument tree into a set of leaves and internal nodes. These are then joined back together in exactly the same structure, except that the function f is applied to each value before it is placed back in the tree. The resulting tree has exactly the same shape as the argument tree; only the values (and types) at the leaves and internal nodes have changed. This implementation is therefore unnecessarily cumbersome. A tree map can be computed directly by skipping the disassembly and subsequent reassembly and just applying f to each leaf and internal node, without any communication. Let ti(f) denote the time complexity of f in i processors. The sequential complexity of a tree map is given by t1 (TreeMap(f)) = n x t1 (f) and the parallel complexity by tn (TreeMap(f)) = t1 (f) A tree reduction is a tree homomorphism that replaces structure without explicitly manipulating values. Applied to a tree, a tree reduction most often produces a single value. Formally, a tree reduction is a tree homomorphism
where the type of g is
Figure 5 shows a tree and the result of applying a reduction to it. Knowing the result of the reduction on subtrees, the result of the reduction on the tree formed by joining them requires a further application of g, so that critical path is the application of gs along the longest branch. Thus tree reduction takes parallel time proportional to the height of the tree in the worst case. The sequential complexity of tree reduction is t1 (TreeReduce(g)) = n x t1 (g) and the parallel complexity is tn (TreeReduce(g)) = ht x t1 (g) where ht is the height of the tree. Page 49
Somewhat surprisingly, tree reduction can be computed much faster for many kinds of functions g. For theoretical models such as the EREW PRAM and more practical architectures such as the hypercube, tree reduction can be computed in time logarithmic in the number of nodes of the tree, subject to some mild conditions on the function g [ADKP87, MW93]. This is a big improvement over the method suggested above, since a completely left- or right-branching tree with n nodes requires time proportional to n to reduce directly, whereas the faster algorithm takes time log n. The key to fast tree reduction is making some useful progress towards the eventual result at many nodes of the tree, whether or not the reductions for the subtrees of which they are the root have been completed. Naive reduction applies g only at those nodes both of whose children are leaves. However, for well-behaved reduction operations it is possible to carry out partial reductions for nodes only one of whose descendants is a leaf. We begin by defining a contraction operation that applies to any
node and its two descendants, if at least one descendant is a leaf. Suppose
that each internal node u contains a pointer u.p to its parent,
a boolean flag u.left that is true if it is a left descendant, a
boolean flag u.internal that is true if the node is an internal
node, a variable u.g describing an auxiliary function of type We describe an operation that replaces u, u.l, and u.r, where u.l is a leaf, by a single node u.r as shown in Figure 6. A symmetric operation contracts in the other direction when u.r is a leaf. The operations required are  The first step is the most important one. It `folds' in an application of f2 so Page 50 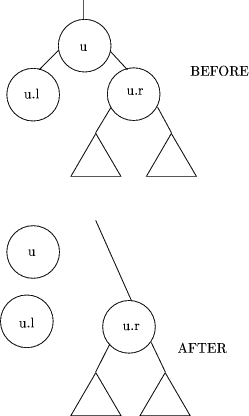 Figure 6: A Single Tree Contraction Step: Nodes u and u.l are deleted from the tree, and u.r is updated that the function computed at node u.r after this contraction operation is the one that would have been computed at u before the operation. The contraction algorithm will only be efficient if this step is done quickly and the resulting expression does not grow long. We will return to this point below. The contraction operations must be applied to about half of the leaves on each step if the entire contraction is to be completed in about a logarithmic number of steps. The algorithm for deciding where to apply the contraction operations is the following:
Page 51 part. Sufficient conditions for preventing the lambda expressions in the u.gs from growing large are the following [ADKP87]
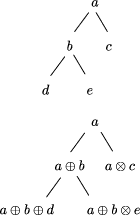
These conditions ensure three properties: that no function built at a node takes more than constant time to derive from the functions of the three nodes it is replacing, that no such function takes more than constant time to evaluate, and that no such function requires more than a constant amount of storage. Together these three properties guarantee that the tree contraction algorithm executes in logarithmic parallel time. Thus we have a parallel time complexity for tree reduction of tn (TreeReduce(g)[tree contraction]) = log n since t1(g) must be O(1). The third useful family of tree homomorphisms are upwards accumulations. Upwards accumulations are operations in which data can be regarded as flowing upwards in the tree, and where the computations that take place at each node depend on the results of computations at lower nodes. These are like tree reductions that leave all their partial results in place. The final result is a tree of the same shape as the argument tree, in which each node holds the result of a tree reduction rooted at that node. They are thus analogous to parallel prefix or scan computations on lists. This is illustrated in Figure 7. Upwards accumulations are characterized as follows. Let subtrees be the function that replaces each node of a tree by the subtree rooted at that node. Hence it takes a tree and produces a tree of trees. Although subtrees is a messy and expensive function, it is still a homomorphism. Upwards accumulations are those functions that can be expressed as the composition of subtrees with a tree homomorphism mapped over the nodes of the intermediate tree.
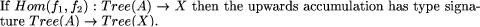 Computing an upwards accumulation in the way implied by this definition is expensive. The point of defining upwards accumulations like this is that the result at any node shares large common expressions with the results at its immediate descendants. Therefore, the number of partial results that must be computed in an upwards accumulation is linear in the number of tree nodes. Thus it is possible that there is a fast parallel algorithm, provided the dependencies introduced by Page 52 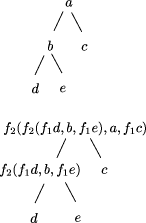 the communication involved are not too constraining; and indeed there is. The algorithm is an extension of tree contraction; when a node u is removed, it is stacked by its remaining child. When this child receives its final value, it unstacks u and computes its final value. Details may be found in [GCS94]. The sequential time complexity of an upwards accumulation is t1 (UpAccum(f1 , f2 )) = n(t1 (f1) + t1 (f2 )) its parallel time complexity is tn (UpAccum(f1 , f2 )) = t1 (f1) + ht x t1 (f2 ) and its parallel time complexity using extended tree contraction is tn (UpAccum(f1 , f2 )[tree contraction]) = log n because f1 and f2 must be O(1). The fourth useful family of tree homomorphisms are the downwards accumulations. Downwards accumulations replace each node of a tree by some function of the nodes on the path between it and the root. This models functions in which the flow of information is broadcast down through the tree. We first define the type of non-empty paths, which are like lists except that they have two concatenation constructors, left turn, L, and right turn, R. This type models the paths that occur between the root of a tree and any other node, where it is important to remember whether the path turns towards a left or right descendant at each step. The two constructors are mutually associative, that is (a?b)??c = a?(b??c) where ? and ?? are either of the constructors. Homomorphisms on paths have component functions
Page 53 where
A downwards accumulation is shown in Figure 8. The value that results at
Figure 8: A Downwards Accumulation each node of the tree depends on the values of the nodes that appear in the path between the node and the root, together with their structural arrangement, that is, the combination of left and right turns that appear along the path. Note that the asymmetric treatment inherited from left and right turns means that downwards accumulations include functions whose value depends not only on the content of nodes but also on their relative positions in the tree. Clearly it is expensive to compute a downwards accumulation by computing all of the paths and then mapping a path reduction over them. However, there are again large common expressions between each node and its parent, so that the total number of expressions to be computed is linear in the size of the tree. As a result, there is an algorithm that runs in parallel time proportional to the logarithm of the number of the nodes in the tree [GCS94]. The sequential time complexity of a downwards accumulation is
its parallel time complexity is
Page 54 and its parallel time complexity using extended tree contraction is
because The parallel complexity results so far have been based on the assumption of one processor per document node. This is clearly unrealistic. However, all of these homomorphisms can be adapted to use fewer processors by allocating a region of each tree to each processor, which then applies a modified homomorphism to that region. The actual partitioning is complex, because a partition of a tree into regions is not normally itself a tree. However, with some care it is possible to get implementations of the fast parallel operations above in time complexity n/p + log p for trees of size n using p processors [Ski]. For small p, this gives almost linear speed-up over sequential implementations, while for large p it gives almost logarithmic execution times. 4 Global Properties of DocumentsWe now have a set of homomorphic tree operations that can be evaluated in parallel effectively. We now begin to show how these operations can be applied to structured text. We begin with operations that are tree maps or tree reductions. A broad class of such operations are those that count the number of occurrences of some text or entity in a document. In such tree homomorphisms, the pair of functions used are of the general form f1 (a) = if (a = entity name) then 1 else 0 f2 (t1 , a, t2 ) = t1 + t2 + (if (a = entity name) then 1 else 0) with types
Some tree operations can be factored into the composition of a tree map and a tree reduction. This is often an easy way to understand and compute the complexity of a homomorphism. Notice that f2 above can be written as
where
The tree map can be computed in a single parallel step, taking time t1 (f1). The tree reduction step can be computed using tree contraction in a logarithmic number of steps, each involving an application of functions related to f2, Page 55 taking time log n. Thus the total parallel time complexity of evaluating this tree homomorphism is tn (total time) = log n + t1 (f1) (1) The following document properties of frequency can be determined in the parallel time given by Equation 1: - number of occurrences of a word (that is, a delimited terminal string),- number of occurrences of a structure or entity (section, subsection, paragraph, figure), - number of reference points (labels). An extension of these counting tree homomorphisms produce simple data types as results. For example, to produce a list of the different entity names used in a document, we use a tree homomorphism with component functions
that produces a set containing the entity names that are present. Each leaf is replaced by the name of the entity it represents. Internal nodes merge the sets of entity names of their descendants with the name of the entity they represent. Using sets means that we record each entity name only once in the final set. To determine the number of different entities present in a document, we need only to compute the size of the set produced by this tree homomorphism. Changing the set used to a list, we define a tree homomorphism to produce a table of contents. It is
where Another useful class of tree homomorphisms computing global properties are those that compute properties of extent. The most obvious example computes the length of a document in characters. It is f1 (a) = length(a.string) f2 (t1 , a , t2 ) = t1 + t2 + length(a.string) Similarly, the tree homomorphism that computes the deepest nesting depth of structures in a document is f1 (a) = 0 f2 (t1 , a, t2 ) = max(t1 , t2 ) + 1 Page 56 Again their parallel time complexity is given by Equation 1. Software is an example of structured text. Some tree homomorphisms that apply to software are: computing the number of statements, and building a simple (that is, unscoped) symbol table. All of these examples are easy, but they do show how apparently-unrelated operations can be seen as instances of a common pattern. This simplifies their use because they can be presented as parameterised occurrences of a single operation, and simplifies their implementation, since many of the necessary decisions need only be made once. 5 Search ProblemsAnother important class of operations on structured text involve searching them for data matching some key. Four levels of search can be distinguished:
Page 57 all occurrences of ``dog'' and all tags associated with the beginning
and ending of sections and chapters, and then processing them to find those
that are correctly contained. Finding an occurrence of ``dog'' within the
seventh section of the third chapter requires looking up a large amount
of information, and complex processing of it. As we will show, this fourth level of search is no more expensive to implement in parallel than the previous three. Thus even if parallelism does not provide absolute performance improvements because of limits on disk speeds, it can provide improvements in functionality. We explore this style of search further in the next two sections. 6 Accumulations and Information TransferAccumulations allow nodes to find out information about all their neighbours in a particular direction. Upwards accumulation allow each node of a tree to accumulate information about the nodes below it. Downwards accumulations allow each node to accumulate information about those nodes that lie between it and the root. Powerful combination operations are formed when an upwards accumulation is followed by a downwards accumulation, because this makes arbitrary information flow between nodes of the tree possible. As we have seen, both kinds of accumulations can be computed fast in parallel if their component functions are well-behaved. Some examples of upwards accumulations are: computing the length in characters of each object in the document; and computing the offset from each segment to the next similar segment (for example the offset from each section heading to the next section heading). Some examples of downwards accumulations are: structured search problems, that is searching for a part of a document based on its content and its structural properties; and finding all references to a single label. Structured search is so important that we investigate its implementation further in the next section. Gibbons gives a number of detailed examples of the usefulness of upwards followed by downwards accumulations in [Gib91]. Some examples that are important for structured text are: evaluating attributes in attribute grammars (which can represent almost any property of a document); generating a symbol table for a program written in a language with scopes; rendering trees, which is important for navigating document archives; determining which page each object would fall on if the document were produced on some device; determining which node the ith word in a document is in, and determining the font of each object (in systems where font is relative not absolute, such as LATEX). Operations such as resolving all cross references and determining all the references to a particular point can also be cast as upwards followed by downwards accumulations, but the volume of data that might be moved on some steps makes this expensive. Page 58 7 Parallel String Search of Flat Text and TreesThere is a well-known parallel algorithm for recognizing whether a given string is a member of a regular language in time logarithmic in the length of the string [Fis75,HS86]. This algorithm is naturally parallel and readily adapted to document search, even on quite modest parallel computers. Although it was described for the Connection Machine [HS86] it seems never to have been used on any real parallel system. It is related to the technique used by Hollaar [Hol85, Hol91], but is more expressive, since the use of special-purpose hardware limits the flexibility of Hollaar's searches. We review the parallel algorithm and show how it allows queries that are regular expressions, and hence can search for patterns involving both content and tags. We then show how to extend it to a parallel search algorithm for trees. Suppose that we want to determine if a given string is a member of a regular language over an alphabet {a, b, c}. The regular language can be defined by a finite state automaton, whose transitions are labelled by elements of the alphabet. This automaton is preprocessed to give a set of tables, each one labelled with a symbol of the alphabet, and consisting of pairs of states such that the labelling symbol labels a transition from the first pair in each state to the second. For example, given the automaton in Figure 9, the tables are:
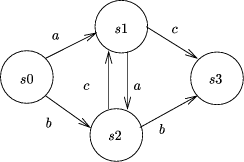
Figure 9: A Simple Finite State Automaton
The homomorphism (on lists) consists of two functions:
Page 59 It will be convenient to write f2 as an infix binary
operation,
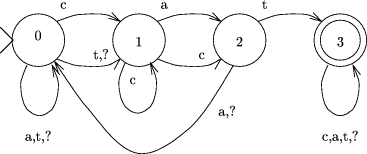
At the end of the reduction, the single resulting table expresses the effect of the entire input string on states. If it contains a pair whose first element is the initial state and whose second element is a final state, the string is in the regular language. All of the tables are of finite size (no larger than the number of transitions in the automaton). Each table composition takes no longer than quadratic in the number of states of the automaton. The reduction itself takes time logarithmic in the size of the string being searched on a variety of parallel architectures [Ski90]. The regular language recognition problem is readily adapted for query processing (although there are some subtleties [CC95]). Suppose we wish to determine if some regular expression, RE, is present in an input string. This regular expression defines a language, L(RE), that is then extended to allow for the existence of other symbols and for the string described by the regular expression to appear in a longer string. Call this extended language L(RE)'. Then the search problem becomes: is the text s in the language L(RE)' ? There is a finite state automaton corresponding to L(RE)' . It is based on the finite state automaton for L(RE) with the addition of extra transitions labelled with symbols from the extended alphabet. It can be as large as exponential in the size of the regular expression, but is independent of the size of the string being searched. An example of the automaton corresponding to the search for the word ``cat'' is shown in Figure 10 and the resulting algorithm on an input string ``bcdabcat'' in Figure 11.
Figure 10: Finite State Automaton for ``cat'' Page 60
Figure 11: Algorithm Progress for the Search Queries that are boolean expressions of simpler regular language queries could be evaluated by evaluating the simple queries independently and then carrying out the required boolean operations on the results. However, the closure of the class of regular languages under union, intersection, complementation, and concatenation means that such complex queries can be evaluated in a single pass through the data by constructing the appropriate deterministic finite state automaton. For example, a query of the form ``are x and y in the text'' amounts to asking if the text is a string of the augmented language of the intersection of the regular languages of the strings x and y. We now show how regular language recognition for strings may be generalized to trees. The first step applies a tree map that replaces each node of the tree by a table, mapping states to states, that is the tree homomorphism:
The second step is a tree reduction, in which the tables of a node and its two subtrees are composed using a ternary generalisation of the composition operator used in the string algorithm above:
where table composition has been generalized to a ternary operation
Notice that the composition of tables composes the table belonging to the internal node first, followed by the tables corresponding to the subtrees in order. Page 61 This represents the case where the text in the internal node represents some kind of heading. The order may or may not be significant in an application, but care needs to be taken to get it right so that strings that cross entity boundaries are properly detected. The extension of the search in a linear string to a tree is shown in Figure 12. This algorithm takes parallel time logarithmic in the number of nodes of the tree, using the tree contraction algorithm discussed in the previous section. The automaton can be extended as before to solve query problems, giving a fast parallel query evaluator for a useful class of queries. Query evaluation problems that are of this kind include: word and phrase search, and boolean expressions involving phrase search. Such queries are of about the complexity of those permitted by the PAT system. Because the tree structure of structured text encodes useful information, we now turn to extending this search algorithm to a new kind of search in which not only the presence of data but also its relationships can be expressed in the query. This increases the power of the query language substantially. It turns out that such structured queries can still be computed in parallel within logarithmic time bounds, making structured queries of practical importance. 8 Parallel Structure Search of TreesQueries on structured text involve finding nodes in the tree based on information about the content of the node (its text and other attributes) and on its context in the tree, particularly its relative context such as ``the third section''. Here are some examples, based on [Mac91]: Example 3. document where (`database' in document) Example 4. document where (`Smith' in Author) Example 5. Section of document where (`database' in document) Example 6. Section of document where (`database' in SectionHeading) All of these queries describe patterns in the tree; patterns may include ``don't care''s in both the nodes and the branch structure. Queries are relative to a Page 62 
Page 63 particular node in the tree (usually the root) and return a bag of nodes corresponding to the roots of trees containing the pattern (bags are sets in which repetitions count; we want to know all the places where a pattern is present, so the result must allow for more than one solution). Allowing queries to take a bag of nodes as their inputs, so that searches begin from all of these nodes, allows queries to be composed. Note that a node is precisely identified by the path between itself and the root, so we might as well think of node identifiers as paths. There are two different kinds of bag operations in the query examples above. The first are filters that take a bag of nodes and return those elements of the bag that satisfy some condition. The second are moves that take a bag of nodes and return a bag in which each node has been replaced either by a node related to it (its ancestor, its descendant, its sibling to the right) or by one of its attributes. A simple query is usually a filter followed by the value of an attribute at all the nodes that have passed the filter. More complex queries such as the last example above require more complex moves. This insight is the critical one in the design of path expressions [Mac93], a general query language for structured text applications. The crucial property of path expressions that we require is that filters can be broken up into searches for patterns that are single paths, and are therefore expressible as regular expressions over paths. Such filters can be computed by replacing each node of the structured text tree by the path from it to the root, and then applying the regular string recognition algorithm, extended to include left and right turns, to each of these paths. Those nodes for which the string recognition algorithm returns True are the nodes selected by the filter. For example, a query about the presence of a chapter whose first section contains the word ``About'' is equivalent to asking if there is a path in the tree that contains the following: 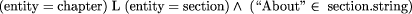
A tree annotated with left and right turns is shown in Figure 13, and the result of applying the paths function to it is shown in Figure 14. The regular language recognition algorithm for strings can be extended
to paths straightforwardly. The query string may contain references to
right and left turns, and so may the extended regular language. Otherwise
the operations of table construction and binary table composition ( Filters can be expressed as 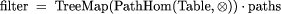 The right hand side replaces the text tree with the tree in which each node contains the path between itself and the root. The TreeMap then maps the regular language recognition algorithm for paths over each of these nodes. Those that find an instance of the string are the roots of subtrees that correspond to the query pattern. But we have already seen that operations that can be expressed as maps over paths are downward accumulations, and hence can be computed efficiently in parallel when the component functions are well-behaved. We have also seen that table composition is a constant-time, associative function and so satisfies Page 64 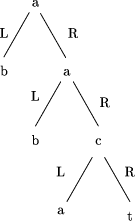 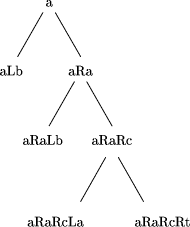 the requirements for tree contraction. Thus there is a logarithmic time parallel algorithm for computing such filters tn (f ilter) = log n Path expression queries may therefore be included in structured text systems without additional cost, dramatically improving the sophistication of the way in which such resources can be queried. The algorithm above may be adapted to run on p (p < n) processors, with parallel time complexity n/p + log p. It can also be extended to multiple trees Page 65 sharing structure, such as those which arise in corpus linguistics and multiple document views [RS]. 9 Implementing Path Expression SearchThe parallel search algorithm described in the previous section is not, at present, competitive with existing index-based search algorithms. There are two reasons. The first is that the current generation of parallel machines does not effectively integrate disk storage with processors, although this is changing. Instead, a set of processors is typically connected to an array of disks via a high-bandwidth switch. Thus there is no locality of reference. The algorithm described here carefully partitions data and computations in a way that is balanced and requires little communication. This care cannot be taken advantage of on today's architectures. However, within a decade parallel architectures can be expected to provide substantial disk storage local to each processor. When that happens, our algorithm will be more useful. The second reason why our algorithm is not competitive is that, in common with most parallel algorithms, it traverses the whole structure being searched. In contrast, algorithms based on inverted indexes, and simple parallel adaptations of them, avoid this, at the expense of creating and storing large indexes. Although almost nothing is know about indexing structures in a way that would improve the performance of parallel algorithms, there is some hope that new techniques [Ski95] will reduce this handicap. Our algorithm may also be useful in situations where the text archive is highly dynamic, making indexing impractical. It is also the case that most document structure resides within single files, perhaps connected in a hierarchical directory structure. Thus the logical structure implied by SGML does not match the physical structure well. This is changing as new file structure mechanisms, such as DFR [ISO87], are developed, in response to the acknowledged weakness of hierarchical file structures. 10 ConclusionsThe SGML approach of structural tagging of entities makes it possible to model structured text as a data type. This in turn makes it possible to use the machinery of categorical data types to describe trees and to express and compute homomorphic skeletons on trees. The underlying regularities that this exposes reveals the similarities between apparently different operations on structured text, shows how their discovery and construction can be simplified to the construction of component functions, and suggests both sequential and parallel implementations for them. In particular we have shown how tree contraction and its extensions can be used to build fast parallel implementations of standard text processing techniques. A major contribution of the paper is the discovery of a fast parallel implementation for searches based on path expressions. These allow much simpler implementations of sophisticated searching than existing query languages and may eventually be able to provide better performance. The algorithm is of theoretical interest as the first novel algorithm to be found using the categorical data type approach. It is unlikely that this algorithm would have been found Page 66 from first principles. This adds support for the idea that homomorphisms on data types are useful tools for finding parallel algorithms. References[ADKP87] K. Abrahamson, N. Dadoun, D.G. Kirkpatrick, and T. Przytycka. A simple parallel tree contraction algorithm. In Proceedings of the Twenty-Fifth Allerton Conference on Communication, Control and Computing, pages 624-633, September 1987. [Bir87] R.S. Bird. An introduction to the theory of lists. In M. Broy, editor, Logic of Programming and Calculi of Discrete Design, pages 3-42. Springer-Verlag, 1987. [CC95] C.L.A. Clarke and G.V. Cormack. On the use of regular expressions for searching text. Technical Report CS-95-07, Department of Computer Science, University of Waterloo, February 1995. [Col89] M. Cole. Algorithmic Skeletons: Structured Management of Parallel Computation. Research Monographs in Parallel and Distributed Computing. Pitman, 1989. [Col93] M. Cole. Parallel programming, list homomorphisms and the maximum segment sum problem. In D. Trystram, editor, Proceedings of Parco 93. Elsevier Series in Advances in Parallel Computing, 1993. [CV89] R. Cole and U. Vishkin. Faster optimal parallel prefix sums and list ranking. Information and Control, 81:334-352, 1989. [FC84] C. Faloutsos and S. Christodoulakis. Signature files: An access method for documents and its analytical performance evaluation. ACM Transactions on Office Information Systems, 2:267-288, April 1984. [Fis75] Charles N. Fischer. On Parsing Context-Free Languages in Parallel Environments. PhD thesis, Cornell University, 1975. [GBYS92] G.H. Gonnet, R.A. Baeza-Yates, and T. Snider. New indices for text: PAT trees and PAT arrays. In W.B. Frakes and R. Baeza-Yates, editors, Information Retrieval: Data Structures and Algorithms, pages 66-82. Prentice-Hall, 1992. [GCS94] J. Gibbons, W. Cai, and D.B. Skillicorn. Efficient parallel algorithms for tree accumulations. Science of Computer Programming, 23, No.1:1-18, 1994. [Gib91] J. Gibbons. Algebras for Tree Algorithms. D.Phil. thesis, Programming Research Group, University of Oxford, 1991. [Hol85] L. Hollaar. The Utah Text Search Engine: Implementation experiences and future plans. In Database Machines: Fourth International Workshop, pages 367-376. Springer-Verlag, 1985. [Hol91] L. Hollaar. Special-purpose hardware for text searching: Past experience, future potential. Information Processing and Management, 27:371-378, 1991. [HS86] W. Daniel Hillis and G.L. Steele. Data parallel algorithms. Communications of the ACM, 29, No.12:1170-1183, December 1986. [Inc86] Fulcrum Technologies Inc. Ful/text reference manual. Fulcrum Technologies, Ottawa, Ontario, Canada, 1986. [ISO86] ISO. Information processing - text and office systems - standard generalized markup language (SGML), 1986. [ISO87] International Organisation for Standardisation. Information Processing Systems - Document Filing and Retrieval, 1987. ISO/TC 97/SC 18/WG 4. [Knu73] D.E. Knuth. The Art of Computer Programming, Volume I: Fundamental Algorithms. Addison-Wesley, 1973. Page 67 [Mac91] I.A. Macleod. A query language for retrieving information from hierarchical text structures. The Computer Journal, 34, No.3:254-264, 1991. [Mac93] I.A. Macleod. Path expressions as selectors for non-linear text. Preprint, 1993. [MW93] E.W. Mayr and R. Werchner. Optimal routing of parentheses on the hypercube. In Proceedings of the Symposium on Parallel Architectures and Algorithms, June 1993. [RS] S. Raju and D.B. Skillicorn. Fast querying of concurrent hierarchies. submitted. [SB88] G. Salton and C. Buckley. Parallel text search methods. Communications of the ACM, 31:203-215, 1988. [SC95] D.B. Skillicorn and W. Cai. A cost calculus for parallel functional programming. Journal of Parallel and Distributed Computing, 28(1):65-83, July 1995. [SK86] C. Stanfill and B. Kahle. Parallel free-text search on the Connection Machine. Communications of the ACM, 29:1229-1239, 1986. [Ski] D.B. Skillicorn. Parallel implementation of tree skeletons. Journal of Parallel and Distributed Computing, to appear. [Ski90] D.B. Skillicorn. Architecture-independent parallel computation. IEEE Computer, 23(12):38-51, December 1990. [Ski94] D.B. Skillicorn. Foundations of Parallel Programming. Cambridge Series in Parallel Computation. Cambridge University Press, 1994. [Ski95] D.B. Skillicorn. A generalisation of indexing for parallel document search. Technical Report 95-383, Queen's University, Department of Computing and Information Science, March 1995. [ST91] C. Stanfill and R. Thau. Information retrieval on the Connection Machine. Information Processing and Management, 27:285-310, 1991. [Sto87] H. Stone. Parallel querying of large databases. IEEE Computer, 20, No.10:11-21, October 1987. Page 68 |
|||||||||||||||||||||||||
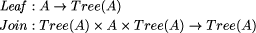
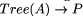 then the types of f1 and f2 are
then the types of f1 and f2 are 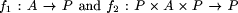 . Thus finding a homomorphism amounts to finding such a pair of functions.
However,
. Thus finding a homomorphism amounts to finding such a pair of functions.
However, 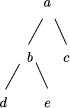
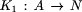 is the constant 1 function
and
is the constant 1 function
and 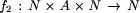 is f2 (t1,
a, t2 ) = t1 + t2 . The recursive
schema specialises to:
is f2 (t1,
a, t2 ) = t1 + t2 . The recursive
schema specialises to: 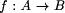 , then TreeMap(f) is the
function
, then TreeMap(f) is the
function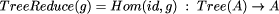
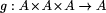
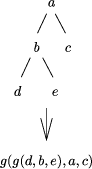
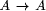 , and, for internal nodes, two pointers, u.l and u.r
pointing to their left and right descendants respectively.
, and, for internal nodes, two pointers, u.l and u.r
pointing to their left and right descendants respectively. 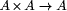 is drawn from an indexed set of functions
F, and the function u.g is drawn from an indexed set of functions
G. Both F and G contain the identity function.
is drawn from an indexed set of functions
F, and the function u.g is drawn from an indexed set of functions
G. Both F and G contain the identity function. 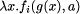 and
and
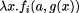 are in G and their indices can
be computed from a and the indices of fi and g
in constant time.
are in G and their indices can
be computed from a and the indices of fi and g
in constant time. 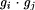 is in G and its indices
can be computed from i and j in constant time.
is in G and its indices
can be computed from i and j in constant time. 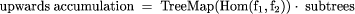
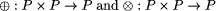
 satisfy the same mutual associativity property.
Define paths to be the function that replaces each node of a tree
by the path between the root and that node. A downwards accumulation is
a tree homomorphism that can be expressed as the composition of paths
with a path homomorphism mapped over the nodes of the intermediate
tree.
satisfy the same mutual associativity property.
Define paths to be the function that replaces each node of a tree
by the path between the root and that node. A downwards accumulation is
a tree homomorphism that can be expressed as the composition of paths
with a path homomorphism mapped over the nodes of the intermediate
tree. 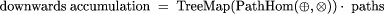
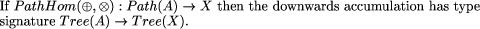
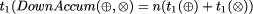
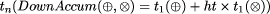
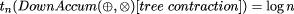
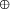 and
and 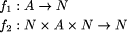
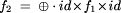
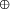 is ternary addition. We can express the `count entities'
homomorphism above as a composition like this:
is ternary addition. We can express the `count entities'
homomorphism above as a composition like this: 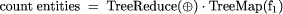
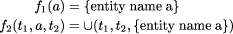
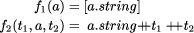
 is list concatenation, and a.string extracts the
string attribute associated with node a. This homomorphisms produces
a list of all of the tag instances in the document in level order. The
parallel time complexity of these tree homomorphisms that produce larger
and larger partial results is not straightforward to compute for two reasons:
the operations of concatenation and set union are not necessarily constant
time, so the computation of f2 will not be; and the size of
lists grows with the distance from the leaves, creating a communication
cost that must be accounted for on real computers
is list concatenation, and a.string extracts the
string attribute associated with node a. This homomorphisms produces
a list of all of the tag instances in the document in level order. The
parallel time complexity of these tree homomorphisms that produce larger
and larger partial results is not straightforward to compute for two reasons:
the operations of concatenation and set union are not necessarily constant
time, so the computation of f2 will not be; and the size of
lists grows with the distance from the leaves, creating a communication
cost that must be accounted for on real computers