Monitoring Temporal Logic Specifications Combined with Time Series Constraints

Abstract: Run-time monitoring of temporal properties and assertions is used for testing and as a component of execution-based model checking techniques. Traditional run-time monitoring however, is limited to observing sequences of pure Boolean propositions. This paper describes tools for observing temporal properties over time series; namely, sequences of propositions with constraints on data value changes over time. Using such Temporal Logic with time Series (TLS), it is possible to monitor important properties such as stability, monotonicity, temporal average and sum values, and temporal min/max values. The specification and monitoring of linear time temporal logic with real-time and time series constraints are supported by the Temporal Rover and the DBRover, which are in-process and remote run-time monitoring tools. The novel TLS extension described in this paper is based on practical experience and feedback provided by NASA engineers after using the DBRover to verify flight code. The paper also presents a novel hybrid approach to verify timing properties in rapid system prototyping that combines the traditional schedulability analysis of the design and the monitoring of timing constraint satisfaction during prototype execution based on a time-series temporal logic. The effectiveness of the approach is demonstrated with a prototype of the fish farm control system software.

Keywords: Temporal Logic, Run-time Execution Monitoring, Rapid Prototyping, Execution-based Model Checking, Real-time Systems

Categories: D.2.1, D.2.4, D.2.5, D.2.6, D.3.1, F.3.1

1 Introduction

Temporal Logic is a special branch of modal logic that investigates the notion of time and order. In [Pnueli 77], Pnueli suggested using Linear-Time Propositional Temporal Logic (LTL) for reasoning about concurrent programs. Since then, several researchers have used LTL to state and prove correctness of concurrent programs, protocols, and hardware (e.g., [Hailpern and Owicki 83], [Manna and Pnueli 81]).

Linear-Time Temporal Logic (LTL) is an extension of propositional logic where, in addition to the propositional logic operators, there are four future-time operators and four dual past time operators: always in the future (always in the past), eventually, or sometime in the future (sometime in the past), until (since), and next cycle (previous cycle).

Metric Temporal Logic (MTL) was suggested by Chang, Pnueli, and Manna as a vehicle for the verification of real time systems [Chang et al. 94]. MTL extends LTL by supporting the specification of relative time and real time constraints. All four LTL future time operators (Always, Eventually, Until, Next) can be constrained by relative time and real time constraints specifying the duration of the temporal operator. For example, {x>0} Until <5 {y>0} means x>0 must be true until a future time, at most 5 real-time units in the future, where y>0 must hold. This paper describes additional extension to LTL and MTL suitable for the specification of time-series constraints.

Run time Execution Monitoring (REM) is a class of methods of tracking temporal requirements for an underlying application. First applications of REM were verification oriented where REM methods were used to track whether an executing system conforms to formal specification requirements. REM is also useful as a component of execution-based model checkers such as the Java Path Finder [Havelund and Pressburger 00]. Recent adaptations of REM methods enable run time monitoring for non-verification purposes such as temporal business rule checking and temporal security rule checking [Drusinsky and Fobes 03]. Unlike previously published methods [Sistla and Wolfson 95], the newer methods are on-line; namely, temporal rules are evaluated without storing an ever growing and potentially unbounded history trace. The Temporal Rover and DBRover tools described in the next section perform on-line REM using executable alternating finite automata. The technique enables on-line monitoring complex Kansas State Specification Pattern assertions at a rate of 6000 to 60,000 cycles per second on a 1GHz CPU [Drusinsky 03], and is capable of monitoring past-time and future-time temporal logic augmented with real-time constraints, time-series constraints, and special counting operators described in [Drusinsky 00]. High-speed on-line REM enables demanding applications such as formal specification based exception handling [Drusinsky 01].

REM is particularly useful in assisting real-time system engineers to evaluate the feasibility of temporal requirements with time-series constraints that must be satisfied over a period of time. When working in tandem with rapid prototyping, REM can be used to debug the requirements and identify errors early in the design process. The hybrid approach described in Section 4 is supported by an environment made up of the Software Engineering Automation Tools (SEATools) [Luqi et al. 01] and the DBRover System. The effectiveness of the approach is demonstrated with a prototype of the fish farm control system software.

2 Run Time Monitoring Tools: The Temporal Rover and DBRover

The Temporal Rover [Drusinsky 00] is a code generator whose input is a Java, C, C++, or HDL source code program, where LTL/MTL assertions are embedded as source code comments. The Temporal Rover parser converts this program file into a new file, which is identical to the original file except for the assertions that are now implemented in source code. The following example contains an embedded MTL assertion for a Traffic Light Controller (TLC) written using the Temporal Rover syntax asserting that for 10 seconds, whenever light is red, camera should be on:

void tlc(int Color_Main, boolean CameraOn) { 
  ... /* Traffic Light Controller functionality */ 
  /* TRBegin 
   TRClock{C1=getTimeInMillis()} // get time from OS 
   TRAssert{ Always({Color_Main == RED} Implies 
               Eventually_C1<10000_{CameraOn == 1}) 
           } => 
      // Customizable user actions 
      {printf("SUCCESS");printf("FAIL");printf("DONE!");}
  TREnd */ 
} /* end of tlc */ 

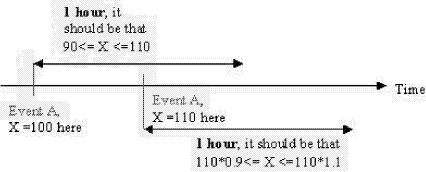
The Temporal Rover generates code that replaces the embedded LTL/MTL assertion with real C, C++, Java, or HDL code, which executes in-process, i.e., as part of the underlying application. The DBRover is a software environment for specifying temporal constraints and remotely monitoring the temporal behavior of the target application. The DBRover consists of a GUI for editing temporal assertions, an MTL simulator, and an MTL execution engine. The DBRover builds and executes temporal rules for a target program or application. In run-time, the DBRover listens for messages from the target application, which are transmitted via HTTP, sockets, or serial communication, and evaluates corresponding temporal assertions. Hence, in the traffic light controller example above, the DBRover will listen for messages pertaining to the run-time values of the CameraOn Boolean propositions, as well as the run-time value of the Color_Main variable. The DBRover then evaluates the corresponding MTL assertion for that cycle. Monitoring is performed on-line, namely, the DBRover operates in tandem with the target program, and re-evaluates assertions every cycle. The DBRover uses an underlying algorithm that does not store a history trace of the data it receives; it can therefore monitor very long and potentially never ending executions of target applications.

The DBRover was used successfully to verify flight code for NASA's Deep Impact project [Drusinsky and Watney 02]. Nevertheless, feedback provided by NASA engineers showed that certain requirements require the ability to specify time-series constraints. The next section describes an extension to LTL and MTL designed for this purpose. The Temporal Rover and DBRover were extended to support this new capability.

3 Improving LTL and MTL: adding Time Series Constraints (TLS)

While LTL and MTL assert about sequences of pure Boolean propositions, it is often required to assert about sequences of propositions over time series, i.e., series of data values with constraints on the change of those values over time. For example, consider a requirement R, stating that for one hour as of eventA, the value of variable x should be 10% stable. Such a requirement combines MTL with propositions based on temporal instances of a variable x. The need for such time series assertions typically involves the validation of statistical and algebraic artifacts such as stability, monotonicity, averaging and expectancy, sum and product values, and min/max values.

Like LTL, TLS assertions are non-deterministic and might have multiple overlapping instances active simultaneously. For example, in requirement R above, the values of a same variable named x are referred to and compared with one another in multiple points in time, for a plurality of eventA's, i.e., for a plurality of initial x values. One of many possible scenarios is where eventA occurs first when x =100, and then occurs again 30 minutes later when x =110; hence, in the overlapping 30 minutes time-segment, x values must range between 99 and 110 (Figure 1). Clearly, the number and timing of eventA occurrences is unknown in advance, and the simple 1-hour end condition is, in general, non-deterministic, rendering the task of monitoring all possible scenarios non-trivial.

TLS enables the specification of requirements in which propositions include temporal instances of variables. Consider the following automotive cruise control code with an embedded stability assertion requiring speed to be 5% stable while cruise is set and not changed (uses the Temporal Rover's source code comments-based syntax):

void cruise(boolean cruiseSet, boolean cruiseChange,
       boolean cruiseOff, boolean cruiseIncr, int speed){
  ... /* Cruise Controller functionality */
  /* TRBegin
      TRAssert{Always ({cruiseSet}Implies 
                {speed*0.95<speed' && speed'<speed*1.05} 
                Until $speed$ {cruiseChange || cruiseOff}
               ) }=> {...} // user actions
  TREnd */
} /* end of tlc */

In this example speed is a temporal data variable, which is associated with the Until temporal operator. This association implies that every time the Until operator begins its evaluation, possibly in multiple instances (due to non-determinism), the speed value is sampled and preserved in the speed variable of this instance of the Until operator; this value is referred to as the pivot value for this Until operator instance.

Future speed values used by this particular evaluation of the Until statement are referred to using the prime notation, i.e., as speed', and are called primed values. Hence, if speed is 100Kmh when cruiseSet is true, then the pivot value for speed is 100, while every subsequent speed value is referred to as speed' and must be within 5% of the (pivot) speed.

Note how speed is declared using the $speed$ notation to be a temporal data variable associated with the Until operator. This declaration indicates to the Temporal Rover that it should be sampling a pivot value from the environment in the first cycle of the Until operators lifecycle, and to refer to all subsequent samples of speed as speed'.

Similarly, the following example consists of a monotonicity requirement for the cruise control system, where speed is monotonically increasing while Cruise Increase (cruiseIncr) command is active:

      TRAssert {Always({cruiseIncr}Implies 
                  {(speed<=speed') && (speed=speed')>=0} 
                  Until $speed$ {!cruiseIncr}
                )}=>  {...} // user actions

In this example the temporal data variable speed is sampled upon the cruiseIncr event, and is compared to the current value (speed') every cycle. The latest speed value is then saved as the pivot for next cycle's comparison.

The following example consists of a temporal averaging and min/max requirement for the cruise control system, requiring that while cruise is set and unchanged, the difference between average speed and minimum speed is always less than 1% of speed.

      TRAssert {Always ({cruiseSet}Implies 
                  {(n++ >=0)&& ((sum+=speed') >= 0) &&
                   ((average=sum/n) >=0) &&
                   ((min=(speed'<min?speed':min) >=0) &&
                   (average-min < speed'/100)
                  } 
                  Until 
                     $speed,min=1000,n=0,average=0,sum=0$
                  {cruiseChange || cruiseOff}
                )}=> {...} // user actions

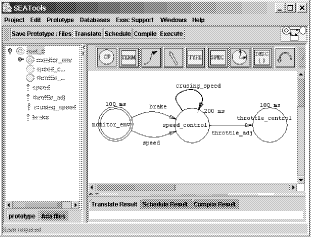
In this example the only data value that is sampled from the environment (the cruise method/function) is speed. All other pivots (i.e., for min, n, average, and sum) are initialized upon the construction of the Until object. Likewise, the only prime value that is sampled from the environment is speed', whereas all other primed variables are assigned as specified in the assignment statements (e.g. as average'=sum'/n'). The Temporal Rover makes this distinction when is recognizes an assignment in the declaration statement, such as sum=0 above.

4 Verifying Timing Properties in Rapid System Prototyping

Real-time systems are those whose correct behavior depends not only on the logical result of the computation but also on the time at which the result is produced. Traditionally, these temporal requirements are expressed as hard and soft timing constraints. It is imperative for real-time systems to meet all deadlines in hard timing constraints but acceptable to miss the deadlines of the soft timing constraints occasionally [Liu 00]. There are currently two complementary approaches to evaluating the correctness of real-time systems: static analysis of its behavior according to a set of metrics (e.g. schedulability analysis to establish the feasibility of the timing constraints) and run-time monitoring of real-time systems to study its behavior according to a set of metrics (e.g. release jitter, frequency and degree of tardiness, etc.). While the static analytic approach plays a very important role in helping system designers set time budgets and allocate resources in their designs, they are only effective if correct timing constraints can be determined during the requirements analysis phase. Feasible requirements for large dynamic systems are difficult to formulate, understand, and meet without extensive prototyping. Moreover, traditional analytical techniques are not effective in evaluating time-series temporal behaviors. These requirements are best evaluated through a hybrid approach that combines the static schedulability analysis of the design and the run-time monitoring of the prototype execution based on TLS. The approach is supported by an environment made up of the Software Engineering Automation Tools (SEATools) and the DBRover.

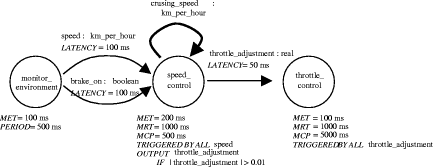
SEATools is based on the Prototyping System Description Language (PSDL) [Luqi et al. 88] [Luqi 93], which is a high-level language designed specifically to support the conceptual modeling of real-time embedded systems. Real-time requirements in the system development are modeled as PSDL specifications, which are dataflow graphs augmented with non-procedural timing and control constraints (Figure 3). PSDL allows the specification of both input and output guards to provide conditional execution of an operator and conditional output of data.

Guards can include conditions on timers that measure duration of system states, and can allow operators to execute only when fresh data has been written to an input stream. Each time critical operator has a maximum execution time (MET) constraint, representing the maximum time the operator may need to complete execution after it is fired, given access to all required resources. In addition, each periodic operator has a period and a deadline (FW). The period is the interval between triggering times for the operator and the deadline is the maximum duration from the triggering of the operator to the completion of its operation. Each sporadic operator has a maximum response time (MRT) and a minimum calling period (MCP). The minimum calling period is the smallest interval allowed between two successive triggering of a sporadic operator. The maximum response time is the maximum duration allowed from the triggering of the sporadic operator to the completion of its operation. An operator can be implemented in either a target programming language or PSDL. An operator with an implementation in the target programming language is called an atomic operator. An operator that is decomposed into a PSDL implementation is called a composite operator. For example, the monitor_environment operator in Figure 3 may be modeled as the graph shown in Figure 4.

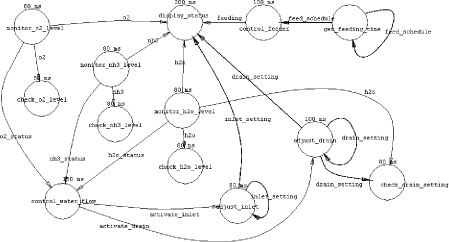
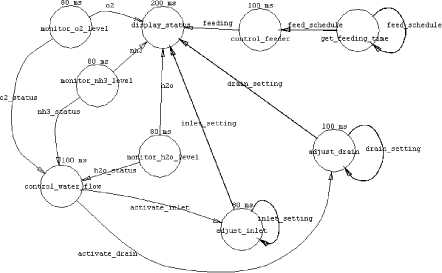
PSDL's declarative timing and control constraints help de-couple the behavioral aspects of a system from its timing properties to allow independent analysis of these two aspects, and organize timing constraints in a hierarchical fashion, to allow independent consideration of smaller subsets of timing constraints.

5 The Fish Farm Control System (FFCS)

In this section, we shall illustrate the hybrid approach with a fish farm control system prototype. The FFCS will control the fish food dispenser and water quality in a fish tank. The tank has a mechanical feeder that drops pellets of fish food from a feeder tube suspended above the tank. The feeder can be turned on and off by the computer. The tank also has a water inlet pipe and a drain pipe with valves controlled by the computer, and sensors that measure the water level (millimeters above the bottom), the oxygen level in the water (parts per million), and the ammonia level in the water (parts per million). The FFCS must deliver fish food at scheduled feeding times, repeated every day. The times when each feeding starts and stops are displayed on the console of the FFCS and can be adjusted from the keyboard. The FFCS must keep the oxygen level at least 8 parts-per-million (ppm), and the ammonia level at most 9 ppm. Fish will die if left in an environment with low oxygen or high ammonia for 1 minute or more. The fish tank is 1 meter wide, 2 meters long, and 1 meter deep (1mm level = 2 liters volume). The FFCS must keep the water level between 60 and 90 cm at all time. The fill/drain valves allow a maximum flow of 0.5 liters per second when valve is fully open. The fresh water coming in the inlet valve contains 30 ppm of oxygen and contains no ammonia. The fish in the tank consumes oxygen at a rate of 0.1 ml/sec and generates ammonia at a rate of 0.0015 ml/sec while resting and at a rate of 0.003 ml/sec while they are eating. The FFCS should minimize water flow subject to the above constraints. In addition, we add another requirement that "when water level is below 88 cm for at least three minutes, the drain valve settings should be limited to be at most 10% of the maximum setting" to illustration the expressive power of the temporal logic.

Figure 5 shows the PSDL model for the FFCS. In the interest of brevity, we shall only discuss the water quality control portion of the prototype in this paper, which is made up of six atomic operators: monitor_h2o, monitor_o2, monitor_nh3, control_water_flow, adjust_inlet and adjust_drain, with the associated control and timing constraints shown in Table 1.

Central to the design is the control_water_flow operator, which controls the inlet and drain water flow based on the following decision table.

Water Level	< 65 cm	65 cm, 85 cm		> 85 cm
Oxygen (O2) & Ammonia (NH3) Level	-	O2 < 8 ppm or NH3 > 9 ppm	O2 8 ppm and NH3 9 ppm	O2 < 8 ppm or NH3 > 9 ppm	O2 8 ppm or NH3 9 ppm
Inlet Valve Setting	open	open	close	open	close
Drain Valve Setting	close	close	close	open	open

To find out if the prototype meets all the requirements using the DBRover System, we formally specify the following temporal rules using TLS:

Rule 1: The water level must be between 60 and 90 cm at all time, formally written as:
              Always {h2o >= 60 && h2o <=90}.

Rule 2: The oxygen level cannot be less than 8 ppm for more than 60 seconds, formally written as:
formally written as:
              Always {o2<8} Implies Eventually <=60 {o2>=8}.

Rule 3: The ammonia level cannot be more than 9 ppm for more than 60 seconds, formally written as:
formally written as:
              Always {nh3>9} Implies Eventually <=60 {nh3<=9}.

Rule 4: If water level has been below 88 cm for 180 seconds, then the change of the drain valve setting must be less than or equal to 10% of the maximum setting (100) per second, formally written as:

      Always( Always >=180 {h2o<=88} Implies 
        Eventually $dv, ffcs_timer$
        { ffcs_timer'==ffcs_timer ||
          abs(dv' - dv)/(ffcs_timer'-ffcs_timer) <= 10}.

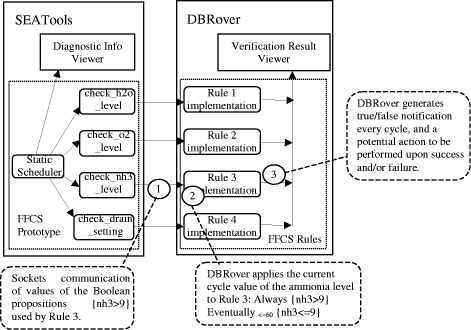
We also add four operators (check_h2o_level, check_o2_level, check_nh3_level, check_drain_setting) to the PDSL model (Figure 6). These operators, when triggered respectively by new data values in the h20, o2, nh3 and drain_setting streams, will send the updated values to the DBRover for temporal property verification during prototype execution (Figure 7). The control and timing constraints of these operators are shown in Table 3.

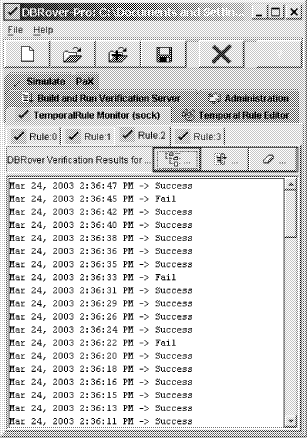
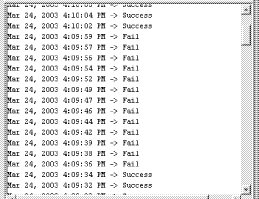
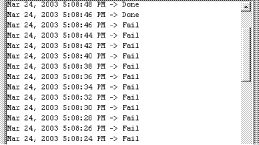
Figure 7: Architecture of the integrated SEATools / DBRover Runtime Monitor System

Figure 8 shows a snapshot of the Temporal Rule Monitor panel of the DBRover system, showing the status of Rule 2 during prototype execution. Each line in the panel represents a new evaluation of the rule, where the top most line represents the latest evaluation. The output from the Temporal Rule Monitor indicated that Rule 2 was invoked by the check_o2_level operator of the FFCS prototype once every 2 seconds (as expected). The timing and logic of the control_water_flow operator (Tables 1 and 2) has caused the oxygen level in the fishpond to fall below 8 ppm roughly once every 10 seconds, but only for a brief duration of at most 2 seconds each time. Output for the other 3 rules (not shown) indicated that the water level, ammonia level and drain valve setting always stayed within the desired limits.

Although the current design satisfied Rule 2, it caused the inlet valve to be turned on (for a duration of 2 seconds) once every 10 seconds, which is bad for the long-term health of the mechanical valve. One way to avoid frequent switching of the valve is by setting the frequency of the control_water_flow operator to longer periods. Through the use of SEATools, we were able to go through the cycle of changing the timing constraints of the operators, translating the PSDL specification into Ada code, compiling the Ada code and executing the prototype in less than 5 minutes. Figure 9 shows a snapshot of the status of Rule 2 when the period of the control_water_flow operator was set to 30 seconds. The new period has caused the oxygen level in the fishpond to fall below 8 ppm roughly once every 2.5 minutes, and for a duration that varied from 3 seconds to 37 seconds. This caused the inlet valve to be turned on (for a duration of 30 seconds) roughly once every 2.5 minutes.

To illustrate the ability for the DBRover Monitor to catch permanent rule violations, we regenerated the executable prototype with the period of the control_water_flow operator set to 60 seconds. Figure 10 showed a snap shot of the status of Rule 2 after executing the prototype for 14 minutes and 17 seconds. The Temporal Rule Monitor detected that the oxygen level fell below 8ppm for more than 1 minute (from 5:07:43 through 5:08:46) and declared a permanent violation (the Done message) of Rule 2 at 5:08:46.

6 Conclusion

While temporal logic specifications and monitoring have been successfully used for the verification of complex reactive systems such as NASA's Deep Impact flight code [Drusinsky and Watney 02], it was found that requirements with time-series constraints such as stability constraints, monotonicity constraints, average-value and expected-value constraints, and sum and product constraints, are all difficult to express in LTL. We have shown an extension of LTL and MTL, named TLS, capable of capturing such requirements. TLS specifications are supported by the Temporal Rover V8.0 and by its remote monitoring counterpart, the DBRover V2.0. The DBRover also includes a graphical simulator for TLS enabling the simulation and debugging of temporal requirements before deploying them on the monitor.

We also show that run-time monitoring, in tandem with rapid prototyping, can be used in verifying temporal properties in the very early stage of the design process. This approach helps identify errors earlier in the design process and also helps debug the requirements themselves. Code generation support by SEATools and Temporal Rover is vital for such approach to be practical. The executable prototype consists 3968 lines of source code, 2048 of which are Ada and C codes generated by the SEATools and the DBRover. The use of socket communication provides a very simple interface between the SEATools runtime environment and the DBRover System. We only need to create one atomic operator in the PSDL model for each temporal rule. The Ada implementation of each of these atomic operators consists of a one-line procedure call to invoke the corresponding C routine implementing the temporal rule. The mapping between the Ada and C code is very straightforward and can be automatically generated easily.

Although the use of socket communication introduces additional time delay between the detection of events during the prototype execution and the checking of the affected temporal properties by the DBRover, it has negligible effect on the accuracy of the verification result because DBRover allows user to specify time based on the client's clock. All events detected during prototype execution are stamped with the local clock before sending to the DBRover for verification.

Acknowledgements

Work done by the first author was supported in part by Naval Postgraduate School Research Initiation Program. Work done by the second author was supported in part by the U.S. Army Research Office under grant number 40473-MA-SP and the U.S. Navy SPAWAR Command under grant number N0003903WRHF02D.

References

[Chang et al. 94] Chang, E., Pnueli, A., Manna, Z.: "Compositional Verification of Real-Time Systems"; Proc. 9th IEEE Symp. on Logic in Computer Science (1994), 458-465.

[Drusinsky 00] Drusinsky, D.: "The Temporal Rover and ATG Rover"; Proc. Spin2000 Workshop, Springer LNCS, 1885 (2000), 323-329.

[Drusinsky 01] Drusinsky, D.: "Formal Specs Can Handle Exceptions"; CMP Embedded Developers Journal (Nov. 2001), 10-14.

[Drusinsky 03] Drusinsky, D.: "On-line Efficient Monitoring of Metric Temporal Logic Specifications using Alternating Automata"; manuscript (2003), submitted for publication.

[Drusinsky and Fobes 03] Drusinsky, D., Fobes, J.: "Real-time, On-line, Low Impact, Temporal Pattern Matching"; Proc. 7th World Multiconference on Systemics, Cybernetics and Informatics, Orlando FL (2003), accepted for publication.

[Drusinsky and Watney 02] Drusinsky, D., Watney, G.: "Applying Run-Time Monitoring to the Deep-Impact Fault Protection Engine"; Proc. 27th IEEE/NASA ICECCS workshop (2002).

[Hailpern and Owicki 83] Hailpern, B., Owicki, S.: "Modular Verification of Communication Protocols"; IEEE Trans of comm., 31, 1 (1983). 56-68.

[Havelund and Pressburger 00] Havelund, K., Pressburger, T.: "Model Checking Java Programs Using Java PathFinder"; International Journal on Software Tools for Technology Transfer (STTT), 2, 4 (2000), 366-381.

[Liu 00] Liu, J.: "Real-Time Systems"; Prentice Hall, 2000.

[Luqi 93] Luqi: "Real-Time Constraints in a Rapid Prototyping Language"; Journal of Computer Languages, 18 (1993), 77-103.

[Luqi et al. 88] Luqi, Berzins, V., Yeh, R.: "A Prototyping Language for Real-Time Software"; IEEE Trans. on Software Eng., 14, 10 (1988), 1409-1423.

[Luqi et al. 01] Luqi, Berzins, V., Ge, J., Shing, M., Auguston, M., Bryant, B., Kin, B.: "DCAPS-architecture for distributed computer aided prototyping system"; Proc. 12th International Workshop on Rapid System Prototyping (2001), 103-108.

[Manna and Pnueli 81] Manna, Z., Pnueli, A.: "Verification of Concurrent Programs: Temporal Proof Principles"; Proc. Workshop on Logics of Programs, Springer LNCS, 131 (1981), 200-252.

[Pnueli 77] Pnueli, A.: "The Temporal Logic of Programs"; Proc.18^th IEEE Symp. on Foundations of Computer Science (1977), 46-57.

[Sistla and Wolfson 95] Sistla, A., Wolfson, O.: "Temporal Conditions and Integrity Constraints in Active Database Systems"; Proc. ACM-SIGMOD 1995 International Conference on Management of Data, San Jose, CA (May 1995).