|
Relativizing Function Classes
Christian Glaßer (Institut für Informatik, Julius-Maximilians-University Würzburg, Germany)
Gerd Wechsung (Institut für Informatik, Friedrich-Schiller-University Jena, Germany)
Abstract: The operators min?, max?, and #? translate classes of the polynomial-time hierarchy to function classes. Although the inclusion relationships between these function classes have been studied in depth, some questions concerning separations remained open.
We provide oracle constructions that answer most of these open questions in the relativized case. As a typical instance for the type of results of this paper, we construct a relativized world where min_P 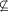 #?NP, thus giving evidence for the hardness of proving min?P #?NP, thus giving evidence for the hardness of proving min?P 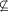 #?NP in the unrelativized case. #?NP in the unrelativized case.
The strongest results, proved in the paper, are the constructions of oracles D and E, such that min_coNPD 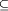 #?PD #?PD  NPD NPD 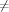 coNPD and UPE = NPE coNPD and UPE = NPE  min?PE min?PE  #?PE. #?PE.
Keywords: function classes, oracle separations, polynomial-time hierarchy
Categories: F.1.3
|