| Submission Procedure |
Formal Specification from an Observation-oriented PerspectiveMeurig Beynon Jaratsri Rungrattanaubol Jane Sinclair Abstract: A formal specification of an algorithm is a very rich mathematical abstraction. In general, it not only specifies an inputoutput relation, but also at some level of abstraction constrains the states and transitions associated with computing this relation. This paper explores the relationship between a formal specification of an algorithm and the many different ways in which the associated states and transitions can be embodied in physical objects and agency. It illustrates the application of principles, tools and techniques that have been developed in the Empirical Modelling Project at Warwick and considers how such an approach can be used in conjunction with a formal specification for exploration and interpretation of a subject area. As a specific example, we consider how Empirical Modelling can be helpful in gaining an understanding of a formal development of a heapsort algorithm. Key Words: Formal specification, invariants, pre and postconditions, agentoriented modelling, dependency, heapsort. Category: F.3.1 1 IntroductionOne current theme of research in theoretical computer science is the way in which different formal (and semiformal) approaches to system development may be combined to provide a more coherent and complete picture of the system under consideration (see, for example, [Hoare and He 1998, Araki et al 1999]). The work of this paper is related to this theme, but broadens the scope by questioning how two very different modelling paradigms may be viewed in relation to each other, and how they can complement each other when used together. The first approach considered is that of formal development. Formal techniques for the development of both software and hardware have evolved over the past 25 years, giving rise to a wealth of different notations and approaches. Such techniques have been used in many areas of industry and, although research Page 407 continues with particular emphasis on usability and scalability, the principles behind them are well understood. Formal approaches have in common a precise, unambiguous syntax with a clearlydefined semantics enabling verification of key properties and of refinement. As an example, we consider a heapsort algorithm derived from a pre/postcondition specification using weakest precondition techniques [Dijkstra 1976]. It is the formal aspect of the approach which is of importance here rather than the specific notation. The second approach we consider is that of Empirical Modelling [EM web] developed over the past 10 years by the Empirical Modelling Research Group in the Computer Science department at the University of Warwick. Whereas a formal specification fixes the important features of the system under development, an Empirical Modelling (EM) approach allows exploration of the state and the effects of dependencies between observables. In this sense it is closer to the requirementsgathering end of the development lifecycle. However, it incorporates tools to enable this exploration which perform a visualisation rôle and may be seen as closer to an environment for rapid prototyping or programming. EM is based on a rather different conceptual framework from formal approaches. It is this important underlying difference which is introduced and explored in this paper. The aim of our work is to examine, with reference to a particular case study, the fundamental differences between the two approaches and the ways in which they may be used together to provide observational motivation for the formal descriptions we develop. This investigation will be carried out from a pedagogical perspective; that is, we concentrate on how the approach can help a student explore and gain an understanding of the basic components and relationships which interact to achieve a required goal. The subject in this case is taken to be a heapsort algorithm, where understanding of such concepts as "is a heap" is needed to master the overall approach. We were able to use existing EM tools with the addition of predicates from the formal development to facilitate this exploration. The two approaches differ fundamentally in their methodology. We use the example to emphasise this and to illustrate the EM philosophy. In the following section the more widely known formal approach is used to introduce the case study. We consider what constitutes a heapsort and how we can recognise and characterise a heapsort activity. Questions also arise concerning how a given specification is interpreted. This leads to a description of the EM approach and the features of using it to explore the heapsort activity. Next, we describe how this model can be extended to incorporate the formal properties, and consider the benefits of exposing students to both mathematical description and interactive exploration. Finally, we discuss what has been achieved by this work and consider some directions for future research. 2 A formal approach to heapsortWhat is heapsort? If we are thinking of a formal description and development of the algorithm we might well start by describing the specification the procedure is required to meet and the data structures it uses. So, if a(1 ... N) is an array of length N with an ordering relation on its elements, we can give a specification of a sorting process in terms of pre and postconditions as follows:
Page 408 That is, our formal description views a heapsort as a process which establishes a "sorted" predicate, with the predicate perm defined to ensure that the final content of the array is a permutation of the original. If it is heapsort in particular that we are interested in, then we also need to introduce the concept of a heap:
The algorithm we have in mind should maintain a heap structure of the elements to be sorted and proceed towards its goal by increasing the number of elements in the sorted segment of the array. When we develop such an algorithm we draw on both our knowledge of the strategy we intend to pursue (e.g. "lengthen the sorted segment of array whilst maintaining heap in unsorted portion") and also on the conditions for correctness in the formal system (e.g. "the invariant of the loop together with the negation of the guard must imply the postcondition"). It is natural to introduce pictures of examples of heaps to explain what is intended. This is also true for describing the workings of the algorithm itself.
A decision on the representation has been made at this stage, the plan being to store the sorted portion in the the higher indexed part of the array. Thus, right from the start, we are rejecting some possible implementations of heapsort and homing in on a particular approach. The unsorted portion will start as the whole of the array and decrease from the upper indices. A variable, n, is introduced to indicate the highest unsorted position so far (N initially). Using a weakest precondition development, the task can be broken down, introducing intermediate goals which fit the algorithm we intend to develop. For example, the plan could be represented as follows.
We could say that an acceptable heapsort program is any one which satisfies
this specification. However, because of the concrete decisions already
made, this excludes many possibilities which would in fact be perfectly
valid heapsort programs. Also, we may feel that the way in which the heap
is reestablished is relevant, since heapsort is generally associated
with a particular compareandswap process. The full development
is not presented here. The remaining tasks from the plan would be developed,
with pre and postconditions calculated to guide each step. The
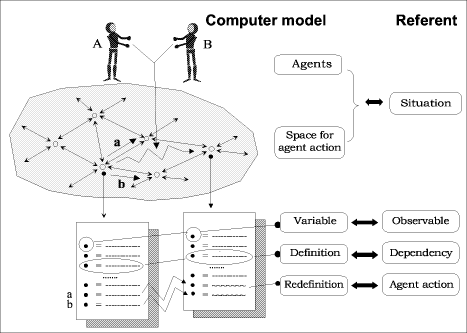
guard of a command (as with n Page 409 in a verified (if the conditions have been checked!) implementation of a heapsort algorithm valid for any finite heap. 3 Interpreting the formal developmentA development such as this is a standard example for classes in algorithm development and program verification. Experience shows that, from whichever way the development is approached (that is, either requiring students to formalise a heapsort process, or presenting the formalised version as a case study) understanding and interpreting the formal approach is not an easy task. It is often helpful to give specific examples, draw pictures, and encourage students to experiment. Even for users familiar with a formal notation, experience and exploration are needed to understand a required task and find an appropriate abstraction. The importance of experimentation and visualisation has been recognised in many contexts, for example with Tarski's World [Barwise and Etchemendy 1992] for learning logic. One purpose of a formal specification is to provide a clear and unambiguous statement of a desired system. It is intended that the specification should be interpreted in only one way by all who read it, thus providing a sound basis for review and continued development. Work by Loomes and Vintner suggests that misinterpretation of formal text is extremely common and that, even amongst experienced users, the understanding gained from reading a specification can differ widely [Loomes and Vintner 1996]. Certain logical constructions (implication being the main culprit) cause particular problems, and the process of abstraction can itself be a barrier to understanding (incorrect inferences were frequently drawn from a specification, but never from specific instances). Interestingly, there also seems to be scope for systematic misinterpretation, with a group of subjects independently agreeing on the same (incorrect!) interpretation of a formal statement. The formal specification had been used to confirm the subjects' expectations. In order to establish an association between experience and a formal concept as in the case of heapsort, we may well go through some of the illustrative steps mentioned above. We might show pictorially the structures involved, provide visualisation of the steps required or give a manual demonstration of a heapsort process. These may or may not be instances of the formal specification examples couched in other terms can help our understanding and cases which show when things do not work can be particularly useful. The link is that they are all informative experiences which contribute to our appreciation of the heapsort. Of course, some experiences may not be so helpful. Indeed, we may be misled by something which looks like heapsort but is not, or by leaping to unjustified generalisations from particular cases. Given the importance of experience, it may be useful to ask how we may categorise the relevant ones in a particular case. What experiences could be viewed as the counterparts of the specification? Also, what is the nature of the relationship between what is experienced and what is formalised? In one sense, formality constrains, in that it requires many features to be pinned down. On the other hand, abstraction is one of the most powerful aspects of formal specification in that it leads to generality. A particular instance of heapsort stands in much the same relation to a specification as a particular occurrence of twoness Page 410 (such as observing a pair of magpies) stands to the abstract number two. Foundational issues in modern computer science (and the "logicist debate" in particular) hinge upon whether or not the ontology of abstract concepts is framed in experiential terms [Beynon 1999]. In the spirit of Smith [CantwellSmith 1996], who rephrases Kronecker's famous dictum as "Man made the integers all the rest is the work of God", EM puts its fundamental emphasis on observation and experiment. This perspective is discussed in the next section. 4 What is heapsort an observational point of viewHow can we sustain the claim that understanding of the formal specification of an algorithm is rooted in experience? Creating experiences that can illuminate the interpretation of a formal specification of an algorithm is problematic in several respects. In illustrating the execution of any abstract algorithm, many forms of particularisation are involved. There are many possible choices of input; many possible computer implementations using different programming languages and platforms; ways to demonstrate an algorithm that involve manual execution or the use of special artefacts. A central concern in demonstrating any algorithm is the presentation of state to the human interpreter: the different states of the execution have to be made manifest through some form of embodiment, and those states that are vitally significant in the interpretation of the algorithm distinguished from those that are incidental. A particular illustration helps to emphasise the significance of such issues. In the case of heapsort, imagine that we had constructed a "Heapsort Machine": a mechanical device in the form of a jointed tree structure in which tokens of different weights are placed at the nodes, and the exchange of tokens attached to a parentchild node pair is effected by rotating an arm of the tree. Using this physical artefact as a visual aid, we could demonstrate the steps of the heapsort process manually, sorting the tokens by weight. The possible inputs for the Heapsort Machine would no doubt be tightly restricted by physical constraints. The number of input tokens and their possible weights would be bounded. To convince an observer that the process was effectively changing state according to the correct prescription it would be necessary to have a means of demonstrating how tokens were ordered by weight in any particular configuration of the machine. For instance, it might be possible to extract an arm of the tree structure, together with the tokens at each end, and place it on a balance. In this context, it would be essential to recognise that the activity associated with using the balance was not to be interpreted as part of the heapsort algorithm. The concrete idiosyncratic character of the Heapsort Machine, and the subtlety of the observational and experiential issues that surround its use, are selfevident. In practice, the interpretation of any particular instance of heapsorting activity, however it is implemented, involves similar considerations. The formal description of heapsort, transcending any specific experience, can be related to such particular instances only through a powerful process of extrapolation. The key element in this process of extrapolation is supplied by the human interpreter. Recognising an instance of an abstract algorithm is essentially concerned with projecting an explanatory account onto an observed activity an important theme to be elaborated throughout the paper. With specific reference to heapsort, the activity should visit certain abstract states [as prescribed by the Page 411 formal specification], and involve certain characteristic abstract actions [such as "consulting the data value at a certain node, and if this value is less then the value at another node, carrying out an exchange"]. This characterises an instance of heapsort as a phenomenon in which as it is construed by the human interpreter statechange is effected by a reliable stimulusresponse mechanism [such as a conventional computer, or human following prescribed rules faithfully] that is configured to react to specified stimuli in a specified way. The fact that this characterisation of heapsort activity directly invokes the human interpreter is crucial. It gives prominence to activities of an empirical nature that are not well represented in the conventional theory of computation. From a philosophical perspective that favours an empirical stance, explanation of phenomena is a matter of making judgements about experiences. It may be convenient to presume that an explanation is in some sense "absolutely correct", but it is more illuminating to regard it as a provisional hypothesis that is always subject to refutation by future experience. This demands a radical shift on perspective on phenomena that are potentially instances of heapsort, one that is particularly difficult to make when we seek to explain the execution of a conventional heapsort algorithm. Characteristic of this shift is the idea of being able to intervene in an openended manner, in much the way that an experimental scientist explores the implications of changing contexts and parameters. The process of construing a phenomena provides a fundamental and subtle connection between theoretical and empirical perspectives. As Gooding remarks ([Gooding 1990], p.88): "Construing may be thought of as a process of modelling phenomena while the conceptual necessities of theory are held at arms length." Nonetheless construing is an imaginative activity that, like a theory, can transcend the limitations imposed by the particular, provisional and subjective qualities of experience. This can be illustrated with reference to the issues of particularising heapsort cited above. When we see a heapsort program execute on a particular set of numbers, we construe the mechanisms that operate as depending upon these numbers in a specific way, and as independent of the number of numbers in some abstract sense. For instance, if the inputs happen to have decimal expansions of distinct lengths, the sorting is presumed to rely upon comparing their values and not their representations. 5 Empirical Modelling principles for construingOur previous discussion connects recognising and creating experiential counterparts for a formal specification with construing phenomena. The principles and tools of EM serve to address two closely related issues: How do we represent and communicate our explanatory models? and To what extent and by what means can we exploit computer support? The character of EM activity can be best motivated by referring to the way in which experimental scientists have documented their understanding of phenomena. David Gooding's research into the experimental methods of Faraday [Gooding 1990] gives an appropriate orientation. In his analysis of Faraday's evolving understanding of electromagnetic phenomena, Gooding refers to the essential rôle played by "objects and images which conveyed likely relationships between electricity, magnetism, wires and magnetised needles". Gooding introduces the term "construal" to describe such artefacts, and characterises them Page 412 in the following terms: "Construals are a means of interpreting unfamiliar experience and communicating one's trial interpretations. Construals are practical, situational and often concrete. They belong to the preverbal context of ostensive practices." ([Gooding 1990], p.22); "... a construal cannot be grasped independently of the exploratory behaviour that produces it or the ostensive practices whereby an observer tries to convey it." ([Gooding 1990], p.87). EM can be viewed as contributing to the science of construing in two complementary ways. On the one hand, it offers principles that can be used to frame explanatory accounts. On the other, it introduces new practical techniques and tools for constructing construals. Though EM is centrally concerned with construals that exploit computerbased technology, it also offers a broader perspective on modelling in general. EM principles link construing phenomena to identifying observables, dependency and agency. This is consistent with our everyday understanding of the world, with the way in which scientific investigation is conducted, and how we may aspire to analyse more complex processes, such as social and political activities. The term observable refers to a feature of a situation that is perceived to have identity and integrity. A dependency is a relationship amongst observables that expresses expectations about how the values of observables are indivisibly linked in change. An agent is an observable (generally identified with a family of primitive observables) that is deemed to be responsible for changes of state within the situation. As discussed in [Beynon 1998], these fundamental concepts have broad interpretation and application. Their use will be sketched here in connection with an account of heapsort. In this context, the construals to be constructed resemble the blackboard diagrams that a lecturer would revise and annotate in introducing heapsort. The top half of Figure 1 depicts the computerbased construal for heapsort that we have developed using Empirical Modelling. The status of Figure 1 as a computer model will be discussed in the next section. This section focuses on the abstract analysis of observables, dependencies and agency that informs the construal. The motivation for the construal is most easily understood from the perspective of a student who witnesses an expert performing the heapsort process on an array, and has no auxiliary visualisation to aid interpretation. In developing the construal, more than mere visualisation of the heap data structure is involved. Understanding heapsort demands heap observation and manipulation of a very specific kind. Careful inspection of Figure 1 highlights the fact that what is given visual embodiment is precisely what the heapsort expert attends to in interpreting the data structure and its application. For instance, relevant features are: the order relationships between values at parent and child node;, whether the heap condition holds at a node; and the index of the child node with the greater value. A brief account of the dependencies between such observables to be captured in the construal follows. A student of heapsort who inspects Figure 1 has first to understand the relationship between the disposition of elements in the array and the geometry of the associated tree. This can be expressed using a simple system of dependencies:
This simple dependency enables the student to study the relationship between array values and tree values empirically, through changing the values of array Page 413 Figure 1: An EM construal for heapsort Page 414 elements, and observing the effect on the tree. In the tree, the basic observables are nodes and edges that metaphorically represent array elements and order relations between array elements that are significant in determining whether the tree satisfies the heap condition. A richer level of observation involves examining the values that are associated with the nodes in the tree, and the nature of the order relationships (<, =, >). In deciding whether the tree is a heap, it is further necessary to consider whether the heap condition is satisfied at each node that is to say, is the value associated with a particular node at least as great as that associated with each of its children. To model observation of this nature via dependencies requires observables to represent the index and value of each node, to record the order relation that pertains on each edge of the tree, and to register whether the heap condition holds at each node. The index and value of a node are defined by explicit values, whilst the order relations and heap conditions have values that depend on these. For instance, for the node with index i, the heap condition would be defined by: HC[i] = (val[i] (subject to a suitable convention to deal with nodes with less than 2 children). Likewise, an order relation for the edge that joins the nodes indexed by i and 2*i is defined by: OR[i, 2 * i] = if (val[i] > val[2 * i]) then 1 else (if(val[i] < val[2 * i]) then (-1) else 0. In our EM modelling environment, additional dependencies can readily be introduced to establish suitable visual conventions for representing these abstract conditions. For instance, the label of a node and the edges between nodes can be coloured so as to reflect whether or not the heap condition is satisfied at a node, and to reflect the nature of the order relation associated with an edge: colour_of_label_at_node[i] = if HC[i] then
black else white This allows the user to experiment with the assignment of values to nodes, and register visually the status of just those observables that are significant in understanding the heap concept. For instance, Figure 1 represents a heap if and only if all the nodes of the tree are coloured black. Such a condition can be independently monitored by attaching another highlevel observable, defined by is_heap = HC[1] and HC[2] and HC[3] and ... and HC[7] The computer model developed in this way serves a similar function to the animation that a lecturer might conduct on a blackboard when explaining the basic heap concept. For instance, it can be used to demonstrate how the heap condition is affected by changing the value at a node, or exchanging the values at adjacent nodes. In giving an account of heapsort, more is required. The definition of the heap condition has to be refined to take account of restricting the heap to a segment of the array. For this purpose, the indices that define the endpoints of this segment are new observables to be referred to as first and last, and a new observable in_heap[i] introduced to determine whether each index i lies within the segment. The definition of the heap condition at node i can then be interactively revised Page 415 to the form: HC[i] = not in_heap[i]
or(
in_heap[i]
and ((not in_heap[2 * i]) or (in_heap[2 * i] and OR[i, 2 * i] - 0))
and ((not in_heap[2 * i + 1]) or (in_heap[2 * i + 1] and OR[i,2 * i + 1]
6 The semantics of EM computerbased construalsThe above discussion illustrates how the development of a construal proceeds in an exploratory manner. EM tools give computer support to this activity, enabling incremental and interactive extension, refinement and revision of a computer model. The semantic framework for this modelling activity is radically different from conventional computer programming. The key feature is that what is being construed (to be termed the referent of the construal) is itself subject to clarification and modification during the modelbuilding. Such fluidity and negotiation of meaning is possible because the modelling involves openended experimental interaction with the environment of the referent. For instance, in construing heapsort, the modelling activity has to embrace interactions associated with issues such as "what is a heap?" that are pertinent but not specific to heapsort. The aim of this section is to examine the semantics of EM construals more closely. For more details of the practical tools that can be used to construct construals such as Figure 1, see [Beynon 1998]. Key concepts in using EM principles to construct construals are depicted in Figure 2. The concepts that pertain to the referent, and to the external semantics of the computer model are displayed on the right of the diagram. The way in which these concepts are represented in and through the construction of the computer model is indicated on the left. In the above discussion of construing heapsort, the computer model is the construal, and the referent is heapsort. A relevant situation might be observation of a heapsort expert in action. The diagram is to be interpreted in the implicit context of the modeller's exploratory interaction with the computer model and its referent. The aim of this interaction is to create a model embodying relationships between observables, dependencies and agents congruent to those that the modeller projects onto the referent. The computer model provides perceptible counterparts for relationships that typically cannot be directly observed in the referent. The use of humanoid icons to depict agents is not intended to exclude impersonal or inanimate forms of agency, but to stress a key principle of EM. All agency is construed as similar to human agency. All statechanging agents are construed as operating through changing observables and, in their turn, responding to changes of observables. The current state of the referent, as construed by the modeller, is determined by the current values of the observables and the dependencies that hold between them. Each observable is represented by a variable in the computer model. To each variable there is an attached definition that resembles the definition of a spreadsheet cell in character. This definition may either associate an explicit value with a variable, or express the way in which its value is functionally dependent on the values of other variables. Page 416 Figure 2: Empirical Modelling for computerbased construals Taken in conjunction, the variable definitions in the computer model make up what we shall call a definitive (for definitionbased) script. It is significant that the definitions attached to variables are not fixed or subject to variation within a preconceived circumscribed framework. The values and dependencies exhibited by the computer model are subject to change in many different ways. Such changes are always driven by its rôle as a construal, but can have all kinds of semantic significance. For instance, redefining a variable may reflect a change of state in the referent, or a correction to an observation; introducing a new dependency may correspond to a new insight on the part of the modeller, or a development in the situation. (A useful comparison can be made here with a spreadsheet, whose possible evolution in development and use is similarly guided by its external semantics, so that its potentially meaningful states cannot be preconceived.) As befits its openended exploratory rôle, the computer model is associated with the uncharted space of possible configurations of values and dependencies that can be associated with a definitive script. Despite its openness, this characterisation is precise in much the same sense that the concept of mainland Britain represents the land most of which I have never visited which I can in principle reach on foot. As a pedestrian explorer, I cannot specify in advance what land can be reached. In clarifying my referent, I may need to negotiate interpretations: is an island reachable by lowtide, or on an inland lake part of Page 417 mainland Britain? How can I be absolutely sure that the Isle of Wight will never be accessible by foot? Is the American Embassy part of the British mainland? As Figure 2 indicates, my perception of a situation is represented both by the space of conceivable states of a definitive script, and by the statechanging agents that I construe to operate in that space. Agent action is associated with particular privileges to redefine variables. In Figure 2, possible actions of agents A and B are represented by the redefinitions and corresponding transitions in state space labelled by a and b respectively. Figure 2 depicts a and b as noninterfering actions that can be performed simultaneously to achieve the same state transition as would result from performing them in either order. This is represented in the computer model by performing redefinitions of a and b in parallel. 7 EM construals and formal specificationThe openness of a heapsort construal is respected in its implementation using EM tools. There is no single way in which the computer model can be extended and applied. In using definitive scripts to represent state, the ordering of definitions is immaterial. This means that the same script can be organised for presentation in different ways, and assembled in different orders. Two distinct purposes for a heapsort model derived from the experimental environment for studying the heap concept introduced above are discussed elsewhere [Beynon 1998, Beynon et al 1998]. Two models chosen from these sources to illustrate subtleties associated with construing an activity as heapsort will now be briefly outlined. The definitive script outlined in the previous section captures the way in which the values at the nodes of the tree, the order relations on the edges, and the heap conditions at the nodes depend upon the values in the array. By interacting with such a script, manipulating the values of first and last, and making appropriate sequences of exchanges, a user can manually simulate heapsort. The visualisation in the model is such that the choice of nodes at which to perform an exchange can be inferred from the colours encircling the nodes. This means that the user can learn to carry out heapsort without explicitly consulting the values at nodes, following a recipe based only upon the colour conventions used in their visualisation. Consideration of this model exposes some of the subtle issues attached to construing an activity as heapsort. A user who learned the colour conventions to be followed in a recipe for heapsort could not necessarily be deemed to be performing heapsort. Possible experiments to test understanding could easily be applied by adapting the heapsort model. Suppressing the colour coding on the visualisation, or removing the dependency between the visualisation and the true values at the tree nodes would both offer relevant insight. The use of EM tools also makes it possible to introduce automatic agents into models. In [Beynon 1998], a number of possible scenarios are described, in which different degrees of automatic support for heapsorting are offered, ranging from completely manual to completely automatic execution. All these models can be derived interactively from a single model simply by introducing an appropriate file of definitions and automatic agents. An automatic agent is represented by a triggered procedure for redefinition. A useful mechanism that is exploited in all Page 418 the automated models attaches such an agent to each node of the tree. When the heap condition at this node is violated, the corresponding agent is primed to exchange the value at this node for a value attached to one of its child nodes, whichever is the greater. An interesting feature of this approach that the heapsort process can be mimicked merely by manipulating the first and last indices according to the prescription of heapsort, followed by invocation of any primed agent attached to a node. Despite appearances, this process differs from authentic heapsort in a significant way. In effect, the transfer of control from node to node is always driven by the nodes at which the heap condition is currently violated. This does not accord with the formal specification, where for the most part transfer of control entails no reference to the values attached to nodes. In this case, the need to construe the activity as differing from heapsort is disclosed by intervening during the execution of the algorithm. A conventional heapsort does not repair violations of the heap condition except in contexts that are preconceived in designing the control procedure. Our unconventional algorithm in some circumstances can. Figure 1 is an extension of the heapsort model that includes observation that is associated with a formal specification of heapsort. The concept behind this extension is that the formal specification supplies an abstract trace of the heapsorting process as it might be observed by a mathematician. The lower component of Figure 1 takes on a different form according to which phase of the heapsort algorithm is currently being inspected, and the values of invariants and variants are monitored as the algorithm is executed. There are two complementary motivations for such observation: the formal specification can be used to confirm that the heapsorting process is indeed being correctly followed, or the heapsorting process may serve as worked example for the purpose of checking the accuracy of the formal specification. In Figure 1, the invariants and variants of the specification are treated as observables in their own right, and linked to the more primitive observables attached to the heapsort model. Strictly speaking, this mode of observation of the heapsort model is only appropriate in a restricted context for use, since it presumes that heapsorting activity is in progress, and makes references to observables concerned with control issues. For instance, each invariant is expressed as a predicate whose truth value is dependent on the current state, as determined by the present status of both data and control. As the above discussion has indicated, there are many modes of interaction with the heapsort model. Most of these operate outside the context of a particular heapsorting process. When monitoring the invariants of the formal specification in interaction with the model, the user has complete discretion over whether this interaction respects the heapsorting process. This is a crucial distinction between our computerbased construal and a conventional animation of heapsort. The function of a construal can only be served by a model that can be tested beyond the limits of any preconceived and circumscribed range of interactions. If our formal specification is flawed, it is still important that it can be incorporated in the model. If the heapsort process is not correctly followed, there must be scope to reflect this deviation. More generally, a complete understanding of the heapsort process if indeed there is such a thing stems from insight into the way in which the process relies upon its context. In developing this insight, it is valuable if not essential to have scope for experimental interaction. Setting algorithm specification and design in an experimental setting is a Page 419 powerful way to explore and develop new functionality. In experimenting with the model in Figure 1, we can "follow the right steps in the algorithm" and "check that the invariants are respected", or "deliberately depart from the algorithm" and "check that this transgression is reflected in the specification". It is appropriate to annotate these phrases with quotation marks because they may reflect the intentions of the human interpreter rather than the true status of the model: there may be unrecognised anomalies in either the specification or the construal. Observation of invariants and variants attached to the formal specification can also be used in a constructive way to counteract the effects of random changes to the values to be sorted during the heapsort process. To demonstrate, we have created a variant of the heapsort model in which such changes prompt the model to determine the optimal point to which the heapsort process has to be rewound. In this way, observation of the formal specification is used as a powerful form of metacontrol that would normally entail intelligent action on the part of a user. 8 ConclusionIncorporating a formal specification into an EM environment allows us to interpret the significance of the formal statements and to explore the concepts behind them. One aspect of the EM approach is the visualisation it provides but, as emphasised above, an observationoriented viewpoint offers more than this. Fundamental to the approach is its support for user interaction and experimentation which is crucial for gaining an understanding of the abstract concepts in a formal specification. To explore a particular algorithm effectively, the openness of interaction associated with EM may need to be restricted in certain ways (as when tracing the steps of the algorithm) but the user is also free to step outside such constraints for a wider exploration of the subject. Reliance on empirical evidence does not give certainty since, although experience can contribute to understanding, it can also be misleading. It is essential to introduce formal specification to guard against this. Combining the two helps us to formulate theories which can be verified. Our work emphasises the different and complementary nature of the two approaches, but also reveals some similarity. Both a formal specification of heapsort and a construal of a particular instance of heapsort refer to abstract features of a physical process that are independent of any particular realisation. Although the approach here has been to explore an existing specification from an observationoriented perspective, it would also be possible to start with an EM investigation to explore the requirements and clarify ideas, using this to inform the construction of the formal specification. Safetycritical areas, such as railway operation, have been successfully modelled both empirically [Beynon 1999] and formally [FMERail]. A combined approach may be beneficial here, with EM helping to resolve conflicting requirements and perhaps suggesting approaches which might not otherwise have been considered. The further development of existing EM tools to support such usage will be a theme of future work. The distributed variants of our EM tools are of particular interest in this connection. Page 420 References[Araki et al 1999] K.Araki, A.Galloway, K.Taguchi (eds). Proceedings of Integrated Formal Methods. Springer, York UK, June 1999. [Barwise and Etchemendy 1992] J. Barwise and J. Etchemendy. The language of firstorder logic (Third Edition) Center for the Study of Language and Information, Stanford, 1992. [Beynon 1998] W. M. Beynon. Modelling state in mind and machine. Research Report 337, Dept. of Computer Science, Univ. of Warwick, 1998. [Beynon et al 1998] M.Beynon, J.Rungrattanaubol, P.H.Sun,A.Wright. Explanatory Models for OpenEnded HumanComputer Interaction. Research Report 346, Dept. of Computer Science, Univ. of Warwick,1998. [Beynon 1999] M.Beynon. Empirical Modelling and the Foundations of Artificial Intelligence. Proceedings of Computation for Metaphors, Analogies and Agents, Lecture Notes in AI 1562, SpringerVerlag, 322364, 1999. Also available from http://link.springer.de/link/service/series/0558/tocs/t1562.htm [CantwellSmith 1996] B. CantwellSmith. The Origin of Objects. The MIT Press, 1996. [Dijkstra 1976] E.W. Dijkstra. A Discipline of Programming. Prentice Hall, 1976. [EM web] The Empirical Modelling website. http://www.dcs.warwick.ac.uk/modelling [FMERail] FMERail website. http://www.ifad.dk/Projects/fmerail.htm [Gooding 1990] D.Gooding. Experiment and the Making of Meaning Kluwer Academic Pubs., 1990. [Hoare and He 1998] C.A.R.Hoare and He.Jifeng. Unifying theories of programming. Prentice Hall, 1998. [Loomes and Vintner 1996] M.Loomes and R.Vinter. Formal Methods: No Cure for Faulty Reasoning. Technical Report 265, School of Information Sciences, Univ. of Hertfordshire,September 1996. Page 421 |
|||||||||||||||||||
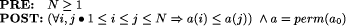
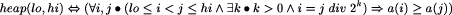
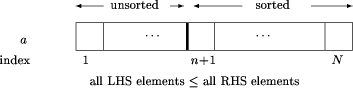
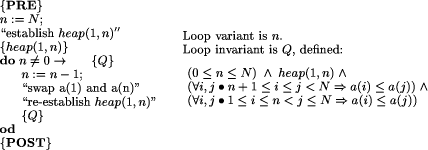
 0 in the plan) indicates when that command is enabled. A formal development
along these lines results
0 in the plan) indicates when that command is enabled. A formal development
along these lines results 
 val[2 * i]) and (val[i]
val[2 * i]) and (val[i]