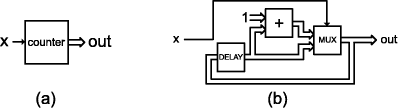
Implementation of an Embedded Hardware Description Language Using Haskell

Abstract: This paper describes an ongoing implementation of an embedded hardware description language (HDL) using Haskell as a host language. Traditionally, "functional" HDL's are made using lazy lists to model signals, so circuits are functions from lists of input values to lists of output values. We use another known approach for embedded languages, in which circuits are data structures rather than functions. This style of implementation permits one to inspect the structure of the circuit, allowing one to perform different interpretations for the same description. The approach we present can also be applied to other domain-specific embedded languages. We provide an elegant implementation of memories and a set of new signal types.

Key Words: domain-specific languages, embedded languages, hardware description

Categories: B.5.2, B.6.3, D.3.2, I.6.2

1 Introduction

Building a domain­specific language from scratch can be a long task because it consists of dealing with many issues like designing syntax, scoping, type and module systems, and developing tools like parsers, compilers or interpreters. The embedded approach is, indubitably, a good way to describe and to implement domain-specific languages. Building a domain-specific "library" on top of a convenient general-purpose language, one can get rid of many design decisions, because the infrastructure of the host language is inherited, avoiding most of the issues above. Some performance is lost, but often it is not so important. Benefits and drawbacks of the embedded approach are found in [Hudak, 1998].

Functional languages have some advantages that make them well-suited for the design of domain-specific languages: strong typing, pattern matching, higher-order programming (first class functions), laziness and parametric polymorphism are key features that make the design very elegant and modular.

We focus on the domain of hardware description, which is the area we are working on at the present time. We consider this area an excellent case study because it explores many features concerning the embedded approach and also because descriptions can be "interpreted" in several ways (e.g. they can be simulated, translated to other HDLs or input to verification tools).

We have chosen Haskell to develop our work because it encompasses several desired features as mentioned above. For instance, we highlight its strong type system that catches as many errors as possible at compile time, and type classes that provide concise and generic circuit descriptions. There are some publications that show a more detailed discussion about choosing Haskell as a host language. Some examples are [Elliott, 1999, Launchbury et al., 1999]. Haskell has been also used to embed several other domain-specific languages, including other hardware description languages.

Although we focus in Haskell and in the hardware description domain, this paper gives a general idea on how to embed languages into a lazy, strongly typed functional language.

A simplified version of the language that is being developed is presented. The reader is supposed to be familiar with the functional programming paradigm and with the Haskell framework. If it is not the case, see [Thompson, 1999] for an introduction to Haskell and [Hudak et al., 1992] for details.

1.1 Overview of the paper

First, we present some background in "functional" hardware description and motivation. Then, we show the difference between representing circuits as functions over lists and as data structures and explain why we have chosen the second option. Further, we show the implementation of the language and discuss about important subtles and why we prefer some decisions. Then, we cite related work and, finally, we present conclusions and future work.

2 Background and Motivation

Before we start showing the implementation of our hardware description language, let us outline a brief background in "functional" hardware description.

2.1 A simple sequential circuit

Consider the simple circuit in figure 1, where (a) shows the circuit as a black box and (b) shows it from the inside. This is a "high­level" diagram of a simple counter circuit with an input bit and a vector of bits as output, representing an integer number. It is controlled by a clock signal that is not represented in the diagram. Its meaning is: in the ith clock tick, if the input bit x is False, the output number is the same as the output number in the clock tick i­1. If x is True the output is increased by one.

Thus, if the circuit receives the sequence [False, False, True, False, True, True] as input, it outputs the sequence of values [0, 0, 1, 1, 2, 3]. The MUX component is the same as an if­else­then function, + is the plus operation, and DELAY is an inherent sequential component that outputs its input value in the i­1th clock tick and, in case of the first clock tick, it outputs a given initial value as we shall see.

In the "functional" style of hardware description, the circuit in figure 1 would be described as a code like that of figure 2. Every circuit is represented by a function.

          countWhen :: Signal Bool ­> Signal Word8 
          countWhen x = out 
            where 
              out = mux x aux1 aux2 
              aux1 = delay 0 out 
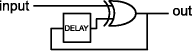
              aux2 = plus (constant 1) aux1

A Signal models a wire in a circuit (or vector of wires - that is why the syntax of signal types is Signal XXX, where XXX says what kind of signal it is). As we are using Haskell, the first line is the function interface, which means that the circuit has a boolean signal as input and a word signal of eight bits as output. The next lines are the definition of the function (we like the clarity of the where construction). In the definition, we have to describe what each signal is. As the reader can see, if the designer has the diagram of the circuit, the description is straightforward. Note that delay receives an initial value 0 and an input value out. We are assuming that the definitions of mux, delay and plus are already provided by the basic library of the language. If there are some sub­circuits that are not provided by the basic library, they simply must be implemented as other functions.

2.2 Implementing a very simple language

A possible implementation of a very simple embedded language that permits describing the above counter is the library in figure 3 (note: we have already described the xor2 combinator because we will use it soon).

          import Word 

          type Signal a = [a] 

          constant :: a ­> Signal a 
          constant = repeat 

          plus :: Num a => Signal a ­> 
                  Signal a ­> Signal a 
          plus xs ys = zipWith (+) xs ys 

          mux :: Signal Bool ­> Signal a ­> 
                 Signal a ­> Signal a 

          mux xs as bs = zipWith3 f xs as bs
            where f x a b = if x then b else a 

          delay :: a ­> Signal a ­> Signal a 
          delay x ys = x:ys 

          xor2 :: Signal Bool ­> Signal Bool ­>
                  Signal Bool 
          xor2 xs ys = zipWith (/=) xs ys 

Typically, such a library is composed by an abstract datatype (Signal a in this case), and combinators (plus, constant, mux, etc.) to produce larger sentences of the language. If we load this code together with the countWhen definition in a Haskell interpreter and run the command

Main> countWhen [False,False,True,False,True,True]

it will produce the result

[0,0,1,1,2,3]

as we expected. Often tools are implemented for interpreting the sentences, but in this example it is not the case, because circuits are Haskell functions. As we shall see, when implementing circuits as data structures, it will be necessary to implement interpretation functions because data structures are not naturally executable.

Another example is the circuit toggle in figure 4, composed by a xor2 component (the xor operation) and a delay. Its meaning is: For the ith clock tick (i > 1), if the ith input value is high, then the ith output value is the i - 1th output value inverted, else the ith output value is the same i - 1th value. The first output value is equal to the first input value.

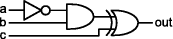
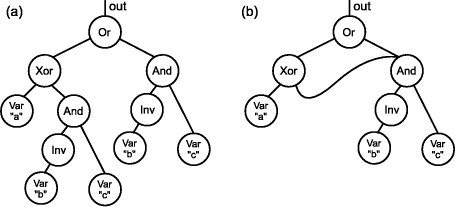
toggle :: Signal Bool ­> Signal Bool toggle input = out where out = xor2 input aux aux = delay False out

Note that the definitions of the signals out and aux are mutually dependent. It is not a problem because of the lazy execution of Haskell and the initial value provided by the delay component. A mutually dependent definition without any delay would lead to an error (and smoke in a real circuit).

As we have mentioned, there is not explicit clock representation. It is a particular subtle in the "functional" style of hardware description: the notion of clock is implicitly carried by the position in the sequence of values (usually represented as ordinary lists). Thus, low­level details about timing are not considered: the simulation tools assume that the clock period is long enough to update all the internal component outputs. The careful reader probably has realized that "functional" HDL's fits well for signal processing, microarchitectures and the like.

2.3 Functions on lists vs. Data structures

In the previous subsection, we outlined an implementation of a simple embedded hardware description language as a library in which signals are modeled as lists and circuits are Haskell functions from lists to lists. With this implementation we can not do much more than simulate the circuits. We can not access the internal structure of the function to see how it was built.

Therefore, we want to implement the circuits in such a way that we can inspect its internal structure and perform different interpretations like simulation, verification, translating to other languages and so on.

In figure 5 we sketch a simple implementation in which circuits are represented by a data structure (in this case, a tree). We are considering only boolean signals for now. Now the basic combinators are signal expression builders and the circuits are nothing more than bigger expressions.

     data Signal                 low = Bool False
       = Bool Bool               high = Bool True
       | Var String              var x = Var x 
       | Inv Signal 
       | Xor Signal Signal       inv x = Inv x
       | And Signal Signal       xor2 x y = Xor x y
       | Or Signal Signal        and2 x y = And x y
       | Delay Bool Signal       or2 x y = Or x y
       deriving Show             delay x y = Delay x y

With this basic library, the style of descriptions remains the same, as we can see in the arbitrary example in figure 6. The functions low and high are primitive combinators to build "boolean leaves" in the tree.

circ1 a b c = out where out = xor2 aux1 c aux1 = and2 (inv a) b

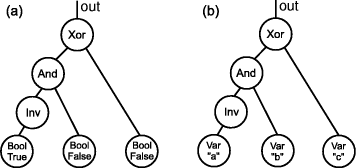
The var combinator takes a string and builds a symbolic leaf in the tree (symbolic values are useful for performing interpretations like verification and translation to other languages). Figure 7 shows two examples of trees built from the circuit definition in figure 6. The first tree represents the circuit in some given boolean signals and the second represents the circuit in symbolic values. These expression trees now must be interpreted. Evaluating (or simulating) the expression represented by the tree in figure 7 (a) does not seem to be a complex task - a simple recursive traversing algorithm could do it.

   (a)      Main> circ1 high low low 
         Xor (And (Inv (Bool True)) (Bool False)) (Bool False) 
   (b)      Main> circ1 (var "a") (var "b") (var "c") 
         Xor (And (Inv (Var "a")) (Var "b")) (Var "c") 

Also, suppose we want to traverse the tree in figure 7 (b) and generate code for the VHDL language. It would be carried out in a similar way.

However, the language presented is very poor because it cannot deal with primordial issues that must be treated. In the rest of the paper we show this issues and the solutions to solve them.

3 Implementation

3.1 Back to the parametric signal type

For performance and resource issues, we would like to abstract not only a single wire as a signal. We would like to represent a vector of eight bits as a signal of type Word8, a vector of sixteen bits as a signal of type Word16 and so on. Thus, we would like to come back to the parametric signal type Signal a.

To do this, we use the approach shown in [Leijen and Meijer, 2000]: we define an expression type Node encompassing all types and basic gates. Then, to prevent building incorrect sentences (e.g. Xor (Bool False) (Word8 27)) we define a layer of type safety (a phantom type) and build basic combinators respecting the signals types, as shown in figure 8 (data type) and figure 9 (some basic functions).

It is vital to provide function signatures in order to obtain type safety. As an example, if there was not a signature in the xor2 function, its type would be

               data Node 
                 = Var String 
                 | Bool Bool 
                 | Word8 Word8 
                 | Word16 Word16 
                 | Inv Node 
                 | Xor Node Node 
                 | And Node Node 
                 | Or Node Node 
                 | Plus Node Node 
                 | Mux Node Node Node 
                 | DelayB Bool Node 
                 | DelayW8 Word8 Node 
                 | DelayW16 Word16 Node 

              newtype Signal a 
                 = Signal Node 

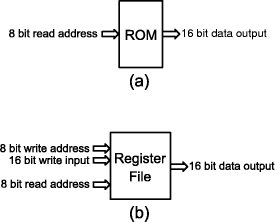
Signal a ­> Signal b ­> Signal c.

To save space, only a few combinators are shown in figure 9. Further we will implement some polymorphic combinators, like mux, var and plus. For now, we are assuming there is only a specific function for each type of signal: muxB is a multiplexor on single bits, muxW8 is a multiplexor on vectors of eight bits and so on. The same occurs for var, plus and delay.

3.2 Detecting sharing

Let us consider the circuit in figure 10. As one can see, the result signal from the and gate is shared by the xor and the or gates. With the present implementation of the language, there is no way of building a traversing function that can detect such sharing. If one runs any traversing function for circ2 (varB "a") (varB "b") (varB "c"), such function would "understand'' this sentence as a tree with redundant branches, as in Figure 11 (a). It would be worse if we call it for the toggle circuit in figure 4 because it would lead to an infinite tree! What we would like to get is a graph as in figure 11 (b).

To avoid performing redundant computations or incurring in an infinite loop, it would be necessary to give a unique tag to each node and also perform a convenient traversal algorithm on the new structure. In functional programming, it is very diffcult to represent graphs with sharing without adding impure features.

          low :: Signal Bool 
          low = Signal (Bool False) 

          w8 :: Word8 ­> Signal Word8 
          w8 x = Signal (Word8 x) 

          xor2 :: Signal Bool ­> Signal Bool ­> Signal Bool 
          xor2 (Signal x) (Signal y) = Signal (Xor x y) 

          muxW8 :: Signal Bool ­> Signal Word8 ­> 
                   Signal Word8 ­> Signal Word8 
          muxW8 (Signal c) (Signal x) (Signal y) 
            = Signal (Mux c x y)

          delayB :: Bool ­> Signal Bool ­> Signal Bool 
          delayB x (Signal y) = Signal (DelayB x y) 

circ2 a b c = out where out = or2 aux1 aux2 aux1 = xor2 a aux2 aux2 = and2 (inv b) c

In [Claessen and Sands, 1999], Claessen and Sands show some previous solutions and propose to solve this problem extending Haskell with reference types. The big advantage is that this technique keeps the clear and sweet style of description, without explicit naming or any other changes for the designer point of view. The major disadvantage of this technique is that it uses an impure mechanism to give unique names to the nodes, which loses referential transparency.

A referenced object of type Ref a is an object of type a ``packed'' together with an implicit unique tag. To build a reference type, there exists the function ref :: a -> Ref a. To ``unpack'' a reference type, there exists the function deref :: Ref a -> a. To compare if two references are the same, there exists the infix operator (<=>) :: Ref a -> Ref a -> Bool.

The final implementation of the signal type and some basic combinators are given in figure 12 (the data type) and figure 13 (some basic functions). The implementation of the Ref module can be found in [Claessen, 2001].

A new type Graph was created to not clutter up the definition of the Node type. The Node type defines all basic gates and end values that can appear in a circuit description and the Graph type adds recursion and references.

3.3 The BitVect class

We have implemented a BitVect type class to provide polymorphic combinators over different signal types (figure 14). We have implemented instances for Signal Bool, Signal Word8, etc. With this class, for example, any kind of multi-plexor (on single bits, on vectors of eight bits, etc.), are represented by a function called mux. The same occurs for other combinators belonging to the class. The dff combinator is a circuit equivalent to a delay initialized with zero. We could not include delay in this class because of the fact that its initial value would have to be different for each instance.

With this class one can declare polymorphic circuits. Consider the above counter again. Now we can describe the same counter for any signal type as shown in figure 15. The type of the counter is now BitVect a => Signal Bool -> a. The Haskell type inference system is responsible for matching the correct instance class, depending on where the counter is inserted.

3.4 Overloading tuples and lists of signals

Often, a circuit output contains more than one signal. In this case, they must be grouped in a tuple or list or a combination of them (because functions return only one value). Also, for overloading issues, we do the same (grouping in tuples and lists) for input values, as we have already done in figure 13. As a example, a halfAdd circuit that receives two bits and returns their sum and carry bit would have the signature halfAdd :: (Signal Bool, Signal Bool) -> (Signal Bool, Signal Bool).

                     import Word 
                     import Ref 

                     data Node a 
                       = Bool Bool 
                       | Word8 Word8 
                       | Word16 Word16 
                       | Var String 
                       | Inv a 
                       | Xor a a 
                       | And a a 
                       | Or a a 
                       | Plus a a 
                       | Mux a a a 
                       | DelayB   Bool   a 
                       | DelayW8  Word8  a 
                       | DelayW16 Word16 a 

                     newtype Graph
                       = G (Ref (Node Graph)) 

                     newtype Signal a 
                       = Signal Graph 

Why have we grouped inputs and outputs together? Because we want to provide generic interpretation functions for the descriptions.

To help overloading tuples and lists of signals, we have implemented a Struct type and a Generic type class the same way in [Claessen, 2001] (figure 16). We created Gen instances for (), Signal a, Gen a => [a], (Gen a, Gen b) => (a, b) and so on. Thus, every time we have to deal with a Generic type, we convert it to an object of type Struct Graph (using to), traverse it for every single value, then convert it again to the Generic type (using from).

Thus, a simulating function that receives a circuit and a list of inputs and returns a list of outputs would have the signature: sim :: (Gen a, Gen b) => (a -> b) -> [a] > [b].

3.5 Memories

We have implemented memories in a similar way we have implemented delay: defining the initial value and input values. Suppose our language provides a read-only memory with 8-bit address and 16-bit values (figure 17 (a)), and a register file (note: we give a example of a simple register file, which writes a word and reads a word per cycle) with an 8­bit address, 16­bit values (figure 17 (b)).

     low :: Signal Bool 
     low = Signal (G (ref (Bool False))) 

     varB :: String ­> Signal Bool 
     varB x = Signal (G (ref (Var x))) 

     xor2 :: (Signal Bool, Signal Bool) ­> Signal Bool 
     xor2 (Signal x, Signal y) = Signal (G (ref (Xor x y))) 

     muxW8 :: (Signal Bool, (Signal Word8, Signal Word8))
              ­> Signal Word8 
     muxW8 (Signal c, (Signal x, Signal y)) 
       = Signal (G (ref (Mux c x y))) 

     delayW8 :: Word8 ­> Signal Word8 ­> Signal Word8 
     delayW8 x (Signal b) 
       = Signal (G (ref (DelayW8 x b))) 

We put a new option in the Node type for each kind of memory the language will support and create basic combinators to build them (see figure 18). Although it seems quite simple to implement memories, the real work is in their simulation, where we use mutable arrays for better performance and to save resources.

3.6 Interpretation tools

Suppose we have defined some circuit and want to simulate it. We have to implement a function that receives the circuit, a list of input values and then examines the graph corresponding to the circuit, evaluating it for each input value. We use the ST monad [Launchbury and Jones, 1995] because we want to perform destructive updates in the simulation.

As we have already mentioned, the simulation function has the signature: sim :: (Gen a, Gen b) => (a > b) > [a] > [b].

First, we traverse the circuit structure, converting reference types to ``real'' pointer references (mutable variables), using the function toSTRefs, which type is Struct Graph -> ST s (Struct (STS s)), where the STS s type is described in figure 19. This function traverses the circuit data structure keeping track of the sharing information and builds another data structure on top of the STS s type.

            class BitVect a where 
              zero :: a 
              one :: a 
              var :: String ­> a 
              plus :: (a,a) ­> a 
              dff :: a ­> a 
              mux :: (Signal Bool,(a,a)) ­> a 

            instance BitVect (Signal Word8) where 
              zero = w8 0 
              one = w8 1 
              var = varW8
              plus = plusW8 
              dff = delayW8 0 
              mux = muxW8 

             countWhen x = out 
               where 
                 out = mux (x, (aux1, aux2))
                 aux1 = dff out 
                 aux2 = plus (one, aux1) 

The STS s type defines all possible kinds of pointer references that might appear. The first kind (with the STT constructor) belongs to trivial gates (without internal state), the following three types belongs to delay components and the last to memories. Note that all types are ST references to tuples. In all cases, the first element is a recursive Node - that is exactly what we want to do because we are building another graph with ST references instead of Ref references. The second element is the present value of the Node in the simulation. For stateful components, there is a third element of the type of their internal state, that will be updated whenever necessary.

Further, we run a stateful algorithm to simulate the circuit, updating internal states and calculating output values. For performing other interpretations, a similar approach must be taken. For generating VHDL code, for example, its necessary to give a symbolic input to the circuit and perform a traversal algorithm that generates the corresponding string code depending on what each node is. We have not done it yet because we are still studying VHDL subset needed to represent our circuit elements.

   data Struct a           class Gen a where
    = Single a               to :: a ­> Struct Graph
    | Compound [Struct a]    from :: Struct Graph ­> a

4 Related Work

Embedding a domain­specific language into Haskell has been an interesting topic of research nowadays. Haskell has been successfully used to embed several applications such as 2D and 3D animation [Elliott, 1999], music [Hudak et al., 1996], SQL queries [Leijen and Meijer, 2000] and others.

Johnson's work ``Synthesis of Digital Designs from Recursion Equations'' [Johnson, 1984] and Sheeran's [Sheeran, 1983] ``µFP, an algebraic VLSI design language'' have inspired many efforts in representing circuits by the functional­like style of description. Below, we cite the main works that have influenced our research:

The Hydra system [O'Donnell, 1996], developed by O'Donnell, consists of a set of methods and software tools for circuit design. It was previously built on top of the functional languages Daisy, Scheme and LML. Hydra provides some high­order combining forms and circuits are implemented as functions on stream values.

     data Node a 
      = Bool Bool 
      | Word8 Word8 
      | Word16 Word16 
      | Var String 
      | Inv a 
      | Xor a a 

      ... 
      
      | RomW8xW16 [Word16] a 
      | RegFileW8xW16 [Word16] a a a 

     rom8x16 :: [Word16] ­> Signal Word8 
                ­> Signal Word16 
     rom8x16 ws (Signal x) 
       = Signal (G (ref (RomW8xW16 ws x))) 


     regFile :: [Word16] 
                ­> ((Signal Word8, Signal Word16), 
                          Signal Word8) 
                ­> Signal Word16 
     regFile ws ((Signal a,Signal w),Signal r) 
       = Signal (G (ref (RegFileW8xW16 ws a w r))) 

One of Hydra's strengths is simulation, and it has been used to teach computer architecture at undergraduate level at University of Glasgow.

Hawk [Matthews et al., 1998] is an embedded language for describing modern microarchitectures. The aim of Hawk is to provide clear and concise micro­processors specification (to achieve this, Hawk has a rich library of superscalar microprocessor elements and provides behavioral descriptions using lifting and concepts like transactions). Hawk permits one to perform simulation, verification and algebraic simplification. As far as we know, Hawk doesn't make VLSI synthesis or netlist generation.

Lava [Bjesse et al., 1998, Claessen, 2001], created by Bjesse, Claessen, Sheeran and Singh, provides a set of tools, which can perform interesting circuit interpretations, like simulation, verification and VHDL code generation for FPGA implementation. Like Hydra, Lava provides high­order combining forms.

     data STS s 
       = STT       (STRef s (Node (STS s), 
                   Node Graph)) 
       | STDB      (STRef s (Node (STS s), 
                   Node Graph, STRef s Bool)) 
       | STDW8     (STRef s (Node (STS s), 
                   Node Graph, STRef s Word8)) 
       | STDW16    (STRef s (Node (STS s), 
                   Node Graph, STRef s Word16)) 
       | STMW8xW16 (STRef s (Node (STS s), 
             Node  Graph, STArray s Word8 Word16)) 

We have been highly inspired by the Lava system, mainly by its signal representation and overloading tuples and lists [Claessen, 2001]. This work differs from Lava because (a) we provide other high­level gates for the descriptions (memories for example), (b) we are implementing our own interpretations for the descriptions and (c) we are making our own implementation for some aspects of the core of the language like (c.1) implementing delay differently (in Lava, the initial value of delay is a generic signal, but we implement it as a specific constant) and (c.2) providing several types of word signals (as far as we know, Lava provides only Signal Bool and Signal Int) and overloads them on some operations.

5 Conclusions and future work

We have embedded a domain­specific language for synchronous circuit design. We show that this implementation leads to a clear and concise style of description to the language user, and also to a reduced number of function names because of the type polymorphism. Much of the Haskell infrastructure like module system, reporting errors, syntax and scoping are inherited to the embedded language, which makes the language design time very much reduced. In few hours one can declare initial definitions and see the circuits running. It certainly could take a long time if designing the language from scratch. Our first contribution was to summarize in one paper all the crucial aspects of an implementation of an embedded language for hardware description.

We also contribute with a gentle way of representing memories, where the initial values of a ROM or a RAM are represented by a Haskell list and further executed as a lazy state array. This representation put together the facility of just declaring a list in a Haskell module, and the desirable destructive update (in the case, of course) execution by demand.

We are currently working on the interpretations of the descriptions. We traverse the data structure of the circuit calculating result values or reporting errors. We are studying the subset of VHDL and Verilog languages (the most widely used HDL's) for translating our descriptions into them. As we have mentioned, we already know the technique of translation, but we must know all the syntax needed to represent our circuit elements.

Also, we are exploring ways of implementing new computer architecture elements like shared buses. We have encountered some problems in our first implementation of shared buses, but we believe that it is not a big problem because we have implemented them in an alternative way (with circuits as functions on lazy lists) and they worked perfectly. They must be treated differently from other components because of the special semantics of the three state buffers.

We expect to apply optimizations on the descriptions using some techniques presented in [Elliott et al., 2000]. We also could think about increasing the performance using the strict state monad, but we would lose many desired features, specially working with infinite lists. If we used strict monad, it could not be performed:

Main> sim countWhen (repeat high)

Another future direction is to apply our descriptions to formal methods. The data structure of our descriptions is well suited and ready to apply verification algorithms. Lava and Hawk have already been used as verification tools, performing operations like testing properties, algebraic reasoning and theorem proving. We hope to apply operations like those in our circuit elements too.

References

[Bjesse et al., 1998] Bjesse, P., Claessen, K., Sheeran, M., and Singh, S. (1998). Lava - hardware design in Haskell. In International Conference on Functional Programming. ACM SigPlan.

[Claessen, 2001] Claessen, K. (2001). Embedded Languages for Describing and Verifying Hardware. PhD thesis, Chalmers University of Technology and G˜oteborg University, G&oUML;teborg, Sweden.

[Claessen and Sands, 1999] Claessen, K. and Sands, D. (1999). Observable sharing for functional circuit description. In Thiagarajan, P. S. and Yap, R., editors, Advances in Computing Science ASIAN'99; 5th Asian Computing Science Conference, volume 1742 of Lecture Notes in Computer Science. Springer Verlag.

[Elliott, 1999] Elliott, C. (1999). An embedded modeling language approach to interactive 3D and multimedia animation. IEEE Transactions on Software Engineering, 25(3).

[Elliott et al., 2000] Elliott, C., Finne, S., and de Moor, O. (2000). Compiling embedded languages. In Workshop on Semantics, Applications and Implementation of Program Generation.

[Hudak, 1998] Hudak, P. (1998). Modular domain specific languages and tools. In Devanbu, P. and Poulin, J., editors, Proceedings: Fifth International Conference on Software Reuse. IEEE Computer Society Press.

[Hudak et al., 1996] Hudak, P., Makucevich, T., Gadde, S., and Whong, B. (1996). Haskore music notation - an algebra of music. Journal of Functional Programming, 6(3).

[Hudak et al., 1992] Hudak et al., P. (1992). Report on the programming language Haskell, a non-strict, purely functional language, version 1.2. ACM SIGPLAN Notices, 27(5). See http://www.haskell.org/definition for latest version.

[Johnson, 1984] Johnson, S. (1984). Synthesis of Digital Designs from Recursion Equations. The ACM Distinguished Dissertations Series, The MIT Press.

[Launchbury and Jones, 1995] Launchbury, J. and Jones, S. P. (1995). State in haskell. Lisp and Symbolic Computation, 8(4).

[Launchbury et al., 1999] Launchbury, J., Lewis, J. R., and Cook, B. (1999). On embedding a microarchitectural design language within Haskell. In Proceedings of the fourth ACM SIGPLAN International Conference on Functional Programming. ACM Press.

[Leijen and Meijer, 2000] Leijen, D. and Meijer, E. (2000). Domain specific embedded compilers. In 2nd USENIX Conference on Domain-Specific Languages, volume 35 of ACM SIGPLAN Notices. ACM Press.

[Matthews et al., 1998] Matthews, J., Cook, B., and Launchbury, J. (1998). Microprocessor specication in Hawk. In IEEE International Conference on Computer Languages, Chicago, Illinois. IEEE Computer Society Press.

[O'Donnell, 1996] O'Donnell, J. (1996). From transistors to computer architecture: Teaching functional circuit specification in Hydra. In Functional Programming Languages in Education, volume 1125 of Lecture Notes in Computer Science. Springer Verlag.

[Sheeran, 1983] Sheeran, M. (1983). µFP, an algebraic VLSI design language. PhD thesis, Programming Research Group, Oxford University.

[Thompson, 1999] Thompson, S. (1999). The Craft of Functional Programming. Addison Wesley, 2nd edition.