| Submission Procedure |
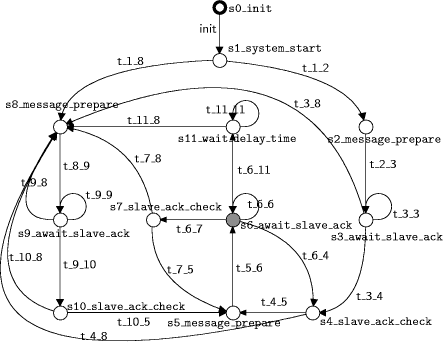
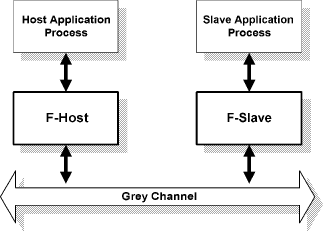
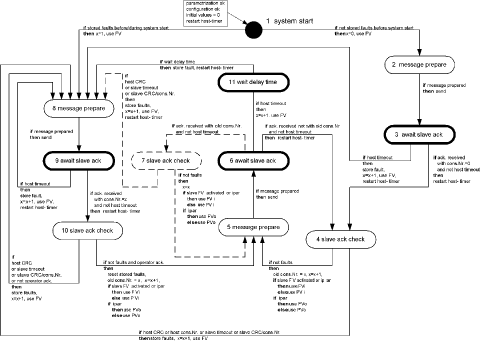
A Case Study in Verification of UML Statecharts: the PROFIsafe ProtocolR. Malik R. Mühlfeld Abstract: We discuss our experience obtained during the PROFIsafe verification and test case generation project at Siemens Corporate Technology. In this project, a formal analysis of the PROFIsafe protocol for failsafe communication has been carried out. A formal model based on finite-state machines has been obtained from the UML specification of the protocol. This model has been analysed with formal verification techniques, and several important properties have been proven. Based on the verified model, a set of test cases for the automatic execution of conformance tests has been derived. The paper explains how the UML statecharts difining the PROFIsafe protocol are translated into finite-state machines, and points out important aspects and problems occurring during the modelling and verification of industrial applications. Key Words: Reliability, verification. Categories: C.2.2 [Computer-Communication Networks]: Network Protocols-protocol verification; D.2.2 [Software Engineering]: Design Tools and Techniques-state diagrams; D.2.4 [Software Engineering]: Software/Program verification-model checking. 1 IntroductionIn this paper, we discuss the verification and test case generation of the industrial field bus protocol PROFIsafe [10]. This protocol has been analysed in a project at Siemens Corporate Technology, using the VALID Toolset as a model checking environment. A preliminary report on the project has been presented in [8]. The PROFIsafe protocol, which is used for failsafe communication in industrial field bus systems, must provide a very high level of reliability. Therefore, several measures are taken in order to ensure the correctness of the protocol specification. The formal analysis using model checking is one of these measures. As another measure, a certified testing environment is being set up in order to ascertain that implementations of the protocol conform to the verified specification. The behaviour of the PROFIsafe protocol is specified by means of UML state-charts. Its verification therefore leads to the general problem of verifying UML statecharts, which has been addressed by several other researchers [6, 7, 12]. Page 138 For example, [6, 12] describe a translation of general UML statecharts into PROMELA for verification by the SPIN model checker [5]. In contrast, the specifications to be verified in our project use only a small subset of UML statecharts. This does not only enable us to use a simpler translation procedure; it also avoids several ambiguities encountered when dealing with general UML statecharts. This paper is organised as follows. In Section 2, we introduce the PROFIsafe specification and the statecharts used. Afterwards, in Section 3, we discuss the abstraction steps needed in order to obtain a formal model of the protocol. In Section 4, we describe the translation process used to transform the UML statecharts into the finite-state machines used by the model checker. In Section 5, we explain which properties of the protocol were verified and present some of the results. In Section 6, we show how test cases were generated from the verified protocol. Finally, Section 7 contains some concluding remarks. 2 The PROFIsafe ProtocolThe PROFIsafe protocol [10] is used for failsafe communication between two agents using an insecure communication medium. The aim of failsafe communication is to ensure that two communication partners always enter a defined safe state in the event of any communication failure. This is important in many technical systems for which a high level of safety is required. Although originally defined as an extension of the PROFIBUS field bus protocol [4], the PROFIsafe protocol can be used to establish failsafe communication based on any underlying communication medium. Independently of the communication medium, it is designed to ensure a maximum error rate of one unnoticed fault in 109 hours of operation [10]. The protocol defines communication between two distinguished communication partners, called host and slave, who exchange messages via the underlying communication medium, called grey channel (Figure 1). The host usually runs on a controlling computer, while the slave typically runs on a technical device which is controlled by the host. Two kinds of slaves are considered: an input slave represents a field device collecting data, e.g. a sensor, whereas an output slave merely consumes data received from the host. The protocol specification makes no assumptions about the grey channel, which may produce all kinds of communication failures, such as delay, modifiqcation, duplication, or loss of messages. However, in most practical applications, such errors are assumed to occur only sparsely. The objective of PROFIsafe is to detect these sparse failures, should they occur, and to switch host and slave to their defined safe states before the fault can cause any harm. The PROFIsafe profile [10] defines a new layer of failsafe communication by specifying two new components called F-host and F-slave. Page 139 Figure 1: PROFIsafe architecture. The `F' in F-hostand F-slave is used throughout the PROFIsafe profile to identify the `failsafe' components introduced. These components use the grey channel as an underlying communication medium, and provide a means of failsafe communication to their users, represented by the application processes of the host and slave (Figure 1). The basic idea of the protocol consists of sending acknowledgements and monitoring live signs in the form of consecutive numbers in combination with timers. To this end, the PROFIsafe profile defines the following additional information to be put into all messages sent via the insecure grey channel. Consecutive number. Each message is equipped with a consecutive number, which is used by the recipient for monitoring the life of the sender and the communication link. Both communication partners continuously check whether the other partner manages to update the consecutive number before a defined watchdog time has elapsed. Eight bits are reserved for the consecutive number. The value 0 is used only for the first protocol cycle. Afterwards, the consecutive number runs in cyclic mode from 1. . . 255, wrapping over back to 1 at the end. CRC2 checksum. Each message is equipped with an additional CRC check-sum. This checksum is used to detect spurious or corrupted messages, which may have slipped unnoticed through the grey channel. Status byte. Each message sent from the F-slave to the F-host contains an additional status byte, with individual bits reserved for the different possible faults. In this way, the F-slave informs the F-host that it has detected a certain error, e.g. a CRC fault. Page 140 Figure 2: The statechart difining the behaviour of the PROFIsafe F-host. The PROFIsafe profile [10] describes the behaviour of the PROFIsafe F-host and F-slave by means of UML statecharts. As an example, Figure 2 shows the statechart difining the behaviour of the PROFIsafe F-host. The statecharts used here are very simple, exploiting only few features of the rich statecharts language provided by UML [9]. For example, there is no state hierarchy, and there are no entry, exit, or internal actions associated to states. In this way, the model remains very clear and avoids the ambiguities related to advanced features of UML statecharts [6, 12]. Also, the developers of this specification can be very sure that it will be interpreted in the same way by different readers and UML tools. Activity states, in which a communication partner is waiting for new messages to arrive, are highlighted in the PROFIsafe state diagrams (Figure 2). In this way, the synchronisation constraints are made explicit. 3 Creating a Formal ModelIn order to verify the protocol specification, a rigorous formal model needs to be extracted from the statecharts. Most of the transitions in the statecharts (Figure 2) contain verbal descriptions, which still require interpretation by a human. Page 141 Therefore, the first step involves adding the formal details which are missing in the semi-formal guards and actions labelling the transitions. We also need to abstract from some of the data used by the protocol, and we need to introduce a simple description of the behaviour of the grey channel. These tasks are not only needed in order to cope with the complexity of the model, but also to obtain a meaningful verification model at all. We use the following data abstractions.
In order to perform formal verification, it also is essential to formalise the behaviour of the environment in which the system to be verified runs, i.e. the grey channel. The behaviour of the grey channel is described verbally in the PROFIsafe profile [10]. For verification purposes, we need a formal model of the underlying communication medium which includes the possibility of the communication faults to be considered. We use a grey channel of limited buffering capacity which can delete, modify, and duplicate messages, and produce spurious messages. However, if a message is modified or a spurious message is produced, we assume the CRC2 checksum of the delivered message to be incorrect. This reflects the assumption that corrupted messages occur randomly, and are not introduced maliciously. Since PROFIsafe is only required to protect a system from technical faults, this is a reasonable assumption. Page 142 In any verification task, it is essential to identify and formalise such additional assumptions. Without the above assumption, it would be impossible to prove any useful property of the PROFIsafe protocol. Most verification tasks of industrial applications require similar kinds of abstraction and additional modelling. Unfortunately, carrying out this abstraction is a diffucult task which cannot be performed automatically. The authors believe that this is one of the major obstacles preventing formal verification from becoming commonly used in industry. 4 From UML Statecharts to Finite-State MachinesWe use the model checker of the VALID Toolset to verify the PROFIsafe protocol. The VALID Toolset, developed at Siemens Corporate Technology, supports the modelling, verification and code generation of finite-state machines as deqscribed in [1, 2, 11, 13]. Accordingly, the formalised and abstracted statecharts specifying the PROFIsafe protocol are translated into appropriate finite-state machines. The framework used by the VALID Toolset is that of discrete-event systems (DES) [11, 13]. In this context, a finite-state machine is defined to be a 5-tuple
where Such finite-state machines can be represented graphically as a state
transition graph (e.g. in Figure 3). States are represented
as nodes, with the initial state highlighted by a thick border, and marked
states coloured grey. The transition function Multiple finite-state machines can be composed by synchronisation on
common events. All synchronised state machines repeatedly agree on an event
to be executed next, and simultaneously perform the corresponding state
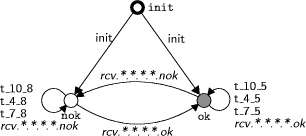
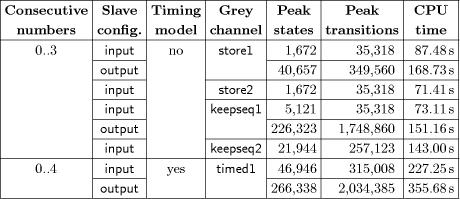
transition. A state transition using an event For more details on synchronous composition and other concepts from the theory of discrete-event systems, please refer to [2, 11, 13]. The framework of finite-state machines used here can be considered as a very restricted subset of UML statecharts. There are no variables, guards, or assignments; only simple events can be used for synchronisation. Page 143 Figure 3: Finite-state machine derived from PROFIsafe F-host statechart. In order to obtain a set of finite-state machines from the UML statecharts constituting the PROFIsafe specification, we perform a two-step translation. In the first step, we create one finite-state machine from each statechart, by deleting all guards and actions from the transitions and replacing them by event labels. For example, the statechart in Figure 2 is replaced by a finite-state machine as shown in Figure 3. This step apparently removes all data dependencies from the transitions. The synchronisation constraints described by the guards and actions on the transitions are introduced into the model by adding one state machine for each variable used in the statechart. As an example, consider the variable representing the CRC2 checksum of the last message received by the F-host. After data abstraction, this variable is modelled as a flag, called in_CRC, which is set if the last message had a correct CRC2 checksum. This variable is represented by a finite-state machine with three states as shown in Figure 4. There are two states ok and nok representing the situation that the flag in_CRC is on or off, plus an additional state init representing a flag with initially undefined value. The flag in_CRC can change its value when a message with correct or incorrect CRC2 checksum is received (events rcv.*.*.*.*.ok resp. rcv.*.*.*.*.nok). Page 144 Figure 4: Finite-state machine for in_CRC variable of PROFIsafe F-host. In addition, the current value of the flag restricts the possible transitions of the main statechart. Consider the transition from state 4 to state 5 of the F-host statechart (Figure 2). This transition can only be taken if the last message received had no faults, i.e. if in_CRC is set. Accordingly, the transition event t_4_5 in the finite-state machine of Figure 3 must be disabled if in_CRC is not set. This constraint is enforced by adding a selfloop labelled with this event to state ok in Figure 4. By constructing such finite-state machines for the statecharts of the F-host and the F-slave and their variables, we obtain a behavioural model of the PROFI- safe protocol. Given that the original UML statecharts are specified using formal notation, the translation into finite-state machines can be performed automatically. This translation process so far has only been carried out for the PROFIsafe model, but based on the experience obtained, it can easily be extended to handle arbitrary statecharts. In addition, we need to model the behaviour of the grey channel. Since no UML description of the grey channel is available, the grey channel has been modelled directly as finite-state machines. different models have been created, representing different fault possibilities and buffering capacities. For the F-host, F-slave, and grey channel together, we obtain models consisting of 300 to 383 finite-state machines, depending on the grey channel and protocol considered. 5 VerificationBased on the finite-state machine model of the PROFIsafe protocol, two steps of verification have been carried out. Firstly, we have performed some standard checks of universal properties in order to find out whether the logic specified by the statecharts is consistent, or whether it contains any undesirable loops or deadlocks. Page 145 Secondly, we have checked whether the protocol satisfies certain application-specific properties regarding failsafe communication. 5.1 Universal PropertiesUniversal properties are defined in a general way for a class of finite-state machines, usually specifying some kind of consistency which developers would like to have satisfied for any system they develop. Their advantage is that they can be checked directly for any system, as a push-button technology, without the user having to provide any additional input. We have checked the PROFIsafe model for the following universal properties. Controllability. A specification is called controllable [11, 13] if it can always cope with any external events which it may receive as input. In the case of a PROFIsafe component (F-host or F-slave), this means that the component must always be able to handle any possible incoming messages as well as any external events such as timeouts. Termination. We have analysed the PROFIsafe specification in order to check whether it permits infinite control-loops [3], i.e. whether it is possible that the execution enters an infinite loop without ever reaching an activity state. This is an important question, since such a control-loop would permit the state machine to get stuck in an infinite execution without ever considering new input events. Confluence. Next, we have checked that the behaviour defined by the PROFI- safe statecharts is confluent [3]. This means that the protocol defines a deterministic behaviour, i.e. that there are no situations in which the specification permits multiple responses, e.g. the sending of different messages, after the same sequence of inputs. Although not essential, such determinism usually is desired by developers. Furthermore, creating test-cases as discussed in Section 6 is much easier based on a con uent model, since there is only one possible response at each state. Nonconflicting. Finally, we have checked whether the PROFIsafe specification is nonconflicting [11, 13]. A model is considered to be nonconflicting if, in every situation, it is always possible to reach a given terminal state. This is a crucial property for any useful specification: if it is not satisfied, this means that the system may run into a livelock or into a deadlock. In our analysis of the PROFIsafe specifications, we have included terminal states by difining a situation of normal operation, which should be reachable from any other state: a communication partner is in a terminal state if it is waiting for new messages during normal operation, all message buffers contain good messages, and no errors are present. Page 146 In contrast to the properties discussed above, the nonconflicting property may cease to hold if the behaviour of the environment is restricted. Non-coflicting only means that the specification can reach a terminal state in cooperation with the environment. If the environment is not cooperative, for example if it does never send a certain message required to reach the terminal state, then a deadlock situation may occur although the specification has been proven to be nonblocking. Therefore, we have performed the non-conflicting check based on different assumptions about the messages which can be received from the grey channel. The PROFIsafe model has been successfully verified to satisfy each of the universal properties listed above. 5.2 Application-Specific PropertiesAs a second step of verification, we have defined and checked several application-specific properties of the PROFIsafe protocol. Most importantly, we have examined whether the requirements of failsafe communication are guaranteed. We have checked whether the occurrence of a fault causes both communication partners to switch to their failsafe states within the required delay time. There are different classes of faults to be considered, such as the occurrence of a corrupted message (CRC fault) or the loss of a message (timeout). For each kind of fault, it is required that, after recognition of the fault, both communication partners switch to their failsafe states. Therefore, for each fault, we have verified separately that the agent recognising the fault and its partner switch to their failsafe states within a certain time limit. As is to be expected, verifying this property for the partner of the agent recognising the fault turns out to be more dificult, since both agents and an appropriate model of the grey channel need to be considered during verification. All the required properties were formally described by additional finite-state machines and verified by VALID using a language inclusion check as described in [1]. This analysis produced a couple of counter-examples, which pointed to some problems in an earlier version of PROFIsafe, and which were used to improve the next version of the profile [10]. 5.3 Experimental ResultsThe table in Figure 5 shows some of the experimental data collected during verification, namely the performance of the nonconflicting checks performed on the PROFIsafe model. Page 147 Figure 5: Experimental data from PROFIsafe nonconflicting checks. As a nonconflicting check always requires the entire model to be taken into account, this is one of the more difficult verification tasks. As explained above and can be seen in the table, the conflict check was carried out on different versions of the PROFIsafe model, considering input and output slave configurations with different ranges of consecutive numbers, and using different grey channel models. The grey channels store1, store2, keepseq1, and keepseq2 are simple grey channels with fixed buffering capacity and the ability to modify messages provided that the CRC2 checksum of the modified message is incorrect. Channels store1 and store2 can also modify a message by just changing its consecutive number and leaving the CRC2 checksum intact; this is used to model a PROFIsafe configuration in which the consecutive number is not included in the CRC2 checksum. Channels store1 and keepseq1 have a buffering capacity of 1, i.e. there can be at most one undelivered message at any time. In contrast, channels store2 and keepseq2 have a buffering capacity of 2. Furthermore, we have created and analysed a PROFIsafe model including timing assumptions, which is needed to verify certain application-specific properties requiring timing constraints. This model has been combined with a grey channel model called timed1 with buffering capacity of 1, the ability to modify messages provided that the CRC2 checksum of the modified message is incorrect, and some assumptions limiting the amount of time how long a message can be kept within the channel. The table in Figure 5 shows some performance data collected when using the VALID Toolset for checking the different PROFIsafe models to be nonconflicting. For each run, the table shows the maximum number of states and transitions constructed by the algorithm: this gives a rough estimate of the amount of memory required. Furthermore, the amount of CPU time consumed for each verification run is given. Page 148 All runs were carried out on a 600 MHz Pentium III processor with 512 MB of RAM. In summary, we can say that the verification of the complete protocol can be carried out within some minutes on a standard personnel computer. However, it was not possible to verify the model after further increasing its complexity. Thus, the models described here must be considered as the most complex models that can presently be handled by the tool. 6 Automated TestingBased on the verified model, we have computed test cases which can be used to execute conformance tests, in order to ascertain that a protocol implementation has the same behaviour as the verified model. These test cases will be made available to vendors of PROFIBUS applications, who will then be able to obtain certificates of conformance for their implementations more easily. In order to generate test cases from a model automatically, we must first specify a coverage criterion. A coverage criterion defines a set of states or transitions which must at least be visited when executing the generated test suite. Which coverage criterion is most useful, depends on the specific application. The usual approach when testing an implementation is to try covering all possible portions of the implementation's code. When testing a PROFIsafe component, this corresponds to executing all transitions of the component's statechart. Yet, such an approach relies on the specific implementation suggested by the statecharts given in the PROFIsafe profile, and does not consider alternative implementations, which may use completely different states and transitions. Therefore, we have considered alternative criteria, which rely on the possible exchange of messages defined by the protocol instead of its statechart representation. For generating our test cases, we have required that, during the execution of the test suite, the component under test should at least once send and receive all possible sequences of two messages, which may occur according to the protocol specification. In this way, we expect to cover the relevant behaviour, since the PROFIsafe standard defines whether a message is to be considered as correct based on the previous message received. Therefore it is sufficient to consider sequences of two messages. Like verification, test case generation is performed on a simplified PROFI- safe model with a limited range of consecutive numbers (0..4 instead of 0..255). Using the full range of consecutive numbers would require more than 10 6 pairs of messages to be considered in each test suite. Such a test suite, besides being impractically large, would include many instances of the same logical behaviour, only with different consecutive numbers. By using the restricted range of consecutive numbers, we obtain test cases which still cover all the relevant logical behaviour and are much better usable. Page 149 In order to actually run the tests, the consecutive numbers from the computed test cases are mapped to the full range in an appropriate way. behaviour and are much better usable.The task of test case generation has been carried out for the PROFIsafe F-slave model. Two test suites have been computed, for an F-slave in input and output slave , respectively. Each test suite contains six test cases, with the largest test case cqonsisting of 2253 events. These test cases are currently used to implement a certified testing environment for F-slave implementations. In a second step, it is planned to do the same for the PROFIsafe F-host. 7 ConclusionsWe have discussed the verification and test case generation for the industrial field bus protocol PROFIsafe. The protocol is specified using a restricted version of UML statecharts, which is free from ambiguities. Afqter applying some abstractions, the statecharts are translated into finite-state machines and analysed using the VALID Toolset. In order to perform the formal analysis, the protocol specification given as UML statecharts has to be translated into a formal model consisting of finite state machines. During the project described here, a specialised translation process was used, which has been implemented only for the PROFIsafe model. Yet, the translation process can be fully automated and applied to other statecharts as well. In the future, we would like to extend it to a more general tool, which can also handle the more complex constructs in general UML statecharts. In the PROFIsafe specification, very simple statecharts are used, which, while exploiting only few features of UML statecharts, have the very clear and unambiguous semantics needed for formal analysis. Based on this restricted statecharts language, it is possible to obtain expressive verification results, which have helped the designers to improve their specification. Furthermore, it is possible to generate test suites with guaranteed coverage, which will be used for automated conformance tests of PROFIsafe implementations. Acknowledgements The authors would like to thank Bertil Brandin for his support and helpful comments in preparing this paper. References1. B. A. Brandin, R. Malik, and P. Dietrich. Incremental system verification and synthesis of minimally restrictive behaviours. In American Control Conference, 2000. Page 150 2. C. G. Cassandras and S. Lafortune. Introduction to Discrete Event Systems. Kluwer Academic Publishers, September 1999. 3. P. Dietrich, R. Malik, W. M. Wonham, and B. A. Brandin. Implementation considerations in supervisory control. In B. Caillaud, P. Darondeau, L. Lavagno, and X. Xie, editors, Synthesis and Control of Discrete Event Systems, pages 185 201. Kluwer Academic Publishers, 2002. 4. EN 50170. European standard for Pro bus-DP and FMS. 5. G. J. Holzmann. The SPIN model checker. IEEE Transactions on Software Engineering, 23:279 295, 1997. 6. Alexander Knapp and Stephan Merz. Model checking and code generation for UML state machines and collaborations. In Proceedings of the 5th Workshop on Tools for System Design and verification, FM-TOOLS 2002, pages 59 64, 2002. 7. D. Latella, I. Majzik, and M. Massink. Automatic verification of a behavioural subset of UML statechart diagrams using the SPIN model checker. Formal Aspects of Computing, 11(6):637 664, 1999. 8. R. Mühlfeld and R. Malik. Anwenderbericht: Veri kation von UML-Statecharts am Beispiel des PROFIsafe-Pro ls. In Rational-Anwenderkonferenz (RAK 2002), 2002. 9. Object Management Group. Unified modelling language specification, version 1.3, 2001. Available at http://www.omg.org. 10. Profibus Nutzerorganisation e. V. PROFIsafe-profile for safety technology, version 1.12, 2002. 11. Peter J. G. Ramadge and W. Murray Wonham. The control of discrete event systems. Proceedings of the IEEE, 77(1):81 98, January 1989. 12. Timm Schäfer, Alexander Knapp, and Stephan Merz. Model checking UML state machines and collaborations. Electronic Notes in Theoretical Computer Science, 55(3):1 13, 2001. 13. W. M. Wonham. Notes on control of discrete event systems, 1999. Systems Con- trol Group, Department of Electrical Engineering, University of Toronto, Ontario, Canada; at http://www.control.utoronto.ca/ under "Research". Page 151 |
|||||||||||||||||
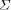 is an alphabet
of events, Q is the state set (assumed finite and
non-empty),
is an alphabet
of events, Q is the state set (assumed finite and
non-empty),  : Q
×
: Q
×  Q is the initial state, and Qm
Q is the initial state, and Qm 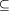 Q is the set of marked or terminal states. The transition
function
Q is the set of marked or terminal states. The transition
function 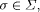 ,
i.e.
,
i.e.  from
a state q1 to state q2 whenever
from
a state q1 to state q2 whenever 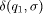 = q2.
= q2.