| Submission Procedure |
An Architecture for a Three-Tier PathFinderMichael Barley Hans W. Guesgen Gareth Karl Abstract: This paper describes the architecture of a route finding system that computes an optimal route between two given locations efficiently and that considers user preferences when doing so. The basis of the system is an A* algorithm that applies heuristics such as the air distance heuristic or the Manhattan heuristic to compute the shortest path between the two locations. Since A* is not tractable in general, island search is used to divide the problem into smaller problems, which can be solved more easily. In addition to that, search control rules are introduced to express user preferences about the routes to be considered during the search. Key Words: route finding, A* search, island search, search control rules Category: I.2.8 1 Route Finding and SearchIn most cities around the world, the number of cars on the roads is still increasing, and therefore it becomes more and more important to implement support for finding a good route from some point A in a city to some other point B. Printed maps are still a valuable aid to determine such a route, but they have severe deficiencies: they only capture the static aspects of the road network, but do not capture dynamic aspects like rush hours or blockages due to accidents. Electronic route finding systems can be more flexible in this respect, and therefore they are likely to replace maps in the near future. As described in [Guesgen and Mitra, 1999] , the two main subsystems of any route finding system are the route planning and route guidance subsystems. Whereas the route guidance subsystem takes a given path through the road network and provides the driver with a description or set of directions to accomplish the task of navigating, the route planning subsystem finds a path through the road network which conforms to the users preferences about the required route. Although both subsystems are equally important, we focus in this paper on the route planning subsystem of a route finding system (called the pathfinder, for short). Page 739 In the ideal case, the path-finder combines a basic search through the road network with knowledge about which roads to prefer or which ones to avoid at certain times. In particular, it should fulfill the following requirements: Optimality. If there is an optimal solution to the problem of finding a route from A to B, the system should be able to compute such a solution. Tractability. In larger search spaces (which are typical for most cities around the world), the system should still be able to compute an optimal solution efficiently. Customizability. The user should be able to add preferences to the system easily and dynamically, which include or exclude certain (types of) roads in the solution. Most research work has focussed on the first two requirements [Pearson, 1998] , using approaches like heuristic search, island search, or hierarchical search. There is little work that addresses the problem of incorporating additional knowledge such as preferences into the search. In this paper, we will focus on the third requirement, showing a way to express preferences and discussing problems that this may cause. Our view of an architecture for an adequate pathfinder includes the following components:
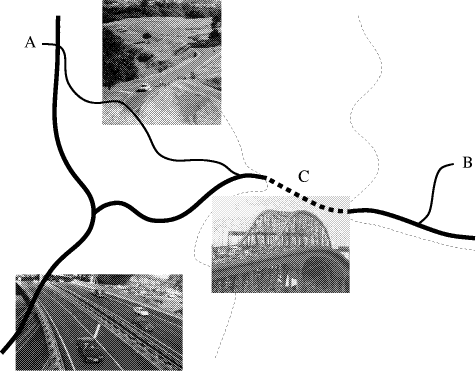
Consider, for example, the situation illustrated in Figure 1, which shows a sketch of the area around the main harbor bridge in Auckland. To get from a point A in central Auckland to a point B on the North Shore, you have to cross the harbor using the bridge indicated by C. An A* algorithm applied to the problem of finding the best route from A to B explores the search space and finally results in a path that uses some ordinary roads to get to the harbor bridge, then enters the freeway to get across the harbor, and finally exits the freeway and uses some ordinary road again to get to point B. Page 740 Figure 1: Schematic route map of the Auckland harbor bridge area. The thick lines indicate freeways and the medium thick ones ordinary roads. The thin dashed lines are shore lines, separating central Auckland from the North Shore. The search can be focussed by introducing C as an island. Instead of searching for the shortest from A to B directly, the search is decomposed into two subsearches: one from A to C and the other from C to B. Generally, two smaller searches are more efficient than one larger search, because of the combinatorial explosion in the search tree. Although the A* algorithm computes the shortest path, assuming that the heuristic is admissible, the resulting route might not be satisfactory from a different point of view. For example, traveling along ordinary roads might be less attractive than taking the freeway, even if this results in a slightly longer route. Page 741 Such a preference can be captured in a search control rule, which can be added to the system by the user. In the rest of this paper, we discuss the three components of the proposed path-finder, focusing on the component that comprises the search control rules. Our emphasis is on the robustness of the search control rules: If new rules are added to the system through interaction with the user, can we guarantee that the system doesn't produce counterintuitive results. More precisely, given a set of control rules which produce intuitive results and given a new rule that on its own produces intuitive results, does the original set of rules and the new rule together produce intuitive results? 2 Optimality: Heuristic Search for Finding the Shortest PathMost heuristic search algorithms used for finding the shortest path
from a point A in a city to a point B are based on the A* algorithm [Hart
et al., 1968]. This algorithm attempts to find an optimal path
from A to B in a network of nodes by choosing the next node x in a search
that minimizes a given cost function f(x) = g *(x)
+ h(x). The cost function adds to the costs from A to x,
given by g *(x), the estimated cost from x to B, given
by h(x). If h(x) never overestimates the real
costs from x to B, the heuristic is admissible (i.e., it is guaranteed
to find an optimal solution). The special case of h A number of heuristics are suggested in the literature which are applicable to the route finding. These heuristic evaluation functions include those that are based on a distance measure dist(x, B), in particular the air distance heuristic and the Manhattan heuristic [Pearl, 1984]. The air distance heuristic is an admissible heuristic while the Manhattan heuristic is inadmissible, as the latter has the potential to overestimate the actual shortest distance. To test the pruning power of the heuristics on a real road network, we performed some experiments in the road network of Auckland, using heuristic search as well as uniform-cost search to find a path from a point A to a point B in the city [Pearson and Guesgen, 1998]. We found that uniform-cost search expands almost every node in the circular area that has A in the center and the distance between A and B as radius. With the air distance heuristic, the search is more focussed and the node expansions describe a more elliptical path. The Manhattan heuristic is even more focussed than the air distance heuristic with a decrease in the size of the minor axis of the ellipse over the air distance estimate. Despite the promising capabilities of the A* search algorithm to prune the search space, search solely guided by heuristics like the air distance or Manhattan heuristics might be inefficient. In a real-time decentralized route finding system (e.g., like the ones used in cars), the user expects to receive an answer almost instantaneously. Systems that are purely based on an A* search are intractable. The next section discusses a way of making the search tractable. Page 742 3 Tractability: Using Island Search to Improve Heuristic SearchA drawback of standard heuristic search techniques is that they do not use any sources of knowledge other than an evaluation function to guide a search from a start to a goal state. If we know, for example, that the best route from A to B has to pass through point C, we can use this knowledge to establish an intermediate state in the search. Rather than search for the shortest path from A to B directly, we split the search into two smaller searches and look for the shortest path from A to C and from C to B, respectively. This idea is utilized in the island search algorithm [Dillenburg and Nelson, 1995]. We can use an arbitrary number of islands for our search. If at least one of the islands lies on the optimal path to the goal state, then directing a heuristic search through this island to the goal has the potential of dividing the exponent in the complexity term. Often, however, there is more than one island that may occur on the optimal path. Island sets that contain more than one island on the optimal path are called multiple level island sets. In the domain of route finding systems, islands correspond to road intersections that are most commonly used when planning a route, such as intersections and bridges. [Chakrabarti et al.,1986] were the first to implement
an algorithm that combined heuristic search with sub-goal knowledge. Their
algorithm, Algorithm I, guides the search through a single island out of
a larger island set IS, finding the shortest path from A to B through
the most favorable node in IS. If the path from A to the current
node x does not yet contain an island, a new heuristic is used,
h(x) = Although Algorithm In never expands more nodes in its search than Algorithm I (provided the optimal path contains E islands) [Dillenburg and Nelson, 1995] , which in turn never expands more nodes than A* [Chakrabarti et al., 1986], it suffers from "island interference". This occurs when the heuristic used by Algorithm In guides the search towards the islands in the wrong order because the node which minimizes dist(x, i) + dist(i, B) (i.e., the island most directly between the current node and the goal node) is not the next island on the optimal solution. Page 743 In this situation, guiding the search towards the correct island could
expand many less nodes. Dillenburg and Nelson do this by altering the heuristic
in Algorithm In to create Algorithm Inp.
This heuristic tries all ordered permutations of the island set with length
E and guides the search towards the first island in the permutation
that resulted in the lowest heuristic value. While this decreases the number
of nodes, it does not necessarily increase the efficiency of the algorithm.
Let IS represent the island set, then the number of permutations
that must be checked for each node expansion is of the order O Although Algorithm I and Algorithm I n have the potential to make route
finding more tractable, they are reliant on the input of an island set
that contains at least one node on the optimal path (E nodes in
the case of Algorithm In ). The selection of islands
for the algorithms is not an obvious process. The time taken to select
the islands must be so small that it does not offset the gain of the island
search over A*; correct islands must be selected all or almost all the
time; and the island set must be small enough so that the island search
is fast. If an island selection algorithm turns out to be too slow, then
preconditioning can be used: the island sets can be precalculated and stored
with the graph data. If the algorithms are likely to return all incorrect
islands for some searches, then an Possible approaches to selecting islands include selecting the nodes with the most neighbors; selecting the busiest intersections; modeling obstacles in the road network; and creating rules for individual islands that specify whether that island should be in the island set. Large intersections, i.e. nodes with many edges, are more likely to be on faster roads and therefore optimal routes between nodes. Clearly only nodes that are near or between the start and goal nodes are good prospects for islands. Page 744 For this reason we wrote an algorithm that creates a subgraph of the road graph containing only those nodes in a rectangle that has the start and goal nodes at opposite corners and then finds the nodes in the subgraph with the most edges. This algorithm is linear with respect to the number of nodes in the graph and proved to be effective at selecting islands. Over testing done on the Auckland road map, it returned island sets with an average of 20% correct islands. Also, the number of islands returned can be easily specified as required. [Dillenburg and Nelson, 1995] suggest selecting islands based on the most used intersections in the network. Both Dillenburg and Nelson; and [Pearson, 1998] tested this. Pearson broke Auckland up into 4km2 regions, calculated all shortest paths between a pair of regions and chose the top 5% of most common nodes in these paths as islands. He observed that for many pairs of regions the most common nodes occurred on only 65% of routes, but as long as E members of the island set occur on the route, then the algorithm finds an optimal solution. Since all the shortest paths between the regions must be calculated, this island selection algorithm is very slow and the island sets must be stored. However, breaking Auckland up into 4km2 regions would result in around 600 regions. Since an island set would be required for each combination of two regions, around 360,000 island sets would have to be stored. Therefore larger regions than this may be required. As the regions become larger, the amount to be stored reduces but the accuracy of the island sets decreases, it would be important to find a compromise. [Dubois and Semet, 1995] suggest modeling obstacles in the road network. These obstacles are then represented by line segments. For example, a long thin obstacle may be represented by a single line segment while a concave shape may need up to three. They used the ends of these line segments not as islands in a form of island search (indeed, these ends may not even be nodes in the graph) but only in a heuristic for calculating a lower bound on the distance between these nodes. This new heuristic, while still being admissible, has a value always more than or equal to the air distance heuristic and so is a better heuristic to use in an A* search. This idea could be altered so as to create line segments that stretch from one node to another. When a line from the start to the goal node intersects one or more of these line segments, the ends of the segments would be included in the island set. Alternatively, nodes with strong potential as islands could be chosen and rules written to specify when and when not to add them to the island set. These rules would be based on the longitude and latitude of the start and goal nodes. For example, if one of the nodes has coordinates that indicate it is on the North Shore while the other is in central Auckland, then the harbor bridge node would be added to the list. Page 745 For shorter search distances the gains made by island searches over A* are minimal, and with some selection algorithms the difficulty of selecting correct islands increases. It therefore makes sense to calculate the air distance between the start and goal nodes and only use island search if the distance is above a certain threshold. 4 Customizability: Search Control RulesWe know that A* can come up with optimal routes given an admissible heuristic. We have talked about decreasing the cost of finding an acceptable path by using islands to decompose the global path problem into a sequence of local path problems. However, we have not addressed the problem of constraining the solution to satisfy user-defined constraints and capabilities. Different users have different constraints and different capabilities. While we want to design a general path-finder, we want to be able to easily tailor it to fit individual users. One user might want to constrain the path-finder to use freeways over using side streets whenever freeways are available and won't impose too much extra cost, while another user might want to avoid traffic circles at all times, etc. In short, constraints say when to eliminate certain alternatives (edges) from the search space. In addition to having different preferences, users also can have different capabilities. For example, a driver of a 4-wheel Jeep might consider driving across unpaved roads, across "fordable" streams, etc., that drivers of most other vehicles would not consider suitable. Since most users would not consider these possibilities as being appropriate, they would be excluded from the path-finder's default search space. If the user want to extend the default search space, they would need to describe how to extend the space (i.e., what edge to add) and under what conditions. For example, a person owning an amphibian vehicle might want the path-finder to consider routes that included water paths from publicly accessible beach to publicly accessible beach whenever the beaches are less than 2 miles apart. We are defining capabilities to be these descriptions of how and when to extend the search space. Prodigy [Minton, 1988] is perhaps the best known system that affords the user the capability or adding and/or removing edges from the default search space. Prodigy does this via search control rules. Prodigy search control rules have preconditions and postconditions. The preconditions test the state of the current partial solution candidate and/or the state of the problem-solver. The postconditions describe an edge and whether they are adding or removing it. Rules that add edges are called generation rules and rules that remove edges are called rejection rules. Our path-finder would generate its search space in phases. Given a node in the search tree, a default set of children would be generated, generation rules are then run to possibly add candidate edges to the set, then the rejection rules are run to possibly remove edges from that set. Page 746 The candidate set is passed from phase to phase, being updated by each phase. Those candidates remaining in the set at the end would be added into the open set of nodes for A* to select from. Example encodings of the amphibian car's generation rule and the "avoid side roads when freeway is affordable" rejection rule are: IF: (AND (CURRENT-LOCATION
<B1>) IF: (AND (CURRENT-LOCATION
<L>) THEN: (REJECT-PATH <P1>) These types of search control rules seem a reasonable approach to allowing the user to incrementally modify the space searched by A* as their preferences and capabilities change. However, are there hidden dangers in using these types of search control rules? In particular, we would like the user to be able to look at the rule and have an intuitive idea of its effect upon the search space. For example, if the user adds a generation rule to the search control rule set, then intuitively they would expect the search space to be a superset of what it was before the rule was added. Since one of the often touted advantages of rule-based systems is the relative additivity/independence of rules [Barr and Feigenbaum, 1981, page 193], we would expect this to be the case. If users cannot predict the effects of a rule in isolation, then they must try to understand the interactions between the proposed new rule and the current set of rules. This is an unrealistic demand on most users. Unfortunately, it turns out that for these types of search control rules, the effects of adding a rule cannot be predicted from looking at it in isolation from the current set of rules. In fact, the effects of modifying the rule set in any way can be counterintuitive. For example, adding a generation rule can cause the search space1 to be smaller, etc. We illustrate this with the following example. Assume that the default generation of path candidates includes all roads that our local database describes as intersecting our current location and as not being under construction. Also assume that our current set of search control rules consists solely of the "avoid side roads when freeway is affordable" rejection rule shown previously.
1Where we only focus on the topology of the space, not its traversal. Page 747 Finally, assume that in our local database the only freeway that intersects our current location is a proposed freeway that is still under construction. Given this situation, the default generation phase will not propose any free-way candidates since the proposed freeway is still under construction and no other freeway intersects our current location. There are no generation rules; no additional candidates will be added to the default set. Thus the set of candidates passed to the rejection phase will not have any freeway candidates and the "avoid side road . . . " rejection rule will not be triggered, leaving the path-finder to use side roads to get closer to the destination location. Now, consider the following generation search control rule: IF: (AND (CURRENTLOCATION
<L>) This rule proposes any freeway as a candidate that intersects the current location. This is an overly general rule, it will propose candidates that turn out not to be useful (e.g., because they are under construction, etc.). However, because it is a generation rule, one's intuition from looking at the rule in isolation is that its affect upon the search space is to possibly add edges, i.e., that the edges in the new search space will be a superset of the edges in the original search space). Unfortunately, examination of the current rule set and analyzing the interactions between this new generation rule and the "avoid side road . . . " rejection rule show that the side road edges will be removed from the search space. In other words, adding a new generation rule can indeed cause the search space to contain fewer edges. In this particular case, the addition of this new generation rule has eliminated all solutions to this route-finding problem from the search space. This is clearly unacceptable behavior from the user's viewpoint. They added a rule which appeared to be simply adding edges to the search space, but, which because of interactions with existing rules, also removed edges and consequently prevents the path-finder from being able to solve navigation problem which were previously solvable. Does this mean that search control rules are an inappropriate mechanism for allowing a user to describe their constraints and capabilities? Not necessarily, it depends upon what aspects of the search control rules allow the effects of adding new rules to be counterintuitive and upon what alternatives we have for handling those aspects. What is it about this search control rule language and/or search control architecture that enable these counterintuitive changes to occur? In our example, it is the test for the presence of freeway candidates that led to the rejection of the side roads. Page 748 This type of counterintuitive behavior would be eliminated if the preconditions of search control rules were limited to testing for the candidate appearing in the rule's postcondition and to testing for commitments already made in the current partial solution to the user's route-finding problem. This approach to avoid allowing counterintuitive behavior to arise from the modification of the search control set may solve the problem, but does so at the cost of prohibiting the rules from examining which alternatives are available at a choice point. Unfortunately, such examinations are often desirable, e.g., in our example rejection rule we only want to reject the side roads if a freeway is an acceptable alternative. So, it is not obvious that such restrictions would be the best way to avoid these counterintuitive behaviors. This is something that needs more research. 5 SummaryIn this paper, we introduced an architecture for an optimal, tractable, and customizable route finding system. The main components of the system are based on the following:
The three components use different types of knowledge. Search control rules establish the search space and determine the potential successors of the nodes. Island search divides the resulting search into subspaces. Heuristic search traverses the search subspaces. We have implemented the first two components of the path-qfinder and tested them with the Auckland road map. Implementation on the third component is yet to be done, and it remains to be seen whether the problem of adding search control rules incrementally and obtaining counterintuitive results does occur frequently and therefore has be catered for. References[Barr and Feigenbaum, 1981] A. Barr and E.A. Feigenbaum, editors. The Handbook of Artificial Intelligence, volume 1. William Kaufmann, Los Altos, California, 1981. [Chakrabarti et al., 1986] P.P. Chakrabarti, S. Acharaya, and S.C. de Sarkar. Heuristic search through islands. Artificial Intelligence, 29:339-348, 1986. [Dillenburg and Nelson, 1995] J.F. Dillenburg and P.C. Nelson. Improving search efficiency using possible subgoals. Mathematical and Computer Modelling, 22(4-7):397-414, 1995. Page 749 [Dubois and Semet, 1995] N. Dubois and F. Semet. Estimation and determination of shortest path length in a road network with obstacles. European Journal of Operational Research, 83:105-116, 1995. [Guesgen and Mitra, 1999] H.W. Guesgen and D. Mitra. A multiple-platform decentralized route finding system. In Proc. IEA/AIE-99, pages 707-713, Cairo, Egypt, 1999. [Hart et al., 1968] P.E. Hart, N.J. Nilsson, and B. Raphael. A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 4(2):100-107, 1968. [Korf, 1996] R.E. Korf. Artificial intelligence search algorithms. Technical Report TR 96-29, Computer Science Department, UCLA, Los Angeles, California, 1996. [Minton, 1988] S. Minton. Learning Search Control Knowledge. Kluwer, Dordrecht, The Netherlands, 1988. [Pearl, 1984] J. Pearl. Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley, Reading, Massachusetts, 1984. [Pearson and Guesgen, 1998] J. Pearson and H.W. Guesgen. Some experimental results of applying heuristic search to route finding. In Proc. FLAIRS0-98, pages 394-398, Sanibel Island, Florida, 1998. [Pearson, 1998] J. Pearson. Heuristic search in route finding. Master's thesis, Computer Science Department, University of Auckland, Auckland, New Zealand, 1998. Page 750 |
|||||||||||||||||
 0 is often referred to as uniform-cost search [Korf, 1996].
0 is often referred to as uniform-cost search [Korf, 1996]. 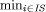 {dist(x, i) + dist(i, B)}. However if the path to x
does already contain an island, the original heuristic h(x)
= dist(x, B) is used. [
{dist(x, i) + dist(i, B)}. However if the path to x
does already contain an island, the original heuristic h(x)
= dist(x, B) is used. [ , whereas with Algorithm In it is
clearly only O(|IS |). Therefore, Algorithm Inp
becomes unusable when the size of the island set is large or E is
large. This problem can be avoided if an a-priori ordering of islands is
known. We implemented an algorithm that works on the assumption that the
islands in the island set have an ordering. Unlike the original algorithm,
the new algorithm can restrict itself to finding a choice of E islands
in the given ordering with the lowest heuristic value. The number of permutations
checked by this algorithm's heuristic is of the more reasonable order O
, whereas with Algorithm In it is
clearly only O(|IS |). Therefore, Algorithm Inp
becomes unusable when the size of the island set is large or E is
large. This problem can be avoided if an a-priori ordering of islands is
known. We implemented an algorithm that works on the assumption that the
islands in the island set have an ordering. Unlike the original algorithm,
the new algorithm can restrict itself to finding a choice of E islands
in the given ordering with the lowest heuristic value. The number of permutations
checked by this algorithm's heuristic is of the more reasonable order O
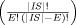 . Details about this algorithm can be found elsewhere
[
. Details about this algorithm can be found elsewhere
[ admissible
version of island search can be used. An
admissible
version of island search can be used. An