Pedagogical Principles for Evaluation of Hypermedia-Based Learning Environments in Mathematics

Abstract: This paper discusses evaluation of hypermedia-based learning environments mainly from the point of view of the learner or student. The evaluation of a learning environment should be based on modern learning theories. These emphasise the importance of constructivism and the learner's activity in building mental models of the mathematical knowledge. The environment should also support conversational and collaborative learning. From the point of view of the learner it should be intentional and provide real life situations and contexts to motivate the study of abstract mathematical contents. Also, it should give sufficient feedback and be able to adapt to the needs of various learners. The purpose of the paper is to discuss basic pedagogical principles that may serve as starting points and guidelines in the evaluation of hypermedia-based learning environments. Two existing hypermedia learning environments will be introduced and evaluated on the basis of the pedagogical principles presented.

Key Words: Hypermedia-based learning environment, evaluation, constructivism, collaboration, intention, context, transfer, reflection.

1 Introduction

Rapid development of information technology, especially in hardware, software, and telecommunication, has increased the potential of technology in education. To take full advantage of the possibilities that modern information technology provides, learning theories must be developed and incorporated into the design of computer based learning. Modern learning theories emphasise the importance of context and collaboration when integrating technologies in learning. Constructivism has risen to be an essential theory in the research of technology-based learning environments. This approach has been applied in the mathematical sciences, too. Constructivism learning is seen as a building process in which learners have an active role and learning is based on their cognitive functioning. The learners obtain new knowledge by constructing it on the basis of their earlier knowledge, upon their active

functioning in continuous interaction with the surrounding reality and other learners. The purpose of this paper is to introduce important pedagogical principles that can be used as guidelines in the evaluation of learning environments. The proposed qualities of learning are based on the list proposed by Jonassen [1995]. The rules of the use of technology in the evaluation on learning environments are based on Jonassen's list of qualities of meaningful learning.

A "moderate" constructivistic approach [Reusser 1991a] emphasises teacher's and content provider's essential role in cognitive development and knowledge construction using carefully designed and presented learning materials, and technologies. Tutoring and teacher's functions support learning as well as appropriately designed didactic materials and they give students possibilities to develop their skills and become more independent and self-regulated learners.

The above principles will be applied to two existing hypermedia learning environments; Solver and Mathematical Microworld for WWW (MMWWW). Solver is a technology based learning environment for mathematical word problem-solving, intended to be used in schools as an additional material. MMWWW contains university level mathematics courses in the form of hypermedia. These courses can be studied on the Internet. The environments will be presented and analysed in respect to the list of qualities of meaningful learning. [Ruokamo-Saari, H., Pohjolainen, S. 1997.]

2 Seven Qualities of Learning

We would like to emphasise the seven qualities of learning, given below, suitable in learning from school to university level. This list of qualities of learning is based on Jonassen. The authors have joined the conversational and collaborative qualities in Jonassen's list into one and added the quality of transfer into the list. From our point of view the seven qualities of learning are as follows:

1. Active - Learners' role in learning process is active; they are engaged in mindful processing of information and they are responsible for the result.
2. Constructive - Learners construct new knowledge on the basis of their previous knowledge.
3. Collaborative - Learners work together in building new knowledge in co-operation with each other and exploiting each other's skills.
4. Intentional - Learners try actively and willingly to achieve a cognitive objective.
5. Contextual - Learning tasks are situated in a meaningful real world tasks or they are introduced through case-based or problem-based real life examples.
6. Transfer - Learners are able to transfer learning from the situations and contexts, where learning has taken place and use their

Page 293

knowledge in other situations.

7. Reflective - Learners articulate what they have learned and reflect on the processes and decisions entailed by the process.

All these qualities are interactive, interrelated, and interdependent with each other. In what follows the authors will use these qualities of learning when evaluating the two mathematical learning environments.

3 The Use of Technology in Learning

Jonassen [1995] presents some assumptions about technology in learning. In his point of view educational technology can be seen as follows:

• Technology is more than hardware. Cognitive learning strategies, critical thinking skills and replicable, applicable techniques can be engaged with the learner via using technology.
• Learning technology can engage learners in knowledge construction and meaning-making.
• Knowledge construction is not supported by technologies used as conveyors of instruction that prescribe and control all learners interaction.
• Technologies will support knowledge construction better when they are need- or task-driven, when interactions are learner-initiated and learner-controlled, and when interactions with the technologies are both conceptually and intellectually engaging.
• Technologies as tool kits enable learners to build more meaningful personal interpretations and representations of the world. They must support the requisite intellectual functionality of the learning requirements of the course of the study.
• Learners and technologies should be intellectual partners. Cognitive responsibilities for performing should be distributed by that part of the partnership that performs it best.

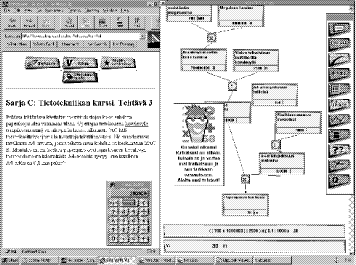
The useful principles listed above should be used in pedagogic design and evaluation. According to Reusser [1995] the design of a computer-based instructional system should be based on content specific research of learning and comprehension and pedagogical model of the learner and the learning process. In designing computer-based teaching and learning environments, real didactic tasks should be considered. One should think thoroughly what to teach and how to teach. The essence of pedagogical design is in the didactic analysis of concepts, structures, representations, learning methods, skills, and strategies and learning models in relation to task or domain specific factors.

These guidelines about technology in learning should also be used in the evaluation

of hypermedia-based learning environments. In the next section two existing hypermedia based learning environments will be evaluated in respect to the principles given above.

4 Evaluation of Two Hypermedia-based Learning Environments

4.1 Case Solver - a Learning Environment for Solving Mathematical Word-Problems

Solver is a technology-based learning environment that also includes different presentation forms of hypermedia (e.g. hypertext, graphics, animation, sound, video) and network properties, social interaction, physical learning activities and mental thinking processes in learning situation [See Ruokamo-Saari 1996a; b.].

Solver has been used to study the connection between the level of students' mathematical giftedness and development of their problem-solving skills when working in a technology-based learning environment [Ruokamo-Saari 1997a; b]. Solver was designed on the basis of an existing computer-based program developed for word problem-solving by Reusser et.al. HERON [see Reusser 1988, 1991a, 1991b; Staub et.al. 1994; Reusser 1995]. In the Solver environment students solve word problems by constructing solution trees with cognitive tools. This process ends up with final result that solves the problem posed in the text.

In Solver the properties of on- and off-line hypermedia are connected together. The on-line part was designed to be used via the WWW and the off-line, local part was programmed with Multimedia ToolBook 3.0. Figure 1 presents the design of Solver application (in Finnish): the tools, solution tree, and equation in off-line ToolBook application are on the right and the tools and problem text of an on-line HTML document are on the left.

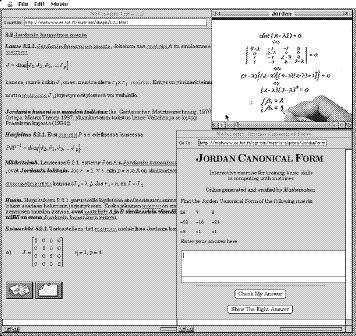
Problem tasks, hints, the model solutions, and a bulletin board are programmed using HTML, so that these can easily be distributed via network, and they can be updated later on. In creating the problem situations a contextual approach was adapted: the topics chosen for the word problems was based on student inquiry: the students were asked about real life problems they would like to solve. Video material was produced to introduce the problem situations for students.

In the problem text there are hot words. By activating them students can get definitions, rules, formulas, and other information about the subject. If a problem is too complex to solve, the user may select the hint tool to obtain tips for constructing the solution. Students may ask hints from each other in problematic situations when constructing the solutions. Using the bulletin board, students are able discuss with other students or with their teacher methods for solving the problems. On the basis of these conversations they can further develop their own constructions.

In the program the model solution for a given mathematical problem is presented step by step, and the students are assumed to discover the solution procedure. Gifted students can probably find shorter or alternative ways to solve the problems. The students' solutions can also be saved and analysed later on.

Some Principles of Tutoring

Solver does not tutor students in the problem-solving process, unless asked for help or hints. This property was thought to be suitable for especially gifted problem-solvers who do not necessarily need any tutoring but are able to conduct autonomous and

original problem-solving. Tutoring was designed with those students' needs in mind who had difficulties in problem-solving. It is also important that students have a chance to notice by themselves possible mistakes they make during problem solving. When a user asks for a hint during the solution-process, Solver tries to find context sensitive hints related to the user's situation in his/her solution. If the user's way of constructing the solution is very original and Solver can not help him/her, it asks the student to try to find support from other students via bulletin board or to go on and check the final result at the end with the checking tool.

The user can start modeling in any situation and move on to an open solution space. In principle, he/she is able to construct the whole solution without tutoring until the final stage, where Solver asks the student to evaluate the final equation. If the user makes mistakes in constructing the solution, the checking tool informs him or her about wrong results. After checking the results, the user can see a representation of the model solution and can compare it with his/her own solution. Even if the solutions are not similar, they can be correct. All the students solutions are saved to files, so that the problem-solving processes can be examined and compared later on. The new solutions proposed by the student can be used as examples of alternative ways to construct solutions.

4.2 Case: Mathematical Microworld on WWW

The pilot hypermedia material consists of two university courses: Introduction to University Level Mathematics and a course on Matrix Algebra. The purpose of the first course is to review school mathematics and to provide help and support for mathematical problems that students will be facing at the university level. The second is a postgraduate course in mathematics at Tampere University of Technology (TUT). The courseware has been designed to be used on the WWW [Antchev et.al. 1996] (http://matwww.ee.tut.fi). The structure of both of the courses consists of text, a mathematical dictionary or database of definitions of mathematical concepts, exercises, examples, and computer aided interactive exercises. The most important mathematical ideas algorithms and problems are clarified with animations and video clips. The mathematical concepts in the lecture notes are linked to the corresponding definitions in the mathematical dictionary or the definition database to provide on-line help for understanding them. Exercises, with hints and examples, are given as a part of the lecture notes. The symbolic algebra package, Mathematica, is used for interactive exercises; it generates various numerical and symbolic exercises, and checks the answers given by students. Interactive exercises provide feedback for the students. In a typical interactive exercise the computer will pose a problem and ask the student to fill in an on-line form. In some cases the user may be asked to answer the problem. The answer will be assessed and a message will be returned describing whether the answer is correct or what went wrong. A part of the problem's data is randomised so that the students can work out several problems of the same type, successively. They may explicitly ask for "new values" to be generated by pressing a

designated button, or students may simply arrive several times at the same node. Additionally, the numerical simulation program Matlab is used as a part of the numerical exercises.

The basic structure of the hypermedia courses is based on the experiences that the authors have got from constructing a stand-alone hypermedia learning environment for Macintosh [Pohjolainen et.al. 1994, 1997]. Positive classroom experiences encouraged us to extend the basic design ideas for the WWW version [Multisilta et.al. 1994, Pohjolainen et.al. 1996]. Communication between distant learners and teachers is supported by bulletin boards, e-mail, and video conferencing software.

Studying Matrix Algebra on the WWW

A general view of the learning interface in the course of Matrix Algebra is given in Figure 2. The instructional material consists of lecture notes divided into chapters and subchapters, a concept definition database, exercises, interactive exercises, animations, and videos. In the figure the student is reading the subchapter on the Jordan Canonical Form. On the left hand side there is a page from the lecture notes (in Finnish). The links starting from the mathematical concepts to their definition files can be seen as the anchor words and they are underlined or of a different colour. The student has also opened a video tutorial that shows how to find the Jordan Canonical Form for a given matrix. At each stage of the solution the video tutorial presents the theoretical results that are needed for the next stage. The hand-writing in the video window is used to tell the student: this is what you should do. Since video clips contain sound, they give a possibility to pass oral information to students. This is useful to teach the pronunciation of Greek letters, names of mathematicians, (foreign) names of methods, and so on. Looking and listening to the video may help the student to solve a related interactive exercise, generated by a symbolic algebra program Mathematica (lower right hand corner) [Antchev et.al. 1995]. From this point of view it is useful that the video can be stopped and be viewed frame by frame. Once the student has found the solution, he or she may write it down in a box provided. After that, the computer checks the solution and informs the student about the result. The correct solution can be seen by pressing the "Show the right answer" button. If the student wants to find the Jordan Canonical Form for another matrix, he/she may ask for a new matrix by pressing the "New Values" button. Care has been taken to keep the problems sufficiently simple. All the matrix algebra interactive exercises can be solved with integer matrices, with small integer elements. Currently there are 15 interactive exercises in the course of matrix algebra.

In addition to Figure 2, the microworld contains exercises, mostly theoretical, with two hint levels. The first hint level explains the problem in more detail and the second hint level informs about the right path for the proof of the solution. All this textual material is given as hypertext, and links to the definition files are available.

As a part of the hypertext lecture notes, a student can find previous examination problems. These can also be read as hypertext with links to the definition files, and they can be used also as test questions for self-study.

At the end of each page there are two buttons which give possibilities for student-teacher interaction. The student can open the bulletin board and communicate with other students and a teacher of the course by pressing the leftmost button at the lower left corner of the lecture notes in Figure 2. The button on the right opens a form for e-mail between the student and the teacher.

Students may also contact the teacher in a more personal way. At the end of each page of the hypernotes they may find buttons to send e-mail to the teacher. This feature will be used to give the students personal assistance, to receive their solutions to given problems, and to give them personal feedback. The possibility of attaching documents with e-mail is especially useful, since it allows the sender to point out details on the WWW material.

In the next section Solver and MMWWW will be evaluated and compared on the basis of the seven qualities of an appropriate learning environment presented earlier.

5 Evaluation of Solver and MMWWW

A direct comparison of the two hypermedia learning environments is rather problematic because of the differences in their design principles, user groups, and goals. Solver is a technology based learning environment for mathematical word problem-solving, intended to be used in schools as additional materials. MMWWW contains university level mathematics courses in the form of hypermedia. The courses can be studied over the Internet. In spite of the differences in the nature of the environments, the authors still feel the comparison to be useful, but rather in the sense that environments are evaluated in regard of the seven qualities rather that compared against each other.

In Table 1, Solver and MMWWW are compared in regard to the seven qualities of appropriate learning environment presented above.

6 Conclusions

In this paper seven important qualities of learning have been introduced and used in the evaluation of hypermedia learning environments for the mathematical sciences. Two learning environments; Solver and MMWWW, have been evaluated on the basis of the qualities presented. Solver was designed for secondary school level for mathematical word problem-solving and MMWWW contains university level courseware on the web. In regard to the seven qualities presented, the learning environments can be improved in many ways.

To strengthen the qualities of activity, constructivity and collaborativity in the Solver environment it might be useful to include a tool to enable students to show their solution trees to other students. On the basis of these solution trees, which are visible for everybody, all the students could elaborate jointly their problem-solving processes. It should also be useful if students were able to point out situations from their solution trees, and to reconstruct them in collaboration with other students. Students should also be able to save their correct solution trees as model solutions, if these differ from the solutions given by Solver. Multiple model solutions can also be used to improve the functioning of the hint tool. Currently the hint tool can give hints only when the students' solution tree resembles the given model solution. This would also improve the context sensitivity of the hint tool.

In the MMWWW learning environment the students activity should be strengthened in construction of knowledge. Students should have special tools to support knowledge construction, e.g. the use of mathematical programs such as Maple and Matlab should be integrated to be an essential part of the learning tasks. This would also strengthen the students' activity, intention and reflection, as they could elaborate and solve "real world" problems using sophisticated theoretical methods.

Secondly, collaboration is not supported strongly enough in MMWWW. The students need more specific exercises and tasks to be solved in collaboration. Currently the students may send e-mail and discuss with other students and teachers via bulletin board, but the use of communication tools is not integrated with the learning tasks. Students' reflectivity should be improved, too. They should be able share and discuss their learning processes with other students, get feedback and guide their learning processes further on. In addition to interactive exercises and hinted exercises, students need more tools to express their real understanding and to evaluate their learning processes and more open tasks should be included in the learning environment to improve the property of reflection.

From the author's point of view the evaluation of learning environments has been

useful, and the results will be used to improve the existing learning environments and they will guide our research and development work further in the field on web-based open learning environments.

References

[Antchev, K., Multisilta, J., Pohjolainen, S. 1995] Antchev, K., Multisilta, J., Pohjolainen, S.: "Mathematica as Part of a Hypermedia Learning Environment"; International Mathematica Symposium, Southampton, July 16-20 (1995).

[Antchev, K., Luhtalahti, M., Multisilta, J., Pohjolainen, S., Suomela, K. 1996] Antchev, K., Luhtalahti, M., Multisilta, J., Pohjolainen, S., Suomela, K.: "A WWW Microworld for Mathematics"; Proc. Ed-Telecom'96, AACE Publishing, Boston, Mass., USA (1996), 5-10.

[Jonassen, D.H. 1995] Jonassen, D.H.: "Supporting Communities of Learners with Technology: A Vision for Integrating Technology with Learning in Schools"; Educational Technology, 35, 4 (1995), 60-63.

[Multisilta, J., Pohjolainen, S. 1994] Multisilta, J., Pohjolainen, S.: "Implementation of Authoring Tools for Hypermedia Based Learning Environments in Mathematics"; Proc. CALISCE 94, Paris, France (1994). Available at http://matwww. ee.tut.fi/Docs/paris/paris.html.

[Pohjolainen, S., Multisilta, J., Antchev, K. 1994; 1997] Pohjolainen, S., Multisilta, J., Antchev, K.: "Hypermedia Learning Environment for Mathematics"; Human Interactions on Symbolic Computation, Workshop, RIACA, Amsterdam March 10-11 (1994), also in S. Pohjolainen, J. Multisilta, K. Antchev.: "A Hypermedia Learning Environment for the Mathematical Sciences"; Chapter in the Book: Human Interaction in Symbolic Computation. Texts and Monographs in Symbolic Computation Springer (1994; 1997).

[Pohjolainen, S., Multisilta, J., Antchev, K. 1996] Pohjolainen, S., Multisilta, J., Antchev, K.: "Matrix Algebra with Hypermedia"; Education and Information Technologies Vol. 1 (1996), 123-141.

[Reusser, K. 1988] Reusser, K.: "Problem Solving beyond the Logic of Things: Contextual Effects on Understanding and Solving Word Problems"; Instructional Science, 17, 14 (1988), 309-338.

[Reusser, K. 1991a] Reusser, K.: "Intelligent Technologies and Pedagogical Theory: Computers as Tools for Thoughtful Teaching and Learning"; Paper presented at the Fourth European Conference for Research on Learning and Instruction EARLI, held at Turku, Finland, August 24-28 (1991).

[Reusser, K. 1991b] Reusser, K.: "Tutoring Systems and Pedagogical Theory: Representational Tools for Understanding Planning and Reflection in Problem-Solving"; Universität Bern, Abteilung Pädagogische Psychologie, Forschungsbericht/Research report No.9 (1991).

[Reusser, K. 1995] Reusser, K.: "From Cognitive Modeling to the Design of Pedagogical Tools"; In S. Vosniadou, E. De Corte, R. Glaser, H. Madl (Eds.). International Perspectives on the Design of Technology-Supported Learning Environments, Hillsdale, NJ: Lawrence Erlbaum (1995), 81-103.

[Ruokamo-Saari, H. 1996a] Ruokamo-Saari, H.: "Hypermedia Learning Environment for Especially Mathematically Gifted Students for Mathematical Word Problem-Solving"; In: P. Carlson, F. Makedon (eds.) Educational Multimedia and Hypermedia, 1996, Proc. Ed-MEDIA 96, AACE Publishing, Boston, Mass., USA (1996), 804.

[Ruokamo-Saari, H. 1996b] Ruokamo-Saari, H.: "Designing Hypermedia Learning Environment for Solving Complex Mathematical Word Problems"; In L. Aho (Ed. ) Learning in Multiple Contexts. Papers and posters presented at the First Joensuu Symposium on Learning and Instruction, Bulletins of the Faculty of Education, University of Joensuu, N:o 62, (1996), 141-158.

[Ruokamo-Saari, H. 1997a] Ruokamo-Saari, H.: "Development of Mathematical Word Problem-Solving Skills in a Technology-Based Learning Environment for Mathematically Gifted Students: A Teaching Experiment"; In T. Väliharju & MLE-group (Eds.) Digital Media as a Learning Environment, University of Tampere Computer Centre Publication Series No. 4, 85-100.

[Ruokamo-Saari, H. 1997b] Ruokamo-Saari, H.: "Mathematical Giftedness and Development of Mathematical Word Problem-Solving Skills in a Technology-Based Learning Environment: a Teaching Experiment"; Proc. Ed-MEDIA'97, AACE Publishing, Calgary, Canada, (1997), 923-927.

[Ruokamo-Saari, H., Pohjolainen, S. 1997] Ruokamo-Saari, H., Pohjolainen, S.: "Pedagogical Issues for the Design of a Hypermedia-based Learning Environment (HBLE)". ), D. Dicheva & I. Stanchev (Eds.), Proc. IFIP WG 3.3 Working Conference, Human Computer Interaction and Educational Tools (HCI-ET, Sozopol, BULGARIA (1997), 82-91.

[Staub, F.C., Stebler, R., Reusser, K., Pauli, C. 1994] Staub, F.C., Stebler, R., Reusser, K., Pauli, C.: "Improving Understanding and Solving of Math Story Problems through Collaborative Use of a Computer Tool (HERON)"; Paper to be presented in a structured poster session on "Children's understanding of mathematical "knowledge" at the Annual Meeting of the American Educational Research 9 Association, New Orleans, April 4-8 (1994).