| Submission Procedure |
|
|
|
|||||||||||||||
Inexact Information Systems and its Application to Approximate Reasoning
Abstract: The inexact information system is based on linguistic terms which have values lying in the interval [0,1]. Imprecision has advantages, because fuzzy sets avoid the rigidity of conventional mathematical reasoning and computer programming. Fuzzy quantifiers are made explicit by means of fuzzy logic. Many systems, for example, complex biological processes, cannot be programmed in a precise way. With fuzzy sets the implicit quantifiers can be easily translated into machine usable form. This paper discusses a method for the description of fuzzy quantifiers in formal languages. A comparison between approximate reasoning and the method of linear interpolation is made. Inexact information in biological and medical expert systems, and the reliability inferences based on it, are also discussed. Key Words: Linguistic approach, fuzzy implication, fuzzy quantifier, fuzzy number, approximate reasoning, information system. 1 Introduction
In convectional information systems there is strong operation consequence following a given algorithm. The direction is from definite digital for any kind of quantitative information to a fixed computer program. For the process of decision making to be successful there must be an exact and full description of the problem to be solved. In an inexact information system linguistic terms are used the values of these linguistic terms are inexact, and there is sometimes only a vague idea of how to interpret them. Humans tend to use words rather than numbers to describe how systems behave. Words are a form of inexact information appropriate to communication, and used in complex biological, economical and expert systems. The measurement of this information is both quantitative and qualitative. Many different senses may be fitted to a single word. The question which arises is how exactly to interpret this inexact information? Fuzzy sets simplify the task of translation between human reasoning and operation of digital computers. Such translations are made by providing the membership function that defines linguistic values - such as "very", "highly", "young", "like", "healthy". This is particularly important in expert systems, where the instructions to be programmed are essentially rules of thumb. In fuzzy logic fuzzy quantifiers are made explicit. A fuzzy quantifier such as "most" may be represented as a fuzzy number, that is, a fuzzy set that defines the degree to which any given proposition matches the definition of "most". The capability to translate concepts such as "usually" in a consistent way would be an advantage Page 70 for expert systems. The translation between human usable linguistic terms and formal languages operators might be expressed by fuzzy numbers, including the context factor and prehistory. The inference process from imprecise or vague premises is becoming more and more important for knowledge-based systems, especially for fuzzy expert systems (see [Mamdani 77], [Yager 84], [Zadeh 75]). In approximate reasoning there are several kinds of inference rules, which deal with the problem of deduction of conclusions in an imprecise setting. 2 Concept Foundation
Fuzzy logic is the tool which gives programs the capability of making an approximate logical deduction from incomplete or imprecise knowledge. The process of inference which is used by linguistic approach is called fuzzy implication. The exact calculation formulas for the compositional rule of inferences, which has the following global scheme (see [Zadeh 75]):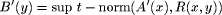 
Global scheme of Generalized Modus Ponens:
Relation: If X is A, Y is B
Observation: X is A'
-------------------
Conclusion: Y is B',
where the membership function of the conclusion Let there be two linguistic variables X and Y defined over the
universe U =  where A and 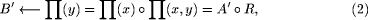 where We assume that we have the input fuzzy information X is Page 71 assume that we are given some inexact (i.e., not crisp) input information, and if we do not take this fact into account, the final inference may be quite different from the real one. One solution to this problem is the defuzzification of fuzzy sets using any of several existing methods. We propose to perform calculations using fuzzy implicit quantifiers which have the possibility of being dynamically described. 3 Method of Fuzzy Quantifiers Description
One of the first attempts at the quantification of word meaning was made by Mosier (1941) in [Hersh and Caramazza 76]. Mosier hypothesized that the meaning of a word may be considered as containing two components: a constant, reflecting the overall meaning value and a variable component representing the variation in the meaning of the word due to context. The method however requires the availability of a simple interpretation of every one case. This requirement is difficult to fulfill in real situations where many of the medical cases for each concrete person will be appearing for the first time. In this case more often than not, there is a vague idea about activity, which must then be estimated subjectively. Facing this situation one solution is offered. The proposed method for the description of fuzzy quantifiers in formal
language involves two steps. The first step is to estimate the context
(dependance from related Data-base), this is C value, which is in
connection with previously quantifier's state Since the grade of membership is both subjective and dependent on context, there is not much point in treating it as a precise number. How then do we calculate the fuzzy quantifier "most", or "usually" in the preposition: "If John is ill, John is in the hospital."? Relation: "If John is ill, John is in the hospital." Observation: "John is ill." ---------------------------------------------- Conclusion: "John is in the hospital." This means "usually" Thus to calculate the implicit fuzzy quantifier in the preposition given above it is proposed to calculate them using the fuzzy numbers in the formula  where In (3) the "+" operation is the fuzzy sum operation, defined by Zadeh 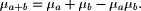 Page 72 We use the product operation given by 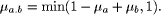 When we use a linguistic term for the first time then we have the following
reduced formula obtained from (3) by ignoring 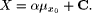 The value X is assumed to be the current value of the fuzzy
quantifier 4 Example Analysis and Comparison with Interpolation Method
Instead of assuming that an ill-known value should be represented by a probability distribution, a fuzzy number may be more appropriate. In general, calculating the membership function is a non-trivial problem. However, in certain cases it is possible to calculate relatively easily. For example, let us consider the fuzzy numbers x = "about 3" and y = "roughly 6", for which the membership functions are triangular. Linear interpolation is valid between the point x = [2 : 0,3 : 1,4 : 0], and the point y=[0 : 0,6 : 1,9 : 0] [see Fig. 1]. We can easily calculate the difference by The resulting membership function is obtained by: 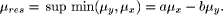 The sum may be calculated in an analogous manner. Multiplication and division are similar, although linear interpolation is no longer valid. Fuzzy numbers are an approximation because data is not known accurately, and we should not calculate results to a greater accuracy than is justified by the original data. The imprecision in an inferred result is greater than the imprecision contained in each premise, just like in error calculus where as soon as computations are performed, imprecision increases. In [Raha and Ray 92] it is demonstrated that instead of inferring by performing approximate reasoning using a relational matrix R formed from a compound proposition p1 and a simple proposition of the form p2: p1 Relation: If X is A then Y is B, p2 Observation: X is A', Page 73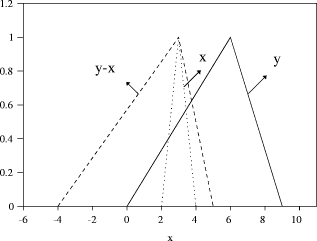 
inferences may also be made by constructing a simple conventional relation of the form y = f(x), a value of Y for a particular value of X. In most cases the output of an approximate reasoning system is defuzzified either conceptually (in case of medical consultancy, etc.) or physically (in case of process control, etc.). In [Raha and Ray 92] it is proposed that instead of defuzzifying the output, we can defuzzify the vagueness of the linguistic statements at the structural level, construct a simple conventional relation that also captures the experience and intuition of an expert, and apply the method of interpolation for inference. But why do not we use the fuzzy number and fuzzy arithmetic appropriate for a given situation? If we do this, we allow the user to build a knowledge base representing the contents of a technical case study. The defuzzifying of information before making any conclusion may be useless in a real-world application. A Fuzzy set, as its name implies, is a class with fuzzy boundaries: the class of small numbers, e.g., old men. Basically the grade of membership is subjective in nature; it is a matter of definition rather than measurement. Humans have a remarkable ability to assign a grade of membership to a given object without a conscious understanding of how the grade is arrived at. A fuzzy quantifier such as "Most" may be represented as a fuzzy number - a fuzzy set that defines the degree to which any given proposition matches the defition of "Most". Thus "Vegetarians are healthy" may really mean "Most vegetarians are healthy". The proportion of fuzzy set elements is represented by the fuzzy quantifier "Most". For example, from the statement: "Usually lean people are vegetarians" and "Most vegetarians are healthy", one could deduce that "usually most lean people are healthy". In this case "usually.most" represents the product Page 74 of fuzzy quantifier "most" and "usually". But this resulting quantifier is less specific than "most" or "usually" in the premises [see Fig. 2]. 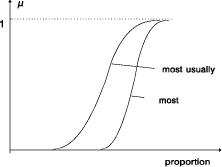 5 Conclusion
In this paper a method for the description of fuzzy quantifiers was discussed. A comparison between fuzzy reasoning and interpolation is made. We have shown that the difficulty in Fuzzy arithmetic arises because of the algebraic structure of fuzzy numbers. We examine a numerical example with a self build convolution for computing with two fuzzy numbers. In the last several years expert systems have emerged as one of the most important applications of Artificial Intelligence. Reflecting human expertise, much of the information in the knowledge base of a typical expert system is imprecise, incomplete, or not totally reliable. For this reason the answer to a question or the advice rendered by an expert system is usually qualified with a "certainty factor", which gives the user an indication of the degree of confidence that the system has in its conclusion. To arrive at the certainty factor, the existing expert systems employ what are essentially probability-based methods. However, since much of the uncertainty in the knowledge base of a typical expert system derives from the fuzziness and incompleteness of data, rather than from its randomness, the computed values of the certainty factor are frequently lacking in reliability. This is still one of the most serious shortcomings of expert systems when the reliability of the conclusions - as in the case of medical diagnostic systems - is of prime importance. Fuzzy logic provides a natural framework for the design of expert systems. The design of expert systems maywell prove to be one of the most important applications of fuzzy logic in knowledge engineering and information technology. The linguistic approach may well prove to be a step in the direction of a lesser preoccupation with exact quantitative analyses, and a greater acceptance Page 75 of the pervasiveness of imprecision in much of human thinking and perception. References
[Hersh and Caramazza 76] Hersh, M., Caramazza, A.: "A Fuzzy Approach to Modifiers and Vagueness in Natural Language"; Journal of Experimental Psychology: General, 105, 3 (1976), 254-276. [Mamdani 77] Mamdani, E. H.: "Application of Fuzzy Logic to Approximate Reasoning Using a Linguistic System"; IEEE Transaction on Computers, C-26, (1977), 1182-1191. [Margrez and Smets 98] Margrez, P., Smets, P.: "Fuzzy Modus Ponens: A New Model Suitable For Application in Knowledge-Based Systems"; Internat. J. Intelligent Systems 4 (1989), 181-200. [Prati 91] Prati, N.: "About the Axiomatizations of Fuzzy Set Theory"; Fuzzy Sets and Systems, 39 (1991), 101-109. [Raha and Ray 92] Raha, S., Ray, K.: "Analogy Between Approximate Reasoning and the Method of Interpolation"; Fuzzy Sets and Systems, 51, 3 (1992), 259-266. [Sudkamp and Hammell 94] Sudkamp, T., Hammell, R.: "Interpolation, Completion, and Learning Fuzzy Rules"; IEEE Transaction on Systems, Man and Cybernetics, 24, 2 (1994), 332-342. [Tanaka 86] Tanaka, K.: "Conclusions From a Consideration of the Uncertainty Factor and Vagueness in Engineering Art"; in Yager (Eds.) Fuzzy Sets and Possibility Theory-Recent Achievements; (1986), 37-50 (in Russian). [Wood, Antonsson and Beck 90] Wood, K. L., Antonsson, E. K., Beck, J. L.: "Representing Imprecision in Engineering Design: Comparisons of Fuzzy and Probability Calculus"; Res. in Engineering Design 1 (1990), 187-203. [Yager 84] Yager, R. R.: "Approximate Reasoning as a Basis for Rule-Based Expert Systems"; IEEE Transaction on Systems, Man and Cybernetics, 14 (1984), 636-643. [Zadeh 84] Zadeh, L. A.: "Making Computers Think Like People"; IEEE Spectrum, Aug. (1984), 26-32. [Zadeh 75] Zadeh, L. A.: "The Concept of a Linguistic Variable and its Application to Approximate Reasoning-III"; Inf. Sciences, 9, 1 (1975), 43-80. [Yager 86] Yager, R. (Ed.): "Fuzzy Sets and Possibility Theory-Recent Achievements"; Radio and Connection, Moscow (1986) (in Russian). Page 76
|
|||||||||||||||||
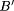is defined by some
sup-t-norm composition of 
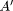and relation matrix R.
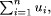and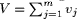 
, respectively, and let us consider the two
propositions p1 and p2, expressed in natural language. Also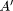
are fuzzy
subsets over U, B is a fuzzy subset over V and the relation R is a
fuzzy subset of the Cartesian product U x V. The fuzzy implication (1)
is chosen by some user defined approach. Using the compositional rule
of inference we obtain
denotes the well known max-min composition operator.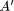
. Then the fuzzy expert system may
infer that Y is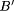 
by
(2). Let there be n fuzzy implications of type (1) which specify the
rule in some system. The final inference may be Y is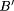 
as result of
separate rule based computing and their consequent union. If we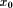
. The second step gives
the calculated value of this quantifier used at the current moment. We
then obtain the meaning value of the current fuzzy number
(quantitative measurement) from the sum of the results of the first
and second steps.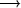
with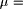 
0.6, membership grade in which the "usually"
may be translated.
and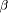 
are parametric components, over people; 
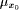is the membership
function value against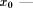 
previously x; 
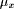is the current value of the fuzzy
quantifier, and C is a context dependant value in the interval [0,1].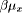
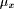, and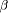 
is a weight coefficient which indicates how many times
it was used. The algorithm for calculating the fuzzy quantifier is
dynamic and in each subsequent consideration of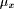 
, the value of 
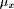is
altered. Thus, in the end we have a calculated value for a fuzzy number
that implies the context, the prehistory and the recursive accumulated
use of such linguistic terms. How then do we calculate with fuzzy
numbers? This is matter of deffinition and furthermore assumes that the
interpretation of connectives in fuzzy logic is generally
context-dependent rather than universal. Following [
