(D. Lester) Exact Statistics and Continued Fractions

Abstract: In this paper we investigate an extension to Vuillemin's work on continued fraction arithmetic [Vuillemin 87, Vuillemin 88, Vuillemin 90], that permits it to evaluate the standard statistical distribution functions. By this we mean: the normal distribution, the 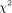-distribution, the t-distribution, and, in particular, the F-distribution. The underlying representation of non-rational computable real numbers is also as continued fractions, in the style of Vuillemin. This permits arbitrary accuracy over a range of values. The number of terms of a continued fraction that are used by the implementation is dynamically controlled by the accuracy demanded of the final answer. The use of a modern lazy functional language - Haskell - has considerably eased the programming task. Two features are of note. Firstly, the type-class structure allows one to augment the varieties of numbers supported by the language. Secondly, the laziness inherent in the Haskell's semantics, makes it very straightforward to dynamically control the accuracy of the intermediate evaluations.