| Submission Procedure |
On Four Classes of Lindenmayerian Power Series
Department of Mathematics University of Turku SF-20500 Turku, Finland juha.honkala@utu.fi Institut fuer Algebra und Diskrete Mathematik Technische Universitaet Wien Wiedner Hauptstrasse 8-10, A-1040 Wien Abstract: We show that nonzero axioms add to the generative capacity of Lindenmayerian series generating systems. On the other hand, if nonzero axioms are allowed, nonterminals do not, provided that only quasiregular series are considered. Category: F.4.2 1 Introduction
To define formal power series generated by L systems,
Lindenmayerian series generating systems were introduced in
[Honkala 95]. There four classes of morphically generated series were
defined. The smallest class The inclusions Another approach to define a power series generalization of L systems is given in [Kuich 94]. For the relationship between the two approaches see [Honkala and Kuich 95]. In the case of a complete semiring, power series generalizations of L systems are also discussed in [Honkala 94a] and [Honkala and Kuich 00]. 2 Definitions
It is assumed that the reader is familiar with the basics of the theories of semirings and formal power series as developed in [Kuich and Salomaa 86]. In this Page 131 paper A will always be a commutative semiring and
by
Notice that the assumption of commutativeness is needed in the
verification that indeed
In what follows X is a denumerably infinite alphabet of
variables. An interpretation The series generated by an LS system is obtained by iteration.
Suppose
If
and say that S(G) is the series generated by G. The sequence
A series r is called an ELS series if there exists an
ELS system G
such that r = S(G). A series r is called an ELS series with the
zero axiom if there exists an ELS system If A and In the sequel we will always use the convergence Page 132 3 Results
The purpose of this section is to prove the following result. Theorem 1. (i) If A is a commutative semiring and (ii) If A = N, then Lemma 2.
Suppose
Proof. We assume without loss of generality that each term of the approximation sequence Choose new letters
Define the LS system
and
for
Now the claim follows by renaming the letters. Page 133 In the proof of Lemma 2 the letters of Next we recall some earlier results. Lemma 3
Let A = N and denote Proof. The claim is shown in Examples 3.6 and 4.3 of [Honkala 95]. Lemma 4
Let A = N. Then the series Proof. See [Honkala 94b]. For the next lemma we need a definition. A vector of LS
systems of dimension
and say that The next lemma is stated and proved as Theorem 4.5 in [Honkala 95]. Lemma 5.
Lemma 6.
Proof. Denote
where
Page 134
Proof of Theorem 1. Claim (i) follows by Lemma 2. Claim (ii) is a consequence of Lemmas 3,4 and 6. References
[Honkala 94a] Honkala, J.: 'On Lindenmayerian series in complete semirings'; In G. Rozenberg and A. Salomaa, eds., Developments in Language Theory (World Scientific, Singapore, 1994) 179-192. [Honkala 94b] Honkala, J.: 'An iteration property of Lindenmayerian power series'; In J. Karhumaki, H. Maurer and G. Rozenberg, eds., Results and Trends in Theoretical Computer Science (Springer, Berlin, 1994) 159-168. [Honkala 95] Honkala, J.: 'On morphically generated formal power series'; Rairo, Theoretical Inform. and Appl., to appear. [Honkala and Kuich 95] Honkala, J. and Kuich, W.: 'On a power series generalization of ET0L languages'; Fundamenta Informaticae, to appear. [Honkala and Kuich 00] Honkala, J. and Kuich, W.: 'On Lindenmayerian algebraic power series', submitted. [Kuich 94] Kuich, W.: 'Lindenmayer systems generalized to formal power series and their growth functions'; In G. Rozenberg and A. Salomaa, eds., Developments in Language Theory (World Scientific, Singapore, 1994) 171-178. [Kuich and Salomaa 86] Kuich, W. and Salomaa, A.: 'Semirings, Automata, Languages'; Springer, Berlin (1986).
Page 135
|
|||||||||||||||||
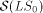 consists of LS
series with the zero axiom. The larger class
consists of LS
series with the zero axiom. The larger class 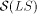 is
obtained if arbitrary axioms are allowed. From these classes the
classes
is
obtained if arbitrary axioms are allowed. From these classes the
classes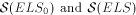 of ELS series
with the zero axiom and ELS series, respectively, are obtained
by allowing the use of Hadamard products. In an obvious way this
corresponds to the use of nonterminals in language theory.
of ELS series
with the zero axiom and ELS series, respectively, are obtained
by allowing the use of Hadamard products. In an obvious way this
corresponds to the use of nonterminals in language theory.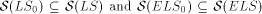 are clear by
the definitions. It was shown in [
are clear by
the definitions. It was shown in [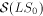 is
properly contained in
is
properly contained in 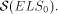 Hence, in the case of the zero
axiom nonterminals do add to the generative capacity. The purpose
of this note is to prove that
Hence, in the case of the zero
axiom nonterminals do add to the generative capacity. The purpose
of this note is to prove that 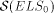 is properly contained in
is properly contained in
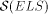 and, furthermore, that the classes
and, furthermore, that the classes
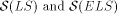 are
equivalent, if only quasiregular power series are considered.
Hence, nonzero axioms do add to the generative capacity whereas,
if nonzero axioms are allowed, nonterminals do not. However, it
will be seen below that in the framework of Lindenmayerian series
with nonzero axioms some terminals play the role of nonterminals.
are
equivalent, if only quasiregular power series are considered.
Hence, nonzero axioms do add to the generative capacity whereas,
if nonzero axioms are allowed, nonterminals do not. However, it
will be seen below that in the framework of Lindenmayerian series
with nonzero axioms some terminals play the role of nonterminals.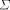 is
a finite alphabet. Suppose
is
a finite alphabet. Suppose 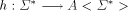 is a monoid morphism.
(Here
is a monoid morphism.
(Here 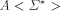 is regarded as a multiplicative
monoid.) Then we extend h to a semiring morphism
is regarded as a multiplicative
monoid.) Then we extend h to a semiring morphism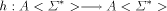
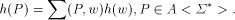
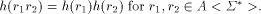 In the sequel we always tacitly extend a morphism
In the sequel we always tacitly extend a morphism
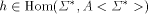 to a semiring morphism
to a semiring morphism 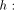
 as explained above. Notice
as explained above. Notice 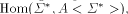 that the set of all these
semiring morphisms, can be identified with the set
that the set of all these
semiring morphisms, can be identified with the set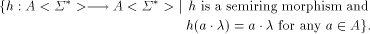

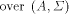 is a
mapping from X to
is a
mapping from X to 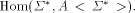 A Lindenmayerian series generating system, shortly,
an LS system, is a 5-tuple
A Lindenmayerian series generating system, shortly,
an LS system, is a 5-tuple 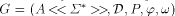 where A is a commutative semiring,
where A is a commutative semiring, 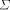 is a finite alphabet,
is a finite alphabet, 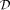 is a convergence
in
is a convergence
in 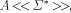 P is a polynomial in
P is a polynomial in 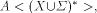
 is an
interpretation over
is an
interpretation over 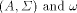 is a polynomial in
is a polynomial in 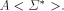
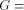
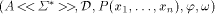 is an LS system and
denote
is an LS system and
denote 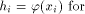
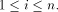 Define the sequence
Define the sequence
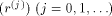 recursively by
recursively by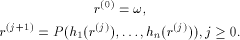
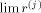 exists we denote
exists we denote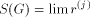
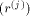 is the approximation sequence associated to G.
A series r
is called an LS series if there exists an LS system G such
that r = S(G). A series r is an LS series with the zero axiom if there
exists an LS system
is the approximation sequence associated to G.
A series r
is called an LS series if there exists an LS system G such
that r = S(G). A series r is an LS series with the zero axiom if there
exists an LS system
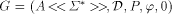 such
that r = S(G). ELS series are obtained from LS series by
considering only
terms over a terminal alphabet. Formally, an ELS system is a
construct
such
that r = S(G). ELS series are obtained from LS series by
considering only
terms over a terminal alphabet. Formally, an ELS system is a
construct 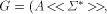
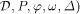 consisting of the LS system
consisting of the LS system
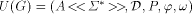 called the underlying system of G and a subset
called the underlying system of G and a subset 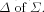 If S(U(G)) exists, G
generates the series
If S(U(G)) exists, G
generates the series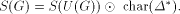
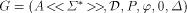 such that r = S(G).
such that r = S(G).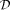 are understood, the class of LS series with the zero
axiom (resp. LS series, ELS series with the zero axiom, ELS
series) is denoted by
are understood, the class of LS series with the zero
axiom (resp. LS series, ELS series with the zero axiom, ELS
series) is denoted by 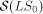 (resp.
(resp. 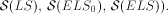
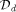 obtained by
transferring the discrete convergence in A to
obtained by
transferring the discrete convergence in A to 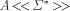 as explained in [
as explained in [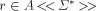 is quasiregular, then
is quasiregular, then 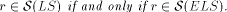
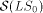 is properly included in
is properly included in 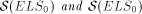 is properly included in
is properly included in 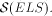
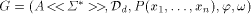 is an LS
system such that S(G) exists and is quasiregular. If
is an LS
system such that S(G) exists and is quasiregular. If 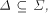 then there exists an LS system
then there exists an LS system 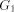 such that
such that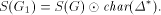
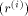 of G is quasiregular.
of G is quasiregular.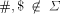 and new
variables
and new
variables 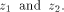 Let
Let 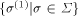 be an isomorphic copy of
be an isomorphic copy of 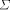 and let
and let 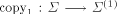 be the mapping defined by
be the mapping defined by 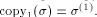 Denote and each term of
Denote and each term of 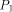 contains
a variable.
Define
contains
a variable.
Define 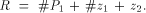 If
If
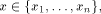 define
define 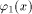 by
by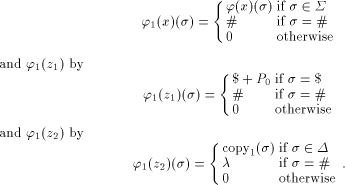
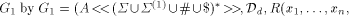
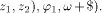 Denote the approximation sequence
associated to
Denote the approximation sequence
associated to 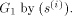 It follows inductively that there
exists a sequence
It follows inductively that there
exists a sequence 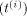 such that
such that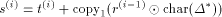
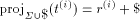
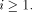 Furthermore, each word in
Furthermore, each word in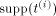 contains at least i occurrences of #. (Here the morphism
contains at least i occurrences of #. (Here the morphism
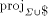 is defined by
is defined by
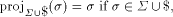 and
and 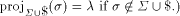 This implies
This implies 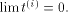 Therefore
Therefore 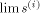 exists and
exists and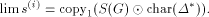
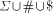 play
the role of
nonterminals. However, because
play
the role of
nonterminals. However, because 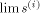 does not contain any
letters of
does not contain any
letters of 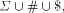 we do not need the Hadamard product.
we do not need the Hadamard product.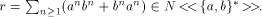
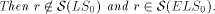
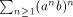 does not
belong to
does not
belong to 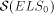 .
.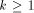 is a k-tuple
is a k-tuple 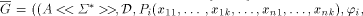
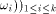 of LS systems. The approximation sequence
of LS systems. The approximation sequence 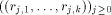 associated to G is defined recursively by
associated to G is defined recursively by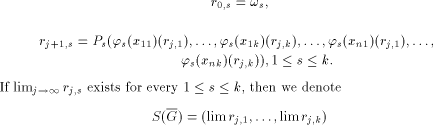
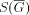 is the ( vector of) series generated by
is the ( vector of) series generated by 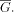
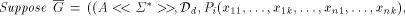
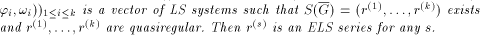
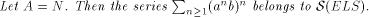
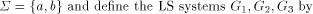
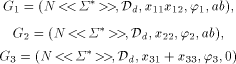
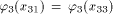 is the identity morphism and
is the identity morphism and 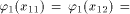
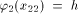 is defined by h(a) = a,h(b) = ab.
Furthermore, define the 3-dimensional vector
is defined by h(a) = a,h(b) = ab.
Furthermore, define the 3-dimensional vector 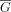 of LS systems by
of LS systems by 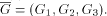 Denote by
Denote by 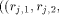
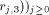 the approximation sequence of
the approximation sequence of 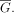 Then
Then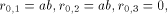
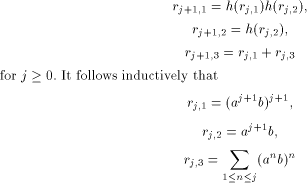
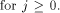 Therefore
Therefore 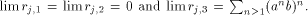 Hence
Hence 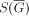 exists and each component of
exists and each component of 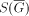 is quasiregular. Therefore the claim follows by Lemma 5.
is quasiregular. Therefore the claim follows by Lemma 5.