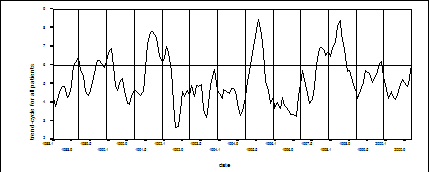
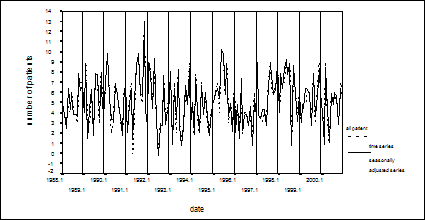
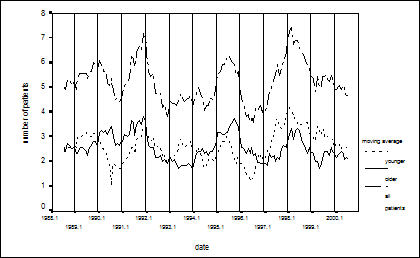
Analysing Data of Childhood Acute Lymphoid Leukaemia by Seasonal Time Series Methods

Abstract: We examined the periodicity of the childhood leukaemia in Hungary using seasonal decomposition time series. Between 1988 and 2000 the number of annually diagnosed leukaemia (incidence) was analysed. The time series of the number of patients between the age of 0 and 18 years and the data series divided at the median were analysed. From the time series the seasonal components, trends, the seasonally adjusted series, the moving averages and the data series of the random components were examined. The seasonal components of the dates of diagnosis revealed that a higher percent of the peaks fell within the winter months than in the other seasons. This proves the seasonal occurrence of the childhood leukaemia in Hungary. These data seem to highlight the role of the environmental effects (viral infections, epidemics, etc.) on the onset of the disease.

Keywords: time series analysis, seasonal decomposition time series method, acute childhood lymphoid leukaemia

Category: G

1 Introduction

The method of seasonal time series analysis can be used in various fields of the medicine. With such time series one can detect the periodic trend of the occurrence of a certain disease [Barnett-Dobson, 2004], [Cani et al., 2001], [Fleming et al. 2000], [Gallerani et al., 2004], [Oberg et al., 2000], [Pereira, 2004], [Saynajakangas et al., 2001]. Among other diseases, the seasonal periodicity of the childhood lymphoid leukaemia was also analysed using statistical methods [Cohen, 1987], [Harris-Harrel, 1987], [Meltzer et al., 1996], [Sorenson-Pedersen, 2001], [Vienna-Polan, 1976]. The importance of this theme was indicated that in the last few years in many international publications were discussed with the seasonal variations of childhood leukemia/lymphoma and the acute lymphoblastic leukemia [Karimi-Yarmohammadi, 2005], [Gao et al., 2005].

The pathogenesis of the childhood lymphoid leukaemia is still uncertain, but certain environmental effects may provoke the manifestation of latent genes during viral infections, epidemics or pregnancy.

The date of the diagnosis of patients were statistically analysed to determine the role, which the accumulating viral infections and other environmental effects may play during the conception and fetal period on the manifestation of the disease. Because the available data is rather limited and controversial, it seemed logical to make an in-depth analysis of the date of diagnosis of the acute lymphoid leukaemia in Hungarian children.

2 Methods

The databank of the Hungarian Paediatric Oncology Workgroup contains the data of all the patients with lymphoid leukaemia diagnosed between 1988 and 2000. In this time interval a total of 814 children were registered (of which 467 were boys). The patients were 0-18 years old, with a mean age of 6,4 years and a median of 5,4 years. The components of the time series can be identified and isolated using mentioned statistical program packages.

The periodicity of acute childhood lymphoid leukaemia in Hungary was examined using seasonal decomposition time series method.

2.1 Seasonal Time Series

Time series consist of three components: the trend, the periodicity and the random effects. The trend is a long-term movement representing the main direction of changes. The periodicity marks cyclic fluctuations within the time series. The irregularity of the peaks and drops form a more-or-less constant pattern around the trend line. Due this stability the length and the amplitude of the seasonal changes is constant or changes very slowly. If the periodic fluctuation pattern is stable, it is called a constant periodic fluctuation. When the pattern changes slowly and regularly over the time, we speak of a changing periodicity. The third component of the time series is the random error causing irregular, unpredictable, non-systematic fluctuations in the data independent from the trend line.

An important part of the time series analysis is the identification and isolation of the time series components. One might ask how these components come together and how can we define the connection between the time series and its components with a mathematical formula. The relationship between the components of a time series can be described either with an additive or a multiplicative model.

Let y_i,j (i=1, ... , n; j=1, ... , m) marks the observed value of the time series. The index i stand for the time interval (i.e. a year), the j stands for a particular period in the time interval (i.e. a month of the year). By breaking down the time series based on the time intervals and the periods we get a matrix-like table. In the rows of the matrix are the values from the various periods of the same time interval; while in the columns are the values from the same periods over various time intervals.

y_1,1; y_1,2; ... ; y_1,m;
y_2,1; y_2,2; ... ; y_2,m;
y_3;1; y_3,2; ... ; y_3,m;
...
y_n,1; y_n,2; ... ; y_n,m .

Let d_i,j (i=1,2, ... , n; j=1,2, ... , m) mark the trend of the time series, s_i,j (i=1,2, ... , n; j=1,2, ... , m), the periodic fluctuation and ε_i,j (i=1,2, ... , n; j=1,2, ... , m), the random error. Using these denotations the additive seasonal model can be defined as y_i,j=d_i,j+s_i,j+ε_i,j; (i=1,2, ... , n; j=1,2, ... , m); the multiplicative model as y_i,j=d_i,j*s_i,j*ε_i,j; (i=1,2, ... , n; j=1,2, ... , m).

The trend of a time series can easily be computed with moving averages or analytic trend calculation. Moving averaging generates the trend as the dynamic average of the time series. Analytic trend calculation approximates the long-term movement in the time series with a simple curve (linear, parabolic or exponential curve) and estimates its parameters.

The indices of the periodic fluctuation are called seasonal differences (in the additive model) or seasonal ratios (in the multiplicative model). These indices represent the absolute difference from the average of the time interval using the additive model or the percentile difference using the multiplicative model. Seasonal adjustment is done by subtracting the j seasonal difference from the j data value of each i season (additive model) or by dividing the j data value of each i season by the j seasonal ratio (multiplicative model). The seasonally adjusted data reflect only the effect of the trend and the random error.

3 Results

The components of the time series can be identified and isolated using statistical program packages. The analysis of the seasonal periodicity of the childhood leukaemia was done with the Seasonal Decomposition module of the SPSS/PC+ statistical program package.

3.1 Analysing the Periodicity of Acute Childhood Lymphoid Leukaemia

The analysis of the periodicity of acute childhood lymphoid leukaemia was performed on the basis of the date of the diagnosis (year and month) of the disease (monthly incidence). We analysed three data series. The first data series contained the number of all the patients diagnosed monthly, the second contained the number of those patients younger than the value of the median, the third contained the number those older than the value of the median.

The seasonal components of all patients revealed 9 peaks. 6 of these peaks fell within the winter months, 1 in the autumn period, 1 in the summer months, 1 in the spring months (Figure 1.). The seasonal components of the younger age group showed 7 peaks in the winter, 1 in the spring and 1 in the summer months. The seasonal components of the older age group showed 7 peaks in the winter, 1 in the spring, 1 in the autumn and 4 in the summer months.

Figure 1: Seasonal components of all patients of acute lymphoid leukaemia diagnosed monthly in the observed period. Peaks of seasonal components show the seasonal occurrence of the childhood leukaemia mainly in winter months.

Figure 2 shows the number of all patients (incidence) and the seasonally adjusted series.

Figure 3 shows the moving average (window width =12 months) of the number have diagnosed cases of childhood leukaemia for three age groups.

Figure 3: Moving averages calculated for three groups (younger than the value of the median, older than the value of the median, and all patients) of patients with childhood leukaemia

4 Conclusions

Analysis of the seasonality of childhood lymphoid leukaemia in Hungary was performed both on the total number of patients and on the data series divided at the median. A certain periodicity was found in the dates of the diagnosis in patients with leukaemia. Although there was some difference in the patterns of the seasonal components peaks of the three time series, the majority of the peaks fell within the winter months in all three time series. This was more significant in the group of all the patients and in the younger age group. The results of the analyses proved the seasonal occurrence of the childhood lymphoid leukaemia in Hungary. These results refer to that in winter months certain environmental effects, suspected viral infections, may provoke the manifestation of disease.

Some studies reported similar seasonality [Vienna-Polan, 1976], while other studies denied any kind such periodicity [Sorenson-Pedersen, 2001]. Similarly our data in occurrence of childhood leukaemia (incidence) an autumn-winter peak were established by Karimi and Yarmohammadi [Karimi-Yarmohammadi, 2003], but they underlined the problem is complex and need more definitive studies. On the other hand Gao and collaborators were examined the seasonality of acute lymphoblastic leukaemia in different geographic locations. No seasonal pattern was found in Singapore, in Hawaii and in USA. In contrast, a significant peak (early January) was observed for western Sweden. On the basis of examinations they were concluded there is little evidence of any seasonality in the diagnosis of acute lymploblastic leukaemia [Gao et al., 2005].

Due to the controversial nature of the available international data, further studies should be carried out.

Acknowledgements

Statistical data are courtesy of Prof. Pál Kajtár, head of the Hungarian Paediatric Oncology Workgroup.

References

[Barnett and Dobson, 2004] Barnett, A.G., Dobson, A.J.: Estimating trends and seasonality in coronary heart disease, Stat Med 2004, 23 3505-3523.

[Cani et al., 2001] Cani, L., Rios M., Sanchez J.: Meningococcal disease in Spain: seasonal nature and resent changers, Gac Sanit 2001, 15(4) 336-340.

[Cohen, 1987] Cohen, P.: The influence on survival of onset of childhood acute leukaemia (ALL), Chronobiol Int 1987, 4 291-297.

[Fleming et al. 2000] Fleming D.M., Cross K.W., Sunderland R., Ross A.M.: Comparison of the seasonal pattern of asthma identified in general practitioner episodes, hospital admissions and deaths, Thorax 2000, 8 662-665.

[Gallerani et al., 2004] Gallerani, M., Boari, B., de Toma, D., Salmi, R., Manfredini, R.: Seasonal variation in the occurrence of deep vein thrombosis, Med Sci Monit 2004, 10 191-196.

[Gao et al., 2005] Gao, F., Nordin, P., Krantz, I., Machin, D.: Variation inthe seasonal diagnosis of acute lymphoblastic leukaemia: Evidence from Singapore, the United States, and Sweden, American Journal of epidemiology 2005, 162(8) 753-763.

[Harris-Harrel, 1987] Harris, R.E., Harrel, F.E., Patil, K.D., Al-Rashid, R.: The seasonal risk of paediatric/childhood acute lymphocyte leukaemia in the United States, J Chronic Dis 1987, 40 915-923.

[Karimi-Yarmohammadi, 2003] Karimi, M., Yarmohammadi, H.: Seasonal variations in the onset of childhood leukaemia/lymphoma: April 1996 to march 2000, Shiraz, Iran, Haematological Oncology 2003, 21(2) 51-55.

[Meltzer et al., 1996] Meltzer, A. A., Annegers, J. F., Spitz, M. R.: Month-of-birth and Incidence of Acute Lymphoblastic Leukaemia in Children, Leuk Lymph 1996, 23 85-92.

[Oberg et al., 2000] Oberg A.L., Ferguson J.A., McIntrre L.M., Horner R.D.: Incidence of stroke and season of the year: evidence of an association, Am J Epidemiol 2000, 152(6) 558-564.

[Pereira, 2004] Pereira, A.: Performance of time series methods in forecasting the demand for red blood cell transfusion, Transfusion 2004, 44 739-746.

[Saynajakangas et al., 01] Saynajakangas P., Keistinen T., Tuuponen T.: Seasonal fluctuations in hospitalisation for pneumonia in Finland, Int J Circumpolar Health 2001, 60(1) 34-40.

[Sorenson-Pedersen, 2001] Sorenson, H.T., Pedersen, L., Olse, J.H., et al.: Seasonal variation in month of birth and diagnosis of early childhood acute lymphoblastic leukaemia, Journal of the American Medical Association 2001, 285(2) 168-169.

[Vienna-Polan, 1976] Vienna, N.J., Polan, A.K.: Childhood lymphatic leukaemia prenatal seasonality and possible association with congenital Varicella, Am J Epidemiol 1976, 103 321-332.