| Submission Procedure |
Finding Plagiarisms among a Set of Programs with JPlagLutz Prechelt Guido Malpohl Michael Philippsen Abstract: JPlag is a web service that finds pairs of similar programs among a given set of programs. It has successfully been used in practice for detecting plagiarisms among student Java program submissions. Support for the languages C, C++ and Scheme is also available. We describe JPlag's architecture and its comparsion algorithm, which is based on a known one called Greedy String Tiling. Then, the contribution of this paper is threefold: First, an evaluation of JPlag's performance on several rather different sets of Java programs shows that JPlag is very hard to deceive. More than 90 percent of the 77 plagiarisms within our various benchmark program sets are reliably detected and a majority of the others at least raise suspicion. The run time is just a few seconds for submissions of 100 programs of several hundred lines each. Second, a parameter study shows that the approach is fairly robust with respect to its configuration parameters. Third, we study the kinds of attempts used for disguising plagiarisms, their frequency, and their success. Key Words: plagiarism, similarity, search, token, string tiling Categores: GT algorithms, GT performance, F.2.2. pattern matching, H.3.3., H.5.2., I.5.4. text processing, K.3.m., K.5.1 1 Detecting similar programsMillions of programming exercises are being turned in by students each year. In most cases, their instructors have the uneasy feeling that a few of these programs are more or less copies of programs supplied by somebody else who is taking the same course at the same time. We call such copies plagiarisms . Very few instructors have the patience to thoroughly search for plagiarisms; although finding plagiarisms is possible, it is much too timeconsuming in practice. If any, instructors find duplicates only by accident, e.g., if a student has forgotten to replace the name of the friend in the head of the program source text or if two programs produce the same weird failure for a test input. A powerful automated search that finds similar pairs among a set of programs would be most helpful - if, and only if, that search can discriminate well enough between incidental similarities and actual plagiarisms. 1.1 JPlagWe have built such a system, called JPlag. It is written in Java and currently analyzes program source text written in Java, Scheme, C, or C++. Page 1016 We will consider only the Java mode here. JPlag is publicly available at http://www.jplag.de. As of fall 2001, JPlag processes several dozen submissions each month. We and JPlag users from other institutions have used it very successfully in courses at both undergraduate and graduate level, some submissions having as many as 500 participants. JPlag takes as input a set of programs, compares these programs pairwise (computing for each pair a total similarity value and a set of similarity regions), and provides as output a set of HTML pages that allow for exploring and understanding the similarities found in detail. JPlag converts each program into a string of canonical tokens. For the comparison of two programs, JPlag then covers one such token string by substrings taken from the other (string tiling) where possible. 1.2 Related workSeveral systems finding plagiarisms have been build before. Early attempts at plagiarism detection were usually based on the notion of a feature vector. These systems compute for each program n different software metrics (anywhere from 4 to several dozen), so that each program is mapped to a point in an ndimensional cartesian space. The systems then consider sets of programs that lie close to each other to be possible plagiarisms [Ottenstein, 1976; Donaldson et al., 1981; Grier, 1981; Berghel and Sallach, 1984; Faidhi and Robinson, 1987]. Unfortunately, this approach is at best moderately successful [Verco and Wise, 1996] , because summing up a metric across the whole program throws away too much structural information. Such systems are either very insensitive (and hence easy to fool) or they are sensitive and come up with a large fraction of false positives. This deficiency cannot be removed by adding further dimensions to the comparison. With much more powerful computers the direct comparison of program structure instead of just summary indicators became viable. Some of these systems are hybrids between structure and metric comparison, e.g. [Donaldson et al., 1981; Jankowitz, 1988], others (such as JPlag) rely on structure comparison alone. In the latter case, the approach is usually to convert the program into a string of tokens (thus ignoring easily changeable information such as indentation, line breaks, comments etc.) and then comparing these token strings to find common segments. The most advanced other systems in terms of their plagiarism detection performance are probably YAP3 [Wise, 1992] and MOSS [Aiken, 1998]. JPlag uses the same basic comparison algorithm as YAP3, but uses a different set of optimizations for improving its run time efficiency. MOSS uses a slightly different approach1 for even higher speed at the cost of some detection performance and is able to ignore base code that is expected in almost all submissions. JPlag introduces a unique user interface for presenting the set of similar regions for two programs. This interface then inspired a similar one for MOSS. [Cluwin et al., 2001] attempted a comparison of MOSS and JPlag, but unfortunately chose a program set that contained a fraction of identical base code in all submissions, which is handled very differently by MOSS compared to JPlag, yet the authors failed to provide a manual check of the quality of the two systems' output. 1Personal communication with Alex Aiken. No written description of MOSS's internals is available. Page 1017 The core part of the present study is its careful evaluation of JPlag's performance and also a direct comparison to MOSS. Although several performance studies such as [Verco and Wise, 1996; Whale, 1990; Wise, 1992] exist for earlier systems, these studies are fairly restricted both with respect to the quality and amount of the input data used and in the level of detail of the evaluation itself. 1.3 Structure of the articleSection 2 describes the JPlag system: its appearance as a web service, the GUI by which it presents its search results, and the basic comparison algorithm with its optimizations. Section 3 presents an empirical evaluation of JPlag on four real sets of student programs and on sets of plagiarisms specifically created to deceive such a plagiarism search. The evaluation comprises measurements of the discrimination performance as well as a study of the sensitivity of the algorithm's free parameters. Section 4 analyses the camouflaging strategies used by plagiarists. We arrange them into similar groups, count their frequency, and describe their effectiveness (or more often lack thereof). Additional detail is given in [Prechelt et al., 2000]. 2 The JPlag system2.1 The JPlag WWW serviceAfter logging into the web service with user name and password, a JPlag user submits a directory of files to JPlag for analysis. Each subdirectory's contents supply one program, consisting of one or more source files. JPlag compares the programs and produces a directory of HTML files as output. The submitter (but no other JPlag user) can either view these files online or download them for local use. For the submitted programs, JPlag generates a set of HTML pages that present the results. At the top level, an overview page presents a histogram of the similarity values found for all program pairs and a list of the highestsimilarity pairs. Given the histogram, one usually can identify a range of similarity values that doubtless represent plagiarisms and a range of values which doubtless represent nonplagiarisms. The program pairs that have similarities in between those ranges should be investigated further by hand. JPlag supports such investigations by a unique user interface. For each program pair selected by the user, a sidebyside comparison of the source codes is then shown (see Figure 1 for a partial example). Ranges of lines that have been found to be corresponding in both files are marked with the same color. A hyperlink arrow at each region, when clicked, aligns the opposite half of the display such that the corresponding region is shown. Likewise, one can jump to each pair of corresponding regions from a table shown at the top which lists for each region its color code, position in each of the files, and length in tokens. This unique presentation makes it easy to judge whether or to which degree the pair of programs should in fact be considered plagiarized. For instance it will quickly become clear if the two programmers have shared some parts of the program but created the rest independently or if plagiarized program parts were camouflaged by artificial changes. Page 1018 Figure 1: Part of a JPlag results display page for a pair of programs Page 1019
2.2 JPlag's comparison algorithmThis section describes how JPlag computes the similarity of a pair of programs. JPlag operates in two phases:
2.2.1 Converting the programs into token stringsThe frontend process of converting the programs into token strings is the only languagedependent process in JPlag. Three frontend implementations currently exist: The ones for Java and for Scheme both implement a full parser. The third frontend for C++ (or C) consists of only a scanner. As a rule, tokens should be chosen such that they characterize the essence of a program's structure (which is difficult to change by a plagiarist) rather than surface aspects. JPlag ignores whitespace, comments, and the names of identifiers. Moreover, JPlag puts semantic information into tokens where possible in order to reduce spurious substring matches that can occur by pure chance. For instance in Java, we use a BEGIN_METHOD token instead of just an OPEN_BRACE token. Parserbased front ends are superior in this respect. See Table 1 for a Java example. See Section 4 for understanding the rationale for the tokenization approach. Our evaluation in Section 3.4 suggests that JPlag is fairly robust against changes of the token set. Page 1020 0 GreedyStringTiling(String A, String
B) { Table 2: The "Greedy String Tiling" algorithm
[Wise, 1993]. The 2.2.2 Comparing two token stringsThe algorithm used to compare two token strings is essentially "Greedy String Tiling" [Wise, 1993] . When comparing two strings A and B, the aim is to find a maximal set of contiguous substrings that have the following properties: each substring occurs in both A and B, is as long as possible and does not cover a token already covered by some other substring. To avoid spurious matches, a minimum match length M is enforced. "Greedy String Tiling" is a heuristic algorithm, because guaranteeing maximality for the set of substrings found makes the search too expensive. Here is the rough sketch (see Table 2 for the pseudocode). The algorithm iterates the following two steps: Step 1 (lines 5-18): The two strings are searched for the biggest contiguous matches. Conceptually, this is done by 3 nested loops: The first one iterates over all the tokens in A, the second one compares the current token with every token in B. If they are identical, the innermost loop searches for the end of the match. These nested loops collect the set of all longest common substrings. Page 1021 Step 2 (lines 19-25): Mark all nonoverlapping matches of maximal length found in Step 1. This means that all their tokens are marked and thus may not be used for further matches in Step 1 of a subsequent iteration. In the terminology of Wise, by marking all the tokens a match becomes a tile. These two steps are repeated until no further matches are found. Since
further tokens are marked in each step, the algorithm always terminates.
It returns a list of tiles from which we need to compute a similarity measure.
This measure should reflect the fraction of tokens from the original programs
that are covered by matches. We define it as sim(A, B)
= 2 · coverage(tiles)/(|A| + |B|) where
coverage(tiles) = The run time complexity of this heuristic algorithm is still fairly
high. In the worst case, all three nested loops are executed to their fullest.
Despite the decreasing match length in later iterations this can lead to
a number of steps as large as 2.2.3 Wise's and JPlag's run time optimizationsAlthough the worst case complexity can not be reduced, the average complexity
for practical cases can be improved to almost The KarpRabin algorithm finds all occurrences of a short string (the "pattern" P ) in a longer string (the "text" T ) by using a hash function. To do that, the hash values of all substrings with length |P | in T are calculated. This can be done in linear time by using a hash function h that is able to compute the value of h(TtTt+1 ..Tt+|P|-1 ) from the values of h(Tt-1Tt ..Tt+|P|-2), Tt-1 and Tt+|P|-1. All the hash values are then compared with the value of P. If two values are the same, a characterwise comparison takes place to verify that an occurrence of P in T has been found. The complexity of this algorithm in practice is almost linear. Our modification of Wise's Greedy String Tiling applies the basic idea of KarpRabin matching in the following manner:
The worst case complexity of this algorithm is still Page 1022 JPlag does all the hash computations (hash values of both strings plus hash table for string B) upfront, i.e., only once before the tiling process. When a match is found and a tile is marked, the corresponding entries in the static hash table are no longer valid for subsequent iterations. Since JPlag leaves the affected entries in the table, the verification substep (number 2 above) becomes somewhat more complicated. In contrast, Wise recalculates all the hash values and the hash table in each iteration, so that any match found will be valid.2 Of these two approaches, we found the static precomputation plus the slightly more costly validity checks to be faster for JPlag's default parameters and typical token strings. 3 Evaluation of the JPlag systemIn this section we will investigate JPlag's discrimination performance and its sensitivity to program structure, frequency of plagiarisms, and the free parameters of the JPlag algorithm. We present an empirical study based on several sets of real student programs plus a number of explicitly made plagiarisms. 3.1 Setup of our studyThis section describes the sets of programs, the criteria used for quantifying the results, and the sets of free parameters considered in the evaluation. 3.1.1 Original program sets used: Simple, Hard, Clean, LargeWe used four different kinds of programs as the benchmarks in our study. Three were programming exercises from a secondsemester Informatics course, the fourth was from a graduate advanced programming course that introduced Java and the AWT to experienced students. For an overview, see Table 3 and ignore the rightmost two columns for now. ` "Simple": maximize flow. An algorithm for computing
the maximum flow through a directed graph with capacityweighted edges.
The program is based on a reusable GraphSearch class not included in the
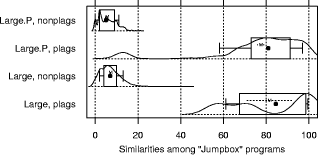
source investigated here. 2To reduce the work required for validation, Wise's algorithm is based on a logarithmic approach to find the longest matching tiles. When JPlag finds a match of length M , JPlag conceptually tries to extend the matching tile token by token until a difference is found. Since Wise uses a smaller M (3 instead of 9), this iterative process in general would take too long. Hence, Wise starts by looking at larger candidates for a match (substring length s = |A|/2 in substep 1 above) and then decreases s in each iteration until s reaches M. Page 1023 Table 3: Characteristics of the program sets and results when using default parameters: Name; number n of programs in set; corresponding number of program pairs; number of plagiarisms (excluding the original base program of each plagiarism cluster); number of pairs that are plagiarism pairs; plagiarism content; precision; recall. See Section 3.1.3 for definitions. "Hard": multiply permutations. Multiply two permutations
represented as permutation matrices which are implemented by an array of
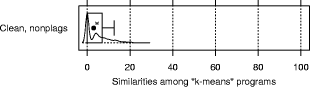
integers indicating the position of the 1 for each row. "Clean": kmeans. The onedimensional kmeans
clustering procedure, using absolute distance as the distance function
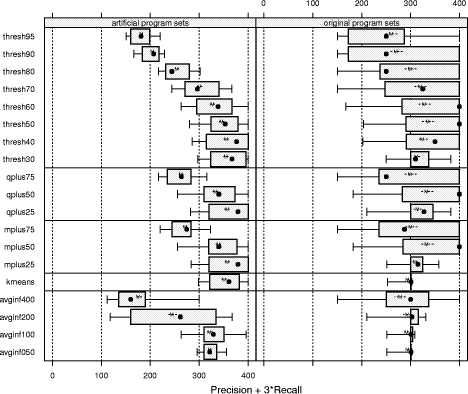
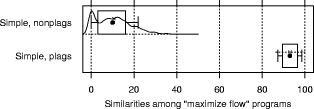
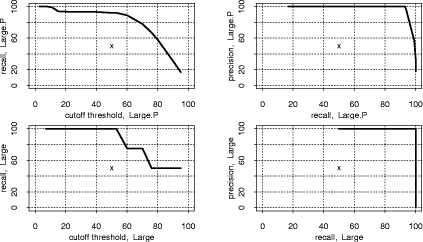
and initializing with equidistant means over the range of the data. "Large": Jumpbox. A simple graphical game where the player has to move the mouse into a square that jumps around on the screen. This set has the longest programs on average and also the largest variation in program design; average program length is 263 LOC. In the program set there are 4 plagiarism pairs. It also contains two other pairs that have a lot of similarity, but that we do not consider to be actual plagiarisms. For one of these, the two programmers have apparently worked together in an early phase, but then finished their programs independently. For the other, the two programs share a common fraction used as a base and taken from an earlier AWT programming exercise. 3.1.2 Artificial program sets: Hard.P, Large.P and othersIn order to investigate the behavior of JPlag more closely, the amount of actual plagiarisms in our program sets is insufficient. Therefore, we collected further plagiarisms by publicly posting a "Call for plagiarisms" on a web site and collecting submissions via email. The students and other programmers who answered our call downloaded a source program from our web page, modified it, and sent it back. They were told to behave like a student who was plagiarizing and trying to deceive a plagiarism detection program, in particular not to spend an inordinate amount of time. The middle 80% of the plagiarists ended up using between 7 and 40 minutes selfreported time. Page 1024 For each of the 12 original programs posted (6 chosen randomly from pro gram set Hard and another 6 from Large), we thus collected up to 14 plagiarized versions, resulting in up to 105 additional plagiarism pairs. Based on these additional plagiarisms, we formed additional program sets for the evaluation of JPlag (see again Table 3): Hard.all is based on the union of Hard and the set of additional plagiarisms collected for it. Hard.P is based on Hard.all but contains only all those programs for which a plagiarism exists as well (original or collected). In this program set, a large fraction of all program pairs is a plagiarism pair. Large.all and Large.P are created in the same manner based on Large and the additional plagiarisms collected for it. Note that for brevity Hard.all and Large.all will not be discussed separately in Sections 3.2 and 3.3 but are included in the results shown in Sections 3.4 and 3.5, where we also used two smaller subsets with high plagiarism content from Hard.all and two more from Large.all. 3.1.3 Evaluation criteria, DefinitionsJPlag can be viewed as an information retrieval system with a fixed query: Given a set of program pairs, retrieve all those pairs that are plagiarisms, but none of the others. For such an operating mode we just need to turn the similarity value produced for each pair into a yes/no decision by applying a cutoff threshold: all pairs with similarity above the threshold will be considered plagiarism pairs. For characterizing the correctness of JPlag's output, we can then use the common information retrieval quality measures "precision" (P) and "recall" (R). These measures are defined as follows. Assume that we have a set of n programs with p = n · (n - 1)/2 pairs and g of these pairs are plagiarism pairs, i.e., one program was plagiarized from the other or both were (directly or indirectly) plagiarized from some common ancestor that is also part of the program set. Now assume that JPlag returns f pairs of programs flagged as plagiarism pairs. If t of these pairs are really true plagiarism pairs and the other f - t are not, then we define precision and recall as P:= 100 · t/f and R:= 100 · t/g, that is, precision is the percentage of flagged pairs that are actual plagiarism pairs and recall is the percentage of all plagiarism pairs that are actually flagged. Furthermore, we define 100 · g/p as the plagiarism content , i.e., the fraction of all pairs that are plagiarism pairs (see the ``%'' column of Table 3). 3.1.4 Other parameters varied in the studyAs described in Section 2.2, there are two free parameters in the JPlag algorithm: the mimimum match length M and the token set used. Both of these were varied in our study as well. The default token set "normal" contains tokens describing major program structure (variable declaration, begin/end of class/method etc.) and control flow (return, break, continue, throw, begin/end of if, while, for etc.), plus 2 tokens for assignments (assign) and method calls (apply). It ignores all structure within expressions (operators, operands) and the identity of methods etc. Besides the default token set, we also used a fairly minimal token set (called "struc") containing only tokens related to control flow and program block structure (but not variable declarations). Further, we used a maximal token set (called "full") containing all possible tokens. Page 1025 We used minimum match lengths 3, 4, 5, 7, 9, 11, 14, 17, 20, 25, 30, and 40. 9 is the default. 3.2 Basic resultsFor summarizing JPlag's performance in a nutshell, we will first report the values of precision and recall for each of our datasets when using the standard parameters (minimum match length 9, normal token set) and a cutoff threshold of 50%. The summary is shown in the rightmost two columns of Table 3. As we see, JPlag's performance is flawless for Simple, Clean, and Large; for three out of our four realworld datasets we do not only obtain all of the plagiarism pairs without exception, but the output is also entirely free of nonplagiarism pairs. For the diffcult dataset Hard we miss 2 of the 6 plagiarism pairs (R = 0.67) and falsely retrieve 7 nonplagiarism pairs in addition to the 4 correct ones. The imperfect recall can of course be improved by decreasing the cutoff threshold, but this will also result in further incorrect outputs. This tradeoff will be analyzed in Section 3.3. The results for the artificial datasets with their high density of plagiarisms are also very good: JPlag detects 92% of all plagiarism pairs in two of the cases (Large.P and Large.all) and 73% in the other two (Hard.P and Hard.all) and except for one case (Hard.all) the results are completely free of spurious outputs. Given the broad range of camouflaging attempts tried by our program au thors described in Section 4, these are rather impressive results. 3.3 Distribution of similarity values; precision/recall tradeoffIdeally, JPlag would report a similarity of 0% for any nonplagiarism pair and of 100% for any plagiarism pair. Practically, however, the distinction is hardly ever so clear. Hence, for judging the robustness of the results shown previously, we will now review the distribution of similarity values that JPlag produced for plagiarism pairs and compare it to the distribution from the nonplagiarism pairs. If the two distributions overlap, one or more program pairs will be judged incorrectly. Simple: "maximize flow" program. Our first example is the program set Simple. The results are shown in Figure 2. This program set leads to a total of 378 program pairs, only 2 of which are actual plagiarism pairs. The top part of the figure shows the similarity value distribution of the 376 nonplagiarism pairs, the bottom part of the 2 plagiarism pairs. JPlag perfectly discriminates the plagiarisms from the other programs for a fairly wide range of cutoff thresholds. The left part of Figure 3 shows how recall changes when we gradually increase the cutoff threshold: only for rather high cutoff thresholds will we miss any plagiarisms. The resulting tradeoff between precision and recall is shown in the right part of the figure. We will always have at least either perfect precision or perfect recall and for appropriately chosen cutoff thresholds we even get both at the same time, i.e., the curve reaches the top right corner of the plot (100/100, the ideal point). Summing up, JPlag's behavior is perfect for this program set. Page 1026 Hard: "multiply permutations" program. Remember that the simplicity of the algorithm suggests a somewhat canonical program structure. We can therefore expect that this program will be an extremely difficult test for JPlag. Figure 4 indeed indicates that the behavior for the Hard program sets is less ideal: There is quite a bit of overlap of the similarity value distributions. Let us consider Hard first and note that in absolute numbers, the plagiarism pair distribution is almost negligible because the plagiarism content is only 0.3%. Despite the difficulty, the distribution of similarity values for the nonplagiarisms is almost the same as for Simple. On the other hand, with one exception the 6 plagiarism pairs in Hard show only moderate similarity, even for a human observer. Looking at the source programs, we got the impression that the students worked at most partially together, but in any case probably finished their programs independently. However, given the small size of the programs, it is impossible to be sure. So one could just as well say these are not plagiarisms at all. But to get a sort of worst case analysis, let us assume the 6 pairs are indeed all real plagiarisms. Then the precision/recall tradeoff is far from ideal (see Figure 5 bottom), but medium cutoff thresholds still lead to a reasonable compromise with a recall of for instance 67 as seen before. For the plagiarismsonly program set Hard.P, the plagiarism pair similarity distribution becomes even wider, as we see in Figure 4 (top), but its median M M Simple, plags Simple, nonplags 0 20 40 60 80 100 Similarities among "maximize flow" programs is at a promising 76% similarity. Figure 2: Distribution of similarity values found among plagiarism pairs and among nonplagiarism pairs of the Simple program set. (The box and whiskers indicate the 10%, 25%, 75%, and 90% quantiles. The fat dot is the median. The `M' and dashed lines indicate the mean plus/minus one standard error. The curved line is a kernel estimation of the probability density function.) JPlag will achieve perfect separation with any cutoff threshold between 47 and 85, i.e. both precision and recall are 100 in this case. Figure 3: Left: recall/threshold tradeoff for Simple. (The `x' marks the middle of the diagram.) This dataset can stand very high cutoff thresholds before recall begins to decline. Right: precision/recall tradeoff for Simple. The behavior is ideal. Page 1027 Figure 4: Distribution of similarity values found among plagiarism pairs and among nonplagiarism pairs, for artificial program set Hard.P (top) and original program set Hard (bottom). For the original programs, there is only little overlap of the similarity ranges. The plagiarism pairs of the artificial programs have a rather wide distribution and hence more overlap with the nonplagiarism's similarities. Figure 5: Left graphs: recall/threshold tradeoff. Right graphs: precision/recall tradeoff. Bottom graphs: Hard. Recall rapidly declines with large thresholds, but at threshold 50 we get a reasonable R = 67. With high recall values, only somewhat unsatisfying precision can be achieved. Top graphs: Hard.P. Recall declines only slowly and steadily for larger cutoff thresholds. A recall R > 80 can be realized with nearperfect precision; a rather good behavior. And indeed, the recall curve and the precision/recall tradeff show a rather benign and satisfying behavior (Figure 5 top): if the threshold is chosen too low, precision drops sharply, but a recall of 70 to 80 can easily be realized with perfect precision. Summing up, JPlag shows good performance (possibly even very good or perfect performance, we don't know) even for this extremely difficult benchmark. Figure 6: Distribution of similarity values found among all pairs in Clean. This program set does not contain any plagiarisms at all and all program pairs have rather low similarity values. The maximum is 27. Figure 7: Distribution of similarity values found among plagiarism pairs and among nonplagiarism pairs, both for Large (bottom half of figure) and Large.P (top half of figure). For the original programs, JPlag achieves perfect separation of plagiarisms and nonplagiarisms with any cutoff threshold between 44 and 56. For the plagiarized programs, there is a single program that is very dissimilar to all others in its plagiarism group, resulting in 14 similarity values in the range 8 to 16, but all others can be separated perfectly by cutoff thresholds between 22 and 43. Clean: "kmeans" program. In this benchmark, there is nothing to find, since the program set does not contain any plagiarisms. As we see, the similarity values found by JPlag are indeed all so small that we will obtain perfect performance with almost any cutoff criterion; see Figure 6. Large: "Jumpbox" program. As can be seen in Figure 7, the separation is very good for the large benchmark as well. For the original program set, perfect performance can be achieved (Figure 8 bottom). For the collected plagiarisms, only a single wellcamouflaged program spoils the otherwise perfect result (Figure 8 top). The deterioration behavior of the recall curve is fairly good in either case. Page 1029 3.4 Influence of token set and minimum match lengthAll of the data presented so far used JPlag's default parameters: The "normal" token set and the standard minimum match length of 9. However, we are also interested how robust JPlag is against changes in these parameters, and how such changes interact with the program set to be analyzed. Therefore, with the performance measure introduced below we will investigate how JPlag's performance changes for different minimum match lengths, cutoff thresholds, token sets, and program sets. We measure the total plagiarism discrimination performance of JPlag by a weighted sum of precision and recall. We choose a relative weight of 3 for recall (versus precision) since it makes sense to penalize false negatives (nondetected plagiarisms) far more than false positives, which merely introduce more work for the final judgement by the human user. Hence, the performance measure becomes P + 3R. The exact value 3 is not important, the results with a weight of 2 or 4 would be similar. We will leave out the voluminous details of the analysis here and only present the results; more detail can be found in [Prechelt et al., 2000]. When analyzing the correlation between the minimum match length M and the P + 3R measure when using the "normal" token set and cutoff threshold 50, we made the following observations:
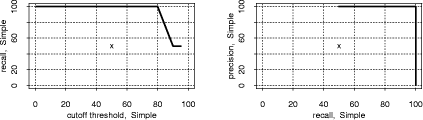
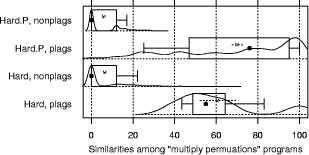
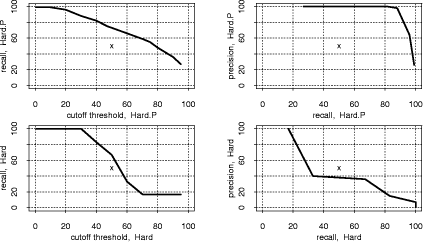
Figure 8: Left: recall/threshold tradeoff. Right: precision/recall tradeoff. Top: Large.P. Bottom: Large. Page 1030 We conclude that JPlag is robust against modestly nonoptimal choice of M. The same analysis using the small "struc" token set finds that due to the shorter token strings, larger values of M are less advisable. Otherwise, the results are remarkably similar to that for the default token set. Finally, for the largest possible token set, called "full", we find that due to the longer token strings, a larger M can more often be tolerated, but modest values still tend to be superior. Otherwise, the results are again similar to both the default and the reduced token set. We conclude that JPlag is highly robust against different choices of token set. This is useful, because it suggests that JPlag may work similarly well for many other programming languages, too, if they allow for a similarly structured token set. Furthermore, we conclude that the default token set and the default minimum match length of 9 are reasonable and robust parameter choices for JPlag for a wide variety of program sets. 3.5 Influence of cutoff criteriaNormally, one will look at the most similar pairs of programs found by JPlag and decide for each pair individually whether it is a plagiarism pair or not. One will progress in this manner towards lower similarity values until one is satisfied that all plagiarisms were found. In some cases, though, a fully automatic decision based on a similarity threshold value is preferable: pairs with this or higher similarity will be considered plagiarisms, while pairs with lower similarity will be considered independent. We call such a criterion a cutoff criterion. A cutoff criterion receives as input a vector s of similarity values and it computes a cutoff threshold T as described above. For evaluating JPlag in fully automatic mode, we have used a number of diffeerent such cutoff criteria. Most of them are adaptive to the similarity distribution of the program set under investigation. From the above discussion we already know that cutoff thresholds in the range 30 to 60 will usually yield the best results. However, it is not clear whether any fixed threshold exists that will almost always be optimal. An adaptive criterion that takes the current similarity distribution into account might be more successful. These are the cutoff criteria that we explored: thresh. The thresT family of cutoff criteria uses the simplest possible method: it does not look at the input vector s at all, but rather applies a fixed cutoff threshold to make the decision. We have used various thresholds T from 30 to 95 percent, resulting in the criteria thresh30 through thresh95. mplus. The mplusD family of cutoffcriteria is somewhat adaptive towards systematically higher or lower similarity values in s. It returns the median (50% quantile, q50) of the similarity values in the vector plus D percent of the distance from the median to 100: T= q50 (s) +D/100#(100-q50 (s)). In contrast to fixed thresholds, these criteria can somewhat adapt to different "base similarities"; they assume that the median similarity represents a typical nonplagiarism pair, because much less than half of all pairs will be plagiarism pairs. We have used mplus25, mplus50, and mplus75. Page 1031 qplus. The qplusD family is equivalent to the mplusD family,
except that the starting point of the offset is the third quartile: T
= q75 (s)+D/100 kmeans. The kmeans cutoff criterion uses onedimensional kmeans clustering to partition the vector into two classes. The class with the higher similarity values will be considered the plagiarism pairs. avginf. The avginfP family of cutoff criteria considers the information
content of pairs with about the same similarity value. The idea here is
that plagiarisms should be rare and hence the range of similarity values
that indicate plagiarisms must have high information content (in the informationtheoretical
sense of the word). Therefore, we select the threshold T as the minimum
threshold for which the average information content Figure 9 compares the performance distribution of the cutoff criteria, based on the performance measure P + 3R. For the original program sets, the best criteria are thresh50, thresh60, qplus50, and mplus50. They all have a median of 400 for P+3R (i.e. at least half of all results are perfect), a mean of about 330 and a first quartile around 280. For the artificial program sets, no criterion manages to be as good as that. The best ones are thresh40, qplus25, and mplus25. This is good news: for practical purposes (where the amount of plagiarisms is usually small), a rule as simple as thresh50 appears to yield about the best possible results. 3.6 Comparison of JPlag and MOSSWe have also run our benchmark program sets through MOSS [Aiken, 1998], postprocessed the results to use the same similarity measure as JPlag and then computed precision and recall for various cutoff thresholds. The results are shown in Table 4. The left part of the table assumes an idealized cutoff criterion that picks the optimal threshold in each case. Note that MOSS generally returns similarity values that are quite a bit lower than those of JPlag. As we see, MOSS's performance is essentially the same as JPlag's as far as Simple, Clean, and Large (or its variants) are concerned. The only difference is that MOSS has to rely on the variability of the cutoff threshold a little more strongly than JPlag. For the variants of the Hard program set, however, JPlag is clearly superior: For Hard.P and Hard.all, JPlag achieves the same recall with much better precision. Note that for Hard.all, JPlag achieves P = 46, R = 88 when t = 30, but this has a lower P + 3R. Moreover, for the original program set Hard, MOSS is unable to find more than one third of the plagiarism pairs, even when the lowest cutoff threshold 10 is being used. Page 1032 A similar situation arises when we choose a fixed threshold for each of the systems, as shown in the right part of the table: We cut off at 50 percent similarity for JPlag and at 30 percent for MOSS. These thresholds are reasonable and tend to balance precision and recall about evenly. The results show that there is no single case where JPlag's precision or recall are worse than that of MOSS, but quite a few where MOSS's are clearly worse than JPlag's - in particular, again, for the Hard program set. As mentioned before, no written description of MOSS's algorithm is available. Therefore, we cannot explain the results. 3.7 Runtime effciencyThe runtime of JPlag increases quadratically with the number of programs in the program set, and slightly superlinearly with the size of the programs. However, the resulting runtimes are usually small. The largest of our program sets, Large.all, contains 99 programs averaging about 250 LOC. The total run time of JPlag for reading and parsing these programs and performing all of the pairwise comparisons, is about 6 seconds wall clock time on a Pentium III machine with 700 MHz using JDK 1.3.1 Hotspot. Of this time, about 4 seconds are spent for parsing the programs and only 2 seconds for the actual comparison. Figure 9: Performance of various cutoff criteria for the artificial program sets (left) or the original program sets (right), using minimum match lengths of 7, 9, or 11, and any of the token sets. Page 1033 Table 4: Comparison of performance of JPlag and MOSS. t: cutoff threshold (for JPlag one of 30, 40, 50, 60, 70, 80, 90; for MOSS one of 10, 20, 30, 40, 50, 60, 70, 80, 90). P: precision. R: recall. Optimal cutoff threshold: threshold is chosen ex post such as to maximize P + 3R. Fixed cutoff threshold: threshold is chosen in advance and is the same for all datasets (for JPlag, this is the situation shown in Table 3). 4 Successful and nonsuccessful plagiarizing attacksThis section analyzes the disguising techniques and the types of attacks we have seen in the programs used for the evaluation. Any single instance of an attack will at most result in what we call a local confusion of JPlag. Consider the shortest segment of the original code that is necessary to apply a disguising technique. If JPlag does not determine any similarity between the original code segment and the result of the attack, we say that JPlag is locally confused. Local confusion critically depends on both the token set used and the minimal match length. For example, a local confusion can be caused if a single line of code (or a single token) is inserted into a code segment of minimal match length. After the insertion, JPlag will usually no longer find corresponding code segments that have enough tokens to match. For another example, if a code segment of minimal match length is split into two parts that are then swapped, JPlag is deceived, too. Unless a program is very short, a number of local confusions is required before a plagiarism escapes its detection (depending on the cutoff criterion). A perfect attack will need to achieve local confusion in every single segment of the original code with minimal match length. JPlag will be successful unless a plagiarist is both creative enough to find enough disguising techniques that can be applied all over the given program (most techniques are only applicable in certain situations) and then eager enough to apply them sufficiently often. 4.1 Futile attacksThe attacks discussed in this section do not work at all, because they do not cause any modification in the list of tokens that are generated and considered by JPlag. Almost every plagiarist has used at least one of these futile disguising techniques. Page 1034
As we see from this list, JPlag's complete ignorance of formatting, comments, literals, and names is paramount to its success. The coarse granularity chosen for the default token set (e.g. ignoring modifiers) is also useful. 4.2 Granularitysensitive attacksRoughly speaking, Java classes consist of declarations of methods and variables. The ordering of declarations is irrelevant. Therefore, a promising line of attack is to reorder the declarations in the implementation. However, if the reordered code segments are longer than the minimal match length, JPlag signals block moves instead of being locally confused. Thus, the success of such attacks critically depends on the granularity of their application. This type of reordering has been used quite frequently by the plagiarists [55 times]. However, only about 15% of them actually confused JPlag.
4.3 Locally confusing attacksThe following types of attacks are usually locally successful, at least with the default token set. Out of 134 times these attacks were applied, only 12 were unsuccessful. However, only very few plagiarists achieved so much local confusion all over a given program as to escape detection.
3Meaning that across all plagiarisms in our study we have seen this attack 48 times overall. Page 1035
Page 1036 The last three types of attacks in this list are the really clever ones that are hard to detect even for a human reader: Modify data structures, add or remove redundancy, or redesign code structure. 5 Summary and conclusionsOur empirical evaluation of JPlag using 4 real sets of Java programs and several further Java program sets containing additional plagiarisms can be summarized as follows:
We do not know exactly to what degree these results transfer to other situations. They might apply to a lesser degree for C and C++, because these languages are currently not parsed but just scanned by JPlag. They might also be weaker for differently structured (or much larger) programs if those make some of the attacks more effective or for different plagiators if those use still different attacks. However, on the whole we would be surprised if the effectiveness of JPlag was ever much lower than demonstrated. It appears that the tokenbased stringsimilarity approach is highly effective for finding plagiarisms, at least if the token strings ignore enough detail. JPlag is an easytouse implementation of this approach for programs written in Java, C, C++, and Scheme. Page 1037 In principle, JPlag can be used for other purposes as well. If a software com pany suspects that a competitor has stolen parts of its source code, then after a court order or agreement of the parties JPlag can compare the two large program systems in question and point out similar regions. JPlag has already been used in such a situation (whose parties wish to remain anonymous) successfully. By pointing out the regions that are different, rather than those that are similar, JPlag can function as a program differencing engine (like Unix diff). Compared to a characterbased difference, a JPlag difference ignores much detail and hence produces much smaller (though also less precise) differences, which may be useful in some situations. References[Aiken, 1998] Alex Aiken. MOSS (Measure Of Software Similarity) plagiarism detection system. http://www.cs.berkeley.edu/?moss/ (as of April 2000) and personal communication, 1998. University of Berkeley, CA. [Berghel and Sallach, 1984] H. L. Berghel and D. L. Sallach. Measurements of program similarity in identical task environments. ACM SIGPLAN Notices, 19(8):65-76, August 1984. [Cluwin et al., 2001] Fintan Cluwin, Anna MacLeod, and Thomas Lancaster. Source code plagiarism in UK HE computing schools: Issues, attitudes and tools. Technical Report SBUCISM0102, School of Computing, South Bank University, London, September 2001. [Donaldson et al., 1981] John L. Donaldson, AnnMarie Lancaster, and Paul H. Sposato. A plagiarism detection system. ACM SIGSCE Bulletin (Proc. of 12th SIGSCE Technical Symp.), 13(1):21--25, February 1981. [Faidhi and Robinson, 1987] J. A. W. Faidhi and S. K. Robinson. An empirical approach for detecting program similarity within a university programming environment. Computers and Education, 11(1):11-19, 1987. [Grier, 1981] Sam Grier. A tool that detects plagiarism in Pascal programs. ACM SIGSCE Bulletin (Proc. of 12th SIGSCE Technical Symp.), 13(1):15-20, February 1981. [Jankowitz, 1988] H. T. Jankowitz. Detecting plagiarism in student Pascal programs. The Computer Journal, 31(1):1-8, 1988. [Karp and Rabin, 1987] R. M. Karp and M. O. Rabin. Efficient randomized patternmatching algorithms. IBM J. of Research and Development, 31(2):249-260, March 1987. [Ottenstein, 1976] Karl J. Ottenstein. An algorithmic approach to the detection and prevention of plagiarism. ACM SIGSCE Bulletin, 8(4):30-41, 1976. [Prechelt et al., 2000] Lutz Prechelt, Guido Malpohl, and Michael Philippsen. JPlag: Finding plagiarisms among a set of programs. Technical Report 20001, Fakultät für Informatik, Universität Karlsruhe, Germany, March 2000. ftp.ira.uka.de. [Verco and Wise, 1996] K. K. Verco and M. J. Wise. Software for detecting suspected plagiarism: Comparing structure and attributecounting systems. In John Rosenberg, editor, Proc. of 1st Australian Conference on Computer Science Education, Sydney, July 1996. ACM. [Whale, 1990] G. Whale. Identification of program similarity in large populations. The Computer Journal, 33(2):140-146, 1990. [Wise, 1992] Michael J. Wise. Detection of similarities in student programs: YAP'ing may be preferable to Plague'ing. ACM SIGSCE Bulletin (Proc. of 23rd SIGCSE Technical Symp.), 24(1):268-271, March 1992. [Wise, 1993] Michael J. Wise. String similarity via greedy string tiling and running KarpRabin matching. ftp://ftp.cs.su.oz.au/michaelw/doc/RKR_GST.ps, Dept. of CS, University of Sydney, December 1993. Page 1038 |
||||||||||||||||||||||||||||||||||||||||||||||||||

 match(a, b, j);
match(a, b, j);  matches {
matches {  match(a, b, maxmatch);
match(a, b, maxmatch);  length.
length.  ((|A|
+ |B|)3 ) if only a single shortest conceivable match
is marked in each iteration, yet all tokens of both strings are covered
in the end [
((|A|
+ |B|)3 ) if only a single shortest conceivable match
is marked in each iteration, yet all tokens of both strings are covered
in the end [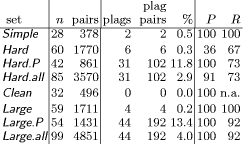
 (100-q75
(s)). The idea is that q75 may represent a larger
case of accidental similarity, so that even small values of D should
not result in false positives. We have used qplus25, qplus50, and qplus75.
(100-q75
(s)). The idea is that q75 may represent a larger
case of accidental similarity, so that even small values of D should
not result in false positives. We have used qplus25, qplus50, and qplus75.
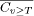 of pairs with this or higher similarity is at least P percent above the
overall average
of pairs with this or higher similarity is at least P percent above the
overall average 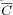 .
To do this, the avginf criteria group similarity values into overlapping
classes of width 5 percent: Given the vector s of similarity values for
all pairs, let Sv be the set of similarity values from
s that have values v . . . v + 5. Then the information
content of each such pair is Cv := - log2
(|Sv|/|s|) and empty classes are defined to have
no information content, i.e., Cv := 0 if Sv
=
.
To do this, the avginf criteria group similarity values into overlapping
classes of width 5 percent: Given the vector s of similarity values for
all pairs, let Sv be the set of similarity values from
s that have values v . . . v + 5. Then the information
content of each such pair is Cv := - log2
(|Sv|/|s|) and empty classes are defined to have
no information content, i.e., Cv := 0 if Sv
= 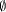 .
Based on these values Cv, the threshold can be determined.
We have used avginf050, avginf100, avginf200, and avginf400.
.
Based on these values Cv, the threshold can be determined.
We have used avginf050, avginf100, avginf200, and avginf400.