|
Verification of Parameterized Protocols
Kai Baukus (Institute of Computer Science and Applied Mathematics CAU Kiel, Germany)
Yassine Lakhnech (VERIMAG, Centre Equation, France)
Karsten Stahl (Institute of Computer Science and Applied Mathematics CAU Kiel, Germany)
Abstract: Recently there has been much interest in the automatic and semi-automatic verification of parameterized networks, i.e., verification of a family of systems 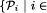 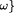 , where each , where each 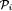 is a network consisting of i processes. is a network consisting of i processes. In this paper, we present a method for the verification of so-called universal properties of fair parameterized networks of similar processes, that is, properties of the form 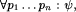 where where 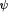 is a quantifier-free LTL formula and the pi refer to processes. To prove an universal property of a parameterized network, we first model the infinite family of networks by a single fair WS1S transition system, that is, a transition system whose variables are set (2nd-order) variables and whose transitions are described in WS1S. Then, we abstract the WS1S system into a finite state system that can be model-checked. We present a generic abstraction relation for verifying universal properties as well as an algorithm for computing an abstract system. is a quantifier-free LTL formula and the pi refer to processes. To prove an universal property of a parameterized network, we first model the infinite family of networks by a single fair WS1S transition system, that is, a transition system whose variables are set (2nd-order) variables and whose transitions are described in WS1S. Then, we abstract the WS1S system into a finite state system that can be model-checked. We present a generic abstraction relation for verifying universal properties as well as an algorithm for computing an abstract system. However, the abstract system may contain infinite computations that have no corresponding fair computations at the concrete level, and hence, in case the property of interest is a progress property, verification may fail because of this. Therefore, we present methods that allow to synthesize fairness conditions from the parameterized network and discuss under which conditions and how to lift fairness conditions of this network to fairness conditions on the abstract system. We implemented our methods in a tool, called PAX, and applied it to several examples.
Keywords: WS1S, abstraction, model checking, parameterized systems, verification
Categories: F.3.1
|