| Submission Procedure |
The Limits of MathematicsG. J. Chaitin
IBM Research Division, P. O. Box 704, Yorktown Heights, NY 10598,
1 Introduction
In a remarkable development, I have constructed a new definition for a self-delimiting universal Turing machine (UTM) that is easy to program and runs very quickly. This provides a new foundation for algorithmic information theory (AIT), which is the theory of the size in bits of programs for self-delimiting UTM's. Previously, AIT had an abstract mathematical quality. Now it is possible to write down executable programs that embody the constructions in the proofs of theorems. So AIT goes from dealing with remote idealized mythical objects to being a theory about practical down-to-earth gadgets that one can actually play with and use. This new self-delimiting UTM is implemented via software written in a new version of LISP that I invented especially for this purpose. This LISP was designed by writing an interpreter for it in Mathematica that was then translated into C. I have tested this software by running it on IBM RS/6000 workstations with the AIX version of UNIX. Using this new software and the latest theoretical ideas, it is now
possible to give a self-contained "hands on" mini-course presenting
very concretely my latest proofs of my two fundamental
information-theoretic incompleteness theorems. The first of these
theorems states that an N-bit formal axiomatic system cannot enable
one to exhibit any specific object with program-size complexity
greater than N + c. The second of these theorems states that an N-bit
formal axiomatic system cannot enable one to determine more than N + Most people believe that anything that is true is true for a reason. These theorems show that some things are true for no reason at all, i.e., accidentally, or at random. As is shown in this course, the algorithms considered in the proofs of
these two theorems are now easy to program and run, and by looking at
the size in bits of these programs one can actually, for the first
time, determine exact values for the constants c and I used this approach and software in an intensive short course on the limits of mathematics that I gave at the University of Maine in Orono in the summer of 1994. I also lectured on this material during a stay at the Santa Fe Institute in the spring of 1995, and at a meeting at the Black Sea University in Romania in the summer of 1995. A summary of the approach that I used on these three occasions will appear under the title "A new version of algorithmic information theory" in a *1 C. Calude (ed.). The Finite, the Unbounded and the Infinite, Proceedings of the Summer School "Chaitin Complexity and Applications, Mangalia, Romania, 27 June - 6 July, 1995. Page 270 forthcoming issue of the new magazine Complexity, which has just been launched by the Santa Fe Institute and John Wiley and Sons. A less technical discussion of the basic ideas that are involved "How to run algorithmic information theory on a computer" will also appear in Complexity. After presenting this material at these three different places, it became obvious to me that it is extremely difficult to understand it in its original form. So next time, at the Rovaniemi Institute of Technology in the spring of 1996, I am going to use the new, more understandable software in this report; everything has been redone in an attempt to make it as easy to understand as possible. For their stimulating invitations, I thank Prof. George Markowsky of the University of Maine, Prof. Cristian Calude of the University of Auckland, Prof. John Casti of the Santa Fe Institute, and Prof. Veikko Keränen of the Rovaniemi Institute of Technology. And I am grateful to IBM for supporting my research for almost thirty years, and to my current management chain at the IBM Research Division, Dan Prener, Christos Georgiou, Eric Kronstadt, Jeff Jaffe, and Jim McGroddy. This report includes the LISP runs *.r used to present the information-theoretic incompleteness theorems of algorithmic information theory. This report does not include the software used to produce these LISP runs. To obtain the software for this course via e-mail, please send requests to chaitin@watson.ibm.com. 2 The New Idea
Here is a quick summary of this new LISP, in which atoms can now
either be words or unsigned decimal integers. First of all, comments
are written like this: [comment]. Each LISP primitive function has a
fixed number of arguments. ' is QUOTE, = is EQ, and atom, car, cdr,
cadr, caddr, cons are provided with their usual meaning. We also have
lambda, define, let, if and display and eval. The notation " indicates
that an S-expression with explicit parentheses follows, not what is
usually the case in this LISP, an M-expression, in which the
parentheses for each primitive function are implicit. nil denotes the
empty list (), and the logical truth values are true and false. For
dealing with unsigned decimal integers we have +, -, *, So far this is fairly standard. The new idea is this. We define our standard self-delimiting universal Turing machine as follows. Its program is in binary, and appears on a tape in the following form. First comes a LISP expression, written in ASCII with 8 bits per character, and terminated by an end-of-line character '\n'. The TM reads in this LISP expression, and then evaluates it. As it does this, two new primitive functions read-bit and read-exp with no arguments may be used to read more from the TM tape. Both of these functions explode if the tape is exhausted, killing the computation. read-bit reads a single bit from the tape. read-exp reads in an entire LISP expression, in 8-bit character chunks, until it reaches an end-of-line character '\n'. This is the only way that information on the TM tape may be accessed, which forces it to be used in a self-delimiting fashion. This is because no algorithm can search for the end of the tape and then use the length of the tape as data in the Page 271 computation. If an algorithm attempts to read a bit that is not on the tape, the algorithm aborts. How is information placed on the TM tape in the first place? Well, in the starting environment, the tape is empty and any attempt to read it will give an error message. To place information on the tape, one must use the primitive function try which tries to see if an expression can be evaluated. Consider the three arguments The value The third element of the value In summary, all that one has to do to simulate a self-delimiting universal Turing machine U(p) running on the binary program p is to write
try no-time-limit 'eval read-exp p
This is an M-expression with parentheses omitted from primitive functions. (Recall that all primitive functions have a fixed number of arguments.) With the parentheses supplied, it becomes the S-expression
(try no-time-limit ('(eval(read-exp))) p)
This says that one is to read a complete LISP S-expression from the TM tape p and then evaluate it without any time limit and using whatever is left on the tape p. Some more primitive functions have also been added. The 2-argument
function append denotes list concatenation, and the 1-argument
function bits converts an S-expression into the list of the bits in
its ASCII character string representation. These are used for
constructing the bit strings that are then put on the TM tape using
try's third argument Page 272 functions size and length that respectively give the number of characters in an S-expression, and the number of elements in a list. Note that the functions append, size and length could be programmed rather than included as built-in primitive functions, but it is extremely convenient and much much faster to provide them built in. Finally a new 1-argument identity function debug with the side-effect
of outputting its argument is provided for debugging. Output produced
by debug is invisible to the "official" display and try output
mechanism. debug is needed because try 3 Course Outline
The course begins by explaining with examples my new LISP. See examples.r. Then the theory of LISP program-size complexity is developed a little bit. LISP program-size complexity is extremely simple and concrete. In particular, it is easy to show that it is impossible to prove that a self-contained LISP expression is elegant, i.e., that no smaller expression has the same value. To prove that an N-character LISP expression is elegant requires a formal axiomatic system that itself has at least LISP complexity N - 410. See godel.r. Next we define our standard self-delimiting universal Turing machine U(p) using
cadr try no-time-limit 'eval read-exp p
as explained in the previous chapter. Next we show that
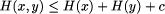 with c = 432: Here
cons eval read-exp
cons eval read-exp
nil
This is an M-expression with parentheses omitted from primitive functions. With all the parentheses supplied, it becomes the S-expression
(cons (eval (read-exp))
(cons (eval (read-exp))
nil))
c = 432 is just 8 bits plus 8 times the size in characters of this LISP S-expression. See utm.r. Page 273 Consider a binary string |x| whose size is x bits. In utm.r we also show that 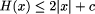 and 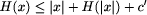 with c = 1106 and Next we turn to the self-delimiting program-size complexity H(X) for
infinite r.e. sets X . This is defined to be the size in bits of the
smallest LISP expression It is in order to deal with such unending expressions Now consider a formal axiomatic system A of complexity N , i.e., with
a set of theorems Next we show two different ways to calculate the halting probability
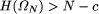 with c = 8000. Again this is done with a program that can actually be run and whose size gives us a value for c. See omega3.r. Consider again the formal axiomatic system A with complexity N , i.e.,
with self-delimiting program-size complexity Last but not least, the philosophical implications of all this should be discussed, especially the extent to which it tends to justify experimental mathematics. This would be along the lines of the discussion in my talk transcript "Randomness in arithmetic and the decline and fall of reductionism in pure mathematics." This concludes our "hands-on" mini-course on the information-theoretic limits of mathematics. Page 274 References
Here is a useful collection of hand-outs for this course: [1] G. J. Chaitin, "Randomness in arithmetic and the decline and fall of reductionism in pure mathematics," in J. Cornwell, Nature's Imagination, Oxford University Press, 1995, pp. 27-44. [2] G. J. Chaitin, "The Berry paradox," Complexity 1 (1995), pp. 26-0. [3] G. J. Chaitin, "A new version of algorithmic information theory," Complexity, to appear. [4] G. J. Chaitin, "How to run algorithmic information theory on a computer," Complexity, to appear. examples.r
LISP Interpreter Run
[ Test new lisp & show how it works ]
aa [ initially all atoms eval to self ]
expression aa
value aa
nil [ except nil = the empty list ]
expression nil
value ()
'aa [ quote = literally ]
expression (' aa)
value aa
'(aa bb cc) [ delimiters are ' " ( ) [ ] blank \n]
expression (' (aa bb cc))
value (aa bb cc)
(aa bb cc) [ what if quote omitted?! ]
expression (aa bb cc)
value aa
'car '(aa bb cc) [ here effect is different ]
expression (' (car (' (aa bb cc))))
value (car (' (aa bb cc)))
car '(aa bb cc) [ car = first element of list ]
expression (car (' (aa bb cc)))
value aa
Page 275
car '((a b)c d)
expression (car (' ((a b) c d)))
value (a b)
car '(aa)
expression (car (' (aa)))
value aa
car aa [ ignore error ]
expression (car aa)
value aa
cdr '(aa bb cc) [ cdr = rest of list ]
expression (cdr (' (aa bb cc)))
value (bb cc)
cdr '((a b)c d)
expression (cdr (' ((a b) c d)))
value (c d)
cdr '(aa)
expression (cdr (' (aa)))
value ()
cdr aa [ ignore error ]
expression (cdr aa)
value aa
cadr '(aa bb cc) [ combinations of car & cdr ]
expression (car (cdr (' (aa bb cc))))
value bb
caddr '(aa bb cc)
expression (car (cdr (cdr (' (aa bb cc)))))
value cc
cons 'aa '(bb cc) [ cons = inverse of car & cdr ]
expression (cons (' aa) (' (bb cc)))
value (aa bb cc)
cons'(a b)'(c d)
expression (cons (' (a b)) (' (c d)))
value ((a b) c d)
Page 276
cons aa nil
expression (cons aa nil)
value (aa)
cons aa ()
expression (cons aa ())
value (aa)
cons aa bb [ ignore error ]
expression (cons aa bb)
value aa
("cons aa) [ supply nil for missing arguments ]
expression (cons aa)
value (aa)
("cons '(aa) '(bb) '(cc)) [ ignore extra arguments ]
expression (cons (' (aa)) (' (bb)) (' (cc)))
value ((aa) bb)
atom ' aa [ is-atomic? predicate ]
expression (atom (' aa))
value true
atom '(aa)
expression (atom (' (aa)))
value false
atom '( )
expression (atom (' ()))
value true
= aa bb [ are-equal-S-expressions? predicate ]
expression (= aa bb)
value false
= aa aa
expression (= aa aa)
value true
= '(a b)'(a b)
expression (= (' (a b)) (' (a b)))
value true
Page 277
= '(a b)'(a x)
expression (= (' (a b)) (' (a x)))
value false
if true x y [ if ... then ... else ... ]
expression (if true x y)
value x
if false x y
expression (if false x y)
value y
if xxx x y [ anything not false is true ]
expression (if xxx x y)
value x
[ display intermediate results ]
cdr display cdr display cdr display '( a b c d e )
expression (cdr (display (cdr (display (cdr (display (' (a b
c d e))))))))
display (a b c d e)
display (b c d e)
display (c d e)
value (d e)
('lambda(x y)x 1 2) [ lambda expression ]
expression ((' (lambda (x y) x)) 1 2)
value 1
('lambda(x y)y 1 2)
expression ((' (lambda (x y) y)) 1 2)
value 2
('lambda(x y)cons y cons x nil 1 2)
expression ((' (lambda (x y) (cons y (cons x nil)))) 1 2)
value (2 1)
(if true "car "cdr '(a b c)) [ function expressions ]
expression ((if true car cdr) (' (a b c)))
value a
(if false "car "cdr '(a b c))
expression ((if false car cdr) (' (a b c)))
value (b c)
Page 278
('lambda()cons x cons y nil) [ function with no arguments ]
expression ((' (lambda () (cons x (cons y nil)))))
value (x y)
[ Here is a way to create an expression and then
evaluate it in the current environment. EVAL (see
below) does this using a clean environment instead. ]
(display
cons "lambda cons nil cons display 'cons x cons y nil nil)
expression ((display (cons lambda (cons nil (cons (display ('
(cons x (cons y nil)))) nil)))))
display (cons x (cons y nil))
display (lambda () (cons x (cons y nil)))
value (x y)
[ let ... be ... in ... ]
let x a cons x cons x nil [ first case, let x be ... in ... ]
expression ((' (lambda (x) (cons x (cons x nil)))) a)
value (a a)
x
expression x
value x
[ second case, let (f x) be ... in ... ]
let (f x) if atom display x x (f car x)
(f '(((a)b)c))
expression ((' (lambda (f) (f (' (((a) b) c))))) (' (lambda (
x) (if (atom (display x)) x (f (car x))))))
display (((a) b) c)
display ((a) b)
display (a)
display a
value a
f
expression f
value f
append '(a b c) '(d e f) [ concatenate-list primitive ]
expression (append (' (a b c)) (' (d e f)))
value (a b c d e f)
[ define "by hand" temporarily ]
Page 279
let (cat x y) if atom x y cons car x (cat cdr x y)
(cat '(a b c) '(d e f))
expression ((' (lambda (cat) (cat (' (a b c)) (' (d e f)))))
(' (lambda (x y) (if (atom x) y (cons (car x) (cat
(cdr x) y))))))
value (a b c d e f)+
cat
expression cat
value cat
[ define "by hand" permanently ]
define (cat x y) if atom x y cons car x (cat cdr x y)
define cat
value (lambda (x y) (if (atom x) y (cons (car x) (cat (c
dr x) y))))
cat
expression cat
value (lambda (x y) (if (atom x) y (cons (car x) (cat (c
dr x) y))))
(cat '(a b c) '(d e f))
expression (cat (' (a b c)) (' (d e f)))
value (a b c d e f)
define x (a b c) [ define atom, not function ]
define x
value (a b c)
cons x nil
expression (cons x nil)
value ((a b c))
define x (d e f)
define x
value (d e f)
cons x nil
expression (cons x nil)
value ((d e f))
size abc [ size of S-expression in characters ]
expression (size abc)
Page 280
value 3
size ' ( a b c )
expression (size (' (a b c)))
value 7
length ' ( a b c ) [ number of elements in list ]
expression (length (' (a b c)))
value 3
length display bits ' a [ S-expression --> bits ]
expression (length (display (bits (' a))))
display (0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0)
value 16
length display bits ' abc [ extra character is \n ]
expression (length (display (bits (' abc))))
display (0 1 1 0 0 0 0 1 0 1 1 0 0 0 1 0 0 1 1 0 0 0 1 1 0
0 0 0 1 0 1 0)
value 32
length display bits nil
expression (length (display (bits nil)))
display (0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0)
value 24
length display bits ' (a)
expression (length (display (bits (' (a)))))
display (0 0 1 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0
0 0 0 1 0 1 0)
value 32
[ plus ]
+ abc 15 [ not number --> 0 ]
expression (+ abc 15)
value 15
+ '(abc) 15
expression (+ (' (abc)) 15)
value 15
+ 10 15
expression (+ 10 15)
value 25
- 10 15 [ non-negative minus ]
Page 281 expression (- 10 15) value 0 - 15 10 expression (- 15 10) value 5 * 10 15 [ times ] expression (* 10 15) value 150 Page 282
expression (>= 10 10)
value true
= 10 15 [ equal ]
expression (= 10 15)
value false
= 10 10
expression (= 10 10)
value true
[ here not number isn't considered zero ]
= abc 0
expression (= abc 0)
value false
= 0003 3 [ other ways numbers are funny ]
expression (= 3 3)
value true
000099 [ leading zeros removed ]
expression 99
value 99
[ and numbers are constants ]
let x b cons x cons x nil
expression ((' (lambda (x) (cons x (cons x nil)))) b)
value (b b)
let 99 45 cons 99 cons 99 nil
expression ((' (lambda (99) (cons 99 (cons 99 nil)))) 45)
value (99 99)
define 99 45
define 99
value 45
cons 99 cons 99 nil
expression (cons 99 (cons 99 nil))
value (99 99)
[ decimal<-->binary conversions ]
base10-to-2 255
Page 283
expression (base10-to-2 255)
value (1 1 1 1 1 1 1 1)
base10-to-2 256
expression (base10-to-2 256)
value (1 0 0 0 0 0 0 0 0)
base10-to-2 257
expression (base10-to-2 257)
value (1 0 0 0 0 0 0 0 1)
base2-to-10 '(1 1 1 1)
expression (base2-to-10 (' (1 1 1 1)))
value 15
base2-to-10 '(1 0 0 0 0)
expression (base2-to-10 (' (1 0 0 0 0)))
value 16
base2-to-10 '(1 0 0 0 1)
expression (base2-to-10 (' (1 0 0 0 1)))
value 17
[ illustrate eval & try ]
eval display '+ display 5 display 15
expression (eval (display (' (+ (display 5) (display 15)))))
display (+ (display 5) (display 15))
display 5
display 15
value 20
try 0 display '+ display 5 display 15 nil
expression (try 0 (display (' (+ (display 5) (display 15))))
nil)
display (+ (display 5) (display 15))
value (success 20 (5 15))
try 0 display '+ debug 5 debug 15 nil
expression (try 0 (display (' (+ (debug 5) (debug 15)))) nil)
display (+ (debug 5) (debug 15))
debug 5
debug 15
value (success 20 ())
[ eval & try use initial variable bindings ]
Page 284
cons x nil
expression (cons x nil)
value ((d e f))
eval 'cons x nil
expression (eval (' (cons x nil)))
value (x)
try 0 'cons x nil nil
expression (try 0 (' (cons x nil)) nil)
value (success (x) ())
define five! [ to illustrate time limits ]
let (f x) if = display x 0 1 * x (f - x 1)
(f 5)
define five!
value ((' (lambda (f) (f 5))) (' (lambda (x) (if (= (dis
play x) 0) 1 (* x (f (- x 1)))))))
eval five!
expression (eval five!)
display 5
display 4
display 3
display 2
display 1
display 0
value 120
[ by the way, numbers can be big: ]
let (f x) if = x 0 1 * x (f - x 1)
(f 100) [ one hundred factorial! ]
expression ((' (lambda (f) (f 100))) (' (lambda (x) (if (= x
0) 1 (* x (f (- x 1)))))))
value 93326215443944152681699238856266700490715968264381
62146859296389521759999322991560894146397615651828
62536979208272237582511852109168640000000000000000
00000000
[ time limit is nesting depth of re-evaluations
due to function calls & eval & try ]
try 0 five! nil
expression (try 0 five! nil)
value (failure out-of-time ())
try 1 five! nil
Page 285
expression (try 1 five! nil)
value (failure out-of-time ())
try 2 five! nil
expression (try 2 five! nil)
value (failure out-of-time (5))
try 3 five! nil
expression (try 3 five! nil)
value (failure out-of-time (5 4))
try 4 five! nil
expression (try 4 five! nil)
value (failure out-of-time (5 4 3))
try 5 five! nil
expression (try 5 five! nil)
value (failure out-of-time (5 4 3 2))
try 6 five! nil
expression (try 6 five! nil)
value (failure out-of-time (5 4 3 2 1))
try 7 five! nil
expression (try 7 five! nil)
value (success 120 (5 4 3 2 1 0))
try no-time-limit five! nil
expression (try no-time-limit five! nil)
value (success 120 (5 4 3 2 1 0))
define two* [ to illustrate running out of data ]
let (f x) if = 0 x nil
cons * 2 display read-bit (f - x 1)
(f 5)
define two*
value ((' (lambda (f) (f 5))) (' (lambda (x) (if (= 0 x)
nil (cons (* 2 (display (read-bit))) (f (- x 1)))
))))
try 6 two* '(1 0 1 0 1)
expression (try 6 two* (' (1 0 1 0 1)))
value (failure out-of-time (1 0 1 0 1))
try 7 two* '(1 0 1 0 1)
Page 286
expression (try 7 two* (' (1 0 1 0 1)))
value (success (2 0 2 0 2) (1 0 1 0 1))
try 7 two* '(1 0 1)
expression (try 7 two* (' (1 0 1)))
value (failure out-of-data (1 0 1))
try no-time-limit two* '(1 0 1)
expression (try no-time-limit two* (' (1 0 1)))
value (failure out-of-data (1 0 1))
try 18
'let (f x) if = 0 x nil
cons * 2 display read-bit (f - x 1)
(f 16)
bits 'a
expression (try 18 (' ((' (lambda (f) (f 16))) (' (lambda (x)
(if (= 0 x) nil (cons (* 2 (display (read-bit)))
(f (- x 1)))))))) (bits (' a)))
value (success (0 2 2 0 0 0 0 2 0 0 0 0 2 0 2 0) (0 1 1
0 0 0 0 1 0 0 0 0 1 0 1 0))
[ illustrate nested try's ]
[ most constraining limit wins ]
try 20
'cons abcdef try 10
'let (f n) (f display + n 1) (f 0) [infinite loop]
nil nil
expression (try 20 (' (cons abcdef (try 10 (' ((' (lambda (f)
(f 0))) (' (lambda (n) (f (display (+ n 1)))))))
nil))) nil)
value (success (abcdef failure out-of-time (1 2 3 4 5 6
7 8 9)) ())
try 10
'cons abcdef try 20
'let (f n) (f display + n 1) (f 0) [infinite loop]
nil nil
expression (try 10 (' (cons abcdef (try 20 (' ((' (lambda (f)
(f 0))) (' (lambda (n) (f (display (+ n 1)))))))
nil))) nil)
value (failure out-of-time ())
try 10
'cons abcdef try 20
'let (f n) (f debug + n 1) (f 0) [infinite loop]
nil nil
expression (try 10 (' (cons abcdef (try 20 (' ((' (lambda (f)
Page 287
(f 0))) (' (lambda (n) (f (debug (+ n 1))))))) ni
l))) nil)
debug 1
debug 2
debug 3
debug 4
debug 5
debug 6
debug 7
debug 8
value (failure out-of-time ())
try no-time-limit
'cons abcdef try 20
'let (f n) (f display + n 1) (f 0) [infinite loop]
nil nil
expression (try no-time-limit (' (cons abcdef (try 20 (' (('
(lambda (f) (f 0))) (' (lambda (n) (f (display (+
n 1))))))) nil))) nil)
value (success (abcdef failure out-of-time (1 2 3 4 5 6
7 8 9 10 11 12 13 14 15 16 17 18 19)) ())
try 10
'cons abcdef try no-time-limit
'let (f n) (f display + n 1) (f 0) [infinite loop]
nil nil
expression (try 10 (' (cons abcdef (try no-time-limit (' (('
(lambda (f) (f 0))) (' (lambda (n) (f (display (+
n 1))))))) nil))) nil)
value (failure out-of-time ())
[ illustrate read-bit & read-exp ]
read-bit
expression (read-bit)
value out-of-data
read-exp
expression (read-exp)
value out-of-data
try 0 'read-bit nil
expression (try 0 (' (read-bit)) nil)
value (failure out-of-data ())
try 0 'read-exp nil
expression (try 0 (' (read-exp)) nil)
value (failure out-of-data ())
Page 288
try 0 'read-exp bits 'abc
expression (try 0 (' (read-exp)) (bits (' abc)))
value (success abc ())
try 0 'read-exp bits '(abc def)
expression (try 0 (' (read-exp)) (bits (' (abc def))))
value (success (abc def) ())
try 0 'read-exp bits '(abc(def ghi)jkl)
expression (try 0 (' (read-exp)) (bits (' (abc (def ghi) jkl)
)))
value (success (abc (def ghi) jkl) ())
try 0 'cons read-exp cons read-bit nil bits 'abc
expression (try 0 (' (cons (read-exp) (cons (read-bit) nil)))
(bits (' abc)))
value (failure out-of-data ())
try 0 'cons read-exp cons read-bit nil append bits 'abc '(0)
expression (try 0 (' (cons (read-exp) (cons (read-bit) nil)))
(append (bits (' abc)) (' (0))))
value (success (abc 0) ())
try 0 'cons read-exp cons read-bit nil append bits 'abc '(1)
expression (try 0 (' (cons (read-exp) (cons (read-bit) nil)))
(append (bits (' abc)) (' (1))))
value (success (abc 1) ())
try 0 'read-exp bits '(a b c)
expression (try 0 (' (read-exp)) (bits (' (a b c))))
value (success (a b c) ())
try 0 'cons read-exp cons read-exp nil bits '(a b c)
expression (try 0 (' (cons (read-exp) (cons (read-exp) nil)))
(bits (' (a b c))))
value (failure out-of-data ())
try 0 'cons read-exp cons read-exp nil
append bits '(a b c) bits '(d e f)
expression (try 0 (' (cons (read-exp) (cons (read-exp) nil)))
(append (bits (' (a b c))) (bits (' (d e f)))))
value (success ((a b c) (d e f)) ())
bits 'a [ to get characters codes ]
expression (bits (' a))
Page 289
value (0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0)
try 0 'read-exp '(0 1 1 0 0 0 0 1) ['a' but no \n character]
expression (try 0 (' (read-exp)) (' (0 1 1 0 0 0 0 1)))
value (failure out-of-data ())
try 0 'read-exp '(0 1 1 0 0 0 0 1 0 0 0 0 1 0 1)[0 missing]
expression (try 0 (' (read-exp)) (' (0 1 1 0 0 0 0 1 0 0 0 0
1 0 1)))
value (failure out-of-data ())
try 0 'read-exp '(0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0) [okay]
expression (try 0 (' (read-exp)) (' (0 1 1 0 0 0 0 1 0 0 0 0
1 0 1 0)))
value (success a ())
[ if we get to \n reading 8 bits at a time,
we will always interpret as a valid S-expression ]
try 0 'read-exp
'(0 0 0 0 1 0 1 0) [nothing in record; only \n]
expression (try 0 (' (read-exp)) (' (0 0 0 0 1 0 1 0)))
value (success () ())
try 0 'read-exp '(1 1 1 1 1 1 1 1 [unprintable character]
0 0 0 0 1 0 1 0) [is deleted]
expression (try 0 (' (read-exp)) (' (1 1 1 1 1 1 1 1 0 0 0 0
1 0 1 0)))
value (success () ())
bits () [ to get characters codes ]
expression (bits ())
value (0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0)
[ three left parentheses==>three right parentheses supplied ]
try 0 'read-exp '(0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0
0 0 1 0 1 0 0 0 0 0 0 0 1 0 1 0)
expression (try 0 (' (read-exp)) (' (0 0 1 0 1 0 0 0 0 0 1 0
1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 1 0)))
value (success ((())) ())
[ right parenthesis 'a'==>left parenthesis supplied ]
try 0 'read-exp '(0 0 1 0 1 0 0 1 0 1 1 0 0 0 0 1
0 0 0 0 1 0 1 0) [ & extra 'a' ignored ]
expression (try 0 (' (read-exp)) (' (0 0 1 0 1 0 0 1 0 1 1 0
0 0 0 1 0 0 0 0 1 0 1 0)))
value (success () ())
Page 290
[ 'a' right parenthesis==>'a' is seen & parenthesis ]
try 0 'read-exp '(0 1 1 0 0 0 0 1 0 0 1 0 1 0 0 1
0 0 0 0 1 0 1 0) [ is ignored ]
expression (try 0 (' (read-exp)) (' (0 1 1 0 0 0 0 1 0 0 1 0
1 0 0 1 0 0 0 0 1 0 1 0)))
value (success a ())
End of LISP Run
Elapsed time is 16 seconds.
godel.r
LISP Interpreter Run
[[[
Show that a formal system of lisp complexity
H_lisp (FAS) = N cannot enable us to exhibit
an elegant S-expression of size greater than N + 410.
An elegant lisp expression is one with the property
that no smaller S-expression has the same value.
Setting: formal axiomatic system is never-ending
lisp expression that displays elegant S-expressions.
]]]
[Here is the key expression.]
define expression
let (examine x)
if atom x false
if < n size car x car x
(examine cdr x)
let fas 'display Page 291
(' (lambda () ((' (lambda (v) ((' (lambda (s) (if
s (eval s) (if (= success (car v)) failure ((' (la
mbda (t) (loop))) (+ t 1)))))) (examine (car (cdr
(cdr v))))))) (try t fas nil))))))) 0))) (+ 410 (s
ize fas))))) (' (display (Page 292
s (eval s) (if (= success (car v)) failure ((' (la
mbda (t) (loop))) (+ t 1)))))) (examine (car (cdr
(cdr v))))))) (try t fas nil))))))) 0))) (+ 410 (s
ize fas))))) (' (display (utm.r
LISP Interpreter Run
[[[
First steps with my new construction for
a self-delimiting universal Turing machine.
We show that
H(x,y) <= H(x) + H(y) + c
and determine c.
Consider a bit string x of length .
We also show that
H(x) <= 2|x| + c
and that
H(x) <= |x| + H(the binary string for |x|) + c
and determine both these c's.
]]]
[
Here is the self-delimiting universal Turing machine!
]
define (U p) cadr try no-time-limit 'eval read-exp p
define U
value (lambda (p) (car (cdr (try no-time-limit (' (eval
(read-exp))) p))))+
(U bits 'cons x cons y cons z nil)
expression (U (bits (' (cons x (cons y (cons z nil))))))
value (x y z)
(U append bits 'cons a debug read-exp
bits '(b c d)
)
expression (U (append (bits (' (cons a (debug (read-exp)))))
(bits (' (b c d)))))
debug (b c d)
value (a b c d)
[
Page 293
The length of alpha in bits is the
constant c in H(x) < + 2|x| + c.
]
define alpha
let (loop) let x read-bit
let y read-bit
if = x y
cons x (loop)
nil
(loop)
define alpha
value ((' (lambda (loop) (loop))) (' (lambda () ((' (lam
bda (x) ((' (lambda (y) (if (= x y) (cons x (loop)
) nil))) (read-bit)))) (read-bit)))))
length bits alpha
expression (length (bits alpha))
value 1104
(U
append
bits alpha
'(0 0 1 1 0 0 1 1 0 1)
)
expression (U (append (bits alpha) (' (0 0 1 1 0 0 1 1 0 1)))
)
value (0 1 0 1)
(U
append
bits alpha
'(0 0 1 1 0 0 1 1 0 0)
)
expression (U (append (bits alpha) (' (0 0 1 1 0 0 1 1 0 0)))
)
value out-of-data
[
The length of beta in bits is the
constant c in H(x,y) <= H(x) + H(y) + c.
]
define beta
cons eval read-exp
cons eval read-exp
nil
define beta
value (cons (eval (read-exp)) (cons (eval (read-exp)) ni
l))
length bits beta
Page 294
expression (length (bits beta))
value 432
(U
append
bits beta
append
bits 'cons a cons b cons c nil
bits 'cons x cons y cons z nil
)
expression (U (append (bits beta) (append (bits (' (cons a (c
ons b (cons c nil))))) (bits (' (cons x (cons y (c
ons z nil))))))))
value ((a b c) (x y z))
(U
append
bits beta
append
append bits alpha '(0 0 1 1 0 0 1 1 0 1)
append bits alpha '(1 1 0 0 1 1 0 0 1 0)
)
expression (U (append (bits beta) (append (append (bits alpha
) (' (0 0 1 1 0 0 1 1 0 1))) (append (bits alpha)
(' (1 1 0 0 1 1 0 0 1 0))))))
value ((0 1 0 1) (1 0 1 0))
[
The length of gamma in bits is the
constant c in H(x) <= |x| + H(|x|) + c
]
define gamma
let (loop k)
if = 0 k nil
cons read-bit (loop - k 1)
(loop base2-to-10 eval read-exp)
define gamma
value ((' (lambda (loop) (loop (base2-to-10 (eval (read-
exp)))))) (' (lambda (k) (if (= 0 k) nil (cons (re
ad-bit) (loop (- k 1)))))))
length bits gamma
expression (length (bits gamma))
value 1024
(U
append
bits gamma
append
[Arbitrary program for U to compute number of bits]
Page 295
bits' '(1 0 0 0)
[That many bits of data]
'(0 0 0 0 0 0 0 1)
)
expression (U (append (bits gamma) (append (bits (' (' (1 0 0
0)))) (' (0 0 0 0 0 0 0 1)))))
value (0 0 0 0 0 0 0 1)
End of LISP Run
Elapsed time is 19 seconds.
godel2.r
LISP Interpreter Run
[[[
Show that a formal system of complexity N
can't prove that a specific object has
complexity > N + 4872.
Formal system is a never halting lisp expression
that output pairs (lisp object, lower bound
on its complexity). E.g., (x 4) means
that x has complexity H(x) greater than or equal to 4.
]]]
[Here is the prefix.]
define pi
let (examine pairs)
if atom pairs false
if < n cadr car pairs
car pairs
(examine cdr pairs)
let t 0
let fas nil
let (loop)
let v try t 'eval read-exp fas
let n + 4872 length fas
let p (examine caddr v)
if p car p
if = car v success failure
if = cadr v out-of-data
let fas append fas cons read-bit nil
(loop)
if = cadr v out-of-time
let t + t 1
(loop)
unexpected-condition
Page 296
(loop)
define pi
value ((' (lambda (examine) ((' (lambda (t) ((' (lambda
(fas) ((' (lambda (loop) (loop))) (' (lambda () ((
' (lambda (v) ((' (lambda (n) ((' (lambda (p) (if
p (car p) (if (= (car v) success) failure (if (= (
car (cdr v)) out-of-data) ((' (lambda (fas) (loop)
)) (append fas (cons (read-bit) nil))) (if (= (car
(cdr v)) out-of-time) ((' (lambda (t) (loop))) (+
t 1)) unexpected-condition)))))) (examine (car (c
dr (cdr v))))))) (+ 4872 (length fas))))) (try t (
' (eval (read-exp))) fas))))))) nil))) 0))) (' (la
mbda (pairs) (if (atom pairs) false (if (! n (car
(cdr (car pairs)))) (car pairs) (examine (cdr pair
s)))))))
[Size pi.]
length bits pi
expression (length (bits pi))
value 4872
[Size pi + fas.]
length
append bits pi
bits 'display '(xyz 9999)
expression (length (append (bits pi) (bits (' (display (' (xy
z 9999)))))))
value 5072
[Here pi finds something suitable.]
cadr try no-time-limit 'eval read-exp
append bits pi
bits 'display '(xyz 5073)
expression (car (cdr (try no-time-limit (' (eval (read-exp)))
(append (bits pi) (bits (' (display (' (xyz 5073)
))))))))
value xyz
[Here pi doesn't find anything suitable.]
cadr try no-time-limit 'eval read-exp
append bits pi
bits 'display '(xyz 5072)
expression (car (cdr (try no-time-limit (' (eval (read-exp)))
(append (bits pi) (bits (' (display (' (xyz 5072)
))))))))
value failure
Page 297 End of LISP Run Elapsed time is 153 seconds. omega.r
LISP Interpreter Run
[[[[ Omega in the limit from below! ]]]]
define (all-bit-strings-of-size k)
if = 0 k '(())
(extend-by-one-bit (all-bit-strings-of-size - k 1))
define all-bit-strings-of-size
value (lambda (k) (if (= 0 k) (' (())) (extend-by-one-bi
t all-bit-strings-of-size (- k 1)))))
define (extend-by-one-bit x)
if atom x nil
cons append car x '(0)
cons append car x '(1)
(extend-by-one-bit cdr x)
define extend-by-one-bit
value (lambda (x) (if (atom x) nil (cons (append (car x)
(' (0))) (cons (append (car x) (' (1))) (extend-b
y-one-bit (cdr x))))))
define (count-halt p)
if atom p 0
+
if = success car try t 'eval read-exp car p
1 0
(count-halt cdr p)
define count-halt
value (lambda (p) (if (atom p) 0 (+ (if (= success (car
(try t(' (eval (read-exp))) (car p)))) 1 0) (coun
t-halt (cdr p)))))
define (omega t) cons (count-halt (all-bit-strings-of-size t))
cons /
cons Page 298 (omega 1) expression (omega 1) value (0 / 2) (omega 2) expression (omega 2) value (0 / 4) (omega 3) expression (omega 3) value (0 / 8) (omega 8) expression (omega 8) value (1 / 256) End of LISP Run Elapsed time is 38 seconds. omega2.r
LISP Interpreter Run
[[[[ Omega in the limit from below! ]]]]
define (count-halt prefix bits-left-to-extend)
if = bits-left-to-extend 0
if = success car try t 'eval read-exp prefix
1 0
+ (count-halt append prefix '(0) - bits-left-to-extend 1)
(count-halt append prefix '(1) - bits-left-to-extend 1)
define count-halt
value (lambda (prefix bits-left-to-extend) (if (= bits-l
eft-to-extend 0) (if (= success (car (try t (' (ev
al (read-exp))) prefix))) 1 0) (+ (count-halt (app
end prefix (' (0))) (- bits-left-to-extend 1)) (co
unt-halt (append prefix (' (1))) (- bits-left-to-e
xtend 1)))))
define (omega t) cons (count-halt nil t)
cons /
cons Page 299 (omega 0) expression (omega 0) value (0 / 1) (omega 1) expression (omega 1) value (0 / 2) (omega 2) expression (omega 2) value (0 / 4) (omega 3) expression (omega 3) value (0 / 8) (omega 8) expression (omega 8) value (1 / 256) End of LISP Run Elapsed time is 33 seconds. omega3.r
LISP Interpreter Run
[[[
Show that
H(Omega_n) > n - 8000.
Omega_n is the first n bits of Omega,
where we choose
Omega = xxx0111111...
instead of
Omega = xxx1000000...
if necessary.
]]]
[Here is the prefix.]
define pi
let (count-halt prefix bits-left-to-extend)
if = bits-left-to-extend 0
if = success car try t 'eval read-exp prefix
1 0
+ (count-halt append prefix '(0) - bits-left-to-extend 1)
Page 300
(count-halt append prefix '(1) - bits-left-to-extend 1)
let (omega t) cons (count-halt nil t)
cons /
cons Page 301
[Run pi.]
cadr try no-time-limit 'eval read-exp
append bits pi
bits '
[Program to compute first n = 8 bits of Omega]
'(0 0 0 0 0 0 0 1)
expression (car (cdr (try no-time-limit (' (eval (read-exp)))
(append (bits pi) (bits (' (' (0 0 0 0 0 0 0 1)))
)))))
value (out-of-data out-of-data out-of-data out-of-data o
ut-of-data out-of-data out-of-data out-of-data out
-of-data out-of-data () out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
Page 302
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data out-of-data out-of-data out-of-data
out-of-data out-of-data out-of-data out-of-data ou
t-of-data out-of-data out-of-data out-of-data out-
of-data out-of-data out-of-data out-of-data out-of
-data out-of-data out-of-data out-of-data out-of-d
ata out-of-data out-of-data out-of-data out-of-dat
a out-of-data)
[Size pi.]
length bits pi
expression (length (bits pi))
value 8000
End of LISP Run
Elapsed time is 148 seconds.
godel3.r
LISP Interpreter Run
[[[
Show that a formal system of complexity N
can't determine more than N + 8000 + 7328
= N + 15328 bits of Omega.
Formal system is a never halting lisp expression
that outputs lists of the form (1 0 X 0 X X X X 1 0).
This stands for the fractional part of Omega,
and means that these 0,1 bits of Omega are known.
X stands for an unknown bit.
]]]
[Here is the prefix.]
define pi
let (number-of-bits-determined w)
if atom w 0
+ (number-of-bits-determined cdr w)
if = X car w
0
1
Page 303
let (supply-missing-bits w)
if atom w nil
cons if = X car w
read-bit
car w
(supply-missing-bits cdr w)
let (examine w)
if atom w false
[if < n (number-of-bits-determined car w)]
[ Change n to 1 here so will succeed. ]
if < 1 (number-of-bits-determined car w)
car w
(examine cdr w)
let t 0
let fas nil
let (loop)
let v try t 'eval read-exp fas
let n + 8000 + 7328 length fas
let w (examine caddr v)
if w (supply-missing-bits w)
if = car v success failure
if = cadr v out-of-data
let fas append fas cons read-bit nil
(loop)
if = cadr v out-of-time
let t + t 1
(loop)
unexpected-condition
(loop)
define pi
value ((' (lambda (number-of-bits-determined) ((' (lambd
a (supply-missing-bits) ((' (lambda (examine) (('
(lambda (t) ((' (lambda (fas) ((' (lambda (loop) (
loop))) (' (lambda () ((' (lambda (v) ((' (lambda
(n) ((' (lambda (w) (if w (supply-missing-bits w)
(if (= (car v) success) failure (if (= (car (cdr v
)) out-of-data) ((' (lambda (fas) (loop))) (append
fas (cons (read-bit) nil))) (if (= (car (cdr v))
out-of-time) ((' (lambda (t) (loop))) (+ t 1)) une
xpected-condition)))))) (examine (car (cdr (cdr v)
)))))) (+ 8000 (+ 7328 (length fas)))))) (try t ('
(eval (read-exp))) fas))))))) nil))) 0))) (' (lam
bda (w) (if (atom w) false (if (! 1 (number-of-bit
s-determined (car w))) (car w) (examine (cdr w))))
))))) (' (lambda (w) (if (atom w) nil (cons (if (=
X (car w)) (read-bit) (car w)) (supply-missing-bi
ts (cdr w))))))))) (' (lambda (w) (if (atom w) 0 (
+ (number-of-bits-determined (cdr w)) (if (= X (ca
r w)) 0 1))))))
Page 304
[Size pi.]
length bits pi
expression (length (bits pi))
value 7328
[Run pi.]
cadr try no-time-limit 'eval read-exp
append bits pi
append [Toy formal system with only one theorem.]
bits 'display '(1 X 0)
[Missing bit of omega that is needed.]
'(1)
expression (car (cdr (try no-time-limit (' (eval (read-exp)))
(append (bits pi) (append (bits (' (display (' (1
X 0))))) (' (1)))))))
value (1 1 0)
End of LISP Run
Elapsed time is 94 seconds.
|
|||||||||||||||||
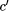 scattered bits of the halting probability
scattered bits of the halting probability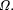
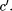
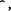 <, >,
<=, >=, base10-to-2, base2-to-10.
<, >,
<=, >=, base10-to-2, base2-to-10.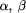 and
and 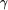 of try. The meaning of the
first argument is as follows. If
of try. The meaning of the
first argument is as follows. If  is no-time-limit, then there is no
depth limit. Otherwise
is no-time-limit, then there is no
depth limit. Otherwise  must be an unsigned decimal integer, and
gives the depth limit (limit on the nesting depth of function calls
and re-evaluations). The second argument
must be an unsigned decimal integer, and
gives the depth limit (limit on the nesting depth of function calls
and re-evaluations). The second argument 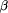 of try is the expression
to be evaluated as long as the depth limit
of try is the expression
to be evaluated as long as the depth limit  is not exceeded. And the
third argument
is not exceeded. And the
third argument 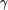 of try is a list of bits to be used as the TM tape.
of try is a list of bits to be used as the TM tape. returned by the
primitive function try is a triple. The first element of
returned by the
primitive function try is a triple. The first element of 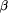 was completed
successfully, and the first element of
was completed
successfully, and the first element of  is failure if this was not the
case. The second element of
is failure if this was not the
case. The second element of  was exceeded. These are the only possible
error flags, because this LISP is designed with maximally permissive
semantics. If the computation
was exceeded. These are the only possible
error flags, because this LISP is designed with maximally permissive
semantics. If the computation  will be a list of N elements. The N arguments of
display appear in
will be a list of N elements. The N arguments of
display appear in  ), but try can also be used to
capture all the output that
), but try can also be used to
capture all the output that 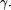 . We also provide the 1-argument
. We also provide the 1-argument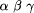 suppresses all output
suppresses all output 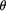 produced within its depth-controlled evaluation of
produced within its depth-controlled evaluation of 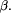 . Instead try
collects all output
. Instead try
collects all output 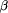 for inclusion in the final value
for inclusion in the final value  that try returns, namely
that try returns, namely 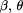 ).
).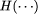 denotes the size in bits of the smallest program that
makes our standard universal Turing machine compute
denotes the size in bits of the smallest program that
makes our standard universal Turing machine compute 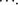 Thus this inequality
states that the information needed to compute the pair (x; y) is bounded by
a constant c plus the sum of the information needed to compute x and the
information needed to compute y. Consider
Thus this inequality
states that the information needed to compute the pair (x; y) is bounded by
a constant c plus the sum of the information needed to compute x and the
information needed to compute y. Consider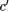 = 1024. As before, the programs for doing this
are exhibited and run.
= 1024. As before, the programs for doing this
are exhibited and run.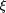 that executes forever without halting and
outputs the members of the r.e. set X using the LISP primitive
display, which is an identity function with the side-effect of
outputting the value of its argument. Note that this LISP expression
that executes forever without halting and
outputs the members of the r.e. set X using the LISP primitive
display, which is an identity function with the side-effect of
outputting the value of its argument. Note that this LISP expression 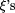 program size.
program size.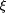 that the LISP
primitive function for time-limited evaluation try captures all output
from display within its second argument
that the LISP
primitive function for time-limited evaluation try captures all output
from display within its second argument 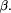
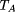 that considered as an r.e. set as above has
self-delimiting program-size complexity
that considered as an r.e. set as above has
self-delimiting program-size complexity 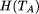 = N . We show that A
cannot enable us to exhibit a specific S-expression s with
self-delimiting complexity H(s) greater than N + c. Here c =
4872. See godel2.r.
= N . We show that A
cannot enable us to exhibit a specific S-expression s with
self-delimiting complexity H(s) greater than N + c. Here c =
4872. See godel2.r.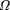 of our standard self-delimiting universal Turing machine in the
limit from below. See omega.r and omega2.r. The first way of doing
this, omega.r, is straight- forward. The second way to calculate
of our standard self-delimiting universal Turing machine in the
limit from below. See omega.r and omega2.r. The first way of doing
this, omega.r, is straight- forward. The second way to calculate 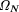 is the first N bits of the
fractional part of the base-two real number
is the first N bits of the
fractional part of the base-two real number 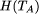 = N . Using the
lower bound of N on
= N . Using the
lower bound of N on 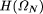 established in omega3.r, we show that A cannot
enable us to determine more than the first
established in omega3.r, we show that A cannot
enable us to determine more than the first 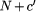 bits of
bits of 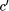 = 15328. In
fact, we show that A cannot enable us to determine more than N +
= 15328. In
fact, we show that A cannot enable us to determine more than N + 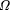 even if they are scattered and we leave gaps. See godel3.r.
even if they are scattered and we leave gaps. See godel3.r. [ power ]
expression
[ power ]
expression 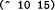 value 1000000000000000
< 10 15 [ less than ]
expression (< 10 15)
value true
< 10 10
expression (< 10 10)
value false
> 15 10 [ greater than ]
expression (> 15 10)
value true
> 10 10
expression (> 10 10)
value false
<= 15 10 [ less than or equal ]
expression ( <= 15 10)
value false
<= 10 10
expression (<= 10 10)
value true
>= 10 15 [ greater than or equal ]
expression (>= 10 15)
value false
>= 10 10
value 1000000000000000
< 10 15 [ less than ]
expression (< 10 15)
value true
< 10 10
expression (< 10 10)
value false
> 15 10 [ greater than ]
expression (> 15 10)
value true
> 10 10
expression (> 10 10)
value false
<= 15 10 [ less than or equal ]
expression ( <= 15 10)
value false
<= 10 10
expression (<= 10 10)
value true
>= 10 15 [ greater than or equal ]
expression (>= 10 15)
value false
>= 10 10
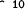 430 [insert FAS here preceeded by ']
let n + 410 size fas
let t 0
let (loop)
let v try t fas nil
let s (examine caddr v)
if s eval s
if = success car v failure
let t + t 1
(loop)
(loop)
define expression
value ((' (lambda (examine) ((' (lambda (fas) ((' (lambd
a (n) ((' (lambda (t) ((' (lambda (loop) (loop)))
430 [insert FAS here preceeded by ']
let n + 410 size fas
let t 0
let (loop)
let v try t fas nil
let s (examine caddr v)
if s eval s
if = success car v failure
let t + t 1
(loop)
(loop)
define expression
value ((' (lambda (examine) ((' (lambda (fas) ((' (lambd
a (n) ((' (lambda (t) ((' (lambda (loop) (loop)))
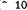 430)))))) (' (lambd
a (x) (if (atom x) false (if (< n (size (car x)))
(car x) (examine (cdr x)))))))
[Size expression.]
size expression
expression (size expression)
value 430
[Run expression & show that it knows its own size
and can find something bigger than it is.]
eval expression
expression (eval expression)
value 10000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
0000000000000000000000000000000
[Here it fails to find anything bigger than it is.]
let (examine x)
if atom x false
if < n size car x car x
(examine cdr x)
let fas 'display
430)))))) (' (lambd
a (x) (if (atom x) false (if (< n (size (car x)))
(car x) (examine (cdr x)))))))
[Size expression.]
size expression
expression (size expression)
value 430
[Run expression & show that it knows its own size
and can find something bigger than it is.]
eval expression
expression (eval expression)
value 10000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
0000000000000000000000000000000
[Here it fails to find anything bigger than it is.]
let (examine x)
if atom x false
if < n size car x car x
(examine cdr x)
let fas 'display 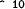 429 [insert FAS here preceeded by ']
let n + 410 size fas
let t 0
let (loop)
let v try t fas nil
let s (examine caddr v)
if s eval s
if = success car v failure
let t + t 1
(loop)
(loop)
expression ((' (lambda (examine) ((' (lambda (fas) ((' (lambd
a (n) ((' (lambda (t) ((' (lambda (loop) (loop)))
(' (lambda () ((' (lambda (v) ((' (lambda (s) (if
429 [insert FAS here preceeded by ']
let n + 410 size fas
let t 0
let (loop)
let v try t fas nil
let s (examine caddr v)
if s eval s
if = success car v failure
let t + t 1
(loop)
(loop)
expression ((' (lambda (examine) ((' (lambda (fas) ((' (lambd
a (n) ((' (lambda (t) ((' (lambda (loop) (loop)))
(' (lambda () ((' (lambda (v) ((' (lambda (s) (if
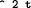 nil
define omega
value (lambda (t) (cons (count-halt (all-bit-strings-of-
size t)) (cons / (cons
nil
define omega
value (lambda (t) (cons (count-halt (all-bit-strings-of-
size t)) (cons / (cons 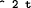 nil
define omega
value (lambda (t) (cons (count-halt nil t) (cons / (cons
(
nil
define omega
value (lambda (t) (cons (count-halt nil t) (cons / (cons
(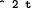 nil
let w eval read-exp
let n length w
let w cons base2-to-10 w
cons /
cons
nil
let w eval read-exp
let n length w
let w cons base2-to-10 w
cons /
cons