| Submission Procedure |
On the Scalability of Molecular Computational Solutions to NP Problems
Abstract: A molecular computational procedure in which
manipulation of DNA strands may be harnessed to solve a classical
problem in NP - the directed Hamiltonian path problem - was recently
proposed [Adleman 1994], [Gifford 1994]. The procedure is in effect a
massively parallel chemical analog computer and has a computational
capacity corresponding to approximately Key Words: Molecular Computation, DNA, NP-problem 1 Introduction
The (directed) Hamiltonian Path Problem (HPP), first proposed by
William Rowan Hamilton, is one of the most troublesome problems in
Graph theory. Very similar to the Euler path problem, it may be stated
as follows: for a graph G with vertices A trial and error approach is theoretically possible but proves impossible in practice for all but the smallest graphs; the number of paths which it is necessary to check simply grows too rapidly. In fact the HPP problem belongs to a class of problems called NP-complete, which rapidly become too complex to be solved by standard (deterministic) computers. Problems of this nature are of considerable importance in computer science. There was therefore considerable interest in a recent report by Adleman which suggested that modern laboratory techniques of molecular biology could be employed to manipulate strands of DNA so as to solve the HPP [Adleman 1994]. A subsequent study has suggested how the method may be adapted for the solution of another classical problem in NP - the "satisfiability" or SAT problem [Lipton 1995]. Page 87 Adleman's insight lay in exploiting the parallelism inherent in chemical systems to yield a massively parallel analog computer, in a brute force approach to solving complex problems in NP. However, while it was noted that chemical systems - and thus molecular computers - can be easily scaled in size, the fundamental question of the scalability of problems solvable by molecular computation was left open. This paper addresses this central issue and, because the discussion draws on the diverse disciplines of molecular biology and computer science, begins with a brief review of both problem classification and Adleman's experiment. 1.1 Classification of Problem Complexity
Time complexity functions describe how the cost of solving a problem grows on increasing the size (or input length), n, of the problem. Computer scientists recognize two distinct classes [Garey and Johnson 1979]. Algorithms for which the time complexity function is O(p(n)), where p(n) is a polynomial in n, are termed polynomial time algorithms, whereas algorithms with no polynomial bound on their complexity are called exponential time algorithms. There is a remarkable difference in growth rates between polynomial and exponential algorithms [Fig. 1]. 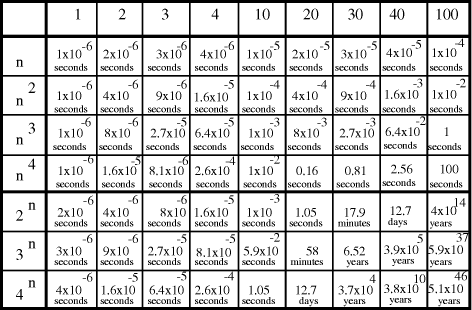 Figure 1: Time complexity functions for some polynomial (n, Page 88 Problems with polynomial algorithms are considered "good", whereas problems which are so difficult that no polynomial time algorithm can solve them are termed "intractable". The theory of NP-completeness is concerned with decision problems.
Informally, a decision problem A practical difficulty with problems in NP is that their time-complexity with a deterministic algorithm is exponential. Thus problems in NP are intractable with deterministic machines. Certain problems in NP have the property that all other problems in NP
may be polynomially reduced to them, and are termed NP-complete. If a
polynomial time algorithm can be found for any member of this
equivalence class then one can be found for all problems in NP. In
other words, if for any (problem) 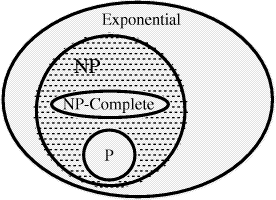 Not surprisingly the class of NP-complete problems has been the focus of considerable attention; including some recent ideas on "Quantum Computers" [DiVincenzo 1995] which could in principle solve NP problems in polynomial time. Several classical problems such as the Hamiltonian Path problem, the satisfiability problem have been shown to be NP-complete. For a more complete Page 89 discussion of these points the reader is referred to the work of Garey and Johnson [Garey and Johnson 1979]. 1.2 Molecular Computation and the HPP
The following is a simple non-deterministic algorithm for solving the HPP [Adleman 1994]:
Adleman demonstrated, using a graph small enough to be solved by visual
inspection [Fig. 3], that DNA could be used to solve the Hamiltonian Path
Problem ( 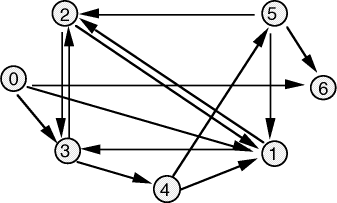 Figure 3: The directed graph used by Adleman. For 20-mer oligonucleotides were associated with each vertex Page 90 Step I is the most critical step in the algorithm as it is essential
that all paths be explored, a task with exponential time complexity on
a deterministic machine. Adleman addressed this by employing 50
picomole quantities of nucleotides corresponding to edges and the
Watson-Crick complement of vertices. While 50 picomole quantities are
minute in chemical terms, the parallelism of chemical systems is such
that they correspond to 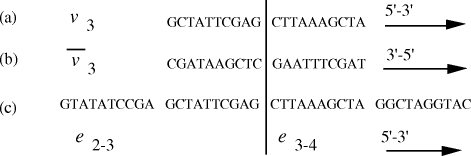 Figure 4: (a) DNA strand corresponding to vertex The remaining steps (II-V) in the algorithm were executed using
standard laboratory techniques. Polymers corresponding to paths
between the specified starting vertex 2. Scalability of Molecular Computation
2.1 Computational Capacity of Molecular Computers
In Adleman's original paper the question of the scalability of
problems solvable by molecular computation was left open [Adleman
1994]. The system contained 14 edges, each represented by 50 picomoles
of nucleotide, corresponding to a total of 5 x Page 91 computations. Concentrations could easily be scaled to yield Given this phenomenal computational capacity, and the ease with which chemical systems can be scaled, it would be easy for the non-specialist to conclude that the potential for molecular computation is practically unlimited. This is not the case; [Lineal and Lineal 1995], [Bunow 1995] and [Lipton 1995] have identified problems in the potential scalability of Adleman's method. The following analysis quantifies these limitations. Problems in NP, among them the directed Hamiltonian Path problem, have
a time complexity of  and the increase in the size of solvable problem, 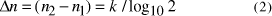
The limitations expressed in equation (2) on the capacity of molecular
computers to solve problems in NP are forcefully illustrated by
considering limits on the scale of chemical systems. In practice,
electroanalytical techniques allow for the detection of chemicals in
the picomolar range [ The largest conceivable molecular computer would involve all particles
in the universe. Of course, the amount of matter in the universe is
not known, but it may be reasonably estimated as follows: Taking
Hubbel's constant as Page 92 Assuming therefore for the purposes of illustration that the universe
contains 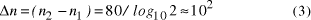 Thus the potential to increase the size of problem (in NP) which may be solved, by increasing the size of the chemical system, is very modest indeed, even when fantastic scales are involved. More relevantly, over the realizable/detectable picomolar to molar concentration range we have 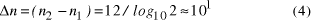 Thus while the size of molecular computers can be readily increased, the increase in the size of problems which such systems could solve is much more modest. The scalability of problem size with the size of molecular system employed is illustrated in Fig. 5. Page 93 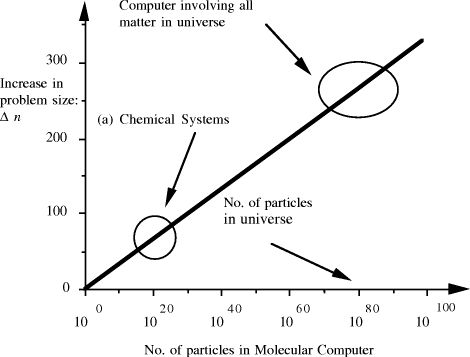 Figure 5: Increase in solvable problem size with increase in the size of the molecular computer (relative to the size of problem solvable with a system of order unity molecules). 3 Conclusion
The potential of molecular systems to increase the size of solvable
problems in NP is fundamentally limited to the order of References
[Adleman 1994] Adleman, L.: "Molecular Computation of Solutions to Combinatorial Problems"; Science, 266, (1994), 1021-1024. [Bunow 1995] Bunow, B.: "On the Potential of Molecular Computing"; Science, 268, (1995), 481-482. [DiVincenzo 1995] DiVincenzo, D. P.: "Two-Bit Gates are Universal for Quantum Computation", Phys. Rev. A, 51, (1995), 1015-1022. [Dong and Wang 1988] Dong, S., Wang, Y.: "A Nafion/Crown Ether Film Electrode and its Application in the Anoidic Stripping Voltametric Determination of Traces of Silver"; Anal. Chim. Acta, 212, (1988), 341-347. [Garey and Johnson 1979] Garey, M. R., Johnson, D. S.: "Computers and Intractability"; Freeman, New York, (1979). [Gifford 1994] Gifford, D. K.: On the Path to Computation with DNA, Science, 266, 1994, 993-994. [Lineal and Lineal 1995] Lineal, M., Lineal, N.: "On the Potential of Molecular Computing", Science, 268, (1995), 481. [Lipton 1995] Lipton, R. J.: "DNA solution of Hard Combinatorial Problems", Science, 268, (1995), 542-545. [Kaufmann 1994] Kaufmann, W. J.: "Universe"; Freeman, New York, (1994). Acknowledgments The author would like to thank Dr. T. Tuohy (Department of Molecular Genetics, Biochemistry and Microbiology, University of Cincinnati, Ohio), Dr. J. Greer Page 94 (Department of Chemistry, Trinity College Dublin) and Dr. H. Gibbons (Department of Computer Science, Trinity College Dublin), for useful discussions. Page 95
|
|||||||||||||||||
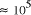 CPU years on a typical 10
MFLOP workstation. In this paper limitations on the potential
scalability of molecular computation are considered. A simple analysis
of the time complexity function shows that the potential of molecular
systems to increase the size of generally solvable problems in NP is
fundamentally limited to
CPU years on a typical 10
MFLOP workstation. In this paper limitations on the potential
scalability of molecular computation are considered. A simple analysis
of the time complexity function shows that the potential of molecular
systems to increase the size of generally solvable problems in NP is
fundamentally limited to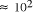 . Over the chemically measurable picomolar to
molar concentration range the greatest practical increase in problem
size is limited to
. Over the chemically measurable picomolar to
molar concentration range the greatest practical increase in problem
size is limited to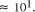
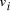 , and edges
, and edges 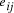 , is
there a path which starting and ending at specified vertices, visits
each remaining vertex once and only once?
, is
there a path which starting and ending at specified vertices, visits
each remaining vertex once and only once?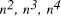 ) and
exponential (
) and
exponential (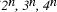 ) functions as a function of problem size, n.
) functions as a function of problem size, n.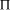 is said to belong to the class P if
there exists a Deterministic Turing Machine (DTM) program which solves
the problem in polynomial time. Non-deterministic computation differs
from deterministic computation in that a solution is exhaustively
guessed and then checked. If a correct solution to a decision problem
can be checked in polynomial time, then that problem is said to belong
to the class NP (Non-deterministic Polynomial time). Since problems
which can be solved deterministically in polynomial time can also be
guessed non-deterministically and checked in polynomial time, we can
write P
is said to belong to the class P if
there exists a Deterministic Turing Machine (DTM) program which solves
the problem in polynomial time. Non-deterministic computation differs
from deterministic computation in that a solution is exhaustively
guessed and then checked. If a correct solution to a decision problem
can be checked in polynomial time, then that problem is said to belong
to the class NP (Non-deterministic Polynomial time). Since problems
which can be solved deterministically in polynomial time can also be
guessed non-deterministically and checked in polynomial time, we can
write P  NP [Fig. 2]. It is not known whether this inclusion is
proper, that is whether NP\P is occupied.
NP [Fig. 2]. It is not known whether this inclusion is
proper, that is whether NP\P is occupied.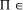 NP-complete, then
NP-complete, then 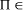 P if
and only if P = NP. Problems
P if
and only if P = NP. Problems  NP-complete may be regarded as the
hardest problems in NP. The relationship between P, NP and NP-complete
is illustrated below
NP-complete may be regarded as the
hardest problems in NP. The relationship between P, NP and NP-complete
is illustrated below NP-complete).
NP-complete).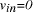 and
and 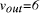 the edges 0-1, 1-2, 2-3, 3-4, 4-5, 5-6, define a Hamiltonian path.
the edges 0-1, 1-2, 2-3, 3-4, 4-5, 5-6, define a Hamiltonian path.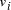 in the graph.
Oligonucleotides representing edges
in the graph.
Oligonucleotides representing edges 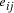 , linking vertices
, linking vertices 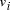 and
and 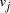 , consisted
of the 3' 10-mer of
, consisted
of the 3' 10-mer of 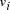 and the 5' 10-mer of
and the 5' 10-mer of 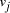 [
[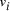 , denoted
, denoted 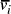 ,
serve to link compatible edges
,
serve to link compatible edges 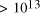 copies of each edge and vertex -
presumed sufficient to ensure that polymers corresponding to all paths
in the graph are generated.
copies of each edge and vertex -
presumed sufficient to ensure that polymers corresponding to all paths
in the graph are generated. 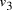 . (b) Watson-Crick
complement of vertex
. (b) Watson-Crick
complement of vertex 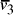 . (c) strands corresponding to edges
. (c) strands corresponding to edges 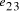 and
and 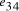 .
Nucleotide specificity in binding (A-T and C-G) ensures that vertex
.
Nucleotide specificity in binding (A-T and C-G) ensures that vertex 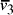 serves to
bind edges
serves to
bind edges 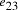 and
and 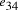 .
.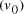 and finishing vertex
and finishing vertex 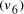 were selected (Step II) and amplified (i.e. concentration increased)
by using the polymerase chain reaction (PCR). Argose gel
electrophoresis was used to identify those polymers corresponding to
paths involving n (= 7) vertices (Step III), and the product was again
amplified using the PCR. Step IV was implemented using affinity
purification for oligonucleotide sequences corresponding to vertices
1, 2, 3, 4, 5 and 6. Any remaining polymer must correspond to a
Hamiltonian path, and a suitably primed PCR was employed to detect and
amplify any such polymer.
were selected (Step II) and amplified (i.e. concentration increased)
by using the polymerase chain reaction (PCR). Argose gel
electrophoresis was used to identify those polymers corresponding to
paths involving n (= 7) vertices (Step III), and the product was again
amplified using the PCR. Step IV was implemented using affinity
purification for oligonucleotide sequences corresponding to vertices
1, 2, 3, 4, 5 and 6. Any remaining polymer must correspond to a
Hamiltonian path, and a suitably primed PCR was employed to detect and
amplify any such polymer.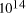 edge
nucleotides. Associating each nucleotide binding with a computation,
Adleman's molecular system yielded a total of
edge
nucleotides. Associating each nucleotide binding with a computation,
Adleman's molecular system yielded a total of 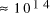
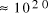 computations [
computations [
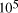 CPU years on a typical 10 MFLOP workstation.
CPU years on a typical 10 MFLOP workstation.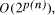 , where n is the ''size`` of the problem and
p(n) a suitably defined polynomial in n [
, where n is the ''size`` of the problem and
p(n) a suitably defined polynomial in n [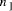 using a given computational resource is
using a given computational resource is 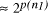 . Increasing
the scale of the molecular system by a factor
. Increasing
the scale of the molecular system by a factor 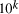 allows for the solution
of larger problems, the size of which,
allows for the solution
of larger problems, the size of which, 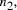 , is given by solving the
equality
, is given by solving the
equality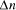 , is given by
, is given by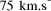
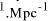 [
[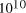 years or 4.1 x
years or 4.1 x 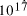 seconds. Expanding at the speed of light this gives
the volume of the universe as 7.9 x
seconds. Expanding at the speed of light this gives
the volume of the universe as 7.9 x 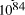 . Further assuming a universe with
critical density,
. Further assuming a universe with
critical density, 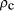
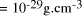 [
[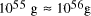 . This is the equivalent of
. This is the equivalent of 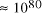 particles of mass 1
a.m.u. (taking Avogadro's number as 6.02 x
particles of mass 1
a.m.u. (taking Avogadro's number as 6.02 x 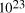 ).
).
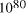 particles, it follows that the size of molecular
systems can span a maximum 80 decades, and the greatest possible
increase in solvable problem size is given by equation (2) as
particles, it follows that the size of molecular
systems can span a maximum 80 decades, and the greatest possible
increase in solvable problem size is given by equation (2) as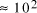 . Nevertheless, the computational capacity of Adleman's approach is
enormous, equivalent to
. Nevertheless, the computational capacity of Adleman's approach is
enormous, equivalent to 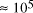 CPU years on a 10 MFLOP
workstation. The analysis is general and based on the time complexity
function, which gives the time in which a solution is guaranteed to be
found, and is therefore a worst possible case analysis; faster
solutions may be available in many cases. It is not therefore
suggested that there will be no instances where molecular computers
will prove superior to electronic computers.
CPU years on a 10 MFLOP
workstation. The analysis is general and based on the time complexity
function, which gives the time in which a solution is guaranteed to be
found, and is therefore a worst possible case analysis; faster
solutions may be available in many cases. It is not therefore
suggested that there will be no instances where molecular computers
will prove superior to electronic computers.