| Submission Procedure |
|
|
|
|||||||||||||||
Differential Ziv-Lempel Text Compression
Department of Computer Science, The University of Auckland, private Bag 92019, Auckland, New Zealand p_fenwick@cs.auckland.ac.nz Abstract: We describe a novel text compressor which combines Ziv-Lempel compression and arithmetic coding with a form of vector quantisation. The resulting compressor resembles an LZ-77 compressor, but with no explicit phrase lengths or coding for literans. An examination of the limitations on its performance leads to some predictions of the limits of LZ-77 compression in general, showing that the LZ-77 text compression technique is already very close to the limits of its performance. Keywords: text compression, LZ-77, arithmetic coding, vector quantisation Category: H.3.3 1 Introduction
It is well known that there are two main approaches to text compression, or "lossless compression". On the one hand we have the dictionary compressors, generally of the Ziv-Lempel type, which replace a later occurrence of a string or phrase by a reference to an earlier occurrence of the same phrase. On the other hand we have the statistical compressors, usually with Huffman or arithmetic coding, which exploit the uneven frequency distribution of symbols and especially the dependence of symbols upon their neighbouring contexts. More powerful compressors may use an initial dictionary compressor and following statistical compressor in cascade. There are also well-established techniques for "lossy compression", where the recovered information does not have to be an exact replica of the original. These include discrete cosine transforms, wavelets, and vector quantisation. The present work arose out of the question as to whether any of the lossy techniques might be applicable to lossless compression. It is difficult to see the relevance of cosine transforms or wavelets, which depend upon inherent regularities, or nearregularities, in the input data (and are preprocessors rather than compressors). Vector quantisation did however seem to be a useful possibility. Page 591 2 Text Compression with Vector Quantisation; Principles
In conventional vector quantisation we establish a pool of fixed length "vectors" which resemble portions of the input. We examine the next portion of the input and determine the best matching vector. The compressed output is simply the identification of this vector, together with perhaps a highly compressible approximation to the error. In text compression terms, it resembles LZ-78 compression, but with fixed-length vectors and near-matches, whereas LZ-78 uses variable-length phrases and exact matches. To combine dictionary compression and vector quantisation we start with a standard LZ-77 scan (with the usual "sliding window", etc) to determine the longest earlier phrase which matches the text to come. This earlier phrase then becomes a reference phrase for the phrase to be emitted. The current phrase is introduced with the displacement to the reference phrase. Then, for each byte, we emit the difference (exclusive-OR) between the known byte in the reference phrase and the corresponding byte in the current phrase. This difference is of course zero for as long as the two phrases match until the phrase is terminated by the non-zero code for the first non-matching byte. The term "differential Ziv-Lempel" will be used to describe the new technique. A phrase then consists of the initial position code, a sequence of zero symbols and a terminating non-zero symbol. The whole is processed through a set of arithmetic coders, one or more for the displacement and one for the data. The prevalence of identical zero symbols in the data means that they are encoded very compactly and, for reasonable phrase lengths, we can achieve good compression. The presence of the terminal byte means that it resembles the original LZ-77 compressor, rather than the later variants such as LZSS. 3 Implementation
From the above discussion it is clear that a phrase is defined only by its position and requires no explicit length. Once started, coding for a phrase proceeds until an unexpected character is encoded. Neither is there is any explicit coding for a literal. As a single literal symbol can be based on any byte whatsoever, it is simplest to just emit a displacement of 1. This bases the literal on the immediately preceding byte, forcing some non-zero code and a phrase length of 1. As an optimisation detail, we Page 592 keep track of the last occurrence of each byte value and point to that occurrence if it is sufficiently close (within 128 bytes), so defining a 2-byte phrase for a literal. Displacement coding contributes the major part of the compressed output bit stream. With arithmetic coding used for the phrase bodies, the displacements too must go through the arithmetic coder. The displacement encoding finally chosen consists of one or two components, each with its own coding model. The first component is the least-significant 7 bits of the value. If the value exceeds 127, the first component has its high-order bit set and is followed by the more-significant bits as the second component. The Ziv-Lempel parser is based on a recently-developed string matching algorithm [Fenwick and Gutmann, 1994], a description of which is included in an Appendix to this paper. For some files it is better to omit the "over-run" byte and allow the non-zero byte of the next displacement to terminate the current phrase. Literals are handled by allowing the first byte of a phrase to be non-zero. This version actually resembles a conventional LZ-77 compressor with {displacement, length} coding, but transmitting the length as a unary code. As we will see later the length coding requires only about 0.2 bits per byte and most lengths can be represented in less than 1.5 bits. The two versions will be compared later, but for now it should be noted that they are used independently, with no attempt to combine in a single compressor. 4 Performance
The actual performance on the files of the "Calgary Corpus" [Bell, Cleary and Witten, 1990] is shown [Table 1], and compared with two of the better LZ-77 style compressors, LZB [Bell, Cleary and Witten, 1990] and LZ3VL [Fenwick, 1993]. The second version, without the phrase over-runs, compares quite well with the reference LZ-77 compressors, while the first version, with over-runs, is particularly good on the binary files. The "over-run" coding is especially useful if the phrase terminates with a quite unusual byte, which would otherwise have to be emitted as a literal, many of the literals are just absorbed into the phrases and are emitted quite efficiently. GEO in particular benefits from this effect. Interestingly, PIC also benefits for the same reason. Although much of PIC is highly compressible runs of zeros, it contains some much less-compressible regions where phrases terminate on almost random Page 593 bytes and the over-runs are of considerable benefit. Text files on the other hand tend to have sequences of phrases with few intervening literals and for these the more efficient phrase termination of the "no-overrun" coding is better. PIC also gains considerable benefit from its very long phrases (7 phrases for the first 50,000 bytes, and one of over 36,000 bytes at the end). Several other files (NEWS, OBJ1, PROGP, TRANS) also have phrases exceeding 1000 bytes.
File diffLZ diffLZ LZB LZ3VL
overrun n-ovm
BIB 3.22 3.22 3.17 3.00
BOOK1 4.13 3.88 3.86 3.65
BOOK2 3.47 3.27 3.28 3.07
GEO 5.34 6.36 6.17 5.93
NEWS 3.83 3.78 3.55 3.47
OBJ1 4.48 4.83 4.26 4.08
OBJ2 2.92 3.17 3.14 2.96
PAPER1 3.47 3.29 3.22 3.08
PAPER2 3.67 3.42 3.43 3.23
PIC 1.02 1.16 1.01 1.04
PROGC 3.34 3.19 3.08 2.97
PROGL 2.23 2.15 2.11 2.03
PROGP 2.31 2.15 2.08 2.01
TRANS 2.14 2.13 2.12 1.96
AVERAGE 3.26 3.26 3.18 3.03
Table 1. Performance, compared with other good LZ-77 compressors Attempts to combine the two versions, switching according to data statistics, were totally unsuccessful. It is easy to separate GEO as a special case, but much much harder to detect that PIC needs the overrun coding. The two sets of results are therefore just presented separately, with no attempt at a combined version. The version described so far was only an initial attempt at incorporating vector quantisation techniques, full quantisation allows for longer strings with continuation after mismatches. A "fuller VQ" version was attempted, allowing multiple mismatches and with phrases stopping on a sequence of fewer than about 5 matched bytes. It gave an improvement of about 3% on the file GEO, but was 3-20% worse for other files and will not be considered further. It is useful only where long phrases differ only in one or two internal bytes, and few real files are like that. Page 594 5 Analysis of the Differential LZ Compression Performance
Analysis of the performance of the differential Ziv-Lempel compressor, and in particular the reasons for its slightly inferior performance compared with standard compressors, led to some useful insights concerning the basic limits of LZ-77 compression. Initially we deal only with the new technique, and specifically the version with phrase overruns, but the analysis is later extended to more-conventional LZ-77 compression. We start with [Table 2] containing some general statistics from the compression of the file PAPER1 of the Calgary Corpus, using the diffLZ compressor. (The "output bits" includes the End-of-File coding, which are not included in the displacement and data values.) Input bytes 53,161 Output bits 184,527 Displacement bits 98,590 Data bits 85,921 Total phrases 8,224 Avg. phrase length 6.46 Longest phrase 91 Frequencies of displacement lengths - Length 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Frequ. 429 161 278 341 430 407 512 464 579 701 856 990 1061 1015 Table 2. Compression statistics, PAPER1 The average phrase length is 6.46 bytes, consisting of 1 terminal byte and 5.46 zero bytes.
Page 595 Encoding the whole file should then require -
phrase terminators 8224 at 9.68 bits 79,608 bits
phrase body (53161 -8224) at 0.205 bits 9,212 bits
sub-total (Phrases) 88,820 bits
displacement 76,357 bits
TOTAL 165,1 77 bits
The phrases themselves actually need 85,921 data bits, which is 3.5% less than the predicted 88,820. The difference arises because the terminating symbols are not evenly distributed over the possible 127 values, some can be encoded more efficiently, so reducing the overall number of code bits. The displacement coding however requires 98,590 bits, which is 29% greater than the apparent best coding, the average displacement length is 11.99 bits, compared with the "ideal" of 9.28. The difference arises from the need to specify the displacement length, as well as the value. ln practice, the models absorb the statistics on the component lengths and include it implicitly within the coding. The displacements could be coded as the couple {length, value} with the most significant 1-bit omitted, giving an average displacement value of 8.28 bits. The entropy of the lengths (using the frequencies of Table 2) is 3.64 bits, giving an average displacement encoding length of 3.64+8.28 = 11.92 bits. The displacement coding achieves 1 1.99 bits average length, which is within 0.6% of the ideal. It is obvious that little improvement is possible. 6 The Relevance of Variable Length Codes
It is useful to consider the general relevance of variable-length integer codings, as given in [Bell, Cleary and Witten, 1990]. These usually use some form of variable-size overhead to allow small values to be coded compactly, but at the cost of less efficient coding for large values which often need a larger overhead. This is precisely the opposite effect of what we want for displacements! Most of the displacements are large, and should be encoded with low overhead. The short displacements, being infrequent, can be coded with larger overheads. Thus the conventional variable-length codes are quite inappropriate for displacements. Very long displacements predominate and even transmitting the raw 14-bit binary value is Page 596 relatively efficient in comparison with a compact coding of the displacement. Precisely the opposite situation applies for encoding the phrase lengths in conventional LZ-77 compression. The shorter phrases are much more frequent with relatively little compression gain and must be coded as compactly as possible. The longer phrases are less frequent, give much more benefit, and can be coded inefficiently with little penalty. 7 Interpretation as an Arithmetic Code
Although the technique has been introduced as a derivative of LZ-77 compression, it can be viewed as high context arithmetic compressor. An LZ-77 parse is used to find the best following context including the next byte and the coder then emits from this context, with 100% certainty, for as long as possible. This is in contrast to conventional high-order arithmetic compression where we establish a preceding context for each byte, and emit probabilistically from this context. The output from any high order arithmetic compressor consists of two intermingled data streams, one conveying data and one information on the contexts. Thus in a compressor which allows escapes to lower order contexts, the code for every byte must include the information "this is a symbol with some probability" (i.e. data) and "this is not an escape" (context). Explicit escape codes will reverse these meanings. While data in a high context arithmetic coder can be emitted at about 1 bit per byte for many files, we often find that more information is required for context control. Thus context management is more expensive than data encoding proper. Exactly the same situation applies here. Because the LZ-77 parse establishes a precise context, data can be emitted with zero cost - all of the coding is concerned with context management. The normal "data encoding" uses about 0.2 bit/byte to signal "continue in this context". With some expense it notes the end of the phrase and then requires a dozen or more bits to establish a new context, in all about 20 bits to switch between contexts. The context management, rather than the data, sets the compression performance. 8 Performance Limits of Standard LZ-77 Compression
We can extend the above analysis to conventional LZ-77 compression. The Page 597 comparisons are somewhat "apples and oranges", because the differential (or vector quantising) compressor alters the definition of an LZ-77 phrase by always over-running by one byte. We may also note the well-known effects of buffer size on LZ-77 performance, which means that we might not always compare like with like. There are also various subtle differences in details of the encoding, such as the LZ3VL compressor coding displacements to the end of the phrase rather than to its start, and considerable variations within files, so that the overall statistics might not be completely representative. However, the calculations do appear to give a reasonable indication of the possible performance of LZ-77 compression.
input literals phrases predicted displ disp len phr len
bytes displ bits avg entropy entropy
BIB 111,261 7,928 14,279 165,132 11.565 2.898 3.247
BOOK1 768,771 38,179 142,028 1,656,514 11.663 2.874 2.951
BOOK2 610,856 31,167 89,544 1,005,560 11.230 3.076 3.347
GEO 102,400 24,829 23,316 239,324 10.264 3.228 1.383
NEWS 377,109 41,541 53,589 584,734 10.911 3.189 2.780
OBJ1 21,504 6,017 2,238 18,633 8.326 3.498 1.639
OBJ2 246,814 29,110 26,237 247,772 9.444 3.503 2.760
PAPER1 53,161 3,611 7,460 80,716 10.820 3.185 3.251
PAPER2 82,199 4,295 12,925 145,911 11.266 3.022 3.251
PIC 513,216 22,761 16,655 162,731 9.771 3.130 2.990
PROGC 39,611 3,226 5,081 51,914 10.217 3.343 3.304
PROGL 71,646 3,158 6,483 65,374 10.084 3.357 3.726
PROGP 49,379 2,629 4,290 41,079 9.576 3.436 3.525
TRANS 93,695 5,713 7,256 74,326 10.243 3.375 3.378
Table 3. Observed parameters from LZ-77 compression An LZ-77 compressor (with greedy parsing, 2-byte minimum phrase length and 16 K buffer) was instrumented to report various statistics on compressing the files of the Calgary Corpus, producing the results in [Table 3], with consequent predictions given in [Table 4]. The two basic assumptions are- 1. The phrase is located by an actual displacement, rather than a position in some complex data structure, and 2. A phrase is encoded as the triple {length, displ_precision, displ_value}, where the phrase length and displ_precision are entropy encoded and displ_value is the actual bits following the most-significant 1 of the displacement. Page 598 This phrase encoding should be very close to the optimal coding of the phrase definition. Conventional LZ77 encoding (more correctly LZ-SS) uses a flag bit to indicate a literal or phrase; here we use a reserved length, most sensibly 1, and encode a literal as {1, literal}. This coding is slightly less efficient for literals, but saves one bit when encoding the usually more frequent phrases. Much of the calculation parallels that given earlier for PAPER1. In more detail, consider the file BIB which produced 7,928 literals and 14,279 phrases. The weighted sum of the minimum displacement lengths gives a "predicted displ bits" and the average displacement length. The entropy of the displacement lengths gives the minimum cost of specifying the displacement lengths. The phrase length entropy is similarly calculated from the distribution of phrase lengths. The average length of a phrase is then 10.56 + 2.90 +3 .25 = 16.71 (omitting
the most-significant 1-bit of the displacement reduces the
displacement length by 1, from 11.56 to 10.56). A literal is encoded
as 8 bits plus information to specify one of 7,928 literals out of a
total of 22,207 cases, or Two points are apparent from this study. The first is that for most files one or other of the LZ-77 compressors is within 10% of the apparent limit, with some being within 5%. There appears to be little possible gain beyond what has been achieved already in LZ-77 compressors. The new diffLZ compressor attains the predicted limit for GEO. The second point is that the phrase length is nearly constant. The
average over the whole corpus is 15.6 bits, with a standard deviation
of 1.2 bits. Ignoring the binary files gives a length of an LZ77 phrase usually needs about 16 bits to encode. What really varies between files is the average phrase length. Those with more long phrases are more compressible and with more short phrases less compressible; the Page 599 cost of encoding a phrase is approximately constant. The main limitation is in the coding of the displacement. This is essentially a large random number and not very much can be done to optimise its coding.
pred avg pred total pred total pred limit best of LZB, perf. rel
phrase bits literal bits phrase bits bit per byte LZ3VL, diffLZ to limit
BIB 16.71 75,205 238,602 2.80 3.00 94%
BOOK1 16.49 390,907 2,341,758 3.56 3.65 97%
BOOK2 16.66 310,220 1,491,176 2.95 3.07 96%
GEO 13.88 222,353 323,510 5.33 5.34 100%
NEWS 15.88 381,985 850,993 3.27 3.47 94%
OBJ1 12.46 50,881 27,892 3.60 4.08 90%
OBJ2 14.71 259,865 385,868 2.62 2.92 89%
PAPER1 16.27 34,725 121,270 2.94 3.08 95%
PAPER2 16.54 42,974 214,213 3.13 3.23 97%
PIC 14.89 200,120 248,010 0.88 1.02 86%
PROGC 15.86 30,210 80,605 2.80 2.97 94%
PROGL 16.17 30,349 104,811 1.89 2.03 93%
PROGP 15.54 24,702 66,654 1.86 2.01 92%
TRANS 15.99 52,461 116,067 1.80 1.96 92%
Table 4. Predictions ofbest LZ-77 compression An interesting observation is that the incompressible files tend to require fewer bits to encode a phrase. Not only are their phrases shorter, requiring fewer length bits to encode, but the shorter phrases are more likely to be matched closer to the current position and with shorter displacements as well. The deficiencies in the new compressor are, as might be expected, almost entirely in the definition of the phrase length, although the data over-runs do reduce the number of phrases and allow more efficient coding of infrequent literals. 9 Conclusions
We have described a novel combination of Ziv-Lempel, arithmetic and vector quantisation to produce a text compressor of good general performance, and excellent performance on some files. It is unique in that while based on LZ77 parsing, it has no explicit phrase length or literal encoding. Page 600 Investigations of the performance of this compressor led to a wider study of LZ77 compression and firm indications that text files cannot be compressed to better than about 3.0 bits/byte with LZ77 compression. The best extant LZ77 compressors are already very close to this predicted limit. References
[Bell, Cleary and Witten, 1990]. T.C.Bell, J.G. Cleary, and I.H. Witten, Text Compression, Prentice-Hall, Englewood Cliffs, NJ 1990 [Fenwick, 1993]. P.M. Fenwick, "Ziv-Lempel coding with multi-bit flags", Proc Data Compression Conference, DCC-93, Snowbird, Utah, Mar 1993 [Fenwick and Gutmann, 1994]. P.M. Fenwick and P.C. Gutmann, "Fast LZ77 String Matching", Dept of Computer Science, The University of Auckland, Tech Report 102, Sep 1994 APPENDIX. The Gutmann fast string matching algorithm
A recent study by Gutmann has examined the performance of many string-matching algorithms, from the very simple to very complex. He found that while it is easy to devise extensive data structures to minimise the number of comparisons, it is only too easy to lose out from the overheads of maintaining and traversing the data structure. It may be better to use a simple structure with frequent, but inexpensive, comparisons. His preferred algorithm is described here. We maintain a conventional LZ buffer as a simple byte array. pairs of adjacent bytes are hashed and used to index a table which defines links through the array, connecting byte pairs of like hash values. When looking for a string we hash the first bytes of the string and then trace along the chain corresponding to that hash value. The chain must include all occurrences of those first bytes (plus any others which collide in the hash table). So far it is a standard simple LZ buffer. Assume that at some stage we have a longest match of length Page 601
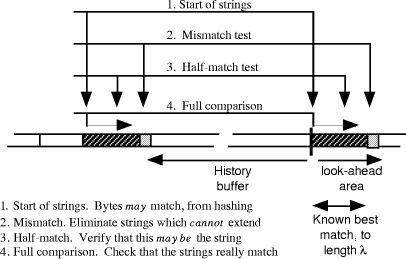 Gutmann's experiments show that about 50% of possible phrases are eliminated on the mismatch test and that fewer than 10% survive the half-match as well and need a full comparison. Testing a given candidate string then requires only the following steps, most of which are simple and fast - 1. Check that this position is still valid (not beyond the end of the hash chain) 2. Compare the mismatch bytes 3. Compare the half-match bytes 4. Do a full comparison of the two strings 5. Step to the next position in the hash chain A further refinement, which is not used here, is to select as the half-match byte one with a low probability. This approximately halves the number of full comparisons for files such as PIC and GEO. Page 602
|
|||||||||||||||||
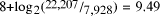bits, giving 75,205 bits for
literals over the whole file. We predict a total of 16.71x14,279
phrase bits, giving a total of 313,807 bits and 2.82 bits per
byte. The best available compressor delivers 3.00 bits/byte, or 94% of
the predicted limit. Entropy-encoding literals might allow some more
compression, but it is unlikely to be significant because it is only
the less-probable values which appear as literals - the more-frequent
ones, which would benefit from statistical coding, tend to appear
within phrases anyway.
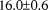bits. This gives a useful rule of thumb for LZ77 compression, that
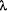, and
are looking for a string of length 
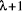. As there is no benefit in
considering any string with length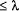 
, we first look at the
"mismatch" byte in position 
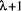, one beyond the known best length. If
that byte does not match, the position cannot possibly give a better
match. If that byte matches, we then compare "half-match" bytes at
about the midpoint of the known best string. This byte is simply a
representative candidate of the strings. Only if the mismatch and
halfmatch comparisons succeed do we do a full byte-by-byte comparison
of the two strings. If the match succeeds to length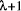
, we then extend the match as far as possible.
