| Submission Procedure |
A Robust Affine Matching Algorithm Using an Exponentially Decreasing Distance Function
Institute for Computer Graphics Technical University of Graz Muenzgrabenstr. 11 A-8010 Graz, AUSTRIA email: pinz@icg.tu-graz.ac.at Abstract: We describe a robust method for spatial registration, which relies on the coarse correspondence of structures extracted from images, avoiding the establishment of point correspondences. These structures (tokens) are points, chains, polygons and regions at the level of intermediate symbolic representation (ISR). The algorithm recovers conformal transformations (4 affine parameters), so that 2-dimensional scenes as well as planar structures in 3D scenes can be handled. The affine transformation between two different tokensets is found by minimization of an exponentially decreasing distance function. As long as the tokensets are kept sparse, the method is very robust against a broad variety of common disturbances (e.g. incomplete segmentations, missing tokens, partial overlap). The performance of the algorithm is demonstrated using simple 2D shapes, medical, and remote sensing satellite images. The complexity of the algorithm is quadratic on the number of affine parameters. Keywords: Affine Matching, Spatial Registration, Information Fusion, Image Understanding 1 Introduction
In Computer Vision, the establishment of correspondence between different sources of visual information is an important issue. Affine matching has mainly been used for image to model matching (e.g.[Beveridge et al., 1990], [Collins and Beveridge, 1993], see Fig. 1.a) and for image to image matching (e.g. [Zabih and Woodfill, 1994], [Collins and Beveridge, 1993], [Flusser and Suk, 1994], see Fig. 1.b), often with the purpose of spatial registration of images [Brown, 1992]. Our motivation for this work is driven by the idea of a general framework of "Information Fusion in Image Understanding" [Pinz and Bartl, 1992a], [Pinz and Bartl, 1992b], [Bartl et al., 1993]. In order to be able to deal with multiple visual information on all levels of abstraction, proper transformations of three different kinds are required:
1. spatial (coordinate) transformations, Information that can be compared with respect to the above transformations is said to be in registration. While recent relevant work on fusion simply assumes Page 614 prior registration of the source images (e.g.[Maître,1995, Clement et al., 1993], [Burt and Kolczynski, 1993], [Toet, 1989], we want to fuse visual information without the requirement of prior manual registration. In this paper we concentrate on the following case: - different source images, - different coordinate systems. Spatial registration can be achieved by a conformal transformation (4 affine parameters), - the match is established at the ISR level (intermediate symbolic representation [Brolio et al., 1989]), see Fig. 1.c. 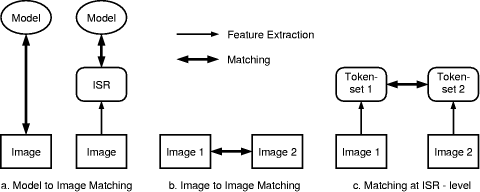
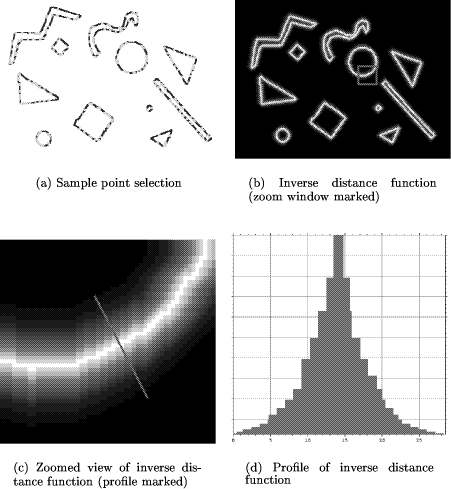
ISR supports associative retrieval, spatial relations, and multi-level representations and is well suited for many image understanding applications [Draper et al., 1993]. A so-called token (`image event') represents one of the following `location' features: a point, a line, a chain of points, a polygon, and a bitmap representing a region. For each token, an arbitrary number of additional features can be calculated (e.g. shape, spectral and texture parameters). Related tokens are collected in a `tokenset'. Figure 2 gives a simple example for an image of a purely 2-dimensional scene with 2D shapes (`shapes' image Fig. 2.a). A region-based segmentation of this image results in a tokenset of 11 bitmaps visualized in Fig. 2.b. The process of segmenting an image into a tokenset is covered in detail in [Pinz, 1994]. In the context of this paper we want to emphasize that the intelligent use of ISR (e.g. application of constraints, perceptual grouping, elimination of irrelevant tokens) often leads to relatively sparse tokensets, thus reducing the amount of data dramatically (as compared to the pixels of the original image). This results in a substantial reduction of computational complexity for the subsequent process of matching of two different tokensets (e.g. 11 tokens versus 258000 pixels for Fig. 2). Consider the situation sketched in Fig. 1.c: Starting from two different images of the same scene, segmentation and feature extraction processes are used to create two tokensets. Under certain assumptions, the spatial relationship between the tokensets (and the images) can be modeled by an affine transformation.  This holds for 2-dimensional scenes, as well as for planar structures in 3D scenes (see [Collins and Beveridge, 1993], [Grimson et al., 1994], [Flusser and Suk, 1994] for more detail): 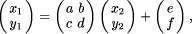 with 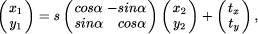 consisting of a translation vector t = While Grimson et.al. [Grimson et al., 1994] distinguish between two different types of affine matching algorithms (hypothesize and test and geometric hashing), Collins and Beveridge [Collins and Beveridge, 1993] find four categories (key-feature algorithms, generalized Hough transformations, geometric hashing, and constraint-based tree search). Our algorithm could be categorized as a hypothesize and test approach which allows for many-to-many mappings between features. A review of similar and related work in the area of object recognition, where the task is to determine the transformation between a model and an image, reveals many recent publications (e.g.[Basri and Jacobs, 1995, Rucklidge, 1995]), as well as fundamental work dating back to the mid 80s (e.g. [Ayache and Faugeras, 1986, Borgefors, 1988]). The general approach of Page 616 performing a search in transformation space for the best matching transformation, which is also followed in this paper, has been explored in the past, e.g. for the purpose of locating images of rigid 3D objects. The algorithm proposed by Cass [Cass, 1992] takes into account the inherent geometric uncertainty of data features when matching a model to image data. By assigning an uncertainty region to each data feature he restricts the space of possible transformations and arrives at an algorithm of polynomial complexity. However, his algorithm seems less suited for the matching of rather dissimilar patterns (like Fig. 11 or Fig. 14). Lowe, [Lowe, 1987] also matches 3D rigid model data with 2D images, exclusively using edges as primary features, which are subsequently segmented, perceptually grouped, and matched. His algorithm applies Newton's method and requires partial first order derivatives. Perhaps closest to our work we found the `Hierarchical Chamfer Matching' algorithm by Borgefors [Borgefors, 1988] using a quadratic distance function to measure the goodness of match. While she briefly mentions the general applicability of the method to many different kinds of features, she only reports on the matching of edges. In this context we want to point out that our approach concentrates on the capability of using any type of tokens (points, edges, lines, regions, as well as quite specialized and application oriented types, e.g. the blood vessels described in section 3.1.2, which are modeled as tubes), and thus could best be described as `affine matching of intermediate symbolic representations' or `affine matching at ISR level' (see Fig. 1.c). The paper is organized as follows: We start with a detailed description of the affine matching algorithm, proceed with several experiments on the recovery of simulated transformations and `real' transformations between data sets originating from different sources, and finally discuss the performance of the algorithm. 2 The Affine Matching Algorithm
We are given two sets of tokens. One is the source and the other the target tokenset for the affine matching algorithm. The aim now is to find the conformal transformation to bring the source tokenset into spatial registration with the target tokenset. The way we chose to tackle this problem is to formulate it as the maximization of an objective function as defined below. 2.1 The Objective FunctionThe target tokenset is first transformed into a binary image with the resolution of the image depending on the required accuracy. Region tokens are not drawn with all their pixels set but just the border pixels, as the border determines the position, scale and rotation. Now for each background pixel we calculate an inverse distance
function (see section 2.2) to its closest foreground pixel
(i.e. to the pixel belonging to the tokenset). In order to keep the
computational burden low, we do not transform the whole source
tokenset with the transformation in question, but just a number of
extracted sample points (described in section 2.4). The
objective function to be maximized is then defined as Page 617 with There are, of course, some limitations on the allowable range for the translation, scale and rotation parameters. Otherwise a scale of zero would always be optimal in the sense that it would transform all sample points onto one position and would result in a maximum value for the objective function if that position is on the target tokenset. The limitations on the parameter range are a first coarse guess on the expected transformation values provided by the user and are implemented as strong penalty terms in the evaluation of the objective function. 2.2 The Inverse Distance Function
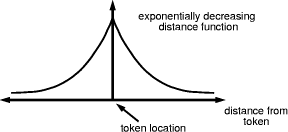
The first distance function that might come into one's mind is the Euclidean distance between a background pixel and its nearest foreground pixel (or to be more precise: an inverse Euclidean distance having a maximum at the location of the foreground pixels and then falling off like a 45 degree ramp towards the background). However, this will in general lead to an objective function which is not very robust and which can easily be fooled by points resulting from an incorrect transformation which do not hit the target tokenset but are just somewhat nearby. Fig. 3 depicts such an example.
Figure 3: Due to a segmentation error a feature is missing in the target tokenset. Even though the sample points from the wrong feature do not match the target feature exactly, they achieve a higher score in the matching process simply because they are more numerous. We want to have those points which hit the target tokenset exactly (within the accuracy of the image resolution) to obtain a higher weight than those which Page 618
Figure 4: An exponentially decreasing distance function gives stronger weights to points very close to the true location and thus makes the matching more robust. are just close to the true position. One can achieve such an effect by choosing an inverse distance function that falls off exponentially with the distance from the foreground pixels (see Fig. 4). In such a case the number of transformed points arising from an incorrect transformation and being close to the true position must be much higher to result in a value for the objective function that is larger than what we would have computed by using the correct transformation. Hence, such a choice of the distance function will make the whole matching procedure more robust against outliers. Figure 5.b-d show an intensity coded distance function corresponding to the tokens of Fig. 2.b. 2.3 Optimization Procedure
Now that we are able to compute an objective function for every parameter vector of the conformal transformation, we have formulated the problem of spatial registration as that of finding the global optimum of a function. There exist many different methods for finding such an extremum in the literature. Most of them deal with cases where the global optimum is hid among many local extrema and considerable effort is spent to overcome the problem of getting stuck in one of those local extrema. However, in general, these methods require along time to converge and still do not guarantee to arrive at the global optimum. Provided we are dealing with tokensets that are not too dense (a requirement we can often fulfill by choosing the proper parameters for the low-level segmentation tasks that produce the tokensets), we can, however, assume that the chosen objective function will not have that many local extrema. It will exhibit a structure that varies smoothly over large portions of the parameter space. These considerations lead us to an optimization procedure where we simply start local optimization from a couple of different seed points and take the extremum with the highest score. Even though this procedure does not assure to arrive at the global optimum, it performed well in practice. Furthermore, it has the advantage that we can use fast and reliable local optimization procedures like Powell's method (see [Press et al., 1992]. 2.4 Extraction of Sample Points
A tokenset can contain various types of tokens, including points, lines and regions. Generally, the sample points are distributed randomly over the tokenset. Page 619
In some cases there are substructures within the tokenset that are of higher significance than others and should, therefore, get a higher share of the total number of sample points. An example for such a structure are the vessels of Fig. 9.b. There are many short vessels but just a few long and significant ones. In order to achieve a selective distribution of sample points a weight (belief value) can be assigned to substructures of the tokenset. The actual attachment of the weight to individual tokens is up to the module generating the tokensets and is not the concern of the matching process. Tokens having a higher weight will be treated with preference when the selection of sample points takes place. This causes the matching algorithm to give priority to such substructures in finding the correct match. Figure 5.a shows an example for the sample point selection. Page 620 2.5 General Outline of the Algorithm
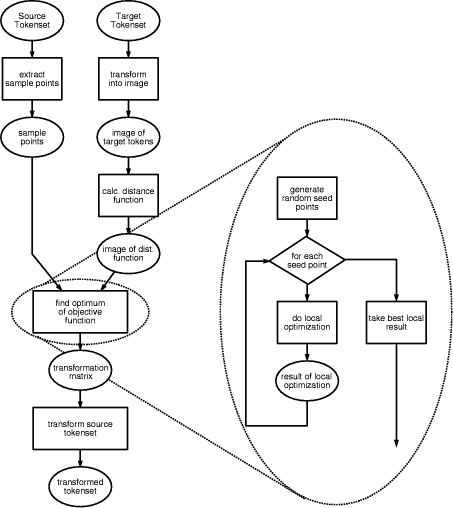
The general outline of the algorithm is depicted in
Fig. 6. The structure is simple and easy to implement. One
can use any local optimization technique often available from standard libraries.
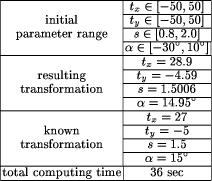
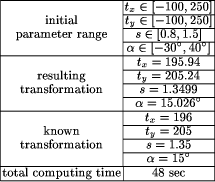
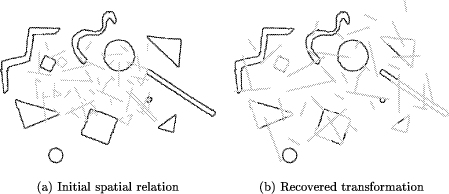
3 Experimental ResultsWe tested the algorithm on a variety of different image examples. Some of them were generated by simulating a conformal transformation, whereas others stem from real multisource applications of medical imaging and remote sensing. Page 621 3.1 Simulated TransformationsSimulated test data was used in order to provide the exact ground truth for evaluating the accuracy of the algorithm and to incorporate some of the common disturbances generally found in many applications (like fragile segmentation, only partial overlap, etc.). 3.1.1 Shapes ImageThe first experiment was performed on a simple shapes image (Fig. 2.a). The extracted tokenset (depicted by Fig. 2.b) was disturbed by erasing some of the tokens and adding artifacts corresponding to a noisy feature extraction process (Fig. 7.a). The resulting tokenset was matched by our algorithm onto a tokenset (Fig. 7.b) which in turn was obtained by transforming the original tokens with a known conformal transformation. Figure 8.a illustrates the initial spatial relation of the two sets and Table 1 summarizes the used transformation parameters and the result computed by the proposed method. By visually inspecting Fig. 8.b one can confirm that the algorithm performed well. 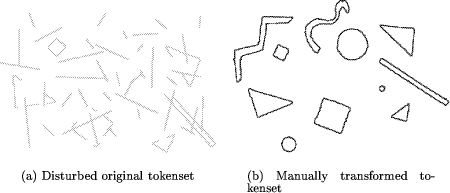 3.1.2 Medical ImageOur second experiment with known transformations was performed on an image from a medical application. In contrast to the shape experiment, the image itself and not the extracted tokenset was transformed. An algorithm for the extraction of vessel structures modeling vessels as tubes of varying radius [Huang and Stockman, 1993] was applied onto both images to provide the tokensets. The vessel extraction was done with slightly varying input parameters in order to simulate the fragility of low level segmentation procedures. Figure 9 and 10 illustrate the initial data set, the vessel segmentation results and the matched tokensets. Again visual inspection and comparison of the data in Table 2 reveals good performance of the affine matching algorithm. Page 622
  Page 623 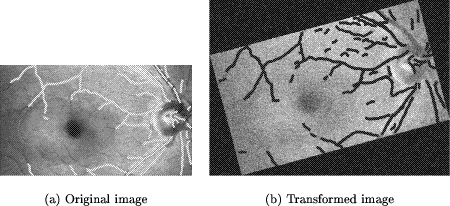 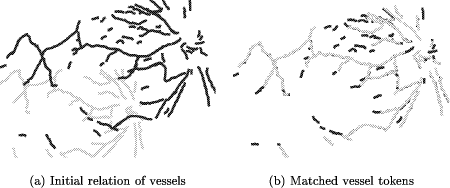 3.2 Real Data SetsThe real data sets consist of images that exhibit a mutual transformation closely resembling (but not exactly matching) a conformal transformation. Since the 'correct' conformal transformation is unknown, we compare the result of our algorithm to 'measured' transformations. They are obtained by manual selection of corresponding points in the two images and calculating the affine parameters by least-squares adjustment. 3.2.1 Medical Data SetThe medical data set shows images of the human retina acquired by a Scanning Laser Ophthalmoscope (SLO)[Webb et al., 1987]. The images were generated using different laser sources and examination methods (e.g. argon-blue laser, Page 624 fluorescein angiography). In order to detect pathological changes and to perform the appropriate treatment [Pinz et al., 1995a], [Pinz et al., 1995b] they have to be spatially registered. Similar to our experiment using a simulated transformation (section 3.1.2), the features used for registration are again the vessels on the eye background. The reason for using them is that they are the only retinal features visible in all images acquired by the SLO. As with our previous experiments, Figure 11 and Fig. 12 show the initial data, the tokensets and the result of the matching process. Table 3 shows that the results of the affine matching are very close to the manually 'measured' transformation. 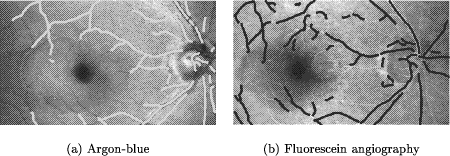 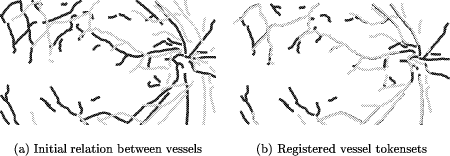 Page 625 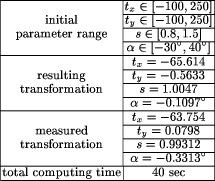 3.2.2 Remote Sensing Data SetFinally, we want to give an application example from satellite image
remote sensing. Figure 13 shows the near infrared
(approx. 0.8 
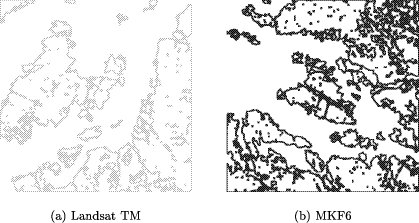 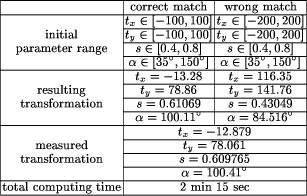 Figure 15 shows the results for two different runs of the affine matching algorithm, the corresponding parameter settings are given in Table 4. The Landsat tokenset is transformed to the geometry of the MKF6 tokenset. In the case of the correctly recovered conformal transformation (Fig. 15.a) we show an overlay of both images and tokensets, while Fig. 15.b shows an overlay of the correctly transformed Landsat image and the incorrectly recovered Landsat tokenset over MKF6 image and tokenset. Page 627 
algorithm. There are several preconditions on the data which are required for the algorithm to work reliably: -Rough estimates for the scaling s should be given. It is much better to select source and target tokenset in a way that s 1 (i.e. the source tokenset is scaled down), so that the majority of selected sample points will be transformed to the interior area covered by the target tokenset. -A reasonable amount of overlap of the two tokensets is required, otherwise the algorithm will only work in cases of very sparse tokensets with very dissimilar shapes. -Both tokensets have to be sparse. In the example shown by Fig. 15.b, the information in the upper right corner of the target tokenset (Fig. 14b) is too dense. If we allow for a wide range of translations and scalings, the algorithm will be 'attracted' by this dense area, trying to map most of the source tokenset onto it. -Up to a certain level of complexity, dense tokensets can still be handled, if the number of sample points is increased accordingly. In the experiments shown here, we used 300 sample points for the shapes and for the medical images, and 1500 sample points for the remote sensing data set. -As with any other affine matching approach, the algorithm will have difficulties with regular periodical structures (parallel lines, grids, etc.). If these conditions are fulfilled, the algorithm has already shown to perform well for a wide variety of visual data. Concerning the complexity of the proposed matching algorithm, it goes linear with the number of sample points and seed points, and quadratically with the number of parameters of the affine transformation. Page 628 The concept of 'Affine Matching at the ISR-level' introduced in this paper seems to be a general and promising approach for many correspondence problems encountered in Computer Vision. 5 Implementation Details
The computing times given for the experiments were obtained on a Silicon Graphics Power Challenge L (2 x R8000 75MHz processors) running IRIX 6.01. The code was implemented using the KBVision image processing package and no effort was spent on optimizing the procedure for speed. As mentioned above the number of sample points was 300 for the shapes and medical images and 1500 for the remote sensing data set. We used 50 seed points for the optimization procedure for all the experiments. 6 Conclusion and OutlookIn this paper, a general method for affine matching at the level of intermediate symbolic representation (ISR) was introduced. The method is easy to implement and to parallelize. Since most applications have to deal with the extraction of some kind of significant features, which can conveniently be represented at the ISR level, the method should be of common interest. It could be used in many industrial, medical and remote sensing applications. Our algorithm relies on the coarse correspondence of tokens extracted from images. It does not require the establishment of point correspondences. If the tokensets are kept sufficiently sparse, low level features (e.g. edge elements) can directly be used without the necessity of further processing (e.g. grouping edge elements into straight lines, ribbons or corners). Since belief values guide the probability that a certain token is selected for correspondence, and many-to-many correspondences are possible, the method is very robust against a broad variety of common disturbances (e.g. incomplete segmentations, missing tokens, partial overlap). An extension of the algorithm to recover a general 6 parameter affine transformation is straightforward and computationally feasible. Multisource visual information fusion (data fusion [Abidi and Gonzalez, 1992], consensus vision [Meer et al., 1990]) is a field of growing interest and importance. The comparison and integration of information from several sources without the necessity of prior (manual) spatial registration is still an issue of ongoing research. In this context, the affine matching algorithm constitutes just one module for spatial reasoning in a complex framework for Information Fusion in Image Understanding (proposed in [Pinz and Bartl, 1992a]). Acknowledgments
This work was supported by the Austrian 'Fonds zur Foerderung der wissenschaftlichen Forschung' under grant S7003. We thank Renate Bartl and Werner Schneider (Univ. f. Bodenkultur Vienna) for putting the original Landsat and MKF6 images and the classifications of these images at our disposal. Several constructive comments by the anonymous referees helped to improve this paper and are gratefully acknowledged. Page 629 References
[Abidi and Gonzalez, 1992] Abidi, M. and Gonzalez, R. editors (1992). Data Fusion in Robotics and Machine Intelligence. Academic Press. [Ayache and Faugeras, 1986] Ayache, N. and Faugeras, O. (1986). HYPER: A new approach for the recognition and positioning of two-dimensional objects. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8(1):44-54. [Bartl and Pinz, 1992] Bartl, R. and Pinz, A. (1992). Information fusion in remote sensing: Land use classification. In Multisource Data Integration in Remote Sensing for Land Inventory Applications, Proc Int.IAPR TC7 Workshop, pages 9-17. [Bartl et al., 1993] Bartl, R., Pinz, A., and Schneider, W. (1993). A framework for information fusion and an application to remote sensing data. In Poeppl, S. and Handels, H., editors, Mustererkennung 1993, Informatik aktuell, pages 313-320. Springer. [Basri and Jacobs, 1995] Basri, R. and Jacobs, D. (1995). Recognition using region correspondences. In Proc. 5.ICCV, International Conference on Computer Vision, pages 8-15. [Beveridge et al., 1990] Beveridge, J., Weiss, R., and Riseman, E. (1990). Combinatorial optimization applied to variable scale model matching. In Proc. of the 10th ICPR, volume I, pages 18-23. [Borgefors, 1988] Borgefors, G. (1988). Hierarchical chamfer matching: A parametric edge matching algorithm. IEEE Transactions on Pattern Analysis and Machine Intelligence, 10(6):849-865. [Brolio et al., 1989] Brolio, J., Draper, B., Beveridge, J., and Hanson, A. (1989). ISR: A database for symbolic processing in computer vision. IEEE Computer, pages 22-30. [Brown, 1992] Brown, L. (1992). A survey of image registration techniques. ACM Computing Surveys, 24(4):325-376. [Burt and Kolczynski, 1993] Burt, P. and Kolczynski, R. (1993). Enhanced image capture through fusion. In Proc. 4.ICCV, pages 173-182. [Cass, 1992] Cass, T.A. (1992). Polynomial-Time Object Recognition in the Prescence of Clutter, Occlusion, and Uncertainty. In Sandini, G., editor, Computer Vision - ECCV'92, pages 834-842. Springer-Verlag. [Clement et al., 1993] Clement, V., Giraudon, G., Houzelle, S., and Sandakly, F. (1993). Interpretation of remotely sensed images in a context of multisensor fusion using a multispecialist architecture. IEEE Transactions on Geoscience and Remote Sensing, 31(4):779-791. [Collins and Beveridge, 1993] Collins, R. and Beveridge, J. (1993). Matching perspective views of coplanar structures using projective unwarping and similarity matching. In Proc.Int.Conf. of Computer Vision and Pattern Recognition, CVPR, pages 240-245. [Draper et al., 1993] Draper, B. A., Hanson, A. R., and Riseman, E. M. (1993). Learning blackboard-based scheduling algorithms for computer vision. International Journal on Pattern Recognition and Artificial Intelligence, 7(2):309-328. [Flusser and Suk, 1994] Flusser, J. and Suk, T. (1994). A moment-based approach to registration of images with affine geometric distortions. IEEE Transactions on Geoscience and Remote Sensing, 32(2):382-387. [Grimson et al., 1994] Grimson, W., Huttenlocher, D., and Jacobs, D. (1994). A study of affine matching with bounded sensor error. International Journal of Computer Vision, 13(1):7-32. [Huang and Stockman, 1993] Huang, Q., and Stockman, G. (1993). Generalized tube model: Recognizing 3D elongated objects from 2D intensity images. In Proceedings CVPR, pages 104-109. [Lowe, 1987] Lowe, D.G. (1987). Three-Dimensional Object Recognition from Single Two-Dimensional Images. Artificial Intelligence, 31:355-395. Page 630 [Luo and Kay, 1992] Luo, R. and Kay, M. (1992). Data fusion and sensor integration: State-of-the-art 1990s. In Abidi, M. and Gonzalez, R., editors, Data Fusion in Robotics and Machine Intelligence, chapter~2, pages 7-135. Academic Press. [Maître, 1995] Maître, H. (1995). Image fusion and decision in a context of multisource images. In Borgefors, G., editor, Proceedings of the 9thSCIA, Scandinavian Conference on Image Analysis, volume I, pages 139-153. [Meer et al., 1990] Meer, P., Mintz, D., Montanvert, A., and Rosenfeld, A. (1990). Consensus vision. In Proceedings of the AAAI-90 Workshop on Qualitative Vision, pages 111-115. [Pinz, 1994] Pinz, A. (1994). Bildverstehen. Springers Lehrbuecher der Informatik. Springer. [Pinz and Bartl, 1992a] Pinz, A. and Bartl, R. (1992a). Information fusion in image understanding. In Proceedings of the 11.ICPR, volume I, pages 366-370. IEEE Computer Society. [Pinz and Bartl, 1992b] Pinz, A. and Bartl, R. (1992b). Information fusion in image understanding: Landsat classification and ocular fundus images. In SPIE Sensor Fusion V, Boston 92, volume 1828, pages 276-287. SPIE.
[Pinz et al., 1995a]
Pinz, A., Ganster, H., Prantl, M., and Datlinger, P. (1995a).
Mapping the retina by information fusion of multiple medical datasets.
In Human Vision, Visual Processing, and Digital Display VI,
volume 2411 of IS [Pinz et al., 1995b] Pinz, A., Prantl, M., and Datlinger, P. (1995b). Mapping the human retina. In Proceedings 9th SCIA, Scandinavian Conference on Image Analysis, Uppsala. in print. [Press et al., 1992] Press, W., Teukolsky, S., Vetterling, W., and Flannery, B. (1992). Numerical Recipes in C. Cambridge University Press, 2nd edition. [Rucklidge, 1995] Rucklidge, W. (1995). Locating objects using the hausdorff distance. In Proc. 5.ICCV, International Conference on Computer Vision, pages 457-464. [Toet, 1989] Toet, A. (1989). Image fusion by a ratio of low-pass pyramid. Pattern Recognition Letters, 9:245-253. [Webb et al., 1987] Webb, R., Hughes, G., and Delori, F. (1987). Confocal scanning laser ophthalmoscope. Appl Opt, 26:1492-1499. [Zabih and Woodfill, 1994] Zabih, R. and Woodfill, J. (1994). Non-parametric local transforms for computing visual correspondence In Eklundh, J.-O., editor, Computer Vision - ECCV'94, volume 801 of LNCS, pages 151-158. Springer. Page 631
|
|||||||||||||||||
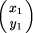 and
and 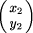 denoting locations in image 1 and image 2, respectively. A general affine transformation is defined by six independent parameters (a...f). However, a special case of the general affine transformation, the conformal transformation with four affine parameters is often sufficient for the given application, or the general affine problem can be converted
to a conformal one [
denoting locations in image 1 and image 2, respectively. A general affine transformation is defined by six independent parameters (a...f). However, a special case of the general affine transformation, the conformal transformation with four affine parameters is often sufficient for the given application, or the general affine problem can be converted
to a conformal one [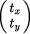 , a rotation angle
, a rotation angle 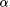 , and a scaling factor s.
, and a scaling factor s.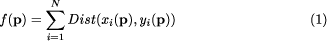
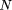 being the number of sample points,
being the number of sample points, 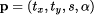 the parameter vector for the conformal transformation and
the parameter vector for the conformal transformation and 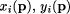 the coordinates of
the transformed sample points. Dist (
the coordinates of
the transformed sample points. Dist (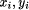 ) denotes the pixel value
at position (
) denotes the pixel value
at position (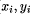 ) of the distance image.
) of the distance image.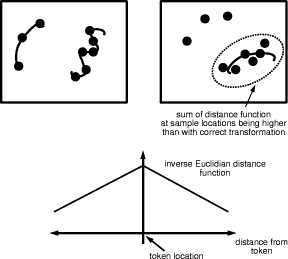
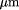 ) channels of a Landsat TM image and a digitized
MKF6 image captured during the Russian AUSTROMIR mission. A land use
classification of these images was performed. We concentrate on the
forest regions represented as tokensets shown by
Fig. 14. As in the 'shapes' example described above, we use
the borders of the forest regions for affine matching. The original
images as well as the land use classifications were supplied by the
University for Bodenkultur and are described in more detail in
[
) channels of a Landsat TM image and a digitized
MKF6 image captured during the Russian AUSTROMIR mission. A land use
classification of these images was performed. We concentrate on the
forest regions represented as tokensets shown by
Fig. 14. As in the 'shapes' example described above, we use
the borders of the forest regions for affine matching. The original
images as well as the land use classifications were supplied by the
University for Bodenkultur and are described in more detail in
[
 T/SPIE Proceedings.
in print.
T/SPIE Proceedings.
in print.