| Submission Procedure |
On Formally Correct Implementation of IEEE Computer Arithmetic
(Bulgarian Academy of Science, Bulgaria epopova@bgearn.acad.bg) Abstract: IEEE floating-point arithmetic standards 754 and 854 reflect the present state of the art in designing and implementing floating-point arithmetic units. A formalism applied to a standard non-trapping mode floating-point system shows incorrectness of some numeric and non-numeric results. A software emulation of decimal floating-point computer arithmetic supporting an enhanced set of exception symbols is reported. Some implementation details, discussion of some open questions about utility and consistency of the implemented arithmetic with the IEEE Standards are provided. The potential benefit for computations with infinite symbolic elements is outlined. Key Words: computer arithmetic, implementation, IEEE standards, exception handling Category: G.1.0 1 Introduction
At the beginning of the computer age arithmetic was defined and implemented by computer manufacturers. The main interest at that time was to optimize the speed of the operations and minimize the circuitry needed to implement them. Accuracy was only considered as a side effect. Numerical scientists suffered from these deficiencies and had to spend much effort to overcome the difficulties. Furthermore many existing floating-point units exhibit machine-dependent irregularities in behaviour which complicate the problem of writing floating-point programs that are portable, in the sense of offering equivalent numerical behaviour on different machines. Upcoming in the early eighties, the IEEE arithmetic standard 754 [ANSI/IEEE 1985], further generalized by the IEEE Std. 854 [ANSI/IEEE 1987] to remove the dependencies on radix and wordlength, changed the situation. The IEEE standards provide direct support of: - uniform floating-point formats including constrains on parameters defining values of basic and extended floating-point numbers, - well-defined computer arithmetic operations performed with maximum accuracy, - four different rounding modes including directed roundings, - execution-time diagnostics of anomalies and smoother handling of exceptions. The IEEE arithmetic standards enhance the capabilities and safety available to programmers and facilitate the movement of programs between the diverse computers adhering these standards. Between the main achievements of the standards is the provision of arithmetic operations with directed roundings Page 560 which allows implementation of numerical algorithms with automatic result verification (see e. g. [Kaucher et al. 1992], [Kulisch and Miranker 1983] for such algorithms). The IEEE standard has been widely adopted to most hardware platforms (chips: Intel 8087, Motorola 6839, etc.) and software implementations ([Falco Korn et al. 1992], [Klatte et al. 1992], [Klatte et al. 1993], [Metzger and Walter 1990], etc.). So the IEEE floating-point arithmetic, as in- tended, is rapidly becoming a de facto computer industry standard for the design of floating-point arithmetic units. The IEEE standards reflect the present state of the art and they are subject to comments, revision, reaffirmation or change. A surprising number of details and variety of different reasons for their selection must be settled in the design of a practical floating-point unit. Any proposal concerning the Standard should be judged by its consistency, utility and ease of implementation. Amongst the other comments on the standards Lynch and Swartzlander [Lynch and Swartzlander 1992] applied a formalism for specifying the num ber systems to the IEEE Std. 754 and showed that the standard conforming systems exhibit an inconsistency. Having the opportunity to develop a soft ware emulation of decimal floating-point arithmetic according to IEEE Std. 854 [ANSI/IEEE 1987], which was intended to replace the binary arithmetic in the programming language PASCAL-XSC [Klatte et al. 1992], we designed and im plemented another version of the decimal arithmetic routines which support an enhanced set of exception symbols as proposed in [Lynch and Swartzlander 1992]. Section [2 IEEE Standard and its error algebra] outlines the formalization of the IEEE non-trapping floating-point system considered in [Lynch and Swartzlander 1992] and the proposed modified system. In [Section 3] we report some implementation details and discuss the cost and the consistency with the IEEE floating-point Standards of this implementation. All considerations below are valid for both standards 754 and 854, so we shall not refer to the standard number except whenever it is especially necessary. 2 IEEE Standard and its Error Algebra
The IEEE floating-point scheme uses its formats to represent valid floating-point numbers (normalized or denormalized), called also representable numbers; some specially distinguished values as zero and infinity; and a set of special values called NaNs (Not a Number). A formalism considered in [Lynch and Swartzlander 1992] attaches a logical proposition to each element in the operation domain which defines its meaning and specifies the accuracy of the numeric results and the scope of symbolic results. In accordance with the supported floating-point formats the real numbers can be divided into six categories: (1) zero; (2) numbers too small to represent, called underflow numbers; (3) numbers which are too small to be approximated in the normalized format, called denormalized numbers; (4) numbers which may be approximated in the normalized format, called normal numbers; (5) numbers which are too large to represent, called overflow numbers; and (6) infinity. An input real value or the exact result of a floating-point arithmetic operation are approximated by some floating-point number in the supported format. Addition, multiplication and division are defined to include operation on numeric, non-numeric or mixed Page 561 operands. Four rounding modes corresponding to different type of approximation are supplied by the Standard: rounding to the nearest representable floating- point number as a default mode, rounding to zero, to minus infinity and to plus infinity. A number of exceptional situations such as Invalid Operation, Overflow, Underflow, Division by Zero and Inexact Result may arise during numerical computations in a floating-point environment conforming IEEE standards. Every exception, when it occurs must raise a flag that a program may subsequently sense and/or take a trap engineered to pass control to some code to handle the detected exceptional condition. The set of special values called NaNs are used for communicating results of Invalid Operation exceptions, attempt to extract the square root of a negative number etc. There are two types of NaNs: quiet NaN which propagate through the arithmetic operations without precipitating exceptions and signaling NaN which precipitate an Invalid Operation exception whenever an attempt is made to use one as arithmetic operand. The IEEE standards require that the default response to the exceptional situations is not to trap on them, but to compute and deliver to the destination a default result, specified in a reasonable way if not universally acceptable, for each possible exception. [Tab. 1] gives the error algebra defined by the IEEE standard for calculations performed in non-trapping mode and positive sign of the operands (valid floating-point numbers are denoted by R). 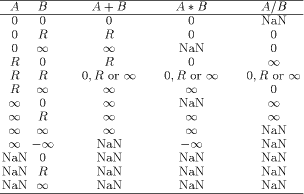 Table 1: The IEEE Std Non-, Trapping Mode Substitutions. As it was mentioned above a standard conforming computer can represent the fact that a result is indeterminate or not real with the symbol NaN. But there is no representation for prerounded results known to be in the underflow region (category 2) or the overflow region (category 5). By the following example Lynch and Swartzlander [Lynch and Swartzlander 1992] showed that the IEEE standard conforming system exhibits an inconsistency. [Fig. 1] shows an example program, the theoretically correct and the computed result in the default rounding mode. Page 562
Figure 1: Example Program, its Theoretical and Computer Execution. (LNN stands for the largest normalized number) Execution of this example is according to the rules of IEEE Standard. Each result satisfies the statement of the Standard "every operation is performed as if it first produced an intermediate result correct to infinite precision and with unbounded range and then rounded accordingly". But incorrect results are evident in lines 3 and 5. In line 3 the IEEE result is infinity, which corresponds to the proposition "the rounded theoretically correct value is greater than the maximum representable, LNN", although the theoretically correct result is 2. In line 5 the standard result is -2, but the theoretically correct result is infinity. This result is especially dangerous, because it appears to be reasonable. In [Lynch and Swartzlander 1992] the following enhanced set of elements is proposed to be used in IEEE floating-point computations to circumvent the difficulties arising in the above example: INF: the theoretically correct
value is infinite
OV: the theoretically correct
value is greater than the
maximum representable
The repeated calculations of the example based on this alternative set of exception symbols and the corresponding rules [Lynch and Swartzlander 1992] give IND.ET as the most specific correct result (B = OV, C = INDET since an OV divided by LNN may be an OV or normal number). The point is how to implement a floating-point arithmetic system in order to take the advantage of the above enhanced set of exception symbols. 3 Implementation and Consistency
An unfortunate weakness of the Standard is that so far no common programming language neither allows access to the IEEE floating-point operations with directed roundings nor provide suitable interface for testing and handling the exceptions. Only a few prototype languages [Falco Korn et al. 1992], [Klatte et al. 1992], [Klatte et al. 1993], [Metzger and Walter 1990] provide software emulatedfloating- point arithmetic conforming IEEE Std 754. For the developed floating-point arithmetic supporting an enhanced set of exception symbols the compliance with the PASCAL-XSC design is determined by the use of the following language features: Page 563 - Both PASCAL-XSC compiler [Alendoerfer and Shiriaev 1992] and the runtime system [Cordes 1991] are written in ANSI C, which ensures running PASCAL-XSC on nearly every computer. - The runtime routines simulate the decimal IEEE "double" format and the IEEE operations in software and, thus, are independent of the actually used hardware and the floating-point formats of the C compiler in use. - The PASCAL-XSC runtime system provides a set of routines which allow a flexible monitoring and handling of the exceptions. An individual condition code and a default exception routine is defined for each exception. An unique interface is given by the trap handler for all exception routines. The IEEE Standard require for each format
representation of "at least one signaling
NaN" and "at least one quiet NaN". The Standard "does not
specify the... interpretation of the sign and
significand fields of NaNs".
Representation of a decimal IEEE "double"
format number r is given on [Fig. 2]
[Bohlender et al. 1991]. According to this
representation  Figure 2: Representation of a double precision decimal number In [Tab. 2] we give the detailed non-trapping mode substitutions for addition according to the sign of the operands and according to the rounding modes. The Standard does not interpret the sign of a NaN but says that "an implementation may find it helpful to provide additional information about a variable that is a NaN through an algebraic sign". For the realization of a correct addition operation involving UN or/and OV arguments their signs have to be properly determined. So the rules of the Standard concerning the algebraic sign of a result Page 564 have to be applied even when operands or results are zero, infinite, UN or OV. The signs of the other NaNs remain not interpretable.  Figure 3: Structure of a quiet NaN 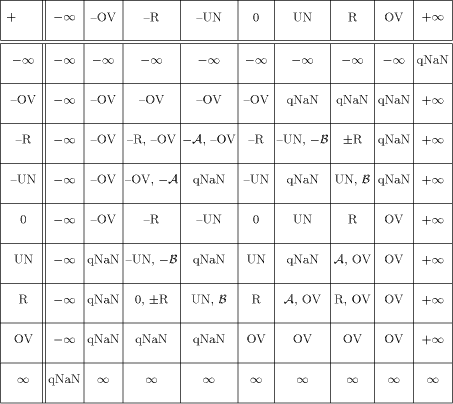 Table 2: Non-Trapping Mode Substitutions
for Addition where The following Proposition shows that a valid floating-point number results an addition/subtraction operation on any representable number and an underflow value in any rounding mode. Page 565 Proposition
For any nonzero normal or subnormal number R of the
supported floating-point format and a
positive underflow value UN, Proof follows from the inequalities 0 < UN < ulp(R) valid for any positive representable number R. A result R+ ulp(R) will signal an overflow floating-point exception when R is the largest normal number and a result R - ulp(R) will signal an Underflow floating-point exception when R is the smallest denormalized number of the supported floating-point format. [Tab. 3] and [Tab. 4] give the non-trapping mode substitutions for multiplication and division operations of positive operands. For negative or mixed sign operands the corresponding IEEE Standard rules for the algebraic sign of the result have to be additionally applied. 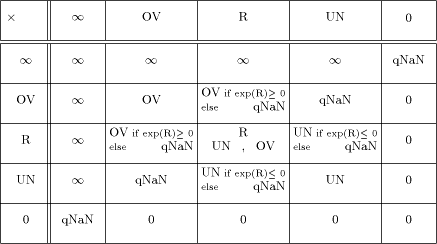 Table 3: Non-Trapping Mode Substitutions for Multiplication All operations involving UN or OV argument will signal no exceptions, except for the special cases of addition mentioned above after the Proposition. Trapped overflow on decimal string to floating-point conversion when the result lies too far outside the range of the exponent to be adjusted will deliver to the trap handler an appropriately signed OV. Similar rule is applied to the trapped underflow. In order to preserve the main purpose of the directed roundings to provide an enclosure of the theoretically correct result we have implemented the non- trapping substitutions given in [Tab. 2]-[Tab. 4] only for the arithmetic operations in round to nearest mode. The enhanced exception set requires the following modification of the IEEE definition of default result on Overflow/Underflow. Round to nearest carries all overflows to OV with the sign of the intermediate result. The delivered default result in round to nearest mode when Underflow have been detected and the corresponding trap is not enabled shall be UN with Page 566 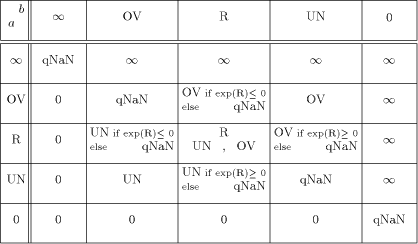 Table 4: Non-Trapping Mode Substitutions for Division the sign of the intermediate result. Remarkably, the proposed implementation scheme for a floating-point arithmetic supporting an enhanced set of exception symbols fits quite well in the frames prescribed by the IEEE floating-point Standard. This is ensured by the decision UN and OV elements to be implemented as belonging to the set of quiet NaNs and except for the substitutions from [Tab. 2]-[Tab. 4] to apply the corresponding rules for quiet NaNs prescribed by the Standard. Non-trapping substitutions from [Tab. 2]-[Tab. 4] do not contradict the Standard. Some minor inconsistencies of no practical importance can be met. The new implementation does not conform the IEEE requirement "Every operation involving one or two input NaNs, none of them signaling, shall signal no exception but, if a floating- point result is to be delivered, shall deliver as its result a quiet NaN, which should be one ofthe inputs NaNs". For example,
R/UN = neither OV nor qNaN is "one ofthe input NaNs" (UN). According to the substitution tables the result of the example of [Fig. 1] will be qNaN and the execution of line 3: C = OV/LNN = qNaN will show the same inconsistency. It should be mentioned that the difficulties connected with overflowed results in IEEE non-trapping mode computations, as those of the example of [Fig. 1], can be overcomed also at an user level by the following substitutions: 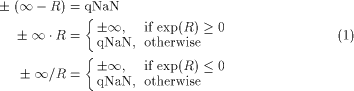 In order to ensure correct behaviour of the non-trapping floating-point computations, always when Overflow exception arises one can switch to predefined Page 567 arithmetic operations which will check for the special cases (1) and will provide more correct results. This can be done for all rounding modes. Ofcourse, checking special cases (1) will be much more time consuming than using a floating-point arithmetic supporting the enhanced exception set. The major advantage of the enhanced set of exception symbols proposed in [Lynch and Swartzlander 1992] concerns those applications dealing with infinite input elements. According to the proposed substitutions infinity as a result of a floating-point operation can be obtained only when at least one of the operands is infinity or when a nonzero number is divided by zero. Thus infinite large or infinite small in magnitude values obtained as a result of roundoff errors can be clearly distinguished from the operations involving infinities. Thus the implemented floating-point system provides more functionality and safety for only a small additional implementation cost. 4 Conclusion
A considerable amount of manpower is required for the practical implementation of any proposal concerning IEEE floating-point arithmetic. The presented implementation of floating-point arithmetic supporting an enhanced set of exception symbols comes to answer some open questions about its utility and consistency with the IEEE floating-point Standards. The new expanded computational capability is gained at no additional cost. This implementation does not implicate performance penalty. Moreover, with the enhanced capability, the computer can be used to appraise the quality and the reliability of the computed results over a wide range of applications. Acknowledgements This work was made possible due to the contract "Decimal Arithmetic" between the Bulgarian Academy of Sciences and the University of Karlsruhe, Germany. References
[Alendoerfer and Shiriaev 1992] Alendoerfer, U., Shiriaev, D.: "PASCAL-XSC to C, A Portable PASCAL-XSC Compiler"; In [Kaucher et al. 1992], 91-104. [ANSI/IEEE 1985] American National Standards Institute/Institute of Electrical and Electronics Engineers: "IEEE Standard for Binary Floating-Point Arith- metic"; ANSI/IEEE Std 754-1985, New York (1985). [ANSI/IEEE 1987] American National Standards Institute/Institute of Electrical and Electronics Engineers: "IEEE Standard for Radix-lndependent Floating- Point Arithmetic"; ANSI/IEEE Std 854-1987, New York (1987). [Bohlender et al. 1991] Bohlender, G., Cordes, D., Klatte, R., Kraemer, W.: "Technical Specifications for a Decimal Arithmetic"; lnstitut fuer Angewandte Mathematik, Universitaet Karlsruhe, Karlsruhe (1991). [Cordes 1991] Cordes, D.: "Runtime System for a PASCAL-SC Compiler"; In [Kaucher et al. 1992], 151-160. [Falco Korn et al. 1992] Falco Korn, C., Gutzwiller, S., Koenig, S., Ullrich, Ch.: "Modula-SC. Motivation, Language Definition and lmplementation"; ln [Kaucher et al. 1992], 161-181.
Page 568 [Kaucher et al. 1992] Kaucher, E.,Markov, S. M.,Mayer, G. (Eds.): "Computer Arithmetic, Scientific Computation and Mathematical Modelling"; IMACS Annals on Computing and Appl. Math., 12, J. C. Balzer, Basel (1992). [Klatte et al. 1993] Klatte, R., Kulisch, U., Lawo, C., Rauch, M., Wiethoff, A.: "CXSC A C++ Class Library for Extended Scientific Computation"; Springer, Berlin (1993). [Klatte et al. 1992] Klatte, R., Kulisch, U., Neaga, M., Ratz, D., Ullrich, Ch.: "PASCAL-XSC Language Reference with Examples"; Springer, Berlin (1992). [Kulisch and Miranker 1981] Kulisch, U., Miranker, W. L.: "Computer Arithmetic in Theory and Practice"; Academic Press, New York (1981). [Kulisch and Miranker 1983] Kulisch, U., Miranker, W. L. (Eds.): "A New Approach to Scientific Computation"; Academic Press, New York (1983). [Lynch and Swartzlander 1992] Lynch, T. W., Swartzlander E. E.: "A Formalization for Computer Arithmetic"; In Atanassova, L., Herzberger, J. (Eds.): "Computer Arithmetic and Enclosure Methods" Elsevier Sci. Publishers B. V. (1992), 137-145. [Metzger and Walter 1990] Metzger, M., Walter, W. V.: "FORTRAN-SC: A Programming Language for Engineering/Scientific Computation" In Ullrich, Ch. (Ed.): "Contribution to Computer Arithmetic and Self-Validating Numerical Methods"; IMACS Annals on Computing and Appl. Math., 7, J. C. Balzer, Basel (1990), 427-441.
Page 569
|
|||||||||||||||||
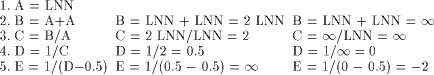
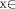 representables: the theoretically correct
value is approximately x
UN: the theoretically correct
result is smaller than the
minimum representable
0: the theoretically correct
result is zero
INDET: the theoretically correct
result is indeterminable.
representables: the theoretically correct
value is approximately x
UN: the theoretically correct
result is smaller than the
minimum representable
0: the theoretically correct
result is zero
INDET: the theoretically correct
result is indeterminable.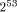 - 2 encodings are used
for the NaNs. By default the PASCAL-XSC runtime system
assumes that
a signaling NaN is identified by bit 51 of
this representation being set. A quiet NaN
is identified by bit 51 of the representation of the floating-point
number being not set. We take advantage of
the freedom given by the Standard and use
part of the encodings of the quiet NaNs for
the representation of the additional
exception symbols UN and OV. The INDET
value is carried by the qNaN itself. Thus
the structure of a quiet NaN in the corresponding floating-point
system supporting the extended set of
exception symbols becomes as that presented on
[Fig. 3]. To be more specific an INDET
value is represented by d = 7, OV by d = 3
and UN by d = 1 [see Fig. 2].
- 2 encodings are used
for the NaNs. By default the PASCAL-XSC runtime system
assumes that
a signaling NaN is identified by bit 51 of
this representation being set. A quiet NaN
is identified by bit 51 of the representation of the floating-point
number being not set. We take advantage of
the freedom given by the Standard and use
part of the encodings of the quiet NaNs for
the representation of the additional
exception symbols UN and OV. The INDET
value is carried by the qNaN itself. Thus
the structure of a quiet NaN in the corresponding floating-point
system supporting the extended set of
exception symbols becomes as that presented on
[Fig. 3]. To be more specific an INDET
value is represented by d = 7, OV by d = 3
and UN by d = 1 [see Fig. 2].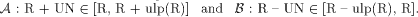
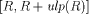 is the smallest machine interval containing
R + UN and
is the smallest machine interval containing
R + UN and 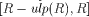 is the smallest
machine interval containing R - UN.
is the smallest
machine interval containing R - UN.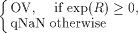 and
and