| Submission Procedure |
Modular Range Reduction: A New Algorithm for Fast and Accurate Computation of the Elementary Functions
(Lab. LIP, Ecole Normale Superieure de Lyon Marc.Daumas@lip.ens-lyon.fr) (Lab. LIP, Ecole Normale Superieure de Lyon Christophe.Mazenc@lip.ens-lyon.fr) (Lab. LIP, Ecole Normale Superieure de Lyon Xavier.Merrheim@lip.ens-lyon.fr) (CNRS, Lab. LIP, Ecole Normale Superieure de Lyon Jean-Michel.Muller@lip.ens-lyon.fr) Abstract: A new range reduction algorithm, called Modular
Range Reduction (MRR), briefly introduced by the authors in [Daumas
et al. 1994] is deeply analyzed. It is used to reduce the arguments
to exponential and trigonometric function algorithms to be within the
small range for which the algorithms are valid. MRR reduces the
arguments quickly and accurately. A fast hardwired implementation of
MRR operates in time Key Words: Computer Arithmetic, Elementary Functions, Range Reduction 1 Introduction
The algorithms used for evaluating the elementary functions (polynomial or rational approximations [Cody and Waite 1980], [Remes 1934], Taylor expansions, shift-and-add algorithms-see [Ercegovac 1973], [DeLugish 1970], [Walther 1971] and [Asada et al. 1987], table lookup methods...) only give a correct result if the argument is within a given bounded interval. In order to evaluate an elementary function f(x) for any x, one must find some 'transformation' that makes it possible to deduce f(x) from some value g(x*), with: -x* is deduced from x, x* is called the reduced argument -x* belongs to the convergence domain of the algorithm implemented for the evaluation of g. In practice, there are two different kinds of reduction: 1. Additive reduction. x* is equal to x - kC, where k is an integer
and C a constant (for instance, for the trigonometric functions, C is a multiple of Page 162 2. Multiplicative reduction. x* is equal to Example 1 Computation of the cosine function. Assume that we want to
evaluate cos(x), and that the convergence domain of the algorithm
used to evaluate the sine and cosine of the reduced argument contains
The previous reduction mechanism is an additive reduction. Let us examine another example of additive reduction. Example 2 Computation of the exponential function. Assume that we
want to evaluate
The radix-2 number system makes the final multiplication by Another way of performing the range reduction for the exponential
function (with an algorithm whose convergence domain is - we will be able to compute x* very accurately, - the required convergence interval is smaller, which means that to reach the same accuracy, we need a smaller number of coefficients for a polynomial or rational approximation, - there will not be any error when deducing Anyway, range reduction is more a problem for trigonometric functions than for exponentials, since, in practice, we never have to deal with exponentials of very large numbers: they merely are overflows! Page 163 Example 3 Computation of the logarithm function. Assume that we want
to evaluate ln(x), x > 0, in a radix-2 number system, and that the
convergence domain of the algorithm used to compute the logarithm of
the reduced argument contains - Compute - Compute g(x*, k) = ln(x*) - Compute ln(x) = g(x*,k) + k ln(2) The previous mechanism is a multiplicative reduction. In practice, multiplicative reduction is not a problem: when
computing the usual mathematical functions, it only occurs with
logarithms and n-th roots. With these functions, as in the example
above, C can be chosen equal to a power of the radix of the number
system. This makes the computation of 2 The Modular Range Reduction Algorithm
We focus on the following problem: we assume that we have an
algorithm able to compute the function g in an interval x* = x - kC (2) If
Table 1. The different cases in additive range-reduction Page 164 It is worth noticing that: 1. In some practical cases, it is not necessary to fully compute k.
For instance, for the trigonometric functions, if C = 2. With the usual algorithms for evaluating the elementary functions, one can assume that the length of the convergence domain Let us define - Computing k = - Computing the reduced argument x* = x - kC by the means of a multiplication by k or a table-lookup if the values kC are pre computed and stored followed by a subtraction. The above process may be rather inaccurate (for large values of x, the final subtraction step leads to a catastrophic cancellation - although cunning tricks have been proposed to limit this cancellation [Cody and Waite 1980]). In [Daumas et al. 1994] we briefly proposed a new algorithm, called the modular reduction algorithm (MRR), that performs the range reduction quickly and accurately. In the following we deeply analyze that algorithm in terms of speed and accuracy, and we propose architectures implementing it. 2.1 Fixed-point reduction
First of all, we assume that the input operands are Fixed-point
radix-2 numbers, less than
represents the number We assume that we should perform a redundant range reduction, and we
call Page 165 First reduction We compute the number1*: 1*(This formula looks correct only for positive values of
Since the
has an absolute value less than Second reduction Define the
where Let us define
Proof
Since k can be deduced from During this reduction process, we perform the addition
of Page 166
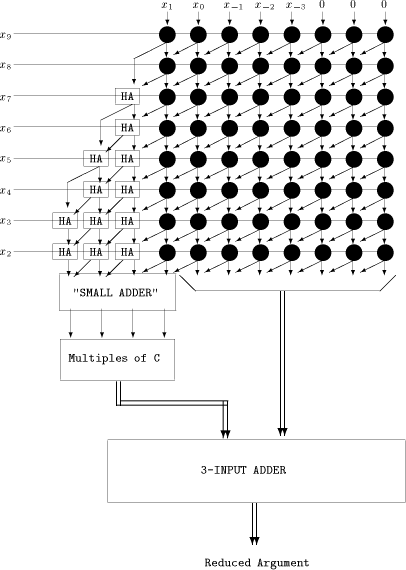
Fig. 1. The Modular Reduction Algorithm Example 4. Assume we need to compute sines of angles between - N = 20 and - The first range reduction consists of the addition of 19 terms - Page 167 - To obtain the reduced argument with p significant fractional bits, one needs to store the Assume we compute the sine of 355. The binary representation of 355 is
101100011. Therefore during the first reduction, we have to compute
We get 2.2 Floating-point reduction
Now, assume that the input value x is a radix-2 floating-point number:
The range reduction can be performed exactly as in the fixed-point
case. During the first reduction, we replace the addition of the
terms 3 Architectures for Modular Reduction
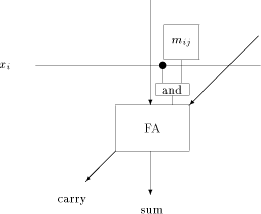
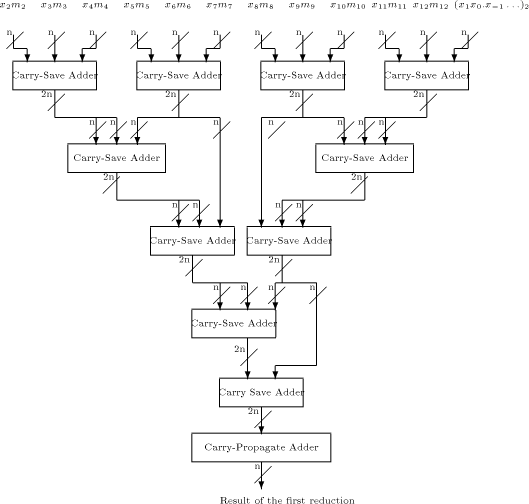
The first reduction consists of adding Page 168 Wallace
tree [Wallace 1964]. In Fig. 3, The similarity between the range reduction and the multiplication leads us to another idea: in order to accelerate the first reduction, one can perform a Booth recoding [Booth 1951], or merely a modified booth recoding [Hwang 1979], of x. This would give a signed digit (with digits -1, 0 and 1) representation of x with at least half of the digits equal to zero. Then the number of terms to be added during the first reduction would be halved. 4 Accuracy of MRR with Floating-point Inputs
As pointed out in section 2.2, if the input value x is a m-mantissa
bit radix-2 floating-point number, and if the terms 4.1 How could MRR Results close to Zero be avoided ?
As in section 2.2, the input number x is the radix-2 floating-point number:
M is an integer. Assume that the result of the range reduction is very small, say less than a very small real number
This implies:
This means that
Page 169 Let us define
Since (from the theory of continued fractions), for each rational
number
So, if one wants to get a relative error
5 Conclusion
We have proposed a fast and accurate algorithm to perform the range
reduction for computing the elementary functions. This algorithm can
be implemented using a slightly modified multiplier, so that range
reduction and multiplication can be performed using the same
hardware, which can save some silicon area on a circuit. Using this
algorithm, accurately and quickly computing the sine of a number such
as Page 170
Fig. 2. A cellular array for range reduction Page 171
Fig. 3. A black cell of the cellular array Page 172
Fig. 4. A logarithmic-time range-reduction tree Page 173 References
[Asada et al. 1987] T. Asada, N. Takagi, and S. Yajima. A hardware algorithm for computing sine and cosine using redundant binary representation. Systems and computers in Japan, 18(8), 1987. [Booth 1951] A.D. Booth. A signed binary multiplication technique. Quarterly journal of mechanics and applied mathematics, 4(2):236-240, 1951. Reprinted in E.E. Swartzlander, Computer Arithmetic, Vol. 1, IEEE Computer Society Press Tutorial, 1990. [Braun 1963] E.L. Braun. Digital computer design. New York academic, 1963. [Cody and Waite 1980] W. Cody and W. Waite. Software Manual for the Elementary Functions. Prentice-Hall Inc, 1980. [Dadda 1965] L. Dadda. Some schemes for parallel multipliers. Alta Frequenza, 34:349-356, March 1965. Reprinted in E.E. Swartzlander, Computer Arithmetic, Vol. 1, IEEE Computer Society Press Tutorial, 1990. [Daumas et al. 1994] M. Daumas, C. Mazenc, X. Merrheim, and J.M. Muller. Fast and Accurate Range Reduction for the Computation of Elementary Functions. In 14th IMACS World Congress on Computational and Applied Mathematics, Atlanta, Georgia, 1994. [Ercegovac 1973] M.D. Ercegovac. Radix 16 evaluation of certain elementary functions. IEEE Transactions on Computers, C-22(6), June 1973. Reprinted in E.E. Swartzlander, Computer Arithmetic, Vol. 1, IEEE Computer Society Press Tutorial, 1990. [Harata et al. 1987] Y. Harata, Y. Nakamura, H. Nagase, M. Takigawa, and N.,l,akagi. A high-speed multiplier using a redundant binary adder tree. IEEE journal of solid-state circuits, SC-22(1):28-34, February 1987. Reprinted in E.E. Swartzlander, Computer Arithmetic, Vol. 2, IEEE Computer Society Press Tutorial, 1990. [Hwang 1979] K. Hwang. Computer Arithmetic Principles, Architecture and design. Wiley & Sons Inc, 1979. [DeLugish 1970] B. De Lugish. A Class of Algorithms for Automatic Evaluation of Functions and Computations in a Digital Computer. PhD thesis, Dept. of Computer Science, University of Illinois, Urbana, 1970. [Nakamura 1986] S. Nakamura. Algorithms for iterative array multiplication. IEEE Transactions on Computers, C-35(8), August 1986. [Remes 1934] E. Remes. Sur un procede convergent d,approximations successives pour determiner les polynomes d'approximation. C.R. Acad. Sci. Paris, 198, 1934. [Takagi et al. 1985] N. Takagi, H. Yasukura, and S. Yajima. High speed multiplication algorithm with a redundant binary addition tree. IEEE Transactions on Computers, C-34(9), September 1985. [Volder 1959] J. Volder. The cordic computing technique. IRE Transactions on Electronic Computers, 1959. Reprinted in E.E. Swartzlander, Computer Arithmetic, Vol. 1, IEEE Computer Society Press Tutorial, 1990. [Wallace 1964] C.S. Wallace. A suggestion for a fast multiplier. IEEE Transactions on Electronic Computers, pages 14-17, February 1964. Reprinted in E.E. Swartzlander, Computer Arithmetic, Vol. 1, IEEE Computer Society Press Tutorial, 1990. [Walther 1971] J. Walther. A unified algorithm for elementary functions. In Joint Computer Conference Proceedings, 1971. Reprinted in Page 174 E.E. Swartzlander, Computer Arithmetic, Vol. 1, IEEE Computer Society Press Tutorial, 1990. Page 175
|
|||||||||||||||||
 (log(n)), where n is the number of bits of the
binary input value. For example, with MRR it becomes possible to
compute the sine and cosine of a very large number accurately. We
propose two possible architectures implementing this algorithm.
(log(n)), where n is the number of bits of the
binary input value. For example, with MRR it becomes possible to
compute the sine and cosine of a very large number accurately. We
propose two possible architectures implementing this algorithm. 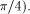
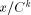 , where k is an
integer and C a constant (for instance, for the
logarithm function, a convenient choice for C is the radix of the
number system).
, where k is an
integer and C a constant (for instance, for the
logarithm function, a convenient choice for C is the radix of the
number system).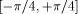 . We choose
. We choose 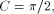 and the computation of cos(x) is
decomposed in three steps:
and the computation of cos(x) is
decomposed in three steps:
 in a radix-2 number system, and that the
convergence domain of the algorithm used to evaluate the exponential of the reduced argument contains
in a radix-2 number system, and that the
convergence domain of the algorithm used to evaluate the exponential of the reduced argument contains 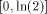 . We choose C = ln(2),
and the computation of
. We choose C = ln(2),
and the computation of 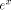 is decomposed in three steps:
is decomposed in three steps: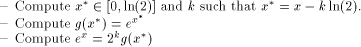
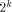 straightforward.
straightforward.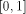 ) is to
choose
) is to
choose 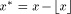 ,
,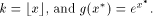 Then,
Then, 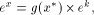 and
and 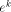 can either be evaluated by performing a few multiplications -
since k is an integer - or by table-lookup. Usually, this latter
method is preferable, since there is no loss of accuracy when
computing x*. With the range reduction algorithm we give in the
following, the former choices for x*, g, and k become interesting,
for several reasons:
can either be evaluated by performing a few multiplications -
since k is an integer - or by table-lookup. Usually, this latter
method is preferable, since there is no loss of accuracy when
computing x*. With the range reduction algorithm we give in the
following, the former choices for x*, g, and k become interesting,
for several reasons: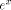 from g(x*).
from g(x*).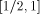 . We choose C = 2, and the
computation of ln(x)is decomposed in three steps:
. We choose C = 2, and the
computation of ln(x)is decomposed in three steps: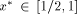 and k such that
and k such that 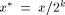 (if x is a normalized radix-2 floating-point number, x* is its mantissa, while k is its exponent).
(if x is a normalized radix-2 floating-point number, x* is its mantissa, while k is its exponent).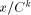 straight-forward.
Therefore, in the following, we concentrate on the problem of
additive range reduction only.
straight-forward.
Therefore, in the following, we concentrate on the problem of
additive range reduction only.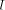 of the form
of the form 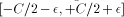 (we call this case 'symmetrical reduction')
or
(we call this case 'symmetrical reduction')
or 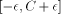 (we call this case 'positive reduction'), with
(we call this case 'positive reduction'), with 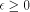 .
We want to compute
.
We want to compute 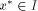 and an integer k such that:
and an integer k such that: 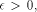 then x* and k are not uniquely defined by Eq. 2. In such a
case, the problem of deducing these values from x will be
called 'redundant range reduction'. For example, if
then x* and k are not uniquely defined by Eq. 2. In such a
case, the problem of deducing these values from x will be
called 'redundant range reduction'. For example, if 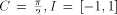 and x = 2.5, then k = 1 and x* = 0.929203 ... or k = 2 and
x* = -0.641592 ... are possible values. If
and x = 2.5, then k = 1 and x* = 0.929203 ... or k = 2 and
x* = -0.641592 ... are possible values. If 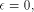 this problem is
called 'non-redundant range reduction'. As in many fields of
computer arithmetic, redundancy will allow faster algorithms. Table 1 sums-up the different possible cases.
this problem is
called 'non-redundant range reduction'. As in many fields of
computer arithmetic, redundancy will allow faster algorithms. Table 1 sums-up the different possible cases.
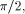 then one just needs to know k mod 4. If C =
then one just needs to know k mod 4. If C = 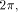 there is no need for any information about k.
there is no need for any information about k.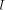 is greater than C, i.e. that we can perform a redundant range reduction. For instance, with the CORDIC algorithm, when performing rotations (see [
is greater than C, i.e. that we can perform a redundant range reduction. For instance, with the CORDIC algorithm, when performing rotations (see [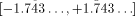 , which is much larger than
, which is much larger than 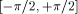 . With polynomial or rational approximations, the convergence domain can be enlarged by adding one coefficient to the approximation.
. With polynomial or rational approximations, the convergence domain can be enlarged by adding one coefficient to the approximation.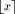 as the nearest integer to x. Usually, the range
reduction is done by:
as the nearest integer to x. Usually, the range
reduction is done by: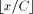 (in the case of a positive reduction), or k =
(in the case of a positive reduction), or k = 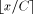 (in the case of a symmetrical reduction) by the means of multiplication or division.
(in the case of a symmetrical reduction) by the means of multiplication or division.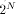 . These numbers have a N-bit integer
part and a p-bit fractional part. So the digit chain:
. These numbers have a N-bit integer
part and a p-bit fractional part. So the digit chain: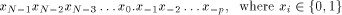
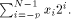
 the integer such that
the integer such that 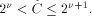 Let us define, for
Let us define, for 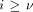 the number
the number 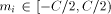
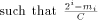 is an
integer (in the following, we will write
is an
integer (in the following, we will write 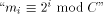 ). The
Modular Range Reduction (MRR) algorithm consists in performing the two following steps:
). The
Modular Range Reduction (MRR) algorithm consists in performing the two following steps:  . It would be more correct, although maybe less clear, to write:
. It would be more correct, although maybe less clear, to write: 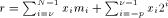 )
)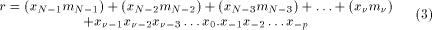
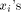 are equal to 0 or 1, this computation is reduced to
the sum of
are equal to 0 or 1, this computation is reduced to
the sum of 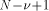 terms. The result r of this first reduction is
between
terms. The result r of this first reduction is
between 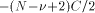
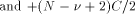 . This is a consequence of
the fact that all the
. This is a consequence of
the fact that all the 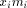 have an absolute value less than C/2 and
have an absolute value less than C/2 and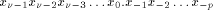
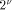 , which is less than C.
, which is less than C.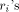 as
the digits of the result of the first reduction:
as
the digits of the result of the first reduction: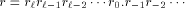
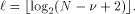
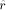 as the number obtained by truncating
the binary representation of r after the
as the number obtained by truncating
the binary representation of r after the 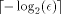 -th bit, that
is (using the relation
-th bit, that
is (using the relation 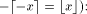
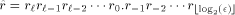
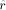 is an m-digit number, where m =
is an m-digit number, where m = 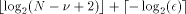 is a very small number in all practical cases (see the example
below). If we define k as
is a very small number in all practical cases (see the example
below). If we define k as 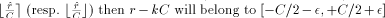
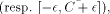 i.e. it will be the correct result of the symmetrical (resp. positive) range reduction.
i.e. it will be the correct result of the symmetrical (resp. positive) range reduction.
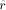 , this second reduction step will be
implemented by looking up the value kC in a
, this second reduction step will be
implemented by looking up the value kC in a 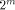 -bit entry table at the
address constituted by the bits of
-bit entry table at the
address constituted by the bits of 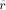 . Fig.1 Sums up the different steps of MRR.
. Fig.1 Sums up the different steps of MRR. 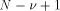 terms. If these terms (namely the
terms. If these terms (namely the 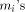 and the value kC
of the second reduction step) are represented in fixed-point with q
fractional bits (i.e. the error on each of these term is bounded by
and the value kC
of the second reduction step) are represented in fixed-point with q
fractional bits (i.e. the error on each of these term is bounded by 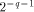 ), then the difference between the result of the computation and
the exact reduced argument is bounded by
), then the difference between the result of the computation and
the exact reduced argument is bounded by 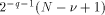 .
In order to obtain the reduced argument x* with the same absolute accuracy as
the input argument x (i.e. p significant fixed-point fractional
digits), one needs to store the
.
In order to obtain the reduced argument x* with the same absolute accuracy as
the input argument x (i.e. p significant fixed-point fractional
digits), one needs to store the 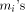 and the values kC with p +
and the values kC with p +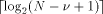 fractional bits.
fractional bits.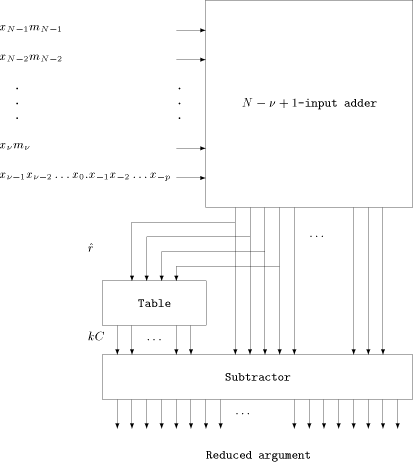
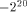 and
and 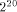 , and that the algorithm used with the reduced arguments is CORDIC
[
, and that the algorithm used with the reduced arguments is CORDIC
[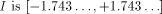 , therefore (since 1.743
, therefore (since 1.743 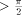 ) we have to perform a symmetrical redundant range reduction, with
) we have to perform a symmetrical redundant range reduction, with 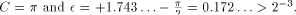 We immediately get the following parameters:
We immediately get the following parameters: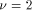
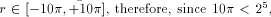 the second reduction step requires a table with
the second reduction step requires a table with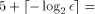 8-address bits.
8-address bits.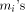 and the values kC with p + 5 bits.
and the values kC with p + 5 bits.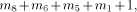 where:
where: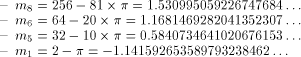
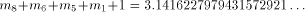 The second
reduction consists in subtracting
The second
reduction consists in subtracting  from that result, which gives
from that result, which gives 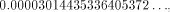 the sine of which is
the sine of which is 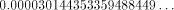 Therefore, sin(355) = -0.000030144353359488449 ...
Therefore, sin(355) = -0.000030144353359488449 ...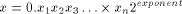
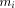 by the addition of the terms
by the addition of the terms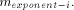 As previously,
As previously, 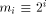 mod C is the number belonging
to
mod C is the number belonging
to 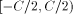 such that
such that 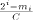 is an integer. The main difference
between this
reduction method and the other ones is that during the reduction
process, we just add numbers (the
is an integer. The main difference
between this
reduction method and the other ones is that during the reduction
process, we just add numbers (the 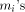 ) of the same order of
magnitude, represented in fixed-point. This makes the reduction very
accurate. One can easily show that if the
) of the same order of
magnitude, represented in fixed-point. This makes the reduction very
accurate. One can easily show that if the 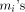 and the terms kC of
the second reduction are represented with q fractional bits then the
absolute error on the reduced argument is bounded by
and the terms kC of
the second reduction are represented with q fractional bits then the
absolute error on the reduced argument is bounded by 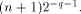 Thus, for instance it is possible to compute with good accuracy the
sine and cosine of a huge floating-point number. In floating point
number systems, one would prefer informations on the relative error:
this will be discussed later.
Thus, for instance it is possible to compute with good accuracy the
sine and cosine of a huge floating-point number. In floating point
number systems, one would prefer informations on the relative error:
this will be discussed later.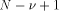 numbers. This
addition can be performed in a redundant number system (carry-save or
signed-digit) in order to benefit from the carry-free ability of such
a system, and/or in an arborescent way.
This problem is obviously
closely related to the problem of multiplying two numbers
(multiplying
numbers. This
addition can be performed in a redundant number system (carry-save or
signed-digit) in order to benefit from the carry-free ability of such
a system, and/or in an arborescent way.
This problem is obviously
closely related to the problem of multiplying two numbers
(multiplying 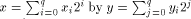 reduces to
computing the sum of the q + 1 terms
reduces to
computing the sum of the q + 1 terms 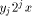 ). Therefore, almost
all the classical architectures proposed in the multiplication literature (see for instance [
). Therefore, almost
all the classical architectures proposed in the multiplication literature (see for instance [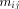 is the digit of weight
is the digit of weight 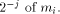 This similarity between the Modular Range Reduction algorithm and the
multiplication makes it possible to perform both operations with the same hardware, which can save some silicon area on a circuit.
This similarity between the Modular Range Reduction algorithm and the
multiplication makes it possible to perform both operations with the same hardware, which can save some silicon area on a circuit.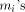 of the first
reduction and the terms kC of the second reduction are represented with q fractional bits then the absolute error on the reduced argument is bounded by
of the first
reduction and the terms kC of the second reduction are represented with q fractional bits then the absolute error on the reduced argument is bounded by 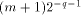 . This makes it possible to evaluate sines and cosines of huge floating-point numbers with a good absolute accuracy.
However, in floating-point, one is more concerned
with the relative accuracy: what could be done if the result of MRR
is zero or a number close to zero ? This would indicate that the exact reduced argument is very small, but the computed value would only have a few (maybe not at all)
significant digits. In the sequel of this paper, we deal with that problem.
. This makes it possible to evaluate sines and cosines of huge floating-point numbers with a good absolute accuracy.
However, in floating-point, one is more concerned
with the relative accuracy: what could be done if the result of MRR
is zero or a number close to zero ? This would indicate that the exact reduced argument is very small, but the computed value would only have a few (maybe not at all)
significant digits. In the sequel of this paper, we deal with that problem.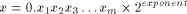
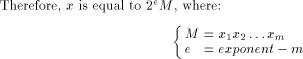
 . This means that there exists an integer k such that:
. This means that there exists an integer k such that: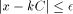

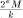 is a very good rational approximation of C.
To see to what extent relation (4) is likely to happen, we can compare this approximation to the sequence of the 'best' possible rational approximation of C, i.e. the sequence of its continued fraction
approximations. Let us call
is a very good rational approximation of C.
To see to what extent relation (4) is likely to happen, we can compare this approximation to the sequence of the 'best' possible rational approximation of C, i.e. the sequence of its continued fraction
approximations. Let us call  the sequence of the
continued fraction approximations of C. For instance if C =
the sequence of the
continued fraction approximations of C. For instance if C =  then:
then: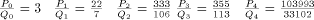
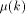 as the integer such that:
as the integer such that: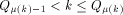
 such that
such that 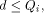 we have:
we have: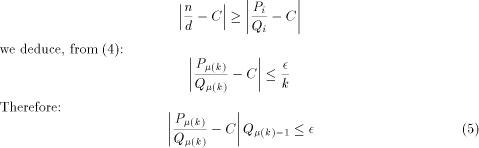
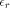 for input values lower than
for input values lower than 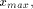 the way to proceed is the following one:
the way to proceed is the following one: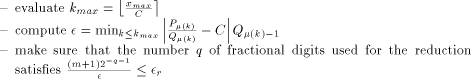
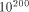 becomes possible.
becomes possible.