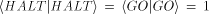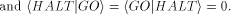Halting Probability Amplitude of Quantum Computers
K. Svozil
Institute for Theoretical Physics, Technische Universitaet Wien,
Wiedner Hauptstrasse 8-10/136, A-1040 Vienna, Austria
e-mail:svozil@tph.tuwien.ac.at
Abstract:
The classical halting
probability  introduced by Chaitin is generalized to quantum
computations. introduced by Chaitin is generalized to quantum
computations. (The quantum omega was invented in a meeting of G. Chaitin,
A. Zeilinger and the author (K. S.) in a Viennese coffee house
(Cafe Braeunerhof) in January 1991.
Thus, the group should be credited for the original invention,
whereas any blame should remain with the author.)
1 Halting Probability Amplitude of Quantum Computers
Chaitin's  [1],[2],[3] is a magic
number.
It is a measure for arbitrary programs to take a finite number of
execution steps and
then halt.
It contains the solution for all halting problems, and hence to
questions codable into halting problems, such as Fermat's theorem.
It contains the solution for the question of whether or not a particular
exponential Diophantine equation
has infinitely many or a finite number of solutions.
And, since [1],[2],[3] is a magic
number.
It is a measure for arbitrary programs to take a finite number of
execution steps and
then halt.
It contains the solution for all halting problems, and hence to
questions codable into halting problems, such as Fermat's theorem.
It contains the solution for the question of whether or not a particular
exponential Diophantine equation
has infinitely many or a finite number of solutions.
And, since  is provable 'algorithmically incompressible,' it
is Martin-Loef/Chaitin/Solovay random. Therefore, is provable 'algorithmically incompressible,' it
is Martin-Loef/Chaitin/Solovay random. Therefore,  is both: a
mathematicians 'fair coin,' and a formalist's nightmare. is both: a
mathematicians 'fair coin,' and a formalist's nightmare. Here,  is generalized to quantum computations. is generalized to quantum computations. Consider a (not necessarily universal) quantum computer C and its
ith
program 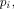 which, at time
which, at time  can be described by a quantum state
[4], [5], [6], [7], [8], [9], [10], [11], [12] can be described by a quantum state
[4], [5], [6], [7], [8], [9], [10], [11], [12] 
A typical realisation of C would be by an array of
generalized four-port beam splitters [13]. In what follows we shall assume that the program 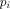 is
coded classically. That is, we choose a finite code alphabet A
and denote by A* the set of all strings over A.
Any program is
coded classically. That is, we choose a finite code alphabet A
and denote by A* the set of all strings over A.
Any program 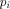 is coded as a classical sequence is coded as a classical sequence 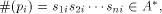 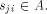 (In what follows, (In what follows, 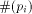 will be abbreviated by will be abbreviated by 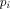 .)
We assume prefix coding
[14], [1], [15], [3]; i.e., the domain of C is
prefix-free such that no admissible program is the prefix of another
admissible program.
Furthermore, without loss of generality, we consider only empty input
strings. .)
We assume prefix coding
[14], [1], [15], [3]; i.e., the domain of C is
prefix-free such that no admissible program is the prefix of another
admissible program.
Furthermore, without loss of generality, we consider only empty input
strings. Page 201
In quantum information theory, the state 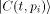 of the computer C with
program
of the computer C with
program 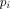 is
representable by quantum bits (qbits).
Every qbit is in a coherent superposition of the classical bit basis is
representable by quantum bits (qbits).
Every qbit is in a coherent superposition of the classical bit basis 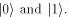 Assume that the states (1)
are orthogonal and normalized.
The computer C evolves according to a unitary
operator U such that (discrete time evolution)
Assume that the states (1)
are orthogonal and normalized.
The computer C evolves according to a unitary
operator U such that (discrete time evolution) 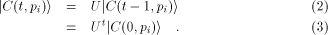
More specifically,
a quantum computer can be in a coherent superposition of the
halting and the non-halting state [6], [16] 
We shall call this quantum bit 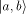 the halting bit.
The symbols the halting bit.
The symbols 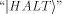 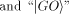 represent orthonormal vectors [17]
in the twodimensional complex
Hilbert space spanned by them.
Let the halting state
represent orthonormal vectors [17]
in the twodimensional complex
Hilbert space spanned by them.
Let the halting state 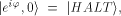 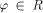 be the physical realization that the computer has
'halted;' likewise let
be the physical realization that the computer has
'halted;' likewise let 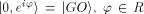 be the physical realization that the computer has not
`halted'.
Note that, since quantum computations are governed by unitary evolution
laws which are reversible, the halting state does not mean that the
computer does not change as time evolves. It just means that it has set
a signal --- the halting bit --- to indicated that it has finished its
task.
a and b are complex numbers which are a quantum mechanical measure
of the probability amplitude that the computer is in the halting and the
non-halting states, respectively.
(The corresponding probabilities are
be the physical realization that the computer has not
`halted'.
Note that, since quantum computations are governed by unitary evolution
laws which are reversible, the halting state does not mean that the
computer does not change as time evolves. It just means that it has set
a signal --- the halting bit --- to indicated that it has finished its
task.
a and b are complex numbers which are a quantum mechanical measure
of the probability amplitude that the computer is in the halting and the
non-halting states, respectively.
(The corresponding probabilities are 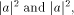 respectively.)
One
important feature of the quantum information concept ist that it does
not
merely allow two-valued states but a coherent superposition thereof. respectively.)
One
important feature of the quantum information concept ist that it does
not
merely allow two-valued states but a coherent superposition thereof. In the orthonormal halting basis
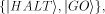 the computer C with classical input
the computer C with classical input 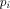 can be represented by
can be represented by 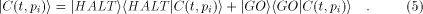
In the spirit of quantum recursion theory [16], assume
that initially,
i.e., at time t=0, the computer is prepared such that its halting bit
is in a coherent 50:50-superposition; i.e.,
in terms of the halting basis, 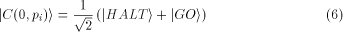
for all 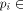 A*.
This corresponds to the fact that initially it is unknown whether or not
the computer halts on A*.
This corresponds to the fact that initially it is unknown whether or not
the computer halts on 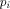 .
When during the time evolution the computer has completed its task,
the halting bit value is switched to .
When during the time evolution the computer has completed its task,
the halting bit value is switched to
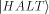 by some internal operation,
otherwise it
remains in the coherent 50:50-superposition
of equation (6).
(Alternatively, the computer could be initially prepared
in the non-halting state by some internal operation,
otherwise it
remains in the coherent 50:50-superposition
of equation (6).
(Alternatively, the computer could be initially prepared
in the non-halting state 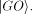 After completion of the
task, the halting bit is again
switched to
the halting state
After completion of the
task, the halting bit is again
switched to
the halting state 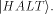 In this case, the subtractions of
In this case, the subtractions of 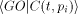 in
equations (7), (8) and (9) below would have to be eliminated.) in
equations (7), (8) and (9) below would have to be eliminated.) Page 202
In analogy to the fully classical case [1],[18],[3]
the quantum halting amplitude 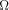 can be defined
as a weighted expectation over all computations of C with classical
input can be defined
as a weighted expectation over all computations of C with classical
input 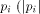 stands for the length of stands for the length of 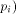 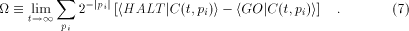
Likewise, for particular output states 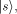 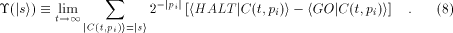
For a set of output states 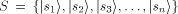 which correspond to mutually orthogonal
vectors in Hilbert space, which correspond to mutually orthogonal
vectors in Hilbert space, 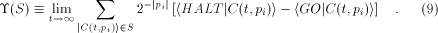
For nontrivial choices of the quantum computer C,
several remarks are in order.
(In what follows, we mention only 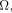 but the comments apply to but the comments apply to 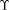 as well.) as well.) First, note that if the program is also
coded in qbits, the above sum becomes an
integral over continuously many states per code symbol of the programs.
In this case, the Kraft sum needs not converge. Second, just as for the classical analogue it is possible to 'compute' 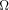 as a limit from below
by considering
in the t'th computing step (time t) all programs of length t
which have already halted.
(This 'computation' suffers
from a radius of convergence which decreases slower than any recursive
function.) as a limit from below
by considering
in the t'th computing step (time t) all programs of length t
which have already halted.
(This 'computation' suffers
from a radius of convergence which decreases slower than any recursive
function.) Third, the quantum 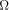 is complex. is complex.
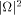 can be interpreted as a measure for the halting
probability of
C; i.e., the probability that an arbitrary (prefix-free) program
halts on C.
Both, the relative phases of approximations of can be interpreted as a measure for the halting
probability of
C; i.e., the probability that an arbitrary (prefix-free) program
halts on C.
Both, the relative phases of approximations of 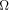 , as well as
approximations to , as well as
approximations to 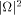 are measurable. are measurable. Finally, any measurements of 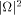 causes irreversible state collapses.
Since
causes irreversible state collapses.
Since 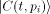 may not be in a
pure state, the series in
(7) and (8) will not be uniquely defined even for finite times.
The nondeterministic character of may not be in a
pure state, the series in
(7) and (8) will not be uniquely defined even for finite times.
The nondeterministic character of 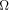 is not only based
on classical recursion theoretic arguments [1] but
also on the physical proposition that God plays the
quantum dice. is not only based
on classical recursion theoretic arguments [1] but
also on the physical proposition that God plays the
quantum dice.
[1] G. J. Chaitin, Information, Randomness and Incompleteness, Second edition
(World Scientific, Singapore, 1987, 1990);
Algorithmic Information Theory
(Cambridge University Press, Cambridge, 1987);
Information-Theoretic Incompleteness
(World Scientific, Singapore, 1992).
[2] R. M. Solovay, unpublished manuscript.
Page 203
[3] C. Calude,
Information and Randomness --- An Algorithmic Perspective
(Springer, Berlin, 1994).
[4] D. Z. Albert, Phys. Lett. 94A, 249 (1983).
[5] P. Benioff, J. Stat. Phys. 29, 515 (1982);
Phys. Rev. Lett. 48, 1581 (1982).
[6] D. Deutsch, Proc. R. Soc. Lond. A 400, 97 (1985).
[7] R. P. Feynman, Opt. News 11, 11 (1985).
[8] A. Peres, Phys. Rev. A32, 3266 (1985).
[9] P. Benioff, Annals New York Academy of Sciences 480, 475 (1986).
[10] N. Margolus, Annals New York Academy of Sciences 480, 487 (1986).
[11] D. Deutsch, Proc. R. Soc. Lond. A 425, 73 (1989).
[12] D. Deutsch and R. Jozsa, Proc. R. Soc. Lond. A 439, 553 (1992).
[13] A. Zeilinger,
Am. J. Phys. 49, 882 (1981);
M. Reck, A. Zeilinger, H. J. Bernstein and P. Bertani,
Phys. Rev. Lett. 73, 58 (1994).
[14] R. W. Hamming, Coding and Information Theory, Second Edition
(Prentice-Hall, Englewood Cliffs, New Jersey, 1980).
[15] K. Svozil, Randomness and Undecidability in Physics
(World Scientific, Singapore, 1993).
[16] K. Svozil,
On the computational power of physical systems,
undecidability, the consistency of phenomena and
the practical uses of paradoxa, in
International Conference on Fundamental Problems in
Quantum Theory, ed. by D. Greenberger (New
York Academy of Sciences, in print);
Quantum recursion theory, TU Vienna preprint.
[17] Let 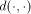 be the inner product of the Hilbert space.
Let further be be the inner product of the Hilbert space.
Let further be 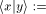
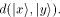 . Orthonormality states that . Orthonormality states that 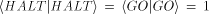 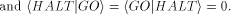 [18] R. J. Solomonoff, Information and Control 7, 1 (1964);
IEEE Transactions on Information Theory IT-24, 422 (1978).
[18] R. J. Solomonoff, Information and Control 7, 1 (1964);
IEEE Transactions on Information Theory IT-24, 422 (1978). Page 204
|
 introduced by Chaitin is generalized to quantum
computations.
introduced by Chaitin is generalized to quantum
computations.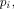 which, at time
which, at time 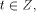 can be described by a quantum state
[
can be described by a quantum state
[
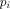 is
coded classically. That is, we choose a finite code alphabet A
and denote by A* the set of all strings over A.
Any program
is
coded classically. That is, we choose a finite code alphabet A
and denote by A* the set of all strings over A.
Any program 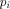 is coded as a classical sequence
is coded as a classical sequence 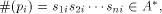
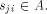 (In what follows,
(In what follows, 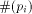 will be abbreviated by
will be abbreviated by 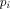 .)
We assume prefix coding
[
.)
We assume prefix coding
[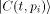 of the computer C with
program
of the computer C with
program 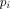 is
representable by quantum bits (qbits).
Every qbit is in a coherent superposition of the classical bit basis
is
representable by quantum bits (qbits).
Every qbit is in a coherent superposition of the classical bit basis 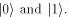 Assume that the states (1)
are orthogonal and normalized.
The computer C evolves according to a unitary
operator U such that (discrete time evolution)
Assume that the states (1)
are orthogonal and normalized.
The computer C evolves according to a unitary
operator U such that (discrete time evolution)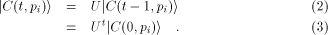

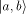 the halting bit.
The symbols
the halting bit.
The symbols 
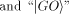 represent orthonormal vectors [
represent orthonormal vectors [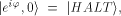
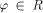 be the physical realization that the computer has
'halted;' likewise let
be the physical realization that the computer has
'halted;' likewise let 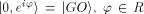 be the physical realization that the computer has not
`halted'.
Note that, since quantum computations are governed by unitary evolution
laws which are reversible, the halting state does not mean that the
computer does not change as time evolves. It just means that it has set
a signal --- the halting bit --- to indicated that it has finished its
task.
a and b are complex numbers which are a quantum mechanical measure
of the probability amplitude that the computer is in the halting and the
non-halting states, respectively.
(The corresponding probabilities are
be the physical realization that the computer has not
`halted'.
Note that, since quantum computations are governed by unitary evolution
laws which are reversible, the halting state does not mean that the
computer does not change as time evolves. It just means that it has set
a signal --- the halting bit --- to indicated that it has finished its
task.
a and b are complex numbers which are a quantum mechanical measure
of the probability amplitude that the computer is in the halting and the
non-halting states, respectively.
(The corresponding probabilities are 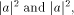 respectively.)
One
important feature of the quantum information concept ist that it does
not
merely allow two-valued states but a coherent superposition thereof.
respectively.)
One
important feature of the quantum information concept ist that it does
not
merely allow two-valued states but a coherent superposition thereof.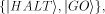 the computer C with classical input
the computer C with classical input 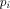 can be represented by
can be represented by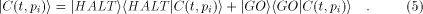
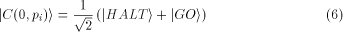
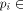 A*.
This corresponds to the fact that initially it is unknown whether or not
the computer halts on
A*.
This corresponds to the fact that initially it is unknown whether or not
the computer halts on  .
When during the time evolution the computer has completed its task,
the halting bit value is switched to
.
When during the time evolution the computer has completed its task,
the halting bit value is switched to
 by some internal operation,
otherwise it
remains in the coherent 50:50-superposition
of equation (6).
(Alternatively, the computer could be initially prepared
in the non-halting state
by some internal operation,
otherwise it
remains in the coherent 50:50-superposition
of equation (6).
(Alternatively, the computer could be initially prepared
in the non-halting state 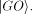 After completion of the
task, the halting bit is again
switched to
the halting state
After completion of the
task, the halting bit is again
switched to
the halting state 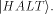 In this case, the subtractions of
In this case, the subtractions of 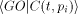 in
equations (7), (8) and (9) below would have to be eliminated.)
in
equations (7), (8) and (9) below would have to be eliminated.)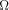 can be defined
as a weighted expectation over all computations of C with classical
input
can be defined
as a weighted expectation over all computations of C with classical
input 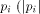 stands for the length of
stands for the length of 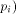
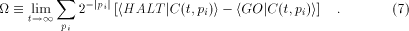
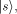
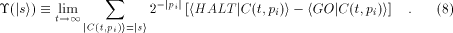
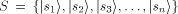 which correspond to mutually orthogonal
vectors in Hilbert space,
which correspond to mutually orthogonal
vectors in Hilbert space, 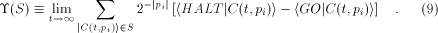
 but the comments apply to
but the comments apply to 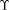 as well.)
as well.)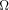 as a limit from below
by considering
in the t'th computing step (time t) all programs of length t
which have already halted.
(This 'computation' suffers
from a radius of convergence which decreases slower than any recursive
function.)
as a limit from below
by considering
in the t'th computing step (time t) all programs of length t
which have already halted.
(This 'computation' suffers
from a radius of convergence which decreases slower than any recursive
function.)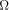 is complex.
is complex.
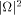 can be interpreted as a measure for the halting
probability of
C; i.e., the probability that an arbitrary (prefix-free) program
halts on C.
Both, the relative phases of approximations of
can be interpreted as a measure for the halting
probability of
C; i.e., the probability that an arbitrary (prefix-free) program
halts on C.
Both, the relative phases of approximations of 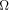 , as well as
approximations to
, as well as
approximations to 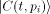 may not be in a
pure state, the series in
(7) and (8) will not be uniquely defined even for finite times.
The nondeterministic character of
may not be in a
pure state, the series in
(7) and (8) will not be uniquely defined even for finite times.
The nondeterministic character of 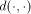 be the inner product of the Hilbert space.
Let further be
be the inner product of the Hilbert space.
Let further be 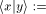
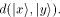 . Orthonormality states that
. Orthonormality states that