| Submission Procedure |
On Completeness of Pseudosimple Sets
(Odessa State University, Ukraine ul. Perekopskoj divizii 67-40 Odessa 270062, UKRAINE bulitko.odessa@REX.iasnet.com) Abstract: The paper contains completeness criterions for pseudosimple sets. Those criterions are constructed using effectivization of the definitions as well as extensionally bounded functions. Keywords: Completeness, Pseudosimple set, Effectivization, Extensionally bounded function Category: G 1 On Completeness of Pseudosimple SetsA recursively enumerable (r.e.) set is called complete (Turing-complete) if any r.e. set can be reduced to that set using Turing reducibility. Optionally complete sets can have some interesting properties, for instance they can be simple, pseudosimple, etc. Problems of constructing completeness criterions for simple sets by an effectivization of definitions have been investigated by McLaughlin, Smullyan, Lachlan, Arslanov, etc. History and systematical description of that can be found in [Arslanov 87]. Simple sets fall into class Most of our notation follows [Rogers 67] also r. means recursive, r.e.
means recursively enumerable and i.r.e. means
infinite recursively enumerable. We use Definition 1. A is pseudosimple Definition 2. A is pseudosimple with center C Above definitions allow the following effectivization: Definition 2'. A is weakly effectively
pseudosimple with center C First prove two complementary lemmas. Lemma 1. For any complete set A and any r.e. set M the following function is total and recursive in A:
Page 151 Proof. Therefore f is computable with oracle A. Lemma 2. Let A be complete and g be partial recursive in A. Then the following function is partial recursive in A:
Proof. Let us make computation of Theorem 1. (A is pseudosimple and complete) Proof.
f is computable with oracle A by lemma 1,2, and because
Another completeness criterion can be obtained introducing concept of special function. Definition 3. Let A be weakly effectively pseudosimple. We call total and recursive in A function f special for A if
Theorem 2. (A is pseudosimple and complete) Proof.
f can be computed with oracle A by lemmas 1,2, and because
Page 152
g can be computed with oracle A because f is recursive in A. Also g is total and obviously does not have fixed points so we can apply the Arslanov theorem that causes A is complete. There is also another approach to effectivization of the definitions. The approach is based on use of functions evaluating complexity characteristics of set other than the number of elements. For instance, Lachlan in [Lachlan 68] used the number of value changes of characteristic function for a given r.e. set on a cohesive set building sufficient conditions for complete maximal sets. Completeness criterion for maximal sets [Bulitko 92] constructed using Kolmogorov complexity of set initial segments is another example. Next step in that direction is use of extensionally bounded functions to construct completeness criterions for special classes of simple sets. That approach has been posed by V.K.Bulitko in [Bulitko 95]. In present paper we use that approach to describe pseudosimple and complete sets. Definition 4. Total f is extensionally bounded (e.b.)
Proof.
Let us consider pseudosimple sets with center. Theorem 4. (A is pseudosimple with recursive center C and
complete) Proof.
f is computable with oracle A by lemmas 1,2 and
Page 153 Situation regarding case of non-recursive (in general) center is described by the following theorems and remarkable enough. Trying to get the criterion we succeeded in way of using e.b functions only. Theorem 5. (A is weakly effectively pseudosimple with center C
recursive in A) Proof. Follows from the first theorem. Definition 5. Let A be weakly effectively pseudosimple with center C. Call total and computable with oracle A function f bounding for A if
Theorem 6. (A is weakly effectively pseudosimple with center C
and there is bounding for A function f) Proof. Define g as follows:
g can be computed with oracle A because f is recursive in A. Also g
is total and does not have fixed points. Thus A is complete by the
Arslanov theorem. Theorem 7. (A is pseudosimple with center C and complete)
Proof.
References
[Arslanov 87] Arslanov, M.M.: 'Local theory of unsolvability degrees and sets'; KGU press / Kazan, (1987).(In Russian). [Rogers 67] Rogers, H. Jr.: 'Theory of recursive functions and effective computability'; McGrow-Hill / N.-Y. (1967). [Lachlan 68] A.H.Lachlan, A. H.: 'Complete recursively enumerable sets'; Proc. Amer. Math. Soc., 19, (1968), 99-102. [Bulitko 92] Bulitko, V. K.: 'Subturing reducibilities with bounded complexity'; Izv. VUZov, ser. mat., 1 (1992), 27-37. (In Russian). [Bulitko 95] Bulitko, V. K.: 'On some complexity characteristics of Immune sets'; MLQ, 41, 3 (1995) (in press). Page 154
|
|||||||||||||||||
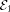 of r.e. set classification by
Uspenskij and Dekker-Myhill [
of r.e. set classification by
Uspenskij and Dekker-Myhill [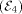 the
criterions have been constructed even before. However we do not know any
specific criterion for pseudosimple
the
criterions have been constructed even before. However we do not know any
specific criterion for pseudosimple 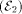 and pseudocreative
and pseudocreative 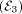 sets.
In this paper we propose some completeness criterions for
pseudosimple sets.
sets.
In this paper we propose some completeness criterions for
pseudosimple sets.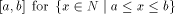 and
and  as '
as '  under definition'. Sometimes we use 'number of' as
'index of'. Let us recall the following definitions from [
under definition'. Sometimes we use 'number of' as
'index of'. Let us recall the following definitions from [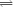 (1) A is r.e. but not r.;
(1) A is r.e. but not r.; 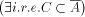
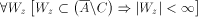 . Such C we will denote
. Such C we will denote 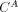 .
. (1)
A is pseudosimple;
(1)
A is pseudosimple; 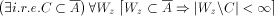
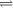 (1) A is pseudosimple;
(1) A is pseudosimple;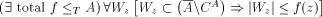
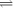 (1) A is
pseudosimple with center C; (2)
(1) A is
pseudosimple with center C; (2) 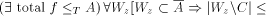
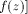
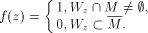
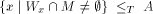 because
because
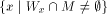 is an r.e. set.
is an r.e. set.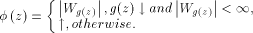
 as follows. Given z we
start computation of g(z) and if it ends, we enumerate numbers of r.e.
sets
as follows. Given z we
start computation of g(z) and if it ends, we enumerate numbers of r.e.
sets 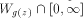
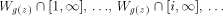 until some of them fall into
until some of them fall into 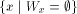 which
is recursive in A. Let it happen when i=n so we set
which
is recursive in A. Let it happen when i=n so we set 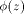 equal to
equal to 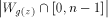 .
Note we use uniform
recursiveness of
.
Note we use uniform
recursiveness of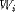 in respect to complete A.
in respect to complete A.
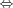 (A
is weakly effectively pseudosimple and
(A
is weakly effectively pseudosimple and 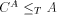 ).
).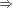 Let A be pseudosimple and complete then
obviously
Let A be pseudosimple and complete then
obviously 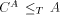 . Define total f as follows:
. Define total f as follows: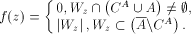
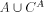 is an
r.e. set, and
is an
r.e. set, and 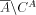 is immune. Thus A is weakly
effectively pseudosimple.
is immune. Thus A is weakly
effectively pseudosimple.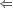 Using f, which is recursive in A, and possibility to
write out elements of
Using f, which is recursive in A, and possibility to
write out elements of 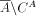 in increasing order with
oracle A, construct initial segment
in increasing order with
oracle A, construct initial segment 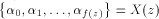 of enumeration of
of enumeration of 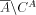 in increasing order. An r.e. index of X(z) can be computed with oracle A
because X(z) is finite and recursive in A. Let g(z) be that r.e.
index. So
in increasing order. An r.e. index of X(z) can be computed with oracle A
because X(z) is finite and recursive in A. Let g(z) be that r.e.
index. So 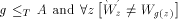 . Thus A
is complete by the Arslanov theorem [
. Thus A
is complete by the Arslanov theorem [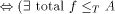
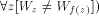 .
.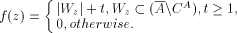
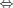 (A
is weakly effectively pseudosimple and there is f special for A).
(A
is weakly effectively pseudosimple and there is f special for A).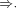 Define f as follows:
Define f as follows: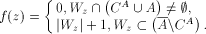
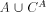 is an r.e. set, and
is an r.e. set, and 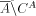 is immune. So A is weakly
effectively pseudosimple with special function f.
is immune. So A is weakly
effectively pseudosimple with special function f.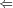 Let g be defined as follows:
Let g be defined as follows: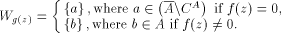
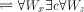
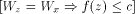
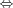 (A
is r.e. but not r. &
(A
is r.e. but not r. & 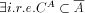 such that
the following function f:
is e.b. and recursive in A).
such that
the following function f:
is e.b. and recursive in A).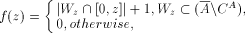
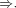 Obviously A is r.e. but not r. f is
computable with oracle A by lemma 1 and because
Obviously A is r.e. but not r. f is
computable with oracle A by lemma 1 and because 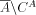 is immune.
For any number i of r.e.
is immune.
For any number i of r.e. 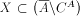 f(i) is bounded by cardinality of X that is
finite because A is pseudosimple. f is equal to 0 for a number of an
r.e. set which is not a subset of
f(i) is bounded by cardinality of X that is
finite because A is pseudosimple. f is equal to 0 for a number of an
r.e. set which is not a subset of 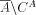 . Therefore f
is e.b.
. Therefore f
is e.b. Assume
Assume 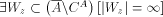 .
Then taking in
account infiniteness of
.
Then taking in
account infiniteness of 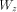 index set we get f is not bounded on
index set we get f is not bounded on 
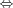 (A is weakly effectively pseudosimple with
recursive center C).
(A is weakly effectively pseudosimple with
recursive center C).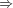 Define f as follows:
Define f as follows: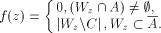
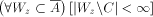 .
Therefore A is weakly effectively pseudosimple with recursive
center.
.
Therefore A is weakly effectively pseudosimple with recursive
center.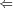 We can get total function
We can get total function 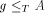 that does not have
fixed points doing in the same way as in the first theorem. Using the
Arslanov theorem we obtain completeness of A.
that does not have
fixed points doing in the same way as in the first theorem. Using the
Arslanov theorem we obtain completeness of A. 
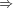 (A is pseudosimple with center C and
complete).
(A is pseudosimple with center C and
complete).
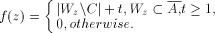
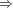 (A is
pseudosimple with center C and complete).
(A is
pseudosimple with center C and complete).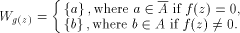

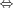 (A is r.e. but not r.;
(A is r.e. but not r.; 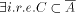 ;
the following f is e.b. and computable with oracle A):
;
the following f is e.b. and computable with oracle A): 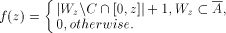
 Obviously A is r.e. but not r. f is
computable with oracle A by lemma 1 and because having oracle A we are
able to write out all of
Obviously A is r.e. but not r. f is
computable with oracle A by lemma 1 and because having oracle A we are
able to write out all of 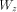 elements not belonging to C and situated in
elements not belonging to C and situated in
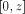 f is e.b. because f is bounded on numbers of r.e.
f is e.b. because f is bounded on numbers of r.e.
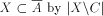 which is finite
because A is pseudosimple with center, and f is equal to 0 on numbers of
an r.e. set which is not a subset of
which is finite
because A is pseudosimple with center, and f is equal to 0 on numbers of
an r.e. set which is not a subset of 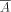 .
.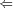 A is pseudosimple with center C because f is e.b. and
therefore
A is pseudosimple with center C because f is e.b. and
therefore 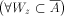
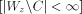 (otherwise we would get unbounded f
taking in account that any r.e. set has an infinite number of its
indexes). Completeness of A can be proved in the same way as in theorem 6.
(otherwise we would get unbounded f
taking in account that any r.e. set has an infinite number of its
indexes). Completeness of A can be proved in the same way as in theorem 6. 