| Submission Procedure |
Exploiting Parallelism in Constraint Satisfaction for Qualitative Simulation
(Graz University of Technology, Austria marco@iti.tu-graz.ac.at) (Graz University of Technology, Austria rinner@iti.tu-graz.ac.at) (Graz University of Technology, Austria rweiss@iti.tu-graz.ac.at) Abstract: Constraint satisfaction is very common in many artificial intelligence applications. This paper presents results from parallelizing constraint satisfaction in a special application --- the algorithm for qualitative simulation QSim [Kuipers 94]. A parallel-agent based strategy (PAB) is used to solve the constraint satisfaction problem (CSP). Two essential steps of PAB are studied in more detail to achieve a good performance of the parallel algorithm. Partitioning heuristics to generate independent parts of the overall search space are investigated. Sequential CSP algorithms are compared in order to reveal the most efficient one for QSim. The evaluation of these heuristics and algorithms is based on runtime measurements using CSPs traced from QSim. These runtimes allow a best- and worst-case estimation of the expected speedup of the parallel algorithms. The comparison of sequential CSP algorithms leads to following strategy for solving partitioned problems. Less complex problems are solved with simple backtracking, and more complex models are solved with graph-directed backjumping (GBJ). Key Words: Parallel constraint satisfaction, QSim, distributed AI 1 Introduction
Constraint satisfaction is very common in artificial intelligence applications, and it is also a basic operation in qualitative simulation. Constraint satisfaction problems (CSP) are often solved by backtracking algorithms, which find solutions with depth-first search. Many sequential and parallel algorithms have been developed to solve CSPs more efficiently. This paper presents results of our work in parallelizing and distributing constraint satisfaction for the special application QSim. QSim, the widely-used algorithm for qualitative simulation, has been developed by Kuipers [Kuipers 94]. Qualitative simulation is a new and challenging simulation paradigm. Major areas of qualitative simulation applications are design, monitoring, and fault-diagnosis. A drawback of current QSim implementations is poor execution speed. In our research project [Platzner, Rinner, Weiss 95] a special-purpose computer architecture for QSim is developed to improve the performance. Better performance is achieved by SW/HW-migration of frequently Page 811
used primitive functions, and mapping QSim kernel functions onto a multiprocessor system. The overall application-specific computer architecture consists of digital signal processors TMS320C40 which are equipped with specialized FPGA-based coprocessors for executing the primitive functions. 2 Constraint Satisfaction in QSim
A constraint satisfaction problem can be informally described as follows: Given a set of n variables each with an associated domain, and given a set of constraints each involving a subset of the variables, find an n-tuple such that this n-tuple is an instantiation of the n variables satisfying all constraints. A more formal description can be found in [Dechter 92]. Constraint satisfaction is a basic operation in the qualitative simulator QSim. It is used to determine all possible successors of a given qualitative state --- i.e. calculating all solutions of a CSP, specified by a constraint network (variables and constraints) and possible values of all variables (domains). In QSim CSPs are represented dual to the representation in [Mackworth 77]. The nodes of the constraint graph correspond to constraints, and the edges between the nodes correspond to variables. A constraint graph of a QSim example is shown in [Figure 1]. This dual representation is used because the arity of QSim constraints is not limited by 2. Since solving CSPs is NP-complete, preprocessing or filtering steps
before backtracking can eliminate large parts of the overall search
space [Mohr, Henderson 86]. These techniques are node, arc, and path
consistency and are widely applied in constraint satisfaction. In QSim
node consistency is achieved by the constraint-filter. For each QSim
constraint all possible tuples of the attached variables are checked
against the constraint conditions. Tuples violating these conditions
are discarded. Arc consistency is achieved by the Waltz-filter, which
eliminates inconsistencies between adjacent constraints. Each tuple
associated with constraint Page 812 the remaining tuples and thus all solutions of the CSP. A simple backtracking algorithm is used for this depth-first search. Increased performance is achieved by interleaving node and arc consistency algorithms and by a heuristic ordering of the constraints for the backtracking step. There are many techniques exploiting the parallelism of these filtering steps [Conrad, Agrawal, Bahler 92][Cooper, Swain 92]. We also parallelize the node and arc consistency algorithm of QSim in our research project, but in this paper we present only the results in parallelizing and distributing the backtracking algorithm [Riedl 95]. CSPs in QSim have special characteristics which are different from many other CSPs. These characteristics have to be considered in selecting appropriate algorithms and parallelizing techniques as presented in the next section.
 Calculating the initial states from an incomplete state description can lead to more than 4 values of individual variables. Calculating the initial states from an incomplete state description can lead to more than 4 values of individual variables.3 Parallel Constraint Satisfaction
3.1 Existing Algorithms
Many parallel algorithms for constraint satisfaction are known in
literature. Luo, Hendry, and Buchanan [Luo, Hendry, Buchanan 94] have
classified the most common algorithms as distributed-agent-based
(DAB), parallel-agent-based (PAB), and functional-agent-based
(FAB). Different strategies involve different control structures,
problem spaces, and communication methods. The FAB strategy can be
excluded from further considerations, because it requires shared
memory architectures. Important features of the remaining strategies
can be summarized as follows.
Our application-specific computer architecture has to fulfill several requirements, which obviously influence the parallelization of the constraint satisfaction algorithm. The following requirements are of special interest.
There are several reasons for choosing a PAB strategy for our application. First, it is an excellent strategy for finding all solutions of a given CSP and it is an inherent scalable algorithm. Second, the PAB strategy can be applied to problems with arbitrary structure. Finally, the independent search spaces can be solved with any sequential (and optimized) algorithm. A detailed comparison between DAB and PAB strategies can be found in [Luo, Hendry, Buchanan 94]. In the next two subsections, we consider the essential steps of PAB in more detail --- we investigate methods to achieve a good partitioning of the complete search space, and compare sequential algorithms to use the best one for QSim- models and their partitioned subproblems. 3.2 Generating Independent Subproblems
3.2.1 Evaluation and Speedup Estimation
Partitioning of the complete search space is essential for
an efficient parallel algorithm. The partitioning methods are
evaluated using runtimes of the subproblems. The most interesting
runtimes are the overall runtime Using these runtimes ( The worst-case condition is satisfied if the longest task is scheduled last and all other tasks are equally distributed among the processors. The worst case runtime of the parallel algorithm can be given as 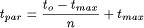
Page 814 For best case estimation we have to consider two cases. If the number
of processors is greater than 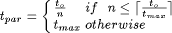 3.2.2 Partitioning Methods
Two partitioning methods are investigated --- constraint-based partitioning and variable-based partitioning.
3.3 Solving the Subproblems
With the parallel CSP strategy PAB the individual subproblems can be solved with any sequential algorithm. QSim uses a simple backtracking algorithm, extended by a constraint ordering scheme, for this task. There are many extensions and improvements of simple backtracking known in literature. [Prosser 93] Page 815 presents an overview of possible improvements, other enhancement schemes are also presented in [Dechter 90]. Most of these improvements were evaluated with standard CSP benchmarks (ZEBRA problem, N-queens, randomly generated CSPs, etc.). QSim CSPs have different characteristics than those benchmark CSPs. Obviously we are interested in fast algorithms for QSim CSPs. Therefore, we evaluate improved backtracking algorithms with CSPs traced from QSim. These algorithms are: FC (forward checker), CBJ (conflict-directed backjumping), and GBJ (graph-directed backjumping). A simple backtracking algorithm (BT) is also executed as a reference. The implementation of these algorithms is based on [Kondrak 94] and the CSP-library of [Beck 94]. 4 Experimental Results
4.1 QSim CSPs
To obtain realistic results from our measurements, three different QSim models have been simulated and the generated CSPs have been traced. Two simulation models were chosen from the QSim-package. The Starling model (STLG) has 17 variables and 18 constraints, and the Heart model (HEART) consists of 28 variables and 21 constraints. The Reaction-Control-System (RCS) [Kay 92], which is not included in the QSim-package, is the most complex model we have traced. It consists of 45 variables and 48 constraints. 8 to 16 CSPs with different complexity --- different cardinality of the variables' domains --- were chosen from the big number of CSPs generated during qsim runs. The CSPs were executed on a digital signal processor TMS320C40. The runtimes of all backtracking algorithms were measured with the internal hardware timer of this processor. 4.2 Partitioning Methods
The most interesting runtimes for evaluating the two partitioning
methods (CBP and VBP) and its variants are presented in [Table 1] and
[Table 2]. Only the runtime of the backtracking algorithm for solving
the subproblems is shown in these tables. The overall runtime A further interesting point is the influence of the number of
generated subproblems to Due to the exploitation of the dependencies between adjacent
constraints, the VBP method achieves better results than
CBP. Especially, the big increase of the overall runtime Page 816
Table 1: CBP method. All runtimes of CSPs of an individual QSim model are summarized and are presented in the corresponding row. The runtimes are measured on a digital signal processor TMS320C40. The runtimes for the single-processor algorithm are 6.12 ms for STLG, 25.72 ms for HEART, and 726 ms for RCS.
Table 2: VBP method. All runtimes of CSPs of an individual QSim model are summarized and are presented in the corresponding row. The runtimes for the single-processor algorithm are 6.83 ms for STLG, 28.77 ms for HEART, and 805.63 ms for RCS. The small increase compared to the single-processor runtimes of CBP is due to different memory mappings of the target system. Speedup Estimation of VBP A comparison of the speedup estimation for VBP-INST and VBP-CON is shown in [Figure 2]. In most cases VBP-CON outperforms VBP-INST --- especially for complex CSPs (model RCS). VBP-CON results in a linear speedup for worst- and best-case estimation. It turns out that the length of the maximum task limits the expected speedup for VBP-INST. Speedup increases with the number of generated tasks. However, the more tasks are generated the more overall communication time is required and the speedup of highly partitioned CSP can be lost. Best results are expected with VBP-CON and a medium number of tasks. Page 817
4.3 Comparison of Single-Processor CSP Algorithms
The CSPs of the three QSim models have been solved with different sequential algorithms. We have tried to find a parameter to estimate the runtime of a given CSP. The average number of tuples per constraint (T/C) was chosen as such a parameter. A plot of the runtimes is presented in [Figure 3]. The CSPs are ordered corresponding to this parameter. It turns out that simple backtracking is the fastest algorithm for simple QSim models. For complex models sophisticated algorithms perform better. Graphdirected backjumping (GBJ) has the shortest runtime on almost all complex models. Thus, the parameter T/C can be used to divide QSim CSPs into two parts. Simple CSPs (T/C is smaller than a given limit) should be solved with simple backtracking, the other CSPs should be solved with the GBJ algorithm. Page 818 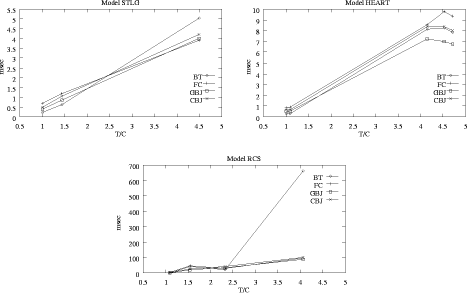 Figure 3: Comparison of sequential backtracking algorithms. The CSPs
are ordered to the average number of tuples per constraint (T/C). For
simple CSPs BT performs better than the other algorithms. On more
complex CSPs the opposite is true --- especially GBJ is up to 7 times
faster than BT for RCS at T/C = 4.
Figure 3: Comparison of sequential backtracking algorithms. The CSPs
are ordered to the average number of tuples per constraint (T/C). For
simple CSPs BT performs better than the other algorithms. On more
complex CSPs the opposite is true --- especially GBJ is up to 7 times
faster than BT for RCS at T/C = 4.5 Conclusions
In this paper we have presented a parallelizing strategy for constraint satisfaction in QSim. Two important steps of the PAB strategy are studied in detail. First, partitioning methods for the CSP are introduced and evaluated. The evaluation of these methods is based on runtime measurements of the subproblems and a worst- and best-case speedup estimation. Second, different sequential backtracking algorithms are compared using QSim CSPs. Results from this work can be summarized as follows.
Page 819 References
[Beck 94] Peter van Beck.: ``CSP Library''; Department of Computing Science, University of Alberta (1994), library of CSP algorithms. [Conrad, Agrawal, Bahler 92] James M. Conrad, Dharma P. Agrawal, and Dennis R. Bahler.: ``Scalable Parallel Arc Consistency Algorithms for Shared Memory Computers''; Proceedings 6th International Parallel Processing Symposium, IEEE, Los Alamitos, CA, (1992), 242-249. [Cooper, Swain 92] Paul R. Cooper and Michael J. Swain.: ``Arc consistency: parallelism and domain dependence''; Artificial Intelligence, 58 (1992), 207-235. [Dechter 90] Rina Dechter.: ``Enhancement Schemes for Constraint Processing: Backjumping, Learning, and Cutset Decomposition''; Artificial Intelligence, 41 (1990), 273-312. [Dechter 92] Rina Dechter.: ``Constraint Networks''; Stuart C. Shapiro, editor, Encyclopedia of Artificial Intelligence, John Wiley & Sons, 1 (1992), 276-285. [Kay 92] Herbert Kay.: ``A qualitative model of the space shuttle reaction control system''; Technical Report AI92-188, Artificial Intelligence Laboratory, University of Texas (1992). [Kondrak 94] Grzegorz Kondrak.: ``A Theoretical Evaluation of Selected Backtracking Algorithms''; Master's thesis, Department of Computing Science, University of Alberta (1994) [Kuipers 94] Benjamin Kuipers.: ``Qualitative Reasoning: Modeling and Simulation with Incomplete Knowledge''; Artificial Intelligence, MIT Press (1994) [Luo, Hendry, Buchanan 94] Q.P. Luo, P.G. Hendry, and J.T. Buchanan.: ``Strategies for Distributed Constraint Satisfaction Problems''; Proceedings 13th International DAI Workshop, DAI, Seattle, WA (1994) [Mackworth 77] Alan K. Mackworth.: ``Consistency in Networks of Relations''; Artificial Intelligence, 8 (1977), 99-118. [Mohr, Henderson 86] Roger Mohr and Thomas C. Henderson.: ``Arc and Path Consistency Revised''; Artificial Intelligence, 28 (1986), 225-233. [Platzner, Rinner, Weiss 95] Marco Platzner, Bernhard Rinner, and Reinhold Weiss.: ``A Distributed Computer Architecture for Qualitative Simulation Based on a Multi-DSP and FPGAs''; 3rd Euromicro Workshop on Parallel and Distributed Processing, IEEE Computer Society Press, San Remo (1995), 311-318. [Prosser 93] Patrick Prosser.: ``Hybrid Algorithms for the Constraint Satisfaction Problem''; Computational Intelligence, 9, 3 (1993) 268-299. [Rao, Kumar 93] V. Nageshwara Rao and Vipin Kumar.: ``On the Efficiency of Parallel Backtracking''; IEEE Transactions on Parallel and Distributed Systems, 4, 4(1993), 427-437. [Riedl 95] Johannes Riedl.: ``Parallele Algorithmen und Laufzeitmessungen für Constraint Satisfaction im qualitativen Simulator QSim''; Master's thesis, Institute for Technical Informatics, Graz University of Technology (1995) Acknowledgements This project is partially supported by the Austrian National Science Foundation Fonds zur Förderung der wissenschaftlichen Forschung under grant number P10411-MAT. Page 820
|
|||||||||||||||||
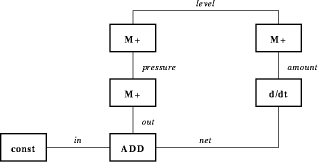 Figure 1: Constraint graph of the QSim bathtub model. Constraints are
represented by the nodes of the graph. The constraint arity ranges
from 1 to 3. Edges between nodes correspond to shared variables. Sets
of valid tuples are attached to all constraints after
constraint-filtering.
Figure 1: Constraint graph of the QSim bathtub model. Constraints are
represented by the nodes of the graph. The constraint arity ranges
from 1 to 3. Edges between nodes correspond to shared variables. Sets
of valid tuples are attached to all constraints after
constraint-filtering.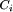 is discarded unless the same value of
the shared variable is assigned in at least one tuple of each adjacent
constraints. Path consistency is not currently used in QSim. The final
backtracking step generates all valid assignments of
is discarded unless the same value of
the shared variable is assigned in at least one tuple of each adjacent
constraints. Path consistency is not currently used in QSim. The final
backtracking step generates all valid assignments of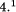
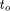 , which is the sum of the runtimes of
all subproblems, the maximum runtime of all subproblems
, which is the sum of the runtimes of
all subproblems, the maximum runtime of all subproblems 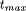 , and the
sequential runtime of the unpartitioned problem
, and the
sequential runtime of the unpartitioned problem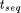 . Due to redundancies
in the independent subproblems the overall runtime
. Due to redundancies
in the independent subproblems the overall runtime 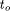 can be longer
than
can be longer
than 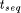 . An efficient partitioning method keeps the overall
runtime small. If
. An efficient partitioning method keeps the overall
runtime small. If 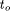 gets smaller than
gets smaller than 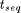 a superlinear speedup is
expected. The subproblem with the longest runtime restricts the
maximum speedup. Thus, a balanced partitioning, where all subproblems
have nearly the same runtime, should be achieved.
a superlinear speedup is
expected. The subproblem with the longest runtime restricts the
maximum speedup. Thus, a balanced partitioning, where all subproblems
have nearly the same runtime, should be achieved.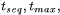 and
and 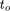 ), it is possible to estimate the speedup
of the parallel algorithm. Communication times are not considered in
this estimation, and simple task attraction is assumed to schedule
tasks to free processors. We determine the limits of the speedup by
worst- and best-case estimation. First of all, the speedup is defined
as S(n) =
), it is possible to estimate the speedup
of the parallel algorithm. Communication times are not considered in
this estimation, and simple task attraction is assumed to schedule
tasks to free processors. We determine the limits of the speedup by
worst- and best-case estimation. First of all, the speedup is defined
as S(n) =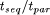 , where
, where 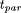 denotes the runtime using n processors.
denotes the runtime using n processors.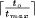 the parallel runtime is limited by
the parallel runtime is limited by 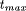 ,
otherwise all tasks are equally divided among the processors. More
formally, the best case parallel runtime can be estimated as
,
otherwise all tasks are equally divided among the processors. More
formally, the best case parallel runtime can be estimated as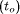 and the
maximum runtime
and the
maximum runtime 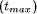 of all subproblems are summarized for all
CSPs of an individual model. The sums are presented in the
corresponding rows of the table. All subproblems were solved with the
simple backtracking algorithm as used in QSim.
of all subproblems are summarized for all
CSPs of an individual model. The sums are presented in the
corresponding rows of the table. All subproblems were solved with the
simple backtracking algorithm as used in QSim. 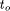 and
and 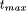 . Three cases are considered
--- the CSP is partitioned into at most 16, at most 64, and at most
256 subproblems. The corresponding runtimes are also presented in the
tables.
. Three cases are considered
--- the CSP is partitioned into at most 16, at most 64, and at most
256 subproblems. The corresponding runtimes are also presented in the
tables. 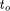 and the
size of the maximum subtask
and the
size of the maximum subtask 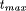 lead to poor parallel performance
with CBP. VBP generates shorter maximum subtasks, and in some cases
lead to poor parallel performance
with CBP. VBP generates shorter maximum subtasks, and in some cases  is shorter than the runtime of the single-processor algorithm.
is shorter than the runtime of the single-processor algorithm.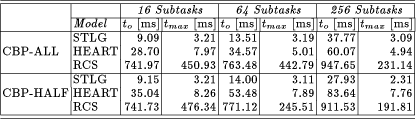
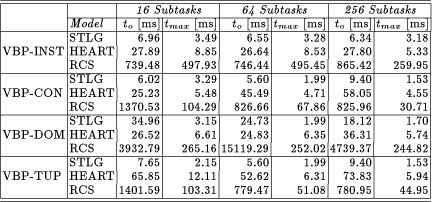
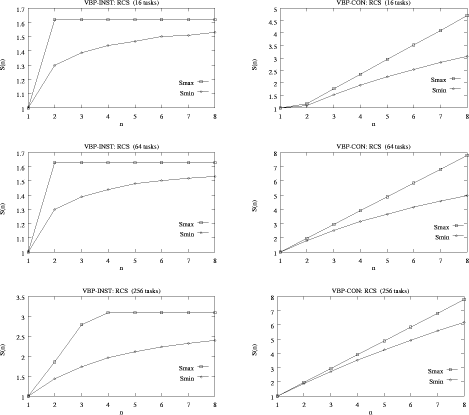 Figure 2: Speedup estimation of VBP for the RCS model. Worst- and
best-case speedup for VBP-INST and VBP-CON are shown in the left and
right column plots. Especially for complex models VBP-CON performs
better than VBP-INST.
Figure 2: Speedup estimation of VBP for the RCS model. Worst- and
best-case speedup for VBP-INST and VBP-CON are shown in the left and
right column plots. Especially for complex models VBP-CON performs
better than VBP-INST.