| Submission Procedure |
|
|
|
|||||||||||||||
High-radix Division with Approximate Quotient-digit Estimation
Department of Computer Science, The University of Auckland, Private Bag 92019, Auckland, New Zealand p_fenwick@cs.auckland.ac.nz Abstract: High-radix division, developing several quotient bits per clock, is usually limited by the difficulty of generating accurate high-radix quotient digits. This paper describes techniques which allow quotient digits to be inaccurate, but then refine the result. We thereby obtain dividers with slightly reduced performance, but with much simplified logic. For example, a nominal radix-64 divider can generate an average of 4.5 to 5.5 quotient bits per cycle with quite simple digit estimation logic. The paper investigates the technique for radices of 8, 16, 64 and 256, including various qualities of digit estimation, and operation with restricted sets of divisor multiples. Keywords: Division, high radix, approximate digit estimates Category: B2 1 Introduction
Division has always been one of the more difficult of the fundamental operations in computers. Some very early computers omitted it altogether, even if they included multiplication, relying on one of the multiplicative algorithms mentioned later. (Many modern super-computers also follow this well-established historical precedent!) Division was often restricted to basic restoring or non-restoring methods which develop only one bit per cycle, even on computers where multiplication handled two or more bits per cycle. There are several methods for achieving binary division which is faster than the simple non-restoring method.
The work of this paper is in many ways a return to the traditional subtractive methods, but emphasises the combination of high-radix division (to minimise the time for a division) with relatively simple logic for quotient digit estimation (to minimise complexity and cost) and a minimal set of divisor multiples (again for complexity and cost). A unique feature is the trade-off between performance and complexity; without changing the basic design it is possible to reduce the available divisor multiples or the accuracy of the quotient digit estimation (or both) at the cost of only slightly slower division operation. 2 The Basic Principles of "Subtractive Division"
All of the subtractive methods depend on the relation below, as stated by Atkins 1961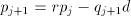 
Page 3
where Verbally, we can note that we subtract a multiple ( [Knuth 1969] (p235) shows that for any radix r, estimating the quotient digit by taking the two most-significant residue digits divided by one most-significant divisor digit will give an error of at most 2 in the estimate; he includes a refinement which ensures that the digit is usually exact, may be in error by 1, and never has an error of 2. The refinement is, however relatively expensive to implement and he does not discuss the necessary hardware. (It does however have interesting connections with the more recent techniques for producing very accurate quotient estimates.) [Atkins 1970] presents an extensive analysis of SRT division and its extension to higher radices. He discusses redundancy of the quotient representation (for example, 3 may be represented as either 2+1 or 4-1) and states that With redundancy, the quotient digit need not be precise. Then from a detailed analysis of digitestimation logic, he shows that the number of bits to be examined is at least Residue bits Divisor bits where the radix r is
Radix Residue Divisor
bits bits
4 5 7
8 6 8
16 7 9
64 9 11
256 11 13
Table 1. Atkins estimates ofbits to be examined Page 4 For some typical radices, we find that the number of operand bits to be examined is as shown in [Tab. 1]. These results show that quotient estimation for high radix division is indeed a difficult process; even for radix 16 it is a function of at least 16 inputs. Atkins also discusses the problems of converting the quotient from the redundant code in which it is generated into the external binary form and states that a full-length quotient subtracter may be necessary. (This matter will considered later.) A recent paper [Montuschi and Ciminiera 1994] considers the use of overredundant digits, where the quotient digits may equal or exceed the division radix. In the present context their most important result is that the quotient-digit estimation logic may be simplified by allowing a wider range of quotient digits. Many of their comments (and the over-redundant digits) are germane to the present work, but here we also allow the quotient digits to be inaccurate. 3 The new approach
Underlying most of this paper is the observation that at any stage of
the division with divisor d the 'residue' p and 'partial quotient' q
represent a value The new method involves placing a small low-precision adder at the low-order end of the quotient so that new digits are added into the quotient rather than jammed in as is usual. We also allow unshifted arithmetic to refine the quotient digit estimate, effectively holding the division at a particular stage until its result is satisfactory. We can use any multiple which we like, or any convenient combination of multiples, in constructing each quotient digit. In particular we do not insist that the generated quotient digit will immediately reduce the residue to the correct range, but are prepared to accept a poor estimate and then repair the damage from that estimate. There are two consequences -
The second aspect is especially interesting. While it is relatively easy to provide logic which gives a good quotient estimate most of the time, it is much more difficult (and expensive) to generate an accurate value all of the time. (This complexity is evident from the results of Atkins, especially when compared with the look-up table sizes used here.) With a correction step available at any stage a bad estimate need not affect the final answer - it just requires a little longer to fix up. We can therefore trade off the complexity of the estimation logic against the overall division speed. 4 Limiting the quotient carry propagation.
An assumption of the present work is that the quotient has a short adder; a full-length quotient adder requires a considerable increase in logic complexity and should be avoided if possible. (This is exactly the situation discussed by Atkins and mentioned above in converting from redundantly-represented quotient digits.) For a positive divisor, excessive quotient carry arises when the residue becomes negative after a subtraction and remains negative for a while thereafter. With conventional non-restoring division, the negative value will force a 0 quotient bit to be entered (from an unsuccessful subtraction). By comparison, the algorithm as described enters the multiple which was used (and was too large) and relies on a later negative digit to correct for the overdraw. If there is only a slight overdraw, the residue stays close to zero for several steps while zero quotient digits are generated and the carry must eventually propagate through all of these zero digits. To minimise the quotient carry propagation, we monitor the sign of the result and, if it is negative, enter as a quotient digit the (multiple-1) and set a Qcarry flag; this is analogous to the action of simple non-restoring division. Qcarry is shifted in parallel with the quotient and added in on the next cycle. Thus we subtract 1 from the quotient, but add it back on the next cycle. The operation is similar during a correction cycle, except that the 1 is added directly into the quotient, without any shift. To illustrate, consider a radix-8 divider where the residue goes just negative from a multiple of 6 and stays negative with no arithmetic (0 digit) for several cycles before being corrected with a -2 multiple. Assuming that the simple algorithm generates the quotient digit sequence Page 6 { 6 0 0 -2 }, the generated quotient bits are { 110 000 000 } before the last digit and become the correct value { 101 111 111 110 } after the -2 multiple is added, but only after the carry propagates through 8 bits of the previous quotient. With the Qcarry flag, we recognise the overdraw and enter an initial 5 instead of 6; this digit is now correct. On the next two cycles the generated digit of 0 is converted to -1 because of the negative residue, but the shifted Qcarry corresponds to an addition of 8, so the entered digit is 7 or bit pattern 111. We enter the correct quotient digit at each stage, avoiding lengthy carry propagation. We may note that the Qcarry is in fact redundant, being identical to the residue sign. It is however convenient to regard it as a separate entity connected with the quotient rather than the residue. The carry from the main adder wraps-round into the quotient adder. 5 The complete division algorithm.
The final algorithm is shown in [Fig. 1], written in C but with some conditions in descriptive rather than explicit form. The function estDigit produces a suitable quotient digit estimate by some means (in the tests by a table lookup), including operations such as the limitation to complex multiples as described in [Section 11]. This program, and indeed all of the work in the paper, assumes a positive divisor.
while (dividing)
{
Residue <<= BitsPerDigit; /* align residue */
Qdigit = estDigit (Residue, Divisor); /* estimate quot. digit */
Residue -= Qdigit * Divisor; /* adjust residue */
Quotient =
((Quotient + Qcarry) << BitsPerDigit) + Qdigit;
Qcarry = (Residue <0); /* to stop long carries */
Quotient -= Qcarry; /* and adjust quotient */
while (Residue_out_of_range) /* correction cycles */
{
Qdigit = estDigit (Residue, Divisor); /* est. quot. digit */
Residue -= Qdigit * Divisor; /* adjust residue */
Quotient += Qdigit + Qcarry; /* adjust quotient */
Qcarry = (Residue < 0);
Quotient -= Qcarry;
}
} /* end main divide loop */
if (Qcarry > 0) Quotient++; /* assimilate quotient carry */
while (Residue < 0) /* correction if -ve residue */
{ Residue += Divisor; Quotient--; }
Figure 1. The basic division program Page 7 The first four lines of the main loop are essentially a standard high-radix division and are followed by two lines to control the quotient carry propagation. An inner loop handles the case of the residue being not reduced correctly, using code which is very similar to the main division code but without operand shifts. Finally, after the main loop is complete, we must assimilate any pending Qcarry and correct for a residue of the wrong sign. A point which is not stated is that digit estimation in the inner, correction, loop must never give a zero digit because this loop must always change the residue; the digit must be forced to +1 or -1 depending on the sign of the residue. 6 The Hardware
The basic divider hardware is shown in [Fig. 2]. The differences from conventional division hardware are in the presence of the quotient adder and in the ability to operate in an unshifted mode during division. The quotient is shown with two paths from the quotient register, one shifted and one unshifted; the same applies to the residue register and main adder. Two shifts are wired into the residue and quotient logic; a shift of 3, 4, etc bits which determines the nominal radix of the operation and a zero shift which is used during correction cycles.
Figure 2. Divider Hardware In many cases the divisor multiple logic is limited to a 2-input adder/subtracter with shifters at each input up to the width of a quotient digit. Page 8 7 Simple, radix-8, division
The proposed algorithm was simulated by program using 32-bit integers and 64-bit long integers to provide a basic operand precision of 24 bits (48 bit dividend). In all cases the high-order bits of the divisor and residue are used to index a pre-computed table which yields the estimated multiple. The divisor is assumed normalised with its most-significant bit always 1. The initial tests are with radix-8 division (3 bits per cycle). The test cases were -
All cases were tested by a sequence of 100,000 divisions (the same sequence in all cases) counting the total add/subtract operations or cycles, the number of times that an earlier quotient was adjusted, and the number of additional correction cycles needed. With 8 octal digits to be developed for each 24-bit test operand, there are 8 'basic operations' for each test case, or 800,000 operations within each test. The results are shown in [Tab. 2]. Each column heading shows first the radix and then the residue and divisor bits used to estimate the quotient digit for that test. The same heading convention will be followed for all of the results tables.
8:7x7 8: 6x6 8: 5x5 8: 4x4 8:3x3
basic operations 800,000 800,000 800,000 800,000 800,000
quot. adjustments 0 0 0 1,292 9,412
adjustments (%) 0 0 0 0.158 1.085
correction cycles 0 19 699 16,395 66,862
corrections (%) 0 0.002 0.087 2.049 8.357
bits per cycle 3.000 3.000 2.997 2.940 2.769
performance 1.000 1.000 0.999 0.980 0.923
Quotient carry distance 0 1 2 6 6
Table 2. Radix-8 division, with varying look-up table sizes. Small errors in the digit estimation show up in the 'quotient adjustments' which refine the prior quotient, but do not affect the residue or the speed. Larger errors manifest themselves as 'correction cycles' which modify the existing quotient and residue, and do slow the operation. In this table, the 'quotient adjustments' count only the adjustments which affect more than the least-significant quotient digit; we Page 9 may expect every correction to alter this digit but count only those which spill into more significant digits. In no case does the quotient carry propagate over more than 2 digits (6 bits). Whereas the largest, 7x7, table is able to predict a correct digit every time, the 6x6 table is inadequate by normal standards because it gives a few estimates which require correction. Even so it delivers a performance almost identical to the larger table (actually 2.99993 bits per cycle). The 5x5 and 4x4 tables are even less acceptable by normal criteria, with error rates of 0.1% and 2%, but here they still give performance within 0.1% and 2% of the optimal 3 bits per cycle. Even the minimal 3x3 table still yields the correct quotient digit 92% of the time and needs a correction cycle on only 8% of the steps, yielding nearly 2.77 bits per cycle. Comparative results for different radices are given later in [Fig. 3] (showing bits per cycle) and in [Fig. 4] (showing relative performance). These figures include all of the significant and useful cases to be discussed and should be consulted for quick comparisons. 8 Effect of table aspect ratio
Although Knuth implies that it is better to examine more residue digits than divisor digits, Atkins shows in his analysis that it is desirable to examine about the same number of bits from each value, or perhaps a few more bits from the divisor. We next examine the effect of trading off residue bits against divisor bits, in all cases keeping constant the total number of tested bits. The results of [Tab. 3] are for the '5x5' table of the previous section, but similar results were obtained for other configurations. For the present situation, where we are concerned only with obtaining a good estimate rather than the accurate value, it seems best to consider about the same number of bits from the two operands. Where the total number of bits is odd, the extra bit should be allocated to the residue. Results for the rest of the paper will mostly assume a 'square' table, without further justification.
8:6x4 8: 5x5 8: 4x6
basic operations 800,000 800,000 800,000
quot. adjustments 132 0 0
adjustments (%) 0.016 0 0
correction cycles 6,844 699 5,486
corrections (%) 0.856 0.087 0.685
bits per cycle 2.975 2.997 2.980
performance 0.992 0.999 0.993
Quotient carry distance 6 2 3
Table 3. Radix-8 division, varying table aspect ratio.
Page 10
9 Radix-16 division (4 bits per cycle)
We repeat the above work for radix-16 division. Again, it is not difficult to get close to the ideal performance of 4 quotient bits per cycle. We now show four look-up tables, examining 7, 6, 5 and 4 bits of the residue and divisor. Atkins requires a 7x9 table for radix 16, which is larger than even the largest of the tables used here. The change in radix reduces the number of 'basic operations' to 600,000, (6 digits for a 24 bit operand) compared with 800,000 for radix-8 operation (8 digits for 24 bits). Once again the larger tables give very nearly the maximum performance, with the 5x5 table within 1.5% of the ideal and even the 4x4 table (which considers only a single digit of each operand) only 8% off the possible speed. Quotient adjustments are again needed for the smaller tables, but even the smallest table never modifies more than 8 quotient bits (the current digit and its predecessor).
16: 7x7 16: 6x6 16: 5x5 16: 4x4
basic operations 600,000 600,000 600,000 600,000
quot. adjustments 0 0 250 2,854
adjustments (%) 0 0 0.041 0.442
correction cycles 57 615 8,489 46,507
corrections (%) 0.009 0.102 1.415 7.751
bits per cycle 4.000 3.996 3.944 3.712
performance 1.000 0.999 0.986 0.928
Quotient carry distance 1 3 7 8
Table 4. Radix-16 division, with varying look-up table sizes. 10 Radix-64 and radix-256 dividers
For division with higher radices, we initially assume that all multiples are available and observe the effect of only the reduced digit-estimation logic. Actually not much extra hardware is needed to handle radix-64 and even radix-256 division - we certainly do not need an adder input for each possible power of two. By using Booth recoding of the quotient digit we can handle radix-64 with a 3-input adder for the divisor multiples and radix-256 with a 4-input adder. Later we reduce the range of multiples to allow simplified divisor-multiple generation logic. We retain the earlier sizes of look-up table as covering a reasonable range of practical sizes. Although we assume the full range of divisor multiples for radix-64, we retain estimation logic which is quite small compared with Atkins predictions (9x 11 for radix 64). Particularly in the first two cases, 7x7 and 6x6 tables, we see from [Tab. 5] that the new algorithm largely absorbs any deficiencies of the digit estimation. The performance deteriorates markedly for the 5x5 and 4x4 tables, to the point where these are probably not worth considering, in comparison with the restricted Page 11 cases later.
64: 7x7 64: 6x6 64: 5x5 64: 4x4
basic operations 400,000 400,000 400,000 400,000
quot. adjustments 6 490 1746 0
adjustments (%) 0 0.114 0.330 0
correction cycles 3,492 29,744 128,667 382,634
corrections (%) 0.873 7.436 32.167 95.659
bits per cycle 5.948 5.585 4.540 3.067
performance 0.991 0.931 0.757 0.511
Quotient carry distance 9 12 11 6
Table 5. Radix-64 division - full multiples.Repeating the exercise for radix-256, we obtain the results of [Tab. 6]. The relatively poor quality of the digit estimates is even more noticeable here, but even so by examining just a single digit (8 bits) of the residue and divisor we achieve nearly 7.5 bits per cycle.
256: 8x8 256: 8x7 256: 7x7 256: 6x6 256: 5x5
basic operations 300,000 300,000 300,000 300,000 300,000
quot. adjustments 64 558 276 0 0
adjustments (%) 0.019 0.157 0.071 0 0
correction cycles 20,247 56,402 90,815 288,049 882,365
corrections (%) 6.749 18.80 30.27 96.02 294.1
bits per cycle 7.494 6.734 6.141 4.081 2.030
performance 0.937 0.842 0.768 0.510 0.254
Quotient carry distance 13 16 14 8 8
Table 6. Radix-256 division - full multiples.By comparing this table with the previous one, we see that the performance is largely determined by the unexamined bits of the most-significant digit. Thus examining a complete digit (6 or 8 bits respectively for radix-64 and radix-256) gives about 93% of the ideal performance, one bit less (5 or 7 bits) gives 75% and 2 bits less 51%. Nevertheless, it is interesting that reasonable performance is still possible if the estimation logic examines only part of the most-significant digits of the residue and divisor. As a more general observation, the algorithm is robust with respect to changes in the digit prediction logic. A poor prediction does not impair the final result, but may delay achieving that result. Practically though, it is clear that operation with a radix of 256 is not really satisfactory, at least with the size of look-up table which is used. With a 7x7 table, the performance is very little better than that of a radix-64 divider (6.14 bits, compared with 5.95). The benefit of the higher radix barely offsets the penalty of examining partial digits. Page 12 11 Division with few multiples available.
Divisor multiples can be divided into 3 categories -
16 7x7 16 6x6 16 5x5 16 4x4
basic operations 600,000 600,000 600,000 600,000
quot. adjustments 0 0 174 4,124
adjustments (%) 0 0 0.027 0.604
correction cycles 22,151 22,725 34,207 82,868
corrections (%) 3.692 3.788 5.701 13.811
bits per cycle 3.858 3.854 3.784 3.515
performance 0.964 0.964 0.946 0.879
Quotient carry distance 2 2 5 8
Table 7. Radix-16 division, with limitation to 'simple' multiples. Initially we examine radix-16, even though a 2-input adder is adequate to form all of the multiples with Booth recoding of the quotient digits. The estimation tables do not use Booth recoding but are just recoded versions of the previous ones with, for example, 11 being rounded to 10 or 12. As expected, there is some performance degradation as compared with the previous case where all multiples were assumed to be available. However even the simplest case still delivers over 3.5 bits per cycle. The speed is better than we would expect from noting that 1/8 of the multiples are unavailable and must be simulated; about half of these cases are just absorbed into the general operation and do not require explicit correction cycles. For higher radices it is especially useful to avoid a complete suite
of divisor multiples. We still restrict ourselves to simple multiples
of the form
Page 13
64: 7x7 64: 6x6 64: 5x5 64: 4x4
basic operations 400,000 400,000 400,000 400,000
quot. adjustments 10 736 1,482 0
adjustments (%) 0.002 0.143 0.250 0
correction cycles 91,476 116,488 193,466 412,402
corrections (%) 22.87 29.12 48.37 103.1
bits per cycle 4.883 4.647 4.044 2.954
performance 0.814 0.775 0.674 0.492
Quotient carry distance 6 12 11 6
single corrections 91,448 111,560 140,974 147,143
double corrections 14 2,464 26,246 85,618
> double corrections 0 0 0 30,116
Table 8. Radix-64 division, with limitation to simple multiples.
256: 8x8 256: 7x7 256: 6x6
basic operations 300,000 300,000 300,000
quot. adjustments 74 128 0
adjustments (%) 0.015 0.023 0
correction cycles 187,415 245,222 399,179
corrections (%) 62.47 81.74 133.1
bits per cycle 4.924 4.402 3.433
performance 0.616 0.550 0.429
Quotient carry distance 9 9 8
single corrections 173,975 152,214 112,568
double corrections 6,810 46,360 85,170
> double corrections 0 96 36,544
Table 9. Radix-256 division, with limitation to simple multiples.The results in [Tab. 8] and [Tab. 9] are extended to show details of the corrections. Radix-64 division is quite successful, generating an average of nearly 5 bits per cycle with either of the two larger tables. However the smallest table (4x4) is actually inferior to radix-16 with the same table size. The radix-256 results are inferior to the radix-64 results, showing the effect of having relatively fewer multiples available and having to rely much more on correction cycles. With radix-16, restricted multiples cover 7/8 or 87.5% of the total range of multiples. With radix-64 only 33 multiples are available (51.6% coverage), but only a single correction cycle is ever needed in most cases. Radix-256 uses 58 multiples (22.6%) and the sparse coverage requires many more correction cycles even with the larger tables. (Both radix-64 and radix-256 actually use occasional multiples of 66, 68, 258 Page 14 and 260, which are available without penalty or extra hardware given that 64 and 256 are provided.) While radix-64 operation is acceptable, there is clearly no benefit in using this method for a radix-256 divider. 12 The effect of using only shifted values as multiples
As an extreme restriction on the available multiples, we can restrict them to just powers of 2 (those which are available by shifting). We retain the original style of lookup tables, even though they are clearly inappropriate in this case; we should be able to achieve comparable performance with much simpler quotient estimation.
64: 7x7 64: 6x6 64: 5x5 256:7x7
basic operations 400,000 400,000 400,000 300,000
quot. adjustments 0 0 0 0
adjustments (%) 0 0 0 0
corrections 407,228 428,667 484,1 62 554,306
corrections (%) 101.8 107.2 121.0 184.8
bits per cycle 2.973 2.896 2.714 2.809
performance 0.496 0.483 0.452 0.351
Quotient carry distance 5 5 5 9
Table 10. Radix-64 and radix-256 division, limited to power-of-2
multiples.The division should tend to be equivalent to a variable shift length
algorithm, with multiples of 13 Graphical summary of results
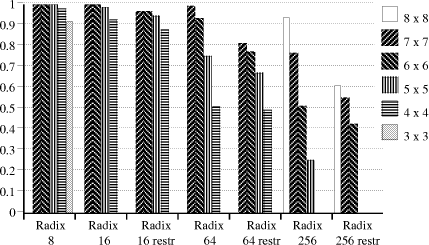
In [Fig. 3] and [Fig. 4] we show the performance results for the
various radices and sizes of look-up table. Figure 3 shows the average
quotient bits delivered per cycle, while Figure 4 shows the
performance for each radix, with 100% being N bits/cycle for a radix
of
Page 15
Figure 3. Average bits/cycle, for different radices and table sizes
Figure 4. Relative performance, for different radices and table sizes The graphs show quite clearly that a table should work with about 1 digit for each input; a 6x6 table for example gives negligible benefit on a radix-16 divider, but with radix-256 gives fewer bits per cycle that with radix-64. This will be mentioned again later, in connection with some other recent work. 14 Generation of the quotient digits
The present paper has generated quotient digits only from look up tables addressed
Page 16 by the high order digits of the residue and divisor. This technique might not be the best one and in that regard the current work should be regarded more as a feasibility study of the new technique. The usual problem in division is that the critical path consists of the generation of the quotient digit, then the generation of the corresponding divisor multiple and finally the addition/subtraction, in other words all of the difficult operations! [Montuschi and Ciminiera 1994] point out indeed that many methods of 'improving' division really do little more than move the dominant delay around the critical path! Nevertheless there are several ways of accelerating the digit estimation.
It is not easy to predict which is the best method. Most of the table-lookup methods insert extra delay into the division cycle and slow down every cycle; they may be better if there is spare time in each cycle. The prescaling methods however allow faster cycles within the division proper, but require additional steps for the preliminary adjustments and may be better where the system clock matches the critical path delay within the division logic. 15 Other recent work
A very recent paper (published since this paper was submitted) presents some very similar techniques [Cortadella and Lang, 1994]. A comparison of the two methods is conveniently presented as a series of points (with references to 'this paper' and 'their paper' having the obvious meanings).
The two papers present different approaches to the same problem, both illustrating that high-radix division does not require exact high precision quotient-digit estimates.
We have shown that it is possible to obtain satisfactory high-radix division, even when the division process is subject to one of two significant restrictions -
The tests indicate that the new techniques are appropriate for radices up to 64, but less satisfactory with a radix of 256, largely because of restrictions on the digit-estimation logic and the number of divisor multiples which are available. If we have a multiplier which is designed for, say, radix-64 multiplication, its hardware can be used as the basis of a divider with nominal radix-64 operation. This paper shows that, with relatively simple digit estimation logic, it is easy to achieve, if not the full 6 bits per cycle, then certainly 4 or 5 bits.
The lookup tables are generated as a simple function of the high-order residue and divisor bits, assumed to index the rows and columns respectively of the table. The process is parametrised to facilitate the generation of tables of differing sizes and shapes, and for differing radices. The tables are generated for positive residue and divisor (with the most-significant divisor bit always 1) and the negative half then generated as the complement of the positive half. There is evidence that minor improvements might be possible by fine-tuning some table entries in particular cases but that has mot been attempted. The basic parameters are
From these are derived several other values
Logically, the table rows extend from -maxRow to maxRow - 1, and the columns from minCol to maxCol - 1. We calculate also a scaling factor chosen to give an intermediate result of twice the true estimate. A mapping table then rounds the intermediate result of twice the true estimate. A mapping table then rounds the intermediate value to the correct estimate, or rounds with suppression of complex multiples. Page 20 The essential loops for producing the table are then
for (col = minCol; col <= maxCol; col++)
for (row = 0; row <= maxRow; row++)
Table[row + maxRow][col - minCol] = (beta * row) / col;
For operation with less than the full set of divisor multiples the table values are rounded to the nearest available multiple.
References
[Atkins 1970] D.E. Atkins, "Higher-Radix Division Using Estimates of the Divisor and Partial Remainders", IEEE Trans. Comp., August 1970, pp 720-733 [Cortadella and Lang, 1994] J. Cortadella and T. Lang, "High-Radix Division and Square Root with Speculation", IEEE Trans. Comp., August 1994, pp 919-931 [Ercegovac, Lang and Montuschi 1993] M.D. Ercegovac, T. Lang, P. Montuschi, "Very High Radix Division with Selection by Rounding and Prescaling", Proc. Eleventh IEEE Symp. Comp. Arithmetic, 1993, pp 112-119 [Freiman 1961] C.V. Freiman, "Statistical Analysis of Certain Binary Division Algorithms", Proc. IRE, Vol 49, No 1, Jan 1961, pp 91-103 [Hwang 1979] K. Hwang, "Computer Arithmetic: principles, architecture and design", John Wiley and Sons, New York, 1979 [Flores 1963] Ivan Flores, "The Logic of Computer Arithmetic", Prentice-Hall, Englewood Cliffs, 1963 [Kawahito et al 1994] S. Kawahito, M. Ishida, T. Nakamura, M. Kamyama, T. Higuchi, "High-Speed Area-Efficient Multiplier Design Using Multiple-Valued Current-Mode Circuits", IEEE Trans Comp., Vol 43, No 1, Jan 1994, pp 34-42 [Knuth 1969] D.E. Knuth,"The Art of Computer Programming", Vol 2 Seminumerical Algorithms, Addison Wesley 1969 [MacSorley 1961] O.L. MacSorley,"High Speed Arithmetic in Binary Computers", Proc. IRE, Vol 49, Jan 1961, pp 67-91 [Montuschi and Ciminiera 1994] P. Montuschi and L. Ciminiera, "Over-Redundant Digit Sets and the Design of Digit-By-Digit Division Units", IEEE Trans. Comp., Vol 43, No 3, March 1994, pp 269-277 [Robertson 1958] J.E. Robertson, "A New Class of Digital Division Methods", IEEE Trans. Comp., Vol C-7, No 8, September 1958, pp 218-222 [Svoboda 1963] A. Svoboda, "An Algorithm for Division", Information Proc Machines, Vol 9, pp 25-32, 1963 Page 21 [Schwarz and Flynn 1993] E.M. Schwarz, M.J. Flynn, "Parallel High-Radix Nonrestoring Division", IEEE Trans. Comp., Vol 42, No 10, Oct 1993, pp 1234-1246 [Tocher 1956] K.D. Tocher, "Techniques of Multiplication and Division for Automatic Binary Computers", Q. J. Mech. Appl. Math. Vol 11 Pt 3 pp 364-384 [Wallace 1964] C.S. Wallace, "A Suggestion for a Fast Multiplier", IEEE Trans. Elec. Comp., Vol EC-13, Feb 1964, pp 14-17 [Waser and Flynn 1982] S. Waser, M.J. Flynn, "Introduction to Arithmetic for Digital Systems Designers", Holt, Reinhart and Winston New Yoerk, 1982 [Wilson and Ledley 1961] J.B. Wilson, R.S. Ledley,"An Algorithm for Rapid Binary Division", IRE Trans. Elec. Comp. Vol EC-10, Dec 1961, pp 662-670 [Wong and Flynn 1992] D. Wong, M. Flynn, "Fast Division Using Accurate Quotient Approximations to Reduce the Number of Iterations", IEEE Trans. Comp., Vol 41, No 8, Aug 1992, pp 981-995 Page 22
|
|||||||||||||||||
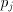= the residue used in the j-th cycle,
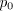= the initial dividend,
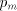= the remainder, and
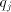= the j-th quotient digit
We also have that 
= the radix, eg 2, 4, 8, 16,
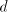= the divisor, and
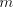= the number of radix-r digits in the quotient
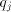) of the divisor
from the residue and enter the same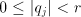 
, this ensuring that a properly
chosen value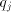 
will eliminate a digit of 
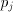and ensure that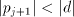 
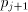is in the range to allow the iteration to proceed. The
crux of most division methods lies in generating the correct value of
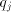so that the residue is properly reduced and the generated digit is
accurate. For high radices this may require considerable logic; so
much so that Waser and Flynn consider that SRT algorithms are
unsuitable for any radix greater than 4.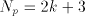
or 
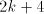, and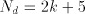
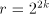
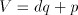. The value is unchanged if we put 
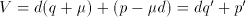. In other words we can add any quantity
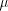to the quotient, provided that we also subtract 
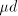from the
residue. A quotient digit can be formed as a result of several
operations with the same operand alignment; if the estimation logic
gives a poor estimate of the quotient digit, we can 'hold' that division
cycle and correct or refine the estimate until the residue is within
range for the next reduction.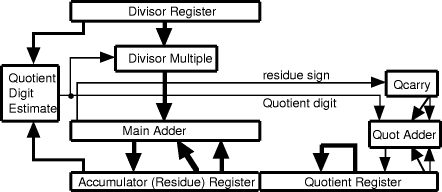
.
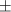1, shifting over strings of 0s and
1s. Variable shift algorithms are known to have an asymptotic
performance of about 3 bits per cycle (2.5 - 3.5, see [
. Results are shown for only the more realistic cases of full
multiples and restricted multiples. Results for corrections and
quotient adjustments are not presented; they are essentially internal
or intermediary phenomena whose consequences are apparent in the final
performance.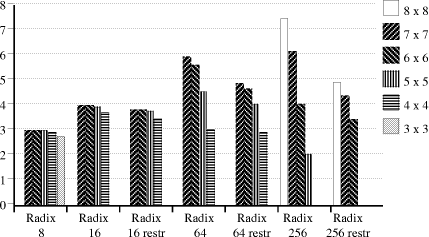
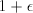, where 
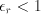. At the same time they apply similar
transformations to the dividend; effectively they multiply the divisor
and dividend by the same factor, leaving the quotient unchanged. With
the divisor of that form, the high order digits of the residue are
precisely the desired quotient digit. Without recoding the divisor
digits we may expact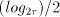 
iterations to reduce the divisor and the same
number of parallel operations to transform the dividend, giving a
total of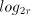 
preliminary operations. The cost of these operations would
have to be offset against the reduction in the cycle time from the
improvement in the time to generate quotient digits. A problem is that
it does not yield a remainder.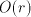
, rather
than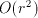
. Conversion from the difference back to the actual digit
estimate will require logic of similar scale to produce the
antilog. Depending upon the logic family, the complex of 3 small
tables (or equivalent) will certainly be simpler and may be faster
than the single large lookup table. Note that we do not require wholly
accurate digit estimates.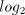
integral
bits. Thus radix-16 requires a logarithm of the form xx.xxxx, and
radix-256 of the form xxx.xxxxxxxx. The detailed results are slightly
different from those for the direct look-up tables, even though the
formulae are nominally equivalent. In some cases there is a slight
degradation in performance but many cases improve by 1 - 2%. This
demonstrates both the robustness of the algorithm with respect to
slight changes in the digit estimates and the possibility of improving
the performance in particular cases by fine tuning the digit
estimation.
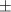1, but does
not explore the consequences of possible quotient carry propagation.
