| Submission Procedure |
Using Program Checking to Ensure the Correctness of Compiler ImplementationsSabine Glesner Abstract: We evaluate the use of program checking to ensure the correctness of compiler implementations. Our contributions in this paper are threefold: Firstly, we extend the classical notion of black-box program checking to program checking with certificates. Our checking approach with certificates relies on the observation that the correctness of solutions of NP-complete problems can be checked in polynomial time whereas their computation itself is believed to be much harder. Our second contribution is the application of program checking with certificates to optimizing compiler backends, in particular code generators, thus answering the open question of how program checking for such compiler backends can be achieved. In particular, we state a checking algorithm for code generation based on bottom-up rewrite systems from static single assignment representations. We have implemented this algorithm in a checker for a code generator used in an industrial project. Our last contribution in this paper is an integrated view on all compiler passes, in particular a comparison between frontend and backend phases, with respect to the applicable methods of program checking. Key Words: compiler, implementation correctness, program checking, certificates, compiler architecture, compiler generators, code generation Category: D.3.4, D.2.4, F.3.1, F.4.2 1 IntroductionCompiler correctness is a necessary prerequisite to ensure software correctness and reliability as most modern software is written in higher programming languages and needs to be translated into native machine code. In this paper, we address the problem of implementing compilers correctly. Recently, program checking has been proposed as a method to achieve this goal. Program checking has been successfully applied to compiler frontends while its application to compiler backends has remained as an open problem. We close this gap. Therefore we propose a novel checking method which we call program checking with certificates. It is particularly suited for checking the results of optimization problems. We have applied program checking with certificates to code generation, a phase in optimizing compilers which transforms intermediate representations into machine code. In this paper, we present our checking algorithm for such code generators as well as a case study with experimental results proving the practicality of our approach. Moreover, we summarize previous work about frontend checking and compare it with our insights concerning backend checking. Page 191 Thereby we reveal significant differences between the computations and corresponding checking tasks in compiler frontends and backends. With this evaluation, we achieve an integrated view an all compiler passes concerning the respectively applicable checking methods and the advantage they might or might not offer compared to the full verification of the respective entire compiler passes. Program checking is based on the observation that if one wants to obtain provably correct results, it is sufficient to verify the results instead of verifying the program code that produced them. Such a strategy makes sense whenever it is much more expensive to compute a result than to check a result. Compiler frontend computations have typically unique solutions. Even though calculating them might involve complex computations, their correctness can nevertheless be checked easily. Hence, for frontend computations, the standard black-box checking method as proposed in [Blum et al. 1993, Blum and Kannan 1995] can be applied. In backends, the situation is different because complex optimization problems need to be solved which might have much more than one solution. When checking the correctness of the solution of such an optimization problem, it does not matter if it is optimal, thus simplifying the checking task and the verification of the checker considerably. Many of the backend problems are NP-hard. Such problems are characterized by the fact that the correctness of a solution can be shown by a proof of polynomial length. Our proposed method of program checking with certificates uses this property. We extend the checking scenario by requiring that the implementation to be checked also outputs a certificate which tells the checker how the solution has been computed. The checker uses this certificate to recompute the solution. It classifies the solution of the implementation as correct only if it is identical with the recomputed solution. Even though compilers are often assumed to be error free and trustworthy, many compilers used in practice do have bugs. This leads in turn to the phenomenon that many programmers try to find bugs in their own code rather than assuming mistakes in the compilers which they use. Nevertheless compilers are not above suspicion as is demonstrated by the bug reports of widely-used compilers [Borland/Inprise 2002a, Borland/Inprise 2002b]. Often compilers work correctly as long as no special optimizations are used. But as soon as higher optimization levels are switched on, errors occur, cf. e.g. [Newsticker 2001] which describes an error in Intel's C++ compiler showing up during interprocedural optimization (option -ipo). This paper focuses on the question of how compilers can be implemented correctly. Besides this question there are two other aspects of correctness. Firstly one needs to prove that the specification of the compiler implementation is correct. Such a proof requires the certificate that the semantics of the respecting source and translated target programs are the same. Page 192 Secondly, one needs to take into account that the compiler implementation is typically written in a higher programming language and needs to be translated into machine code itself. Hence, it is necessary to guarantee that the compiler implementation is compiled correctly into machine code. These different aspects of compiler correctness as well as related work dealing with them are summarized in section 2. In section 3, we introduce our method of program checking with certificates which can be used to check the correctness of the solutions of optimization problems. Moreover, we argue why we cannot hope to get a similar method to also check the optimality of the computed solutions. In section 4, we discuss the characteristics of compilers, in particular their structure and the corresponding implications for the task of correctness checking. Sections 5 and 6 present our novel work on backend checking. In section 5 we apply program checking with certificates to compiler backends by proposing a checking algorithm for the code generation phase. Thereby we take the code generator generator CGGG (code generator generator based on graphs) [Boesler 1998] as basis for our investigations. It implements bottom-up rewrite systems (BURS) [Nymeyer and Katoen 1997]. We modified it so that the code generators geneated with it do not only produce the target program but a certificate as well. Moreover, we argue that the checkers can be generated from specifications in the same way as the code generators. In section 6 we show how program checking with certificates behaves in practice. In our case study, we have implemented a checker for an industrial compiler backend generated with the CGGG system. In section 7 we restate related work about frontend checking with respect to the characteristics established in section 4. In section 8, we evaluate frontend and backend checkers in an integrated view. In section 9, we discuss related work. Finally we close with conclusions and aspects of future work in section 10. 2 Compiler CorrectnessCompiler correctness is widely accepted as an important requirement and many different definitions exist. In this section, we summarize the definition given in [Goos and Zimmermann 1999, Goos and Zimmermann 2000] because it has two main advantages: Firstly, it considers resource limitations which might cause compiler errors. Secondly, it clearly distinguishes between specification, implementation, and compiler compilation correctness. In particular, it offers a solution to the problem that one might wish to use compiler generators whose verification itself would be too expensive. Earlier work on compiler verification [Polak 1981, Chirica and Martin 1986] also distinguished between specification and implementation correctness but did not mention the problem that the translation of a verified compiler implementation into executable machine code also needs to be verified, i.e. the question of compiler compilation correctness. [Polak 1981] mentioned the problem of compiler generators but did not offer any solution. Moreover, [Polak 1981] addressed the question of resource limitations and stated a definition similar to the one described below. Page 193 Preservation of Observable Behavior A correct compiler is required to preserve the semantics of the translated programs. More precisely, it should preserve their observable behavior. This requirement has been discussed extensively. In a curtailed summary, the definition of [Goos and Zimmermann 1999, Goos and Zimmermann 2000] states that the execution of a program can be represented by an operational semantics as a sequence of states. Selected observable states communicate with the outside world. A translation is correct iff for each source and translated target program and for each possible program input, the sequence of observable states is the same. Resource Limitations This definition raises the question of resource limitations. In a mathematical sense, each compiler will produce no result for nearly all programs, namely all those that do not fit into the memory of the computer on which the compiler is running. In the same sense, each translated program will produce no result for nearly all inputs, namely those inputs that are too long to fit into the memory of the computer executing the translated program. This question can be carried to extremes by asking whether a compiler is correct that never produces any target program but only says for each source program that there is no result due to resource limitations. In a practical sense, such a compiler is worthless. But from a formal point of view, it is correct. Since nearly all programs and program inputs, resp., do not fit into the memory of any existing computer, we cannot hope for a better formal definition. From a practical perspective, we require a correct compiler to translate most programs of reasonable length such that their observable behavior is preserved for most inputs of realistic interest. Decomposition along Compiler Passes Each compiler consists of a sequence of translation steps (cf. section 4 for more details), also called compiler passes. Each compiler pass is defined by a translation specification. To ensure the correctness of the overall translation, it is sufficient to prove that each individual translation step preserves the semantics of the translated programs. Correctness of Compiler Specification The correctness proof for each individual compiler pass can be split into three different proof obligations. The first concerns the specification correctness. Thereby it is necessary to show that the specified translation preserves the semantics of the source programs, i.e. retains their observable behavior. In [Zimmermann and Gaul 1997], such a translation verification has been done for all compiler passes from a simple imperative source language into DEC-Alpha machine code. Such correctness proofs can also be done mechanically by using automated theorem provers [Dold et al. 1998]. Page 194 Correctness of Compiler Implementation The second level of compiler correctness is concerned with the implementation correctness, i.e. the question of how the translation specification can be implemented correctly. Thereby one needs to take into account that today's compilers are not written by hand but rather generated from specifications. It would imply an enormous and much too expensive effort if one wanted to verify either the generator implementation itself or the compilers produced by them. The solution to this dilemma is program checking [Goerigk et al. 1998]. Instead of verifying generator or generated compiler, one verifies the correctness of the result of the generated compiler, i.e. the target program. This has been done successfully for the frontends of compilers [Heberle et al. 1999]. To guarantee the formal correctness of the result, it is still necessary to verify the checker code formally. Since most search and optimization problems in the area of compiler construction are much more expensive to solve than to check, this verification task can be done much faster. Correctness of Compiler Compilation Finally, there is the question of encoding correctness. Compiler and checker are typically written in a higher programming language and need to be translated into machine code themselves. For this purpose one needs an initial correct compiler. The investigations in [Dold et al. 2002, Dold and Vialard 2001] show that it is possible to fully verify a non-optimizing compiler mechanically by using an automated theorem prover. Focus of this Paper In this paper, we concentrate on implementation correctness, in particular on the implementation correctness of optimizing backends. Therefore, we extend the classical notion of program checking and introduce program checking with certificates. This checking method is particularly suited to check the results of optimizations, as for example the target programs produced by optimizing compiler backends. Thus, we solve the open question of how compiler backend checking can be done successfully. Moreover, we compare the frontend and backend tasks in a compiler and identify principal differences between the corresponding checking tasks. This comparison gives us an integrated view on all compiler passes and the checking methods applicable in the respective phases. 3 Program Checking: Trust is Good, Control is Better!In this section, we introduce the notion of program checking with certificates. With it, we extend the well-known concept of black-box program checking presented in [Blum and Kannan 1995]. Black-box program checking assumes that an implementation solving a certain problem is used as a black box and that an independent checker examines if a particular result is correct. Page 195 We summarize this approach in subsection 3.1. In subsection 3.2, we show how it can be extended to be applicable in the context of optimization problems which might not have only a single but possibly several correct solutions. In subsection 3.3, we argue why it is unlikely that we might be able to construct efficient checkers for the optimality of a solution. 3.1 Black Box Program CheckingProgram checking [Blum and Kannan 1995] has been introduced as a method to improve the reliability of programs. It assumes that there exists a black box implementation P computing a function f. A program result checker for f checks for a particular input x if P (x) = f(x). Assume that f : X -> Y maps from X to Y . Then the checker checker has two inputs, x and y, whereby x is the same input as the input of the implementation P and y is its result on input x. The checker has an auxiliary function f_ok that takes x and y as inputs and checks whether y = f(x) holds. proc checker (x : X, y : Y
) : BOOL Note that the checker does not depend on the implementation P.
Hence, it can be used for any program Page 196
Figure 1: Computation Spaces in NP 3.2 Program Checking with CertificatesWe introduce the method of program checking with certificates by extending the notion of a program result checker such that it is allowed to observe the implementation program P during its computation of the result. In our setting, the program P might tell the checker how it has computed its solution. To motivate this idea theoretically, let us take a look at the common
definition for problems in NP. NP is the union of all problems
that can be solved by a nondeterministic polynomial time Turing machine.
An alternative equivalent definition for NP states the following:
Assume that a language L is in NP. Then there exists a polynomial
time Turing machine M such that for all x When solving optimization problems, as e.g. in the backends of compilers, huge search spaces need to be searched for an optimal or at least acceptable solution. When we want to check the correctness of the solution, we do not care about its optimality, only about its correctness. Hence, we can use the certificate to recompute the result. Page 197 Figure 2: Checker Scenario with Certificates In particular for the optimization variants of NP-complete problems, we have the well-founded hope that the checker code is much easier to implement and verify than the code generator itself. Our checking scenario with certificates is summarized in figure 2. In the case of simple checking tasks, the certificate input for the checker is empty, i.e. does not exist. But what if the implementation is malicious and gives us a buggy certificate? The answer is simple: If the checker manages to compute a correct solution with this erroneous certificate and if, furthermore, this correct solution is identical with the solution of the implementation, then the checker has managed to verify the correctness of the computed solution. It does not matter how the implementation has computed the solution or the certificate as long as the checker is able to reconstruct the solution via its verified implementation. The checker functionality can be described as follows. Let P
be the implementation of a function f with input x proc checker (x : X, y : Y,
Certificate) : BOOL NP-complete problems have the tendency to have very natural certificates. This holds in particular for the NP-complete problems to be solved in compiler backends, cf. section 5. 3.3 What About Checking the Optimality of Solutions?Our notion of checking with certificates makes sure that a solution is correct but does not consider checking its quality. In this section, we want to argue that due to certain widely-accepted assumptions in complexity theory, we cannot hope to construct efficient checkers which check if a solution is optimal. Page 198 Problems in NP are always decision problems, asking if a certain instance belongs to a given language (e.g.: Is this a Hamiltonian path? Does the traveling salesman have a tour of at most length n?). These problems are characterized by their property that each positive instance has a proof of polynomial length, a certificate. E.g. the Hamiltonian path itself or a tour for the traveling salesman of length n or smaller would be such certificates. Conversely, the class coNP is defined as containing all those languages whose negative instances have a proof of non-membership, a disqualification, of polynomial length. E.g. the language containing all valid propositional formulas is such a language. A non-satisfying assignment for a formula proves that this formula does not belong to the language of valid formulas. Hence, this non-satisfying assignment is a disqualification. To prove that a solution is not only correct but also optimal, one would need a positive proof in the spirit of NP-proofs and a negative proof as in the case of coNP-proofs. The positive proof states that there is a solution at least as good as the specified one. The negative proof would state that there is no better solution. Complexity theory [Papadimitriou 1994] has studied this situation and defined the class DP. DP is the set of all languages that are the intersection of a language in NP and a language in coNP. One can think of DP as the class of all languages that can be decided by a Turing machine allowed to ask a satisfiability oracle twice. This machine accepts iff the first answer was `yes' (e.g. stating that the optimal solution is at least as good as the specified one) and the second `no' (stating that the optimal solution is at most as good as the specified one). It is a very hard question to decide whether an optimization problem lies in DP. The current belief in complexity theory is that NP-complete problems are not contained in coNP, implying that conceivably they do not have polynomial disqualifications. So if we design a checker for a problem being at least NP-complete, it does not surprise that we are not able to announce a polynomial checker also for the optimality of a solution, since such an announcement would solve a few very interesting questions in complexity theory. 4 Compiler ArchitectureCompilers consist of two main parts, their frontend and their backend. Both parts can be specified by theoretically well-founded methods. Moreover, these methods can be implemented in generators. Yet, there is a fundamental difference between the frontend and backend tasks. In subsection 4.1 we describe the standard compiler architecture and the methods used to specify and generate the respective compiler parts. Then we proceed by discussing the fundamental differences between frontend and backend tasks in subsection 4.2. Page 199 4.1 Structure of CompilersCompilers consist of a frontend and of a backend. The frontend checks if a given input program belongs to the programming language and transforms it into an intermediate representation, cf. figure 3. The backend takes this intermediate representation, optimizes it, and generates machine code for it, cf. figure 5.
Figure 3: Frontend Tasks Frontend Tasks Programming languages are described and processed by a three-stage process: First, a regular language defines how to group individual characters of the input program into tokens. For example, the character sequence `e' `n' `d' would be combined into the token `END', treated as an indivisible unit. Regular languages can be implemented easily by finite automata, constituting the lexical analysis, also called scanner. These tokens are the basis to define the context-free structure of programs by a deterministic context-free grammar. For each program, this context-free grammar defines a derivation tree (the concrete syntax). Context-free languages can be implemented by pushdown automata. The corresponding compiler pass is called syntactic analysis or parser. These derivation trees and the corresponding context-free grammar can be simplified in many cases, e.g. by eliminating chain productions, yielding the abstract syntax used in all subsequent definitions. In the third stage of language definition, attributes are associated with the nodes in the abstract syntax tree, e.g. by specifying an attribute grammar. These attributes define the context-sensitive properties of programs. They are determined during the semantic analysis. In general, these attributes cannot be computed locally within the scope of one production but need more sophisticated strategies which traverse the abstract syntax tree in special orders. Based on the attributed abstract syntax tree, the intermediate representation of the program is easily computed. SSA Intermediate Representation Static single assignment (SSA) form has become the preferred intermediate program representation for handling all kinds of program analyses and optimizing program transformations prior to code generation [Cytron et al. 1989, Cytron et al. 1991, Cytron and Ferrante 1995]. Its main merits comprise the explicit representation of def-use-chains and, based on them, the ease by which further dataflow information can be derived. Page 200 Figure 4: SSA Example By definition SSA-form requires that a program and in particular each
basic block is represented as a directed graph of elementary operations
(jump, memory read/write, unary or binary operation) such that each ''variable''
is assigned exactly once in the program text. Only references to such variables
may appear as operands in operations. Thus, an operand explicitly indicates
the data dependency to its point of origin. The directed graph of an SSA-representation
is an overlay of the control flow and the data flow graph of the program.
A control node may depend on a value which forces control to conditionally
follow a selected path. Each block node has one or more such control nodes
as its predecessor. At entry to a basic block, As example, figure 4 shows the SSA representation for the program fragment: a := a+2; if(..) { a := a+2; } b := a+2
In the first basic block, the constant 2 is added to a. Then the cond
node passes control flow to the `then' or to the `next' block, depending
on the result of the comparison. In the `then' block, the constant
2 is added to the result of the previous add node. In the `next'
block, the Page 201
Figure 5: Backend Tasks Backend Tasks The backend takes the intermediate representation, optimizes it, and generates corresponding machine code, cf. figure 5. The machine-independent optimizations transform an SSA representation into a semantically equivalent SSA representation, thereby exploiting information from control and data flow analyses. Complete code generation involves several phases which depend on each other. Code selection and generation assigns machine instructions to the operations of the intermediate representation and produces a sequence of machine instructions. Register allocation decides which values of the intermediate representation are to be kept in registers and which need to be stored in memory. Instruction scheduling rearranges the code sequence computed during code selection in order to exploit the architecture of the target machine. All these problems are optimization problems. Many of them are NP-hard. The most prominent such example is register allocation which can be reduced to the problem of graph coloring known to be NP-complete. Code generation, on which we concentrate in sections 5 and 6, may be viewed as a rewrite process on the intermediate representation. In traditional cases this representation is a set of trees which are rewritten by techniques like Bottom Up Pattern Matchers (BUPM) [Emmelmann 1992, Emmelmann 1994] or Bottom Up Rewrite Systems (BURS) [Nymeyer and Katoen 1997]. Both mechanisms use rewrite rules: E.g. (+(r, c) -> r, code) is a rule to rewrite an addition of two operands by its result. The target code code for this rule is emitted simultaneously. In an SSA representation, the program is represented by a graph with explicit data and control flow dependencies. Therefore one needs graph rewrite systems when rewriting SSA graphs during code generation. There might be more than one rule for a given subtree or subgraph. Since rules are annotated with their costs, the cheapest solution needs to be determined by a potentially huge search. Page 202 Compiler Generators The translation methods for compilers mentioned in this subsection are all implemented in generators. There exists a variety of generators for the lexical and syntactic analysis, just to name the Unix tools Lex and Yacc as most prominent examples. They take regular expressions and LR(1) context-free grammars, resp., as input and generate the corresponding compiler passes. The semantic analysis can be generated based on miscellaneous mechanisms, e.g. based on attribute grammars [Eli 2003]. For the machine-independent optimizations, there is e.g. the PAG system [Martin 1998]. The BEG tool [Emmelmann et al. 1989] generates machine code by implementing bottom-up pattern matchers. In our case study, cf. section 6, we use the code generator generator CGGG [Boesler 1998]. It generates code generators that implement graph rewrite systems based on BURS theory [Nymeyer and Katoen 1997]. 4.2 Significant Difference between Frontends and BackendsThe frontend computations have one common characteristic: Their result is uniquely determined. This simplifies the check whether their result is correct. It can be done completely without any knowledge about the internal decisions of the compiler. In contrast, backend computations solve optimization problems. They have a huge solution space with potentially several solutions. Cost functions define their quality. When checking the solutions of backends, only the correctness of the solutions, not their optimality, needs to be checked. We do this by using internal knowledge about the decisions of the compiler. We call this internal knowledge certificate, as it corresponds directly with a correctness proof as discussed in subsection 3.2. Thus we restrict the search space and get more efficient checkers. Remark: In practical frontend construction, one faces the problem of constructing a deterministic context-free grammar which in addition needs to satisfy the special needs of the parser generator one might wish to use (e.g. parser generators accepting only LALR grammars). Such a grammar is not unique since a programming language might have ambiguities. When constructing a parser for one specific programming language, one must avoid and solve ambiguities and conflicts, e.g. when dealing with subtle precedence and associativity rules, by specifying a deterministic context-free grammar, i.e. a grammar which defines a unique syntax tree for each program. This grammar is not unique. Nevertheless, if such a grammar exists and has been constructed, the syntactic analysis will always produce a unique result. In the following two sections, we present our novel checking algorithm for the code generation phase as well as the experimental results of our case study implementing it. The checking algorithm is based on program checking with certificates. Afterwards we proceed by summarizing previous work on frontend checking. Page 203 Then we evaluate frontend and backend checkers with respect to two criteria: The first criterion is the question if formal correctness and verification can be established more easily via the checker approach than by verifying the compiler or compiler generator directly. The second criterion asks if the checkers can be generated in order to ensure their practical applicability for generated compilers. With this common evaluation of frontend and backend checkers, we achieve an integrated view on all compiler passes and the respective checking methods which are applicable for them. 5 Program Checking for Compiler BackendsThe backend of a compiler transforms the intermediate representation into target machine code. This task involves code selection, register allocation, and instruction scheduling, cf. subsection 4.1. These problems are optimization problems that do not have a unique solution but rather a variety of them, particularly distinguished by their quality. Many of these problems are NP-hard. Hence, algorithms for code generation are often search algorithms trying to find the optimal solution or at least a solution as good as possible with respect to certain time or space constraints. If one wants to prove the implementation correctness of such algorithms, it is not necessary to prove the quality of the computed solutions. It suffices to prove their correctness. 5.1 BURS and the CGGG SystemIn this paper, we deal with checking the code selection phase. Thereby we consider bottom-up rewrite systems (BURS) for code generation. BURS systems are a powerful method to generate target machine code from intermediate program representations. Conventional BURS systems allow for the specification of transformations between terms which are represented as trees. Rules associate tree patterns with a result pattern, a target-machine instruction, and a cost. If the tree pattern matches a subtree of the intermediate program representation, then this subtree can be replaced with the corresponding result pattern while simultaneously emitting the associated target-machine instruction. The code generation algorithm determines a sequence of rule applications which reduces the intermediate program tree into a single node by applying rules in a bottom-up order. Traditionally, BURS has been implemented by code generation algorithms which compute the costs of all possible rewrite sequences. This enormous computation effort has been improved by employing dynamic programming. The work by Nymeyer and Katoen [Nymeyer and Katoen 1997] enhances efficiency further on by coupling BURS with the heuristic search algorithm A*. This search algorithm is directed by a cost heuristic. It considers the already encountered part of costs for selected code as well as the estimated part of costs for code which has still to be generated. Page 204 A* is an optimally efficient search algorithm. No other optimal algorithm is guaranteed to expand fewer nodes than A*, cf. [Dechter and Pearl 1985]. Using such an informed search algorithm offers the advantage that only those costs need to be computed that might contribute to an optimal rewrite sequence. [Nymeyer and Katoen 1997] propose a two-pass algorithm to compute an optimal rewrite sequence for a given expression tree. The first bottom-up pass computes, for each node, the set of all possible local rewrite sequences, i.e. those rewrite sequences which might be applicable at that node. This pass is called decoration and the result is referred to as decorated tree. The second top-down pass trims these rewrite sequences by removing all those local rewrite sequences that do not contribute for the reduction of the term. BURS theory has been extended to be able to deal with SSA representations
by a two-stage process [Boesler 1998]. The first stage
concerns the extension from terms, i.e. trees, to terms with common subexpressions,
i.e. DAGs. This modification involves mostly technical details in the specification
and implementation of the rewrite rules. The second stage deals with the
extension from DAGs to potentially cyclic SSA graphs. SSA graphs might
contain data and control flow cycles. There are only two kinds of nodes
which might have backward edges, The BURS code generation algorithm has been implemented in the code generator generator system CGGG (code generator generator based on graphs) [Boesler 1998]. CGGG takes a specification consisting of BURS rewrite rules as input and generates a code generator which uses the BURS mechanism for rewriting SSA graphs, cf. figure 6. The produced code generators consist of three major parts. First the SSA graph is decorated by assigning each node the set of its local alternative rewrite sequences. Then the A*-search looks for the optimal solution, namely the cheapest rewrite sequence. This search starts at the final node of the SSA graph marking the end of computation, by working up through the SSA graph until the start node is reached. Finally, the target machine code is generated by applying the computed rewrite sequence. An example for a rule from a code generator specification is: RULE a:Add (b:Register b) > s:Shl (d:Register c:Const);
RESULT d := b;
EVAL { ATTR(c, value) = 1; }
EMIT {}
Page 205 Figure 6: Extended CGGG Architecture This rule describes an addition of two operands. On the left hand side of the rule, the first operand is a register with short name b. The second operand is the first operand again, identified by the short name. Note that the left-hand side of this rule is a directed acyclic graph. If the code generator finds this pattern in the graph, it rewrites it with the right-hand side of the rule. In general, this could be a DAG again. Thereby the EVAL code is executed. This code places the constant 1 in the attribute field value of the Const node. The RESULT instruction informs the register allocator that the register d equals register b. Optimal BURS code generation for SSA graphs is an NP-complete problem: In [Aho et al. 1977], it is shown that code generation for expressions with common subexpressions is NP-complete. Each instance of such a code generation problem is also a BURS code generation problem for SSA graphs. Thus it follows directly that BURS code generation for SSA graphs is NP-complete. 5.2 A Generic Checker for Code GeneratorsThe CGGG architecture can easily be extended for the program checking approach. Therefore we record which sequence of rewrite rules has been selected during the A*-search for the cheapest solution. This sequence of rewrite rules is the certificate. The checker takes it and recomputes the result. Page 206 This result is compared with the result of the code generator. Only if it is equal to that of the checker, the checker will output `yes'. If the checker outputs `no', then it has not been able to recompute the same result. Such a checker is generic in the sense that the respective BURS system is one of the checker inputs. Hence, the same generic checker can be used for all code generators generated by the CGGG system. It is particularly easy to extend the CGGG architecture such that it outputs the certificate necessary to check the results of the generated code generators. We can extend the BURS specification such that not only the machine code is output but also, in a separate file, the applied rules. Therefore, we only need to extend the EMIT part of each rule. This part contains instructions which will be executed on application of the rule. We can place one more instruction there, namely a protocol function. This protocol function writes a tuple to the certificate file. This tuple contains the applied rule as well as the node identifier of the node where it has been applied. We have decided to take the address in main memory of each node as its unique identifier. One might ask why it is not sufficient to check only the local decorations of the nodes on the solution path found during the A*-search to ensure the correctness of the computed result. The answer concerns the sorting of the nodes in the SSA graph. Each node has a specific sort which might be changed on application of a rule. Hence, the correctness of a rule sequence can only be decided if one makes sure that the sorts of the nodes and the sorts required by the rules fit together in each rule application. Moreover, one needs to check that the rules are applied according to the bottom-up strategy of BURS. We do not know of any other checking method assuring well-sorting and bottom-up rewriting other than recomputing the solution. The exact checking algorithm is summarized in figure 7. The certificate Certificate is a list of tuples, each containing a rule and the node identifier node_no. This node identifier characterizes uniquely the node at which the rule has been applied. BURS is the extended rewrite system which the CGGG has taken as input. SSA_Graph is the intermediate representation or the intermediate results obtained during the rewrite process, resp. Finally, Target_Code is the result of the rewrite process, the machine instruction sequence. To keep the presentation of the checking algorithm as simple as possible, we did not give all details of the auxiliary procedures but only described them colloquially. Clearly, this checker is generic because the respective BURS system is not hardwired into its code but one of the input parameters. Theorem 1 Correctness of Checker. If the checker outputs `yes'
(TRUE) on input (BURS, SSA_Graph, Target_Code, Certificate),
then the target code Target_Code has been produced correctly by
transforming the intermediate representation SSA_Graph according
to the rules of the BURS system BURS. Page 207 Proof. The CGGG system is supposed to generate code generators
implementing the respective input rewrite system BURS. To check
whether a code sequence produced by such a code generator is correct, we
need to make sure that there is a sequence of rule applications conforming
to the BURS rewrite method. Instead of testing if there is any such sequence
of rule applications, we check the weaker proposition if the certificate
produced by the code generator is a BURS rewrite sequence. This is done
successively by repeating each rule application, starting with the same
SSA intermediate representation. In each step, it is tested that the node
exists at which the rewrite step is supposed to take place. Then it is
tested that the rewrite step conforms to the bottom-up strategy of BURS.
Finally, the left-hand side of the rule must match the graph located at
the respective node. If all three requirements are fulfilled, then the
rewrite step is performed by the checker. If this recomputation of the
target machine code results in exactly the same code sequence, then the
result of the code generator has been tested. If we verify the checker
with respect to the requirements listed in this proof, then we have a formally
verified correct result of the code generation phase. 6 Backend Case Study and Experimental ResultsThe computations performed in the checker for the CGGG do the same rewrite steps as the backend itself and return `False' if an error occurs. The only difference between checker and backend lies in the search for the optimal solution. The checker gets it as input for granted while the backend needs to compute it by an extensive search. In subsection 6.1, we explain why this observation is a general property of NP-complete problem checkers. In subsection 6.2, we point out how we have exploited it in our checker implementation and state our experimental results. Finally, in subsection 6.3, we discuss and summarize the differences between black-box program checkers and program checkers using certificates from a practical point of view. 6.1 The Characteristic Trait of NPComplete Problem CheckersIt is a characteristic property of checkers for NP-complete problems that their implementation is part of the implementation for the NP-complete problem itself whose results they check. Program checkers for NP-complete problems have three inputs, the input and output of the implementation to be checked as well as a certificate describing how the implementation has computed the solution, cf. subsection 3.2. Based on the certificate, the checker recomputes the solution, compares it with the output of the implementation, and classifies the output as correct if and only if it is identical with its recomputed solution. Speaking in the language of Turing machines, the problem implementation is a nondeterministic Turing machine that needs good random guesses to find a solution. Page 208 The checker is a deterministic Turing machine that knows the good guesses (the certificate as its input) and just needs to recompute the solution. Hence, we can expect that the checker implementation is a part of the overall implementation of the optimization problem. Our case study confirmed this expectation. 6.2 Experimental ResultsFor BURS code generation, this expectation has come true. We could extract most of the code for the checker implementation from the code generator implementation directly. This is an advantage since CGGG has been tested extensively, making sure that many obvious bugs have been eliminated from the (implementation and checker) code already in the forefront of our experiment. CGGG has been used during the last four years by many graduate students who tend to be very critical software testers. Moreover, the CGGG system has been utilized to generate a compiler in the AJACS project (Applying Java to Automotive Control Systems) with industrial partners [Gaul 2002, Gaul et al. 2001]. This compiler transforms restricted Java programs into low-level C code. We found that we can distinguish between three different kinds of code in the CGGG implementation:
In our case study, we implemented a checker for the AJACS compiler described above. The table in figure 8 compares the overall size of the AJACS code generator generated by the CGGG system with the size of its checker. Both implementations, CGGG and the code generator, are written in C. If one wants to obtain formally verified solutions for the code generation phase, one needs to verify only the checker code. A first comparison between the size of the code generator and its checker shows that the verification effort for the checker seems to be half of that of the code generator. This comparison is only half the truth as the verification effort is even smaller. Much of the checker code is generated from the code generator specification. This is very simple code which just applies the rewrite rules. The verification conditions for the various rewrite rules are basically the same, simplifying the verification task considerably. Page 209 proc CGGG_Checker (BURS,
SSA_Graph, Target_Code, Certificate)
: Bool; proc apply_and_check (rule,
SSA_Graph, node_no) : Bool; proc find_node(SSA_Graph, node_no)
: proc BURS_successors(SSA_Graph, node_no)
: proc lhs(rule) : returns lefthand side of the rewrite rule rule; end proc match(pattern, node, SSA_Graph) : proc apply(rule, SSA_Graph, node_no) : does the rewrite step; end proc compare(Checker_Code, Target_Code)
: proc code(rule) : returns code associated with rule rule; end Figure 7: Checker for Code Generation
Figure 8: Size of Code Generator and Checker Page 210 In contrast, the code for the A*-search is very complicated and would need much more verification effort. Luckily it does not belong to the checker. Up to now we have not formally verified the checker code. For this task it seems helpful to parameterize the rewrite routines with the respective rewrite rules. In doing so, it would suffice to only formally verify the parameterized rewrite routine. We did not find any bugs in the AJACS compiler after having integrated our checker into it. 6.3 Black-Box Checking versus Checking with CertificatesIn the setting of black-box program checking, the checker and the program computing the solution are supposed to implement inherently different algorithms. Consequently, bugs in the program and bugs in its checker can be assumed to be independent. Hence, bugs in the program should be caught more likely when additionally using the checker. Program checking with certificates follows a completely different strategy. Instead of verifying the search for a solution together with the actual computation of this solution, we only verify its computation. Therefore, we partition the implementation computing an optimal solution into a correctness-critical part, into an optimality-critical part, and into a documentation part. To ensure correctness, we implement a checker by directly using the correctness-critical part. In this sense, program checking with certificates helps us in filtering those implementation parts which are correctness-critical and need to be verified in order to guarantee the formal correctness of the computed results. 7 Program Checking for Compiler FrontendsFrontend checking has been investigated in [Heberle et al. 1999]. In this section, we summarize these results in order to be able to classify them in section 8 according to our integrated view on all compiler passes. The semantics of programming languages is defined only with respect to the abstract syntax trees of programs, not with respect to the character sequences of input programs. We defined a compiler pass to be correct if it preserves the semantics, i.e. the observable behavior, of the translated programs. Hence, we cannot prove that a frontend transformation is semantics-preserving because a stream of characters or tokens does not have a formal semantics. This means that we need to refine our notion of correctness for the frontend computations as they are the compiler passes that compute the basis for all semantic definitions. Page 211 7.1 Checking Lexical AnalysisThe lexical analysis combines subsequent input characters into tokens, thereby eliminating meaningless characters such as whitespaces, line breaks, or comments. Identifiers (e.g. variable names) need special treatment. They are always mapped to one specific token, e.g. `IDENT'. The particular name of the identifier itself is stored in a separate table called symbol table. A similar approach is taken for numbers whose token is also unique, e.g. `REAL' or `INT', and whose value is stored in the symbol table as well. The lexical analysis is specified by finite automata together with the rule of the longest pattern (prefer the longest possible character sequence as possible) and priorities to avoid indeterminism. E.g. the sequence `w' `h' `i' `l' `e' is mapped to the token `WHILE', not to an identifier. All in all, the lexical analysis produces a unique result. The checker for the scanner needs to make sure that the computed token sequence has been computed according to the transition rules of the automaton. Therefore, the checker tries to recompute the character sequence of the input program given the token sequence of the scanner. It is fairly easy to recompute the character sequence of a single token. In case of an identifier, the corresponding identifier needs to be looked up in the symbol table. In case of a number token, the corresponding number is also looked up. Typically the representation of the number in the symbol table is different than the representation in the original program. Therefore one needs to prove that both representations, the one in the symbol table and the one in the original program, denote the same number. This check requires some case distinctions and can be done easily. The tokens for the predefined identifiers, operator symbols, etc. can be stored in a finite table together with their respective character sequence. Additional checking tasks are necessary to deal with the problem of whites-paces. There are pairs of subsequent tokens whose respective character sequences must be separated by whitespaces in the original program. For example, the character sequences for the tokens `WHILE' and `IDENT' need to be separated. If they were not separated, then the rule of the longest pattern would be applied, recognizing only one identifier consisting of the concatenation of the character sequence of the `WHILE' token and of the `IDENT' token. There are only finitely many different tokens. Hence, the pairs of tokens whose character sequences need to be separated by whitespaces can be enumerated in a table called conflict table. The checker for the lexical analysis has three inputs, the source program, the computed token sequence, and the symbol table. Based on the token sequence and the symbol table, it recomputes the character sequence. Thereby it inserts whitespaces if required by the conflict table. Then the checker compares the computed character sequence with the source program. Additional whitespaces between characters belonging to different tokens are always acceptable. Page 212 7.2 Checking Syntactic AnalysisThe syntactic analysis computes the context-free properties of programs which are expressed by deterministic context-free grammars. Given the token sequence of the lexical analysis, it computes the syntax tree of a program by using proqductions of the context-free grammar. Its result is unique. The checker for the parser needs to test if this syntax tree is a valid derivation. Furthermore, it needs to check whether the token sequence is the result of this derivation. This test can be done with the following top-down left-to-right recursive process along the syntax tree: Root Node: The root of the syntax tree must be annotated with the start symbol of the contextfree grammar. Inner Nodes: If an inner node of the syntax tree is annotated with a symbol X 0 and if it has n children nodes annotated with X1, . . . , Xn, then there must exist a production X0 -> X1 · · · Xn in the contextfree grammar. Leaves: Each leaf in the syntax tree must be annotated with a terminal symbol. If the concrete syntax tree has been simplified by transforming it into an abstract syntax tree, cf. section 4.1, then this simplification needs also to be checked. If this transformation from the concrete to the abstract syntax tree involves only local transformations of the syntax tree, then the corresponding check can be done easily. It is an open question of how to check the abstract syntax if also global transformations are applied. 7.3 Checking Semantic AnalysisThe semantic analysis computes contextsensitive properties of programs. These properties are expressed by attributes which are associated with the nodes in the abstract syntax tree of the program. Attributes are described by local attribution rules. These rules belong to particular productions of the underlying context-free grammar. Attribution rules may have conditions which must be fulfilled by a valid attribution. The checker for the semantic analysis takes the abstract syntax tree, the attributed abstract syntax tree, and the specification of the attribution rules as input. It checks if the attributed abstract syntax tree is a correct result of the semantic analysis. Therefore it must test whether the original abstract syntax tree and its attributed version are the same if one ignores the attribution. Furthermore, the checker must make sure that the attribution is consistent, i.e., that all attribution rules applied in the abstract syntax tree, in particular their conditions, are fulfilled. These are only local checks that can be done easily by traversing the abstract syntax tree in an arbitrary order: Page 213 Abstract Syntax Trees: The abstract syntax tree and its attributed version must be the same if one ignores the attribution. Attribution Rules: If an attribution rule r is associated with a production X0 -> X1 · · · Xn and if r has been used in to compute the attribution of a node X and its successors, then X must be annotated with X0 and it must have n successor nodes annotated with X1, . . . , Xn. Attribute Values: The values of the attributes of a node and its successor nodes must fulfill the applied local attribution rules. Conditions of Attribution Rules: The conditions of the applied local attribution rules must be fulfilled. The specification of the attribute grammar itself might not be trivial. E.g. for an incremental or a JIT compiler, one needs to specify type inference attribution rules which must adhere to the programming language semantics. The question whether such an attribute grammar is conform with the programming language specification might not be easy to answer. Also the computation of the attributes might involve complex traversals of the abstract syntax tree. Nevertheless, once the attribute grammar is established and the attributes are computed, the corresponding check whether the attributes are conform with the attribute grammar can be done locally and easily. 8 Evaluation of Frontend and Backend CheckersFrontend computations are inherently different compared to backend computations. This difference also determines the applicable checking methods. Front-ends compute uniquely determined results which can be checked by black-box program checking. Backend computations solve optimization problems whose solutions can be checked by program checking with certificates. In this section we establish an integrated view on the use of program checking in compilers by comparing frontend and backend checkers with respect to two criteria: Firstly we ask if it pays off to use program checking in order to establish formal correctness. Secondly we discuss if checkers can be generated in the same sense as compiler passes can be generated. 8.1 Evaluation of Frontend CheckersFormal Correctness and Verification The lexical and syntactic
analysis can be computed in linear time Page 214 Especially in the lexical analysis, the size of the checker is not smaller than the size of the corresponding scanner. If one wants to formally verify the lexical analysis, one has the choice of verifying the program code either of the checker or of the scanner directly. The latter seems to be simpler. For the syntactic analysis, this observation does not hold. The implementation of the syntactic analysis implements a pushdown automaton which is, in a practical sense, harder to verify than the simple checking procedure. Finally, the semantic analysis can be computed in polynomial time for nearly all programming languages of practical interest. The corresponding checker runs in linear time and performs much simpler computations. Hence, this checker is easier to verify. Concludingly, we see that if one wants to obtain formally correct results, the checker-based approach helps for the syntactic and for the semantic analysis. In these two cases, the corresponding checkers are much simpler and, in turn, easier to verify. For the lexical analysis, this does not hold. Checker and scanner seem to be equally diffcult to verify. Nevertheless, they do independent computations. This increases the probability of finding bugs in the checker-based approach, even without formal verification, since errors in the scanner and errors in its checker will hopefully not interact with each other. But this is no formal notion of correctness, only an increase in the trustworthiness of the scanner. Generating Frontend Checkers Today's compilers are generated and not written by hand. To establish the checker method as a practical way of constructing correct compilers, it is essential that checkers can be generated as well. This is indeed possible. For the syntactic and semantic analysis, this is fairly simple. A generic checker (the checker generator) can be parameterized with the context-free grammar and with the attribution rules, resp. Hence, the checker can be generated from the same specifications as the corresponding compiler pass. The checkers for the lexical analysis need as additional input the conflict table (and the symbol table which is part of the scanner's output). The conflict table can be generated automatically given the finite automaton specification for the scanner. These considerations show that each frontend compiler pass can be extended with a checker that can be generated from the same specification as the corresponding compiler pass itself. 8.2 Evaluation of Backend CheckersFormal Correctness and Verification Many backend problems are optimization problems. For them, program checking with certificates is the method of choice. This way of program checking helps to partition the implementation into two major parts, the optimality-critical part performing the search and the correctness-critical part computing the actual result. In our case study, we considered code generation based on rewrite systems. For this problem, we could separate the search part and the computation part. Page 215 The computation part becomes the principal part of the checker and needs to be formally verified. The search part determines how to compute the best solution and does not need to be verified. We are convinced that the implementations for most backend problems can be partitioned in the same way. Generating Backend Checkers It is essential that a checking method can be integrated into the generator methods well-known in compiler construction. This is the case for checkers for backends based on rewrite systems. Therefore, we simply need to parameterize the checkers with the rewrite rules of the code generator specification. 9 Related WorkCorrectness of compilers has been investigated in many approaches. The earliest such research [McCarthy and Painter 1967] focused on arithmetic expressions. Many approaches considered compilers based on denotational semantics, e.g. [Paulson 1981, Mosses 1992, Palsberg 1992], based on refinement calculi, e.g. [Müller-Olm 1997, Börger and Rosenzweig 1994, Börger and Durdanovic 1996], based on structural operational semantics, e.g. [Diehl 1996], or based on abstract state machines, e.g. [Börger and Rosenzweig 1994, Schellhorn and Ahrendt 1997, Börger and Durdanovic 1996, Stärk et al. 2001]. Most of these approaches did not consider compilation into machine code. Instead, they designed abstract machines and compiled input programs for interpreters of these abstract machines. Moreover, these approaches lead to monolithic architectures which did not allow to use the standard well-understood compiler architecture with its compiler generation tools nor did they allow for the reorganization of code on the machine code level. E.g. expressions are usually refined into postfix form and then interpreted on a stack machine. The efficiency of the generated code is by magnitudes worse than that of other compilers and, thus, does not meet practical requirements, cf. [Diehl 1996, Palsberg 1992]. The German Verifix project [Goerigk et al. 1996] has the goal of developing novel methods for the construction of correct compilers. This project has achieved progress by establishing the claim that it is possible to build provably correct compilers within the standard framework of compiler construction, especially by deploying compiler generators. Its results have been summarized in section 2. In the Verifix project, program checking has been proposed to ensure the correctness of compiler implementations. It has been successfully applied in the context of frontend verification, cf. section 7. It also claims to have dealt successfully with backend checking [Gaul et al. 1999, Gaul et al. 2000]. In particular, it claims to have built a checker for the BEG tool [Emmelmann 1992] which is based on pattern matching. Page 216 Nevertheless, these publications do not present a checking algorithm. They just claim that it is sufficient to check the annotations generated by a BEG code generator. It remains unclear how these annotations can be checked. We already argued in subsection 5.2 that, in contrast to their claims, it is necessary to recompute the solution because of three main reasons. Firstly, otherwise one could not make sure that the solution is computed according to a valid bottom-up rewrite strategy, i.e. that the order of the schedule in which the rules are applied is valid. Secondly, otherwise it could happen that some nodes with annotations are rewritten and eliminated without executing their annotated rewrite steps beforehand. In such cases, only incomplete code sequences would be the result. Thirdly, some rules are sorted. These sorts can be changed during the rewrite process. Therefore it is necessary to make sure that each rule is applied according to its sorts. We do not know of any other strategy than recomputing the solution that fulfills all three requirements. Certainly the results in [Gaul et al. 1999, Gaul et al. 2000] do not ensure these correctness requirements. The program checking approach has also been used in further projects aiming to implement correct compilers. In [Necula 2000], it is shown how some back-end optimizations of the GCC can be checked. Proof-carrying code is another weaker approach to the construction of correct compilers [Necula and Lee 1996, Necula and Lee 1997, Necula and Lee 1998, Colby et al. 2000] which guarantees that the generated code fulfills certain necessary correctness conditions. During the translation, a correctness proof for these conditions is constructed and delivered together with the generated code. A user may reconstruct the correctness proof by using a simple proof checking method. In recent work, a variant of proof-carrying code [Necula and Rahul 2001] has been proposed which is related to our notion of program checking with certificates. In this setting, trusted inference rules are represented as a higher-order logic program, the proof checker is replaced by a nondeterministic higher-order logic interpreter and the proof by an oracle implemented as a stream of bits that resolve the nondeterministic choices. This proof directly corresponds to our notion of certificate as it helps in resolving the nondeterminism in the same way as in our setting. Nevertheless, this work does not draw the same conclusion as we do, namely that checking with certificates isolates the correctness-critical part of an implementation. Pnueli [Pnueli et al. 1998b, Pnueli et al. 1998a] also addresses the problem of constructing correct compilers, but only for very limited applications. Only those programs consisting of a single loop with loop-free body are considered and translated without the usual optimizations of compiler construction, only refining translations are considered. Thereby, such programs are translated correctly such that certain safety and liveness properties of reactive systems are sustained. Page 217 In more recent work [Zuck et al. 2001], a theory for validating optimizing compilers is proposed which is similar to the method developed in the Verifix project. The main difference to our work is that these approaches do not assume to have access to the implementation of the compiler or its generator. This access gives us the freedom to modify the implementation to get a certificate used in the checker. As discussed in detail in section 3, the notion of program checking itself has been introduced in [Blum and Kannan 1995]. Our experiments show that for optimization problems, program checking with certificates helps in classifying the code of an implementation into the part which manages the search for an optimal solution and the part which makes sure that the computed solution is correct. To formally verify the correctness of the solutions computed by the implementation, it is sufficient to verify only this second part of it. Thus, program checking with certificates divides the implementation into two distinct parts, the search part and the correctness part. This is in contrast to the classical notion of black-box program checking which relies on the idea that errors in the implementation and in the checker are unlikely to depend on each other if implementation and checker compute different algorithms. 10 ConclusionsIn this paper, we have established an integrated view on all compiler passes and shown that the correctness of compiler implementations can be ensured by program checking. In particular, we have solved the open problem how program checking in optimzing compiler backends can be achieved. Therefore we have introduced the notion of program checking with certificates which can be applied for checking the correctness of solutions of NP-complete and optimization problems. Such problems might typically have several solutions of different quality. To prove their correctness, we do not need to consider their quality, a property which we exploit when checking programs with certificates. Backend computations are optimization problems. Most of their computation time and large parts of their code deal with the search for a good solution. We have extended these optimization algorithms such that they keep track of their search and output a certificate that tells us how the solution has been computed. This certificate is an additional input for the checker. The checker recomputes the solution with the help of the certificate, thereby avoiding any search. Furthermore, we have compared frontend and backend computations and identified a significant difference between them. In contrast to backend computations, frontend computations are characterized by the uniqueness of their solutions. This makes it possible that the checking algorithm follows a very different algorithm than the corresponding frontend algorithm implemented in the compiler. For the syntactic and the semantic analysis, we can save verification effort with the checking approach. Page 218 For the lexical analysis, the checking method does not reduce the verification amount. Concerning backend checking, program checking with certificates substantqially reduces the verification cost. All checkers can be generated from the same specifications as the corresponding compiler passes. We have tested our backend checking approach by designing and implementing a checker for a code generator used in an industrial project. This experiment proves that program checking with certificates can handle full real-life programming languages. This industrial code generator generates low-level C code. The same checking approach can be used without any modifications to ensure the correctness of native machine code generators. Since we have not modified the code generation algorithm itself (besides the protocol function), the efficiency of the generated code is not modified either. Our experiment has revealed that in this checker scenario with certificates, the checker can be extracted from the implementation, i.e., the checker code is part of the code of the implementation whose results are to be checked. This implies that program checking with certificates is also a method to isolate the correctness-critical parts of an implementation. In future work, we still need to show that the remaining, not yet considered backend tasks like e.g. register allocation or instruction scheduling can be handled with the same checking methods. Because their nature is similar to that of code generation (all of them are optimization problems), we are confident that program checking with certificates will be applicable for them as well. To prove this is subject of future work. Further open problems are the questions of how checking can be applied in incremental or JIT compilers and how the transformation into an intermediate representation as e.g. SSA form can be checked. Acknowledgements The author would like to thank Gerhard Goos and Wolf Zimmermann for many valuable discussions. Moreover, thanks to Jan Olaf Blech who implemented the checker for the AJACS compiler. Also thanks to Boris Boesler, Florian Liekweg, and Götz Lindenmaier for helpful discussions on the design of the checker for the AJACS compiler. Finally thanks to the anonymous reviewers for many helpful comments. References[Aho et al. 1977] Aho, A. V., Johnson, S. C., and Ullman, J. D. (1977). Code Generation for Expressions with Common Subexpressions. Journal of the Association for Computing Machinery, 24(1):146-160. [Blum and Kannan 1995] Blum, M. and Kannan, S. (1995). Designing Programs that Check Their Work. Journal of the ACM, 42(1):269-291. Preliminary version: Proceedings of the 21st ACM Symposium on Theory of Computing (1989), pp. 86-97. [Blum et al. 1993] Blum, M., Luby, M., and Rubinfeld, R. (1993). Self-Testing/Correcting with Applications to Numerical Problems. Journal of Computer and System Sciences, 47(3):549-595. Preliminary version: Proceedings 22nd ACM Symposium on Theory of Computing (1990), pp. 730-83. Page 219 [Boesler 1998] Boesler, B. (1998). Codeerzeugung aus Abhängigkeitsgraphen. Diplomarbeit, Universität Karlsruhe. [Börger and Durdanovic 1996] Börger, E. and Durdanovic, I. (1996). Correctness of compiling Occam to Transputer Code. Computer Journal, 39(1):52-92. [Börger and Rosenzweig 1994] Börger, E. and Rosenzweig, D. (1994). The WAM - definition and compiler correctness. In Beierle, L. and Pluemer, L., editors, Logic Programming: Formal Methods and Practical Applications. North-Holland Series in Computer Science and Artificial Intelligence. [Borland/Inprise 2002a] Borland/Inprise (2002a). Official Borland/Inprise Delphi-3 Compiler Bug List. http://www.borland.com/devsupport/delphi/fixes/3update/compiler.html. [Borland/Inprise 2002b] Borland/Inprise (2002b). Official Borland/Inprise Delphi-5 Compiler Bug List. http://www.borland.com/devsupport/delphi/fixes/delphi5/compiler.html. [Chirica and Martin 1986] Chirica, L. M. and Martin, D. F. (1986). Toward Compiler Implementation Correctness Proofs. ACM Transactions on Programming Languages and Systems, 8(2):185-214. [Colby et al. 2000] Colby, C., Lee, P., Necula, G. C., Blau, F., Plesko, M., and Cline, K. (2000). A Certifying Compiler for Java. In Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI'00), pages 95-107, Vancouver, British Columbia, Canada. [Cytron and Ferrante 1995] Cytron, R. and Ferrante,
J. (1995). Efficiently Computing [Cytron et al. 1989] Cytron, R., Ferrante, J., Rosen, B. K., Wegman, M. N., and Zadeck, F. K. (1989). An efficient Method of Computing Static Single Assignment Form. In Proceedings of the 16th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL'89), pages 25-35, Austin, Texas, USA. ACM Press. [Cytron et al. 1991] Cytron, R., Ferrante, J., Rosen, B. K., Wegman, M. N., and Zadeck, F. K. (1991). efficiently Computing Static Single Assignment Form and the Control Dependence Graph. ACM Transactions on Programming Languages and Systems, 13(4):451-490. [Dechter and Pearl 1985] Dechter, R. and Pearl, J. (1985). Generalized Best-First Search Strategies and the Optimality of A. Journal of the Association for Computing Machinery, 32(3):505-536. [Diehl 1996] Diehl, S. (1996). Semantics-Directed Generation of Compilers and Abstract Machines. PhD thesis, Universität Saarbrücken, Germany. [Dold et al. 1998] Dold, A., Gaul, T., and Zimmermann, W. (1998). Mechanized Verification of Compiler Backends. In Steffen, B. and Margaria, T., editors, Proceedings of the International Workshop on Software Tools for Technology Transfer (STTT'98), pages 13-24. [Dold and Vialard 2001] Dold, A. and Vialard, V. (2001). A Mechanically Verified Compiling Specification for a Lisp Compiler. In Proceedings of the 21st Conference on Software Technology and Theoretical Computer Science (FSTTCS 2001), pages 144-155, Bangalore, India. Springer Verlag, Lecture Notes in Computer Science, Vol. 2245. [Dold et al. 2002] Dold, A., von Henke, F. W., Vialard, V., and Goerigk, W. (2002). A Mechanically Verified Compiling Specification for a Realistic Compiler. Ulmer Informatik-Berichte 02-q03, Universität Ulm, Fakultät für Informatik. [Eli 2003] Eli (2003). Translator Construction Made Easy. http://www.cs.colorado.edu/~eliuser/. Page 220 [Emmelmann 1992] Emmelmann, H. (1992). Code selection by regularly controlled term rewriting. In Giegerich, R. and Graham, S., editors, Code Generation - Concepts, Tools, Techniques, Workshops in Computing. Springer Verlag. [Emmelmann 1994] Emmelmann, H. (1994). Codeselektion mit regul~ar gesteuerter Termersetzung. PhD thesis, Universit~at Karlsruhe, Fakultät für Informatik. [Emmelmann et al. 1989] Emmelmann, H., Schröer, F.-W., and Landwehr, R. (1989). BEG - A Generator for efficient Back Ends. In ACM Proceedings of the SIGPLAN Conference on Programming Languages Design and Implementation (PLDI'89), Portland, Oregon, USA. [Gaul 2002] Gaul, T. (2002). AJACS: Applying Java to Automotive Control Systems. Automotive Engineering Partners, 4. [Gaul et al. 1999] Gaul, T., Heberle, A., Zimmermann, W., and Goerigk, W. (1999). Construction of Verified Software Systems with Program-Checking: An Application to Compiler Back-Ends. In Proceedings of the Workshop on Runtime Result Verification (RTRV'99). [Gaul et al. 2001] Gaul, T., Kung, A., and Charousset, J. (2001). AJACS: Applying Java to Automotive Control Systems. In Grote, C. and Ester, R., editors, Conferqence Proceedings of Embedded Intelligence 2001, Nürnberg, pages 425-434. Design & Elektronik. [Gaul et al. 2000] Gaul, T., Zimmermann, W., and Goerigk, W. (2000). Practical Construction of Correct Compiler Implementations by Runtime Result Verification. In Proc. SCI'2000, International Conference on Information Systems Analysis and Synthesis, Orlando, Florida, USA. [Goerigk et al. 1996] Goerigk, W., Dold, A., Gaul, T., Goos, G., Heberle, A., von Henke, F., Hoffmann, U., Langmaack, H., Pfeifer, H., Ruess, H., and Zimmermann, W. (1996). Compiler Correctness and Implementation Verification: The Verifix Approach. In Fritzson, P., editor, Poster Session of CC'96. IDA Technical Report LiTH-IDA-R-96-12, Linkoeping, Sweden. [Goerigk et al. 1998] Goerigk, W., Gaul, T., and Zimmermann, W. (1998). Correct Programs without Proof? On Checker-Based Program Verification. In Tool Support for System Specification and Verification, ATOOLS'98, pages 108-123, Malente, Germany. Springer Series Advances in Computing Science. [Goos and Zimmermann 1999] Goos, G. and Zimmermann, W. (1999). Verification of Compilers. In Olderog, E.-R. and Steffen, B., editors, Correct System Design, pages 201-230. Springer-Verlag, Lecture Notes in Computer Science, Vol. 1710. [Goos and Zimmermann 2000] Goos, G. and Zimmermann, W. (2000). Verifying Compilers and ASMs or ASMs for uniform description of multistep transformations. In Gurevich, Y., Kutter, P. W., Odersky, M., and Thiele, L., editors, Proceedings of the International Workshop ASM 2000, Abstract State Machines - Theory and Applications, pages 177-202, Monte Verit, Switzerland. Springer-Verlag, Lecture Notes in Computer Science, Vol. 1912. [Heberle et al. 1999] Heberle, A., Gaul, T., Goerigk, W., Goos, G., and Zimmermann, W. (1999). Construction of Verified Compiler Front-Ends with Program-Checking. In Bjørner, D., Broy, M., and Zamulin, A., editors, Perspectives of System Informatics, Third International Andrei Ershov Memorial Conference, PSI'99, pages 493-502, Akademgorodok, Novosibirsk, Russia. Springer Lecture Notes in Computer Science, Vol. 1755. [Martin 1998] Martin, F. (1998). PAG - an efficient program analyzer generator. International Journal on Software Tools for Technology Transfer, 2(1):46-67. [McCarthy and Painter 1967] McCarthy, J. and Painter, J. (1967). Correctness of a Compiler for Arithmetic Expressions. In Schwartz, J. T., editor, Mathematical Aspects of Computer Science, Proceedings of Symposia in Applied Mathematics, pages 33-41. American Mathematical Society. [Mosses 1992] Mosses, P. D. (1992). Action Semantics. Cambridge University Press. Page 221 [Müller-Olm 1997] Müller-Olm, M. (1997). Modular Compiler Verification : A Refinement-Algebraic Approach Advocating Stepwise Abstraction. Springer Verlag, Lecture Notes in Computer Science, Vol. 1283. PhD dissertation, Technische Fakultät der Christian-Albrechts-Universität zu Kiel, Germany, 1996. [Necula 2000] Necula, G. C. (2000). Translation Validation for an Optimizing Compiler. In Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI'00), pages 83-94, Vancouver, British Columbia, Canada. [Necula and Lee 1996] Necula, G. C. and Lee, P. (1996). ProofCarrying Code. Technical Report CMU-CS-96-165, School of Computer Science, Carnegie Mellon University, Pittsburgh, PA 15213, USA. [Necula and Lee 1997] Necula, G. C. and Lee, P. (1997). Proof-Carrying Code. In Proceedings of the 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL'97), pages 106-119, Paris, France. [Necula and Lee 1998] Necula, G. C. and Lee, P. (1998). The Design and Implementation of a Certifying Compiler. In Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI'98), pages 333-344, Montreal, Quebec, Canada. [Necula and Rahul 2001] Necula, G. C. and Rahul, S. P. (2001). Oracle-Based Checking of Untrusted Software. In Proceedings of the 28th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL'01), pages 142-154, London, UK. [Newsticker 2001] Newsticker, H. (2001). Rotstich durch Fehler in Intels C++ Compiler. http://www.heise.de/newsticker/data/hes11.11.01000/. [Nymeyer and Katoen 1997] Nymeyer, A. and Katoen, J.-P. (1997). Code generation based on formal BURS theory and heuristic search. Acta Informatica 34, pages 597-635. [Palsberg 1992] Palsberg, J. (1992). Provably Correct Compiler Generation. PhD thesis, Department of Computer Science, University of Aarhus, Denmark. [Papadimitriou 1994] Papadimitriou, C. H. (1994). Computational Complexity. Addison-Wesley Publishing Company. [Paulson 1981] Paulson, L. (1981). A Compiler Generator for Semantic Grammars. PhD thesis, Department of Computer Science, Stanford University, Stanford, Cali fornia, USA. [Pnueli et al. 1998a] Pnueli, A., Shtrichman, O., and Siegel, M. (1998a). The code validation tool (cvt.). International Journal on Software Tools for Technology Transfer, 2(2):192-201. [Pnueli et al. 1998b] Pnueli, A., Siegel, M., and Singermann, E. (1998b). Translation validation. In Steffen, B., editor, Proceedings of Tools and Algorithms for the Construction and Analysis of Systems, pages 151-166, Lisbon, Portugal. Springer Verlag, Lecture Notes in Computer Science, Vol. 1384. [Polak 1981] Polak, W. (1981). Compiler Specification and Verification. Springer Verlag, Lecture Notes in Computer Science, Vol. 124. [Schellhorn and Ahrendt 1997] Schellhorn, G. and Ahrendt, W. (1997). Reasoning about Abstract State Machines: The WAM Case Study. Journal of Universal Computer Science, 3(4):377-413. [Stärk et al. 2001] Stärk, R., Schmid, J., and Börger, E. (2001). Java and the Java Virtual Machine: Definition, Verification, Validation. Springer Verlag. [Zimmermann and Gaul 1997] Zimmermann, W. and Gaul, T. (1997). On the Construction of Correct Compiler Backends: An ASM Approach. Journal of Universal Computer Science, 3(5):504-567. [Zuck et al. 2001] Zuck, L., Pnueli, A., and Leviathan, R. (2001). Validation of Optimizing Compilers. Technical Report MCS01-12, Faculty of Mathematics and Computer Science, The Weizmann Institute of Science. Page 222 |
||||||||||||||||||||||||||
 implementing f. Thereby
the checker should be simpler than the implementation of f itself
and, a stronger requirement, simpler than any implementation
implementing f. Thereby
the checker should be simpler than the implementation of f itself
and, a stronger requirement, simpler than any implementation 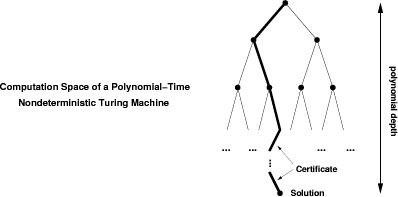
 L, there
exists y, |y|
L, there
exists y, |y|  poly(x) such that M
accepts (x, y). Hence, for any language L in NP, there
is a simple proof checker (the polynomial time Turing machine M)
and a short proof (y) for every string x # L. Given
the proof y and the string x, the proof checker M
can decide if the proof is valid. Clearly, the two definitions are equivalent:
Computations within nondeterministic polynomial time can be thought of
as a search tree with polynomial depth. Each node represents the choice
which the nondeterministic Turing machine has at any one time during computation.
A proof for membership in the language L is a path to a solution
during this search tree. Since the tree has polynomial depth, there always
exists a proof of polynomial length. Such a proof is also called a certificate,
cf. [
poly(x) such that M
accepts (x, y). Hence, for any language L in NP, there
is a simple proof checker (the polynomial time Turing machine M)
and a short proof (y) for every string x # L. Given
the proof y and the string x, the proof checker M
can decide if the proof is valid. Clearly, the two definitions are equivalent:
Computations within nondeterministic polynomial time can be thought of
as a search tree with polynomial depth. Each node represents the choice
which the nondeterministic Turing machine has at any one time during computation.
A proof for membership in the language L is a path to a solution
during this search tree. Since the tree has polynomial depth, there always
exists a proof of polynomial length. Such a proof is also called a certificate,
cf. [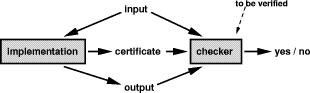
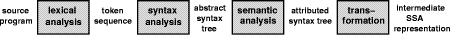
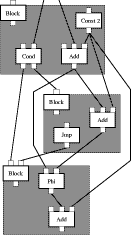
 nodes, x
=
nodes, x
= 
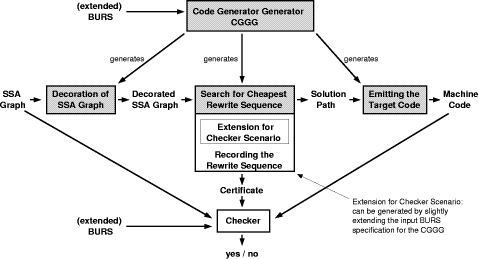


 [] do
[] do
 BURS
then return False;
BURS
then return False;  then
return False;
then
return False;  (n) where n is the size of the
input program. Their checkers need linear time as well. Hence, in the formal
sense described in
(n) where n is the size of the
input program. Their checkers need linear time as well. Hence, in the formal
sense described in