| Submission Procedure |
What Is the Value of Taxicab(6)?Cristian S. Calude Elena Calude Michael J. Dinneen Abstract: For almost 350 years it was known that 1729 is the smallest integer which can be expressed as the sum of two positive cubes in two different ways. Motivated by a famous story involving Hardy and Ramanujan, a class of numbers called Taxicab Numbers has been defined: Taxicab(k, j, n) is the smallest number which can be expressed as the sum of j kth powers in n different ways. So, Taxicab(3, 2, 2) = 1729; Taxicab(4, 2, 2) = 635318657. Computing Taxicab Numbers is challenging and interesting, both from mathematical and programming points of view. The exact value of Taxicab(6) = Taxicab(3, 2, 6) is not known; however, recent results announced by Rathbun [R2002] show that Taxicab(6) is in the interval [10 18 , 24153319581254312065344]. In this note we show that with probability greater than 99%, Taxicab(6) = 24153319581254312065344. Key Words: HardyRamanujan Number, Taxicab Number, sampling Category: G.3 1 Is 1729 a Dull Number?Srinivasa Ramanujan was one of India's greatest, largely self-taught, mathematical geniuses. In January 1913 Ramanujan, after seeing the book Orders of Infinity, wrote to its author, the distinguished number theorist G. H. Hardy. Hardy and Littlewod studied the long list of unproved theorems which Ramanujan enclosed with his letter and sent him the letter beginning with the famous paragraph: I was exceedingly interested by your letter and by the theorems which you state. You will however understand that, before I can judge properly of the value of what you have done, it is essential that I should see proofs of some of your assertions. Your results seem to me to fall into roughly three classes: Page 1198
In 1914 Ramanujan arrived in England and for a couple of years Hardy and Ramanjuan had a collaboration which led to important results. The following is a famous story told by Hardy, repeated word for word in various sources. Ramanjuan became ill in 1917 and at the age of 33 lay dying in Putney hospital. Hardy on a visit to his colleague, moved and at a loss for words, could only say "I came in a taxi 1729, that's a pretty dull number." Ramanujan's immediate rejoinder was "Oh no Hardy. 1729 is the smallest integer which can be expressed in two different ways as the sum of two cubes."1 This episode prompted Littlewood to say that "every positive integer was one of [Ramanujans'] personal friends". The number 1729 has since become known as the Hardy-Ramanujan Number, even though this feature of 1729 was known more than 300 years before Ramanujan (more precisely, by Bernard Frénicle de Bessy in 1657, cf. [BB1993]). Is 1729 really a dull number? Not at all. First, 1729 is a Carmichael Number, i.e., a pseudoprime relative to every base. Also note after [D] that, beginning at the 1729th decimal digit of the transcental number e, the next ten successive digits of e are 0719425863, in the first appearance of all ten digits in a row without repititions. Finally, are there any dull natural numbers? We can prove that there are none. Indeed, if there are dull numbers, then we can divide all numbers into two sets - interesting and dull. We then pick up the smallest dull number. Since it is the smallest uninteresting number it becomes, ipso facto, an interesting number. We must therefore remove it from the dull set and place it in the other set. But now there will be another smallest dull number. Repeating this process will make any dull number interesting. 2 How Many Taxicab Numbers Are Known?The smallest number expressible as the sum of two cubes in n different ways is called the Taxicab Number Taxicab(n), that is Taxicab(n) = Taxicab(3, 2, n). Hardy and Wright [HW1954] (Theorem 412) have proven that the Taxicab(n) exists for every positive integer n, but the proof is of little use in finding the number.
1More accurately, "1729 is the smallest integer which can be expressed as the sum of two positive cubes in two different ways." Page 1197 Trivially, Taxicab(1) = 2 = 13 + 13. The next number, Taxicab(2) = 1729 = 13 + 123 = 93 + 103, is the HardyRamanujan Number; see Butcher [B1998] for all solutions of the equation a3 + b3 = A3 +B3. In 1957, Leech [L1957] computed Taxicab(3) = 87539319 = 1673 + 4363 = 2283 + 4233 = 2553 + 4143, in 1991 Rosenstiel, Dardis, and Rosenstiel [RDR1991] (see also Butler's program [B2001]) showed that Taxicab(4)
= 6963472309248 = 24213 + 190833 and in 1997 Wilson [W1999] discovered the fifth Taxicab Number, Taxicab(5) = 48988659276962496
= 387873 + 3657573 In 1998 Bernstein (see [B2000]) discovered that 391909274215699968
is a six-way sum of cubes and showed that Taxicab(6) Taxicab(6) To appreciate the gap between 1018 and 24153319581254312065344 note that the last number is approximately 2.4 · 1022. In May 2003, Gascoigne [G2003] verified that Taxicab(6) > 6.8 · 1019. Page 1198 3 A Probabilistic Approach to the Computation of Taxicab(6)There are various approaches to the computation of Taxicab, see [S, P2002, S2003, T]. The main idea is to use an effcient codification and a "computational structure'' that supports insertion of new elements and removal of the smallest element (somethimes referred to as "priority queues''). For example, Bernstein [B2000] codes the pairs as a3 + 2b3 + 3c3 = 4d3 (1) and computes all positive integers a, b, c, d
None of these approaches may directly work for the calculation of Taxicab(6). So, in what follows we are going to use a sampling approach (see [C1977]; for an application to automata theory see [CCCDN2001]). The result will not be exact, but the error will be less than 1%. Here is the method. Given a finite population of size N, we will
estimate 3 proportions associated with 3 binary random variables, Pi
= P (Xi = 1), i = 1, 2, 3, using a
pseudorandom sample of size n. Each estimate should be correct
within ±c% in the sense that, if the sample shows pi
to be Pi, the percentage for the whole population is
"sure'' to lie between pi - c% and pi
+ c% (with "accuracy within c%"). As we cannot guarantee
an accuracy within c%, we accept a probability The process of random generation of the sample is equivalent with sampling
with replacement (generated units are independent, repetitions are possible),
according to a Binomial scheme. If (u1, . . . , un)
are generated items, we denote by mi the number of items
for which Xi (u) = 1, i = 1, 2, 3. Then,
the estimates of Pi are pi = In order to estimate the value of n, we start from the simultaneous conditions
where Accordingly, we will have
hence, the sample size is
Page 1199 The value of n depends on the unknown proportions Pi. As we don't have any knowledge regarding Pi, we will choose the "critical" value P = 50% (which maximizes the product P (1 - P )). Hence, the "safest" estimation of the sample size
The parameters 4 The ProgramOur program reads the sample random numbers (generated in a standard way with Mathematica) and tests them; it either finds a smaller six-qway sum of cubes (in which case it improves the current bound, but doesn't necessarily obtain the exact value of Taxicab(6)) or gives a strong plausibility argument against the possibility of finding a smaller six-way sum of cubes. The second alternatives happens in our case. The program (written for this present research, not as a package application), listed in Appendix, Figure 1, uses version 4.1.2 of GMP (GNU Multiple Precision) library, [GNU]. To save on computation time we first precompute all of the possible cubes up to the maximum input value. These are stored in the vector v(N) in increasing order so that we can decide if a number is a cube root in lg N time (see binary_search conditional). On input str we subtract each possible cube in v(N) from the integer representation currentSum and count how many of those differences are also cubes. Theoretically, in terms of N (the cube root of our input upper
bound) the program runs in time O(N · n ·
log N) for a single input number of size n bits. So, when
n = lg2 (N3), the largest
input size, we can replace N with Page 1200 However, note that this bound is more pessimistic than the worstcase scenario since not all iterations of our binary_search call are carried out. The memory size of the program is only dependant on the variable
N, not the number of cases (which depends on c and 5 Generalisations of Taxicab NumbersWe can define Taxicab Numbers for higher powers than three as well as for more representations. In general, Taxicab(k, j, n) is the smallest number which can be expressed as the sum of j kth powers in n different ways. For example, Taxicab(4, 2, 2) is the smallest number that is a sum of two fourth powers in two different ways. Euler has shown that Taxicab(4, 2, 2) = 635318657 = 594 + 1584 = 1334 + 1344, but no example is known for 3way sums or more; for fifth powers no example of a 2way sum is known, Schneider [S2003]. The following Taxicab Numbers can be easily computed: Taxicab(2, 3, 2) = 62 = 12 + 52 + 62
= 22 + 32 + 72, When generalizing to higher powers it is not known if nway sums for higher powers exist, cf. Schneider [S2003]. Other generalisations are obtained by allowing both positive and negative terms. For more information see [S, P2002, S2003, T]. Acknowledgement The authors wish to thank all four referees for their comments and suggestions. References[BB1993] B. C. Berndt, S. Bhargava. Ramanujan-for lowbrows, Am. Math. Monthly 100 (1993), 645--656. Page 1201 [B2000] D. J. Bernstein. Enumerating solutions to p(a) + q(b) = r(c) + s(d), Mathematics of Computation 70, 233 (2000), 389--394. [B1998] J. Butcher. Hardy's taxi, x2 +3y2 = p and Michael Lennon , NZMS Newsletter 76 (1999). http://www.math.auckland.ac.nz/~butcher/miniature/. [B2001] B. Butler. C Program for Ramanujan Quadruples, http://www.durangobill.com/Rama4.html, 30 May 2001. [CCCDN2001] C. S. Calude, Elena Calude, Terry Chiu, Monica Dumitrescu, R. Nicolescu. Testing computational complementarity for Mermin automata, J. Multi Valued Logic, 6 (2001), 47-65. [C1977] W. G. Cochran. Sampling Techniques, John Wiley, New York, 1977 (third edition). [G2003] S. Gascoigne, http://euler.free.fr/taxicab.htm, May 2003. [H1965] A. Hald. Statistical Tables and Formulas, John Wiley, New York, 1965. [HW1954] G. H. Hardy, E. M. Wright. An Introduction to the Theory of Numbers, Oxford University Press, London, 1954, 3rd edition. [L1957] J. Leech. Some solutions of Diophantine equations, Proc. Cambridge Phil. Soc. 53 (1957), 778-780. [P2002] I. Peterson. Taxicab Numbers, Science News Online, http://www.science news.org/20020727/mathtrek.asp. [R2002] R. L. Rathbun. Sixth Taxicab Number?, http://listserv.nodak.edu/ scripts/wa.exe?A2=ind0207&L=nmbrthry&P=R530, July 16, 2002. [RDR1991] E. Rosenstiel, J. A. Dardis, C. R. Rosenstiel. The four least solutions in distinct positive integers of the Diophantine equation s = x3 + y3 = z3 + w3 = u3 + v3 = m3 + n3 , Bull. Inst. Math. Appl. 27 (1991), 155-157. [S2003] W. Schneider. Taxicab Numbers, http://www.wschnei.de/numbertheory/ taxicabnumbers.html, 3 February 2003. [W1999] D. W. Wilson. The fifth Taxicab Number is 48 988 659 276 962 496, J. Integer Seq. 2 (1999), Article 99.1.9, 1, http://www.research.att.com/~njas/sequences /JIS/wilson10.html. [S] N. J. A. Sloane. Sequence A011541, OnLine Encyclopedia of Integer Sequences, http://www.research.att.com/cgibin/access.cgi/as/njas/sequences/eisA. cgi?Anum=A011541. [T] The Taxicab Problem, http://euler.free.fr/taxicab.htm. [D] The Dullness of 1729, http://www.mathpages.com/home/kmath028.htm. [GNU] The GNU GMP library, http://www.swox.com/gmp/. Page 1202 APPENDIX
/*
* Program to check for whether a set of integers can be expressed in NR
* different ways as a sum of two positive integer cubes. 20 May 2003
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <gmpxx.h>
using namespace std;
const unsigned long N = 28906206; // cube root of upper bound on input
const unsigned long NR = 6; // our target taxicab count
int main(){
mpz_class t1, t2;
vector<mpz_class> v(N);
for (unsigned long i=0; i<N; ++i)
{// create the vector of cubic values
t1 = i+1; t2 = t1*t1; v[i] = t2*t1;
}
string str; // input number as string
mpz_class currentSum; // input number as MP integer
mpz_class N_a3; // test cube
unsigned long a; // test cube root
while (true){
cin >> str; if (str.length()==1) break;
currentSum=str;
cout << "processing: " << currentSum << endl;
int cnt=0;
for (a=0; a<N-1; a++){
N_a3 = currentSumv[a];
if (N_a3 < v[a]) break;
if ( binary_search(v.begin(), v.end(), N_a3) ){
cnt++;
if (cnt > maxcnt) { maxcnt = cnt; cerr << "maxcnt=" <<
cnt <<endl; }
vector<mpz_class>::iterator VI = lower_bound(v.begin(),
v.end(), N_a3);
cout << "a=" << (a+1) << ' ' << "b=" << (VIv.begin())+1
<<endl;
}
if (cnt == NR){ cout << "Found taxicab(NR)!" << endl; return 1;}
}
}
return 0; // end of processing
}
Figure 1: A simple C++ program that tests for Taxicab numbers. Page 1203 |
|||||||||||||||||
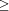 1018. In 2002 Rathbun [
1018. In 2002 Rathbun [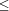 24153319581254312065344 = 289062063 + 5821623
24153319581254312065344 = 289062063 + 5821623  (0.0027 in our case) of getting "an unlucky sample" (which is
in error by more than the desired c%).
(0.0027 in our case) of getting "an unlucky sample" (which is
in error by more than the desired c%). 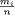 i = 1, 2, 3. For a large value of n (n > 100), one can
use the normal approximation for pi, that is, pi
is approximately normal distributed N
i = 1, 2, 3. For a large value of n (n > 100), one can
use the normal approximation for pi, that is, pi
is approximately normal distributed N 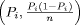 .
.
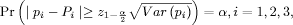
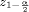 is the
(1 -
is the
(1 - 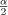 )-quantile
of the N (0, 1) distribution, and z 0.99865 #
3 (see, for instance, [
)-quantile
of the N (0, 1) distribution, and z 0.99865 #
3 (see, for instance, [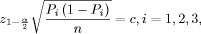
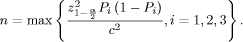
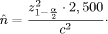
 -
= 3. For an accuracy within c = 5% we get
-
= 3. For an accuracy within c = 5% we get  = 900 (small, less significant) and for c = 6.041/2
= 900 (small, less significant) and for c = 6.041/2 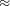 2.45%,
2.45%, 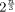 to see that we have an exponentialtime O(
to see that we have an exponentialtime O(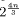 · n) algorithm.
· n) algorithm.