| Submission Procedure |
TOY LISP INTERPRETER ON A CONNEX MEMORY MACHINE *1
Abstract: The Connex Memory is a new memory structure proposed by G. Stefan as a hardware support for symbolic processing. The powerful set of memory access functions supported by the CM is expected to allow a faster and less resource consuming execution of functional languages on dedicated architectures. This paper presents an interpreter of Chaitin's Toy LISP written for a CM-based system with stack controller. *1 C. Calude (ed.). The Finite, the Unbounded and the Infinite, Proceedings of the Summer School "Chaitin Complexity and Applications", Mangalia, Romania, 27 June - 6 July, 1995. 1 Introduction
The Connex Memory is a new memory structure proposed in [2] and [3] as a hardware support for symbolic processing. Paying a price in increasing the complexity of the memory cell by a reasonable constant, the CM makes available a set of powerful memory access functions. The CM consists of a content addressable list implemented as a bidirectional shift register (the shift can begin at any specified point in the list). While a conventional CAM uses fix dimension large words in arbitrary order, the CM content is a string of symbols in a natural representation, consecutive symbols in the string being stored in consecutive cells. This particular feature of the CM supports a simple accommodation of variable length words since any string of symbols can be located in time proportional to the length of the string. Working with the CM is much like using a text editor: a cursor can be moved to the left, to the right, or placed after the first occurrence of a given string. At the cursor position a symbol can be inserted or deleted while preserving the continuity of the CM content. As a consequence, the search of a string in CM is a parallel one, rather then a sequential one. This paper presents a string reduction interpreter of Chaitin's Toy LISP [1] written for a CM-based system [4] with stack controller. The CM functions were emulated by the following PASCAL subroutines (*2): FIND(m,s) marks with marker m each symbol immediately following an occurrence of the string s; the leftmost symbol marked (the "output") is stored in OutCM[m]. *2 All the software can be obtained sending an e-mail to bogdan@hera.gef.pub.ro. Page 427 INSERT(m,s) inserts the symbol (string) s at the position of the leftmost marker m; the marker m is moved one place after the string inserted. DELETE(m) deletes the leftmost symbol marked with marker m ; the following symbol is marked and stored in OutCM[m]. RIGHT(m) moves the markers one place to the right; the leftmost symbol marked with marker m is stored in OutCM[m]. LEFT(m) moves the markers one place t o the left; the leftmost symbol marked with marker m is stored in OutCM[m]. NOOP(m) the leftmost symbol marked with marker m is stored in OutCM[m] (useful when the current marker is changed). SETPOINTER(m,k) the first symbol marked with m is also marked with k. ENDSEX(m) moves the marker m one s-expression to the right. BACKSEX(m) moves the marker m at the beginning of the current s-expression. CLRBR(m) deletes the parentheses enclosing the current s-expression. The last three functions do not belong to the original set of CM functions [2]. They were initially implemented as subroutines, but since they proved to be frequently called by the interpreter, solutions were found to implement them in the CM hardware and they were added to the CM set of functions as atomic operations. 2 The Interpreter
When the interpreter is started, the CM should contain both the s-expression to be evaluated and the context of evaluation, if any, as a string of symbols of the form: @environment$s-expression% where @ and $ are special symbols indicating the beginning of the environment and of the s-expression, respectively. During the evaluation process the length of the environment and of the s-expression varies. The evaluation terminates with the original s-expression replaced by its value and with the marker m placed at the beginning of the result (see figure 1). 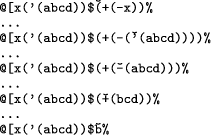
Page 428 The environment consists of pairs variable-value of the form [xv where [ is a special symbol, unique for each environment. The distinction between different environments that may coexist is necessary for the function EVAL which requires an evaluation in a new environment, initially void. In our interpreter these special symbols are graphical symbols starting with ASCII code 179. All the functions of the toy LISP presented in [1] were implemented with the exception of the function TRY. The interpreter was tested using some recursive functions, most of them from [1]. They are listed below together with their execution time (in CM cycles) and memory requirement (the maximum number of CM cells used at any one time).
- Name First atom of
((((a)b)c)d)@$(('(&(F)(F('((((a)b)c)d)))))('(&(x)(/(.(,x))x(F(+x)))))))% - Name Concatenation of (ab) and (cd) - Name Flatten (a(b)c) - Name Flatten (a(b(c)d)e) - Name Last of (a(b)c) - Name Reverse (abcd) Page 429
Name Unshuffle (abc)(123) 3 Conclusions
We have presented a toy LISP interpreter and some running examples on a LISP-oriented architecture. The heart of this architecture is a new memory structure called the Connex Memory which supports a natural representation and a simple manipulation of the list structures. Due to the powerful set of functions offered by the CM, the interpreter has a compact form - only 350 lines of PASCAL code. The few running examples presented here are certainly not enough for a proper evaluation of the interpreter performance, but they suggest that the interpreter is also fast and uses a small amount of CM cells. The use of this interpreter in Chaitin's construction of a diophantine equation corresponding to the number Omega might result in a significant simplification of this equation. Page 430 References
[1] G. Chaitin, Algorithmic Information Theory, Cambridge University Press, 1987. [2] G. Stefan, "The Connex Memory. A Physical Support for Tree/List Processing," Technical Report, Center for New Electronic Architecture of the Romanian Academy, Feb. 1994. [3] Z. Hascsi, G. Stefan, "The Connex Content Addressable Memory (C 2 AM)," Proc. 21-th ESSCIRC'95, Lille-France, Sep. 1995, pp. 422-425. [4] G. Stefan, Mihaela Malitza, "Chaitin ToyLisp on Connex Memory Machine," this volume. [5] P. H. Winston, B. K. P. Horn, LISP, Addison Wesley, 1981. A ToyLISP Interpreter
{Toy LISP Interpreter}
var R, gencar, env_top, bara, bara_def : char;
e, v : byte;
procedure COPY(s, d: integer); { (abc) --> (abc)...(abc) }
begin
SETPOINTER (p6, s);
ENDSEX (p6);
INSERT (p6, ']');
while OUTCM [s] <> ']' do begin
R:= OUTCM [s];
INSERT (d, R);
RIGHT (s);
end;
DELETE (s);
LEFT (d);
BACKSEX (d);
end;
procedure MOVE (s, d:integer); { .(abc)..... --> .....(abc). }
begin
SETPOINTER (p6, s);
ENDSEX (p6);
INSERT (p6, ']');
while OUTCM [s] <> ']' do begin
R:= OUTCM [s];
DELETE (s);
INSERT (d, R);
end;
DELETE (s);
end;
procedure CLRSEX (m: byte); { ...(abc)... --> ...... }
begin
SETPOINTER (p6, m);
ENDSEX (p6);
INSERT (p6, ']');
repeat
DELETE (m);
until OUTCM [m] = ']';
DELETE (m);
end;
procedure LISTA_VIDA; { ...()... --> ...()... }
begin
LEFT (m);
end;
Page 431
procedure EVAL; forward;
procedure ATOM; { ..x.. --> ..1.. }
begin { ..().. --> ..1.. }
DELETE (m); { ..(abc).. --> ..0.. }
EVAL;
if OutCM [m] <> '(' then begin
DELETE (m);
INSERT (m, '1'); end
else begin
RIGHT (m);
if OutCM [m] = ')' then begin
LEFT (m);
INSERT (m, '1'); end
else begin
LEFT (m);
INSERT (m, '0'); end;
CLRSEX (m); end;
BACKSEX (m);
CLRBR (m);
end;
procedure PUT_IN_ENV; { @$...xv --> @{-[xv$... }
begin
R := OutCM [m];
FIND (e, env_top);
INSERT (e, bara_def);
INSERT (e, bara);
INSERT (e, R);
RIGHT (m);
MOVE (m, e);
end;
procedure DEFINE; { (&xa) --> @[xa..$.. }
begin
DELETE (m);
if OutCM [m] <> '(' then begin
RIGHT (m);
EVAL;
LEFT (m);
PUT_IN_ENV;
BACKSEX (m);
CLRBR (m); end
else begin
RIGHT (m);
R := OutCM [m];
DELETE (m);
LEFT (m);
INSERT (m, '&');
Page 432
LEFT (m);
LEFT (m);
INSERT (m, R);
LEFT (m);
PUT_IN_ENV; end;
end;
procedure DO_PAIRS; { ...xy...ab... --> @[xa[yb... }
begin
FIND (e, env_top);
INSERT (e, env_top);
LEFT (e);
NOOP (m);
while OutCM [m] <> ')' do begin
R := OutCM [m];
INSERT (e, bara);
INSERT (e, R);
NOOP (p5);
MOVE (p5, e);
DELETE (m);
end;
end;
procedure REMOVE_PAIRS; { @[xa[yb...@$... --> @$... }
begin
FIND (e, env_top);
while OutCM [e] <> env_top do
if OutCM [e] = bara_def then begin
RIGHT (e);
RIGHT (e);
RIGHT (e);
ENDSEX (e); end
else DELETE (e);
DELETE (e);
end;
procedure LAMBDA; { ((&(xy)f)ab) --> @[xa[yb..$..f.. }
begin
LEFT (m);
ENDSEX (m);
while OutCM [m] <> ')' do begin
EVAL;
ENDSEX (m); end;
BACKSEX (m);
DELETE (m);
SETPOINTER (p5, m);
ENDSEX (p5);
CLRBR (m);
DELETE (m);
DELETE (m);
Page 433
DO_PAIRS;
DELETE (p5);
DELETE (m);
EVAL;
REMOVE_PAIRS;
end;
procedure NEW_ENV;
begin
FIND (e, env_top);
INSERT (e, env_top);
bara := chr (ord (bara) + 1);
end;
procedure OLD_ENV;
begin
bara := chr (ord (bara) - 1);
FIND (e, env_top);
LEFT (e);
repeat DELETE (e) until OutCM [e] = env_top;
end;
procedure EV; { @[xv[va$...(!x) --> ...a }
begin
DELETE (m);
EVAL;
NEW_ENV;
EVAL;
LEFT (m);
CLRBR (m);
OLD_ENV;
end;
procedure QUOTE; { ('(abc)) --> (abc) }
begin
DELETE (m);
LEFT (m);
CLRBR (m);
end;
procedure EVAL_ATOM; { @[xv...$...x... --> ....v... }
begin
R := OutCM [m];
FIND (e, bara+R);
if OutCM [e] <> #12 then begin
DELETE (m);
COPY (e, m);
end;
end;
Page 434
procedure EVAL_FUNC_ARG; { @[f+$..(f('(ab))).. --> ..a.. }
begin
EVAL;
LEFT (m);
EVAL;
end;
procedure CAR; { (+('(abc))) --> a }
begin
DELETE (m);
EVAL;
if OutCM [m] = '(' then begin
RIGHT (m);
if OutCM [m] = ')' then LEFT (m)
else begin
ENDSEX (m);
while OutCM [m] <> ')' do CLRSEX (m);
BACKSEX (m);
CLRBR (m);
end;
end;
LEFT (m);
CLRBR (m);
end;
procedure CDR; { (-('(abc))) --> (bc) }
begin
DELETE (m);
EVAL;
if OutCM [m] = '(' then begin
RIGHT (m);
if OutCM [m] <> ')' then CLRSEX (m);
LEFT (m); end;
LEFT (m);
CLRBR (m);
end;
procedure CONS; { (*a(bc)) --> (abc) }
begin
DELETE (m);
EVAL;
ENDSEX (m);
EVAL;
if OutCM [m] <> '(' then begin
DELETE (m);
BACKSEX (m);
CLRBR (m); end
else begin
CLRBR (m);
LEFT (m);
Page 435
BACKSEX (m);
LEFT (m);
end;
end;
procedure IF_T_E; { (/1xy) --> x }
begin { (/0xy) --> y }
DELETE (m);
EVAL;
if OutCM [m] = '0' then begin
DELETE (m);
CLRSEX (m);
EVAL;
LEFT (m);
CLRBR (m); end
else begin
DELETE (m);
EVAL;
ENDSEX (m);
CLRSEX (m);
BACKSEX (m);
CLRBR (m);
end;
end;
procedure EQUAL; { (=xx) --> 1 }
var eq: boolean;
begin
DELETE (m);
INSERT (m, '1');
EVAL;
ENDSEX (m);
EVAL;
SETPOINTER (p5, m);
ENDSEX (m);
INSERT (m, '#');
BACKSEX (m);
RIGHT (m);
RIGHT (m);
R := OutCM [m];
INSERT (p5, '#');
eq := false;
while (R = OutCM [p5]) and (R <> '#') do begin
DELETE (m);
R := OutCM [m];
DELETE (p5); end;
if (R = '#') and (OutCM [p5] = '#') then eq := true;
NOOP (p5);
while OutCM [p5] <> '#' do DELETE (p5);
DELETE (p5);
Page 436
NOOP (m);
while OutCM [m] <> '#' do DELETE (m);
DELETE (m);
if not eq then begin
LEFT (m);
DELETE (m);
INSERT (m, '0'); end;
LEFT (m);
LEFT (m);
CLRBR (m);
end;
procedure DISPLAY; { (,('(ab))) --> (ab) }
begin
DELETE (m);
LEFT (m);
CLRBR (m);
EVAL;
end;
procedure EVAL;
begin
if OutCM [m] <> '(' then EVAL_ATOM
else begin
RIGHT (m);
case OutCM [m] of
')': LISTA_VIDA;
'''': QUOTE;
'.': ATOM;
'+': CAR;
'-': CDR;
'*': CONS;
'=': EQUAL;
'/': IF_T_E;
'!': EV;
'&': DEFINE;
',': DISPLAY;
'(': begin
RIGHT (m);
if OutCM [m] = '&' then LAMBDA
else begin
LEFT (m);
EVAL_FUNC_ARG;
end;
end;
else EVAL_FUNC_ARG;
end;
end;
end;
Page 437 begin env_top := '@'; bara := '3'; bara_def := '|'; e := p1; FIND (m, '$'); EVAL; end;
|
|||||||||||||||||