The Relationship Between Propagation Characteristics
and Nonlinearity of Cryptographic Functions
Jennifer Seberry
(The University of Wollongong, Wollongong, NSW 2522, Australia
jennie@cs.uow.edu.au)
Xian-Mo Zhang
(The University of Wollongong, Wollongong, NSW 2522, Australia
xianmo@cs.uow.edu.au)
Yuliang Zheng
(Monash University, Melbourne, VIC 3199, Australia
yzheng@fcit.monash.edu.au)
Abstract:
The connections among the various
nonlinearity criteria is currently an important topic
in the area of designing and analyzing cryptographic functions.
In this paper we show a quantitative relationship
between propagation characteristics and nonlinearity,
two critical indicators of the cryptographic strength of
a Boolean function.
We also present a tight lower bound on the nonlinearity of
a cryptographic function that has propagation characteristics. Keywords:
Cryptography,
Boolean functions,
Encryption functions,
Nonlinearity,
Propagation Characteristics,
SAC,
S-boxes. Category: E.3
1 Introduction
Data Encryption Standard or DES is
a cryptographic algorithm most widely used
by industrial, financial and commercial sectors
all over the world [NBS77].
DES is also the root of many other
data encryption algorithms
proposed in the past decade,
including
LOKI [BKPS93],
FEAL [Miy91]
and
IDEA [LM91][LaSM91][Lai92].
A core component of these encryption algorithms
are the so-called S-boxes or substitution boxes,
each essentially a tuple of nonlinear Boolean functions.
In most cases, these boxes are the only
nonlinear component in an underlying encryption algorithm.
The same can be said with
one-way hashing algorithms
which are commonly employed in the process of
signing and authenticating
electronic messages [ZPS93][Riv92][NIST93].
These all indicate the vital importance of
the design and analysis of
nonlinear cryptographic Boolean functions. Encryption and authentication require
cryptographic (Boolean) functions
with a number of critical properties that
distinguish them from linear (or affine) functions.
Among these properties are
high nonlinearity,
high degree of propagation,
few linear structures,
high algebraic degree etc.
These properties are often called
nonlinearity criteria.
An important topic is to investigate
relationships among the various
nonlinearity criteria.
Progress in this direction has been made Page 136
in [SZZ94d],
where connections have been revealed
among the strict avalanche characteristic,
differential characteristics,
linear structures and nonlinearity,
of quadratic functions. In this paper we carry on
the investigation initiated in [SZZ94d]
and bring together nonlinearity and propagation characteristic
of a function (quadratic or non-quadratic).
These two cryptographic criteria
are seemly quite separate,
in the sense that
the former indicates the minimum distance between a Boolean
function and all the affine functions
whereas the latter
forecasts the avalanche behavior of the function
when some input bits to the function are complemented. In particular we show that
if f, a function on 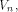 satisfies the propagation criterion with respect to
all but a subset
satisfies the propagation criterion with respect to
all but a subset 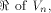 then the nonlinearity of f
satisfies
then the nonlinearity of f
satisfies 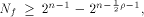
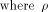 is the maximum dimension
a linear sub-space contained in is the maximum dimension
a linear sub-space contained in 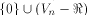 can achieve.
can achieve. We also show that 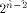 is the tight lower bound
on the nonlinearity of f if f satisfies
the propagation criterion with respect to
at least one vector in is the tight lower bound
on the nonlinearity of f if f satisfies
the propagation criterion with respect to
at least one vector in 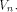 As an immediate consequence,
the nonlinearity of a function that fulfills the
SAC or strict avalanche criterion is
at least
As an immediate consequence,
the nonlinearity of a function that fulfills the
SAC or strict avalanche criterion is
at least 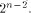 Two techniques are employed in the proofs of
our main results.
The first technique is in regard to the structure of
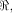 the set of vectors where
the function f does not satisfy the propagation criterion.
By considering
a linear sub-space
with the maximum dimension
contained in the set of vectors where
the function f does not satisfy the propagation criterion.
By considering
a linear sub-space
with the maximum dimension
contained in 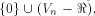 together with its complementary sub-space,
we will be able to identify how the vectors in
together with its complementary sub-space,
we will be able to identify how the vectors in 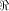 are distributed.
The second technique is based on
a novel idea of refining
Parseval's equation, a well-known relationship
in the theory of orthogonal transforms.
A combination of these two techniques
together with some careful analyses
proves to be a powerful tool
in examining the relationship
among nonlinearity criteria.
are distributed.
The second technique is based on
a novel idea of refining
Parseval's equation, a well-known relationship
in the theory of orthogonal transforms.
A combination of these two techniques
together with some careful analyses
proves to be a powerful tool
in examining the relationship
among nonlinearity criteria. The organization of the rest of the paper is as follows:
Section 2
introduces basic notations and conventions,
while Section 3
presents background information on
the Walsh-Hadamard transform.
The distribution of vectors
where the propagation criterion is not satisfied
is discussed in Section 4.
This result is employed in Section 5
where a quantitative relationship between
nonlinearity and propagation characteristics is derived.
This relationship is further developed
in Section 6
to identify a tight lower bound on
nonlinearity of functions with propagation characteristics.
The paper is closed by some concluding remarks
in Section 7.
2 Basic Definitions
We consider Boolean functions from 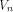 to GF(2)
(or simply functions on to GF(2)
(or simply functions on 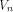 ), ),
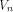 is the vector space of n tuples of elements from GF(2).
The truth table of a function f on is the vector space of n tuples of elements from GF(2).
The truth table of a function f on 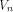 is a (0,1)-sequence defined by
is a (0,1)-sequence defined by 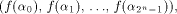 and the sequence of f
is a (1,-1)-sequence defined by
and the sequence of f
is a (1,-1)-sequence defined by 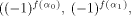
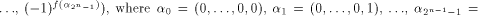 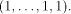 The matrix of f is a (1,-1)-matrix of order
The matrix of f is a (1,-1)-matrix of order 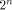 defined by defined by 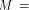 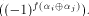 f is said to be balanced if its truth table contains an equal number of
ones and zeros.
f is said to be balanced if its truth table contains an equal number of
ones and zeros. An affine function f on 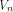 is a function
that takes the form of is a function
that takes the form of 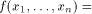 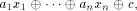 where where 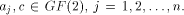 Furthermore f is called a linear function if c=0.
Furthermore f is called a linear function if c=0. Page 137
Definition 1.
The Hamming weight of a (0,1)-sequence s, denoted by 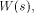 is the number of ones in the sequence.
Given two functions f and g on
is the number of ones in the sequence.
Given two functions f and g on 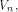 the Hamming distance d(f,g)
between them is defined as
the Hamming weight of the truth table of
f(x)
the Hamming distance d(f,g)
between them is defined as
the Hamming weight of the truth table of
f(x)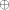 g(x),
where g(x),
where 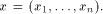 d.
The nonlinearity of f, denoted by d.
The nonlinearity of f, denoted by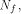 is the minimal Hamming distance
between f and all affine functions on
is the minimal Hamming distance
between f and all affine functions on 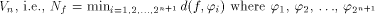 are all the affine functions on
are all the affine functions on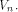 Note that
the maximum nonlinearity of functions on 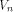 coincides with the covering radius of the first order
binary Reed-Muller code RM(1,n) of length
coincides with the covering radius of the first order
binary Reed-Muller code RM(1,n) of length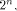 which is bounded from above by
which is bounded from above by 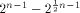 (see for instance [CKHFMS85]).
Hence
(see for instance [CKHFMS85]).
Hence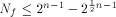 for any function on
for any function on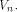 Next we introduce the definition of propagation criterion.
Next we introduce the definition of propagation criterion. Definition 2.
Let f be a function on 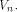 We say that f satisfies
We say that f satisfies 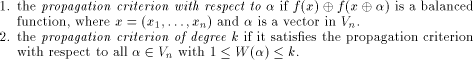
f(x) 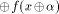 is also called
the directional derivative of f in the direction is also called
the directional derivative of f in the direction  .
The above definition for propagation criterion
is from [PLL91].
Further work on the topic can be found in [PGV91].
Note that the strict avalanche criterion (SAC) introduced by Webster and
Tavares [Web85],[WT86] is equivalent to the
propagation criterion of degree 1 and
that the perfect nonlinearity studied by Meier and Staffelbach [MS90]
is equivalent to the propagation criterion of degree n where n is the number
of the coordinates of the function. .
The above definition for propagation criterion
is from [PLL91].
Further work on the topic can be found in [PGV91].
Note that the strict avalanche criterion (SAC) introduced by Webster and
Tavares [Web85],[WT86] is equivalent to the
propagation criterion of degree 1 and
that the perfect nonlinearity studied by Meier and Staffelbach [MS90]
is equivalent to the propagation criterion of degree n where n is the number
of the coordinates of the function. While the propagation characteristic measures
the avalanche effect of a function,
the linear structure is a concept that in a sense
complements the former,
namely, it indicates the straightness of a function. Definition 3.
Let f be a function on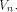 A vector
A vector 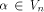 is called a
linear structure of f if is called a
linear structure of f if 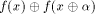 is a constant. is a constant. By definition,
the zero vector in 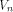 is
a linear structure of all functions on is
a linear structure of all functions on 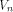 It is not hard to see that
the linear structures of a function f
form a linear sub-space of
It is not hard to see that
the linear structures of a function f
form a linear sub-space of 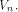 The dimension of the sub-space is called
the linearity dimension of f.
We note that it was Evertse
who first introduced the notion of linear structure
(in a sense broader than ours)
and studied its implication on
the security of encryption algorithms [Eve88].
The dimension of the sub-space is called
the linearity dimension of f.
We note that it was Evertse
who first introduced the notion of linear structure
(in a sense broader than ours)
and studied its implication on
the security of encryption algorithms [Eve88]. A (1,-1)-matrix H of order m is called a Hadamard matrix
if 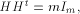 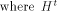 is the transpose of H
and is the transpose of H
and 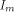 is the identity matrix of order m.
A Sylvester-Hadamard matrix of order is the identity matrix of order m.
A Sylvester-Hadamard matrix of order 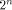 , denoted by , denoted by 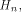 is generated by the following recursive relation
is generated by the following recursive relation 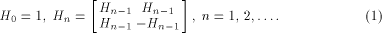
Let 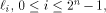 be the i row of
be the i row of 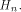 By Lemma 2 of [SZZ94a],
By Lemma 2 of [SZZ94a],
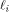 is the sequence of a linear function is the sequence of a linear function 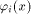 defined by the scalar product
defined by the scalar product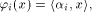 where
where 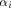 is the ith vector in is the ith vector in 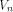 according to the ascending order.
according to the ascending order. Page 138
Definition 4.
Let f be a function on 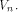 The Walsh-Hadamard transform
of f is defined as
The Walsh-Hadamard transform
of f is defined as 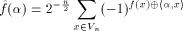
where 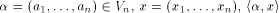 is the scalar product of
is the scalar product of 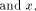 namely
namely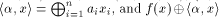 ,
is regarded as a real-valued function. ,
is regarded as a real-valued function. The Walsh-Hadamard transform,
also called the discrete Fourier transform,
has numerous applications in areas
ranging from physical science to communications engineering.
It appears in several slightly different forms [Rot76],[MS77],[Dil72].
The above definition follows the line in [Rot76].
It can be equivalently written as 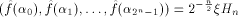
where 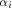 is the ith vector in is the ith vector in 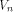 according to the ascending order
according to the ascending order 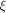 ,
is the sequence of f
and ,
is the sequence of f
and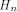 is the Sylvester-Hadamard matrix of order is the Sylvester-Hadamard matrix of order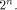 Definition 5.
A function f on 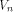 is called a bent function if
its Walsh-Hadamard transform satisfies is called a bent function if
its Walsh-Hadamard transform satisfies 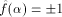
for all 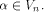 Bent functions can be characterized in various
ways [AT90],[Dil72],[SZZ94a],[YH89].
In particular the following four statements are equivalent: 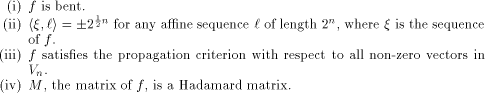
Bent functions on 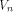 exist only when n is even [Rot76].
Another important property of bent functions is
that they achieve the highest possible
nonlinearity exist only when n is even [Rot76].
Another important property of bent functions is
that they achieve the highest possible
nonlinearity 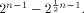
3 More on Walsh-Hadamard transform and Nonlinearity
As the Walsh-Hadamard transform plays a key role
in the proofs of main results to be described
in the following sections,
this section provides some background knowledge
on the transform.
More information regarding the transform can be
found in [MS77],[Dil72].
In addition, Beauchamp's book [Bea84]
is a good source of information on other related orthogonal transforms
with their applications. Given two sequences 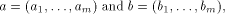 their component-wise product is defined by
their component-wise product is defined by 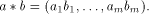 Let f be a function on
Let f be a function on 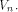 For a vector
For a vector 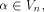 denote by
denote by 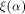 the sequence of the sequence of 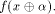 Thus
Thus 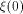 is the sequence of f itself
and is the sequence of f itself
and 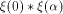 is the sequence of is the sequence of 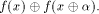 Page 139
Set 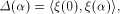
the scalar product of 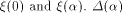 is also called
the auto-correlation of f with a shift is also called
the auto-correlation of f with a shift  .
Obviously, .
Obviously, 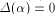 if and only if if and only if 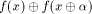 is balanced,
i.e., f satisfies the propagation criterion with respect to is balanced,
i.e., f satisfies the propagation criterion with respect to 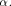 On the other hand, if
On the other hand, if 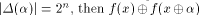 is a constant
and hence is a constant
and hence  is a linear structure of f. is a linear structure of f. Let 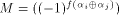 be the matrix of f and
be the matrix of f and 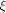 be the sequence of f.
Due to a very pretty result by R. L. McFarland
(cf. Theorem 3.3 of [Dil72]),
M can be decomposed into be the sequence of f.
Due to a very pretty result by R. L. McFarland
(cf. Theorem 3.3 of [Dil72]),
M can be decomposed into 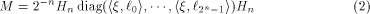
where 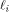 is the ith row of is the ith row of 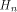 , a Sylvester-Hadamard matrix of order , a Sylvester-Hadamard matrix of order 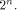 Clearly 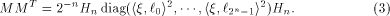
On the other hand, we always have 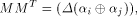
where 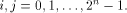 Comparing the two sides of (3), we have 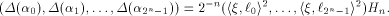
Equivalently we write 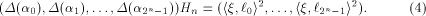
In engineering, (4) is better known
as (a special form of) the Wiener-Khintchine Theorem [Bea84].
A closely related result is
Parseval's equation (Corollary 3, p. 416 of [MS77]) 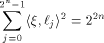
which also holds for any function f on 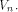 Let S be a set of vectors in 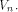 The rank of S is the maximum number of linearly independent vectors in S.
Note that when S forms a linear sub-space of
The rank of S is the maximum number of linearly independent vectors in S.
Note that when S forms a linear sub-space of 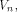 its rank coincides with its dimension.
its rank coincides with its dimension. The distance between two functions
can be expressed as 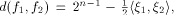 where
where 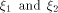 are the sequences of are the sequences of 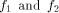 respectively.
(For a proof see for instance Lemma 6 of [SZZ94a].)
Immediately we have:
respectively.
(For a proof see for instance Lemma 6 of [SZZ94a].)
Immediately we have: Lemma 6.
The nonlinearity of a function f on 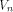 can be calculated by can be calculated by 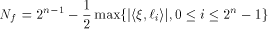
where 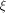 is the sequence of f and is the sequence of f and
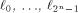 are the rows of are the rows of 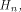 namely, the sequences of the linear functions on
namely, the sequences of the linear functions on 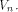 Page 140
The next lemma regarding splitting
the power of 2 can be found in [SZZ94d] Lemma 7.
Let 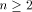 be a positive integer and be a positive integer and 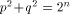 where both where both
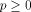 and and 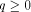 are integers. Then are integers. Then 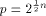 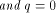 when n is even, and
when n is even, and 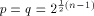 when n is odd. when n is odd. In the next section we examine
the distribution of the vectors in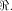
4 Distribution of 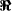
Let f be a function on 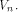 Assume that f satisfies the propagation criterion with respect
to all but a subset
Assume that f satisfies the propagation criterion with respect
to all but a subset 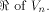 Note that
Note that 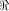 always contains the zero vector 0.
Write always contains the zero vector 0.
Write 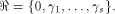 Thus Thus 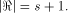 Set 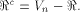 Then f satisfies the propagation criterion with
respect to all vectors in
Then f satisfies the propagation criterion with
respect to all vectors in 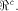 Consider the set of vectors 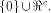 Then
Then 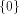 is a linear sub-space contained in is a linear sub-space contained in 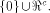 When
When 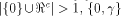 is a linear sub-space
for any nonzero vector in is a linear sub-space
for any nonzero vector in 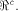 We are particularly interested in linear sub-spaces
with the maximum dimension contained in
We are particularly interested in linear sub-spaces
with the maximum dimension contained in 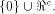 For convenience, denote by
For convenience, denote by  the maximum dimension
and by W a linear sub-space in the maximum dimension
and by W a linear sub-space in 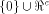 that achieves the maximum dimension.
that achieves the maximum dimension. Obviously, f is bent if and only if 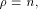 and f does not satisfy the propagation criterion with
respect to any vector if and only if
and f does not satisfy the propagation criterion with
respect to any vector if and only if 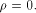 The case when
The case when 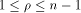 is especially interesting.
is especially interesting. Now let U be a complementary sub-space of W,
namely 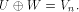 Then each vector
Then each vector 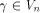 can be
uniquely expressed as can be
uniquely expressed as 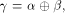 where
where 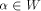 and and 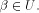 As the dimension of W is
As the dimension of W is 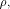 the dimension of U is equal to
the dimension of U is equal to 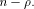 Write
Write 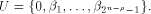 Proposition 8.
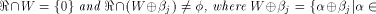
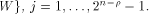 Proof.
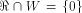 follows from the fact that
W is a sub-space of follows from the fact that
W is a sub-space of 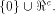 Next we consider
Next we consider 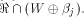 Clearly, 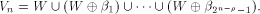
In addition, 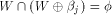
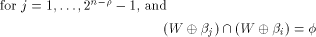
for any 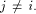 Assume for contradiction that Assume for contradiction that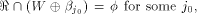 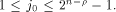 Then we have
Then we have 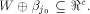 In this case
In this case 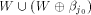 must form a sub-space of
must form a sub-space of 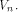 This contradicts the definition that
W is a linear sub-space with the maximum dimension in
This contradicts the definition that
W is a linear sub-space with the maximum dimension in 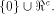 This completes the proof. This completes the proof. The next corollary follows directly from the above proposition. Corollary 9.
The size of 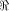 satisfies satisfies
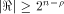 and
hence the rank of and
hence the rank of 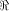 is at least is at least 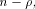 where
where  is the maximum dimension
a linear sub-space in is the maximum dimension
a linear sub-space in 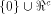 can achieve. can achieve. Page 141
5 Relating Nonlinearity to Propagation Characteristics
We proceed to the discussion of the nonlinearity of f. The main difficulty lies in
finding a good approximation of 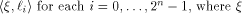 is the sequence of f and
is the sequence of f and
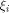 is a row of is a row of 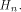 First we assume that 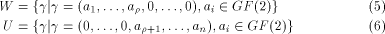
where W is a linear sub-space
in 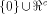 that achieves the maximum dimension
that achieves the maximum dimension  and
U is a complementary sub-space of W.
The more general case where
(5) or (6) is not satisfied
can be dealt with after employing
a nonsingular transform on the input of f.
This will be discussed in the later part of this section.
and
U is a complementary sub-space of W.
The more general case where
(5) or (6) is not satisfied
can be dealt with after employing
a nonsingular transform on the input of f.
This will be discussed in the later part of this section. Recall that 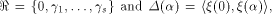 where
where 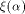 is the sequence of is the sequence of 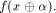 Since Since 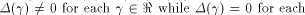
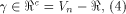 is specialized as is specialized as 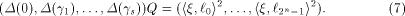
where 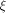 is the sequence of f, is the sequence of f,
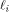 is the ith row of is the ith row of 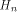 and Q comprises the 0th,
and Q comprises the 0th, 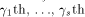 rows of rows of 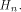 Note that Q is an
Note that Q is an 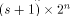 matrix. matrix. Let 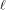 be the be the 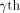 row of row of 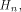 where
where 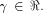 Note that
Note that  can be uniquely expressed as can be uniquely expressed as 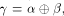 where
where 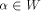 and and 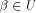 .
Let .
Let 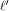 be the be the 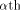 row of row of 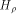 and and
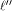 be the be the 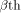 row of row of 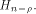 As
As
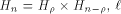 can be represented by can be represented by 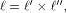 where
where  denotes the Kronecker product. denotes the Kronecker product. From the construction of
we can see that the 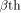 row of row of 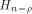 is an all-one sequence of length
if
and a balanced (1,-1)-sequence of length
is an all-one sequence of length
if
and a balanced (1,-1)-sequence of length 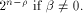 Recall that 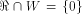 (see also Proposition 8).
There are two cases associated with
(see also Proposition 8).
There are two cases associated with 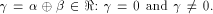 In the first case,
In the first case, 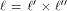 is the all-one sequence of length
is the all-one sequence of length 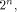 while in the second case,
we have
while in the second case,
we have 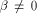 which implies that
which implies that
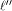 is a balanced (1,-1)-sequence of length is a balanced (1,-1)-sequence of length 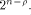 and hence
and hence 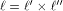 is a concatenation of
is a concatenation of 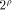 balanced (1,-1)-sequences of length balanced (1,-1)-sequences of length 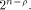 Therefore we can write 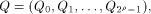 where each
where each 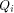 is a (1,-1)-matrix of
order is a (1,-1)-matrix of
order 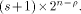 It is important to note that
the top row of each
It is important to note that
the top row of each 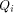 is
the all-one sequence,
while the rest are
balanced (1,-1)-sequences of length is
the all-one sequence,
while the rest are
balanced (1,-1)-sequences of length 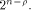 With 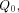 we have we have 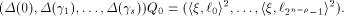
Let 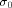 be the all-one sequence of length be the all-one sequence of length 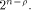 Then Then 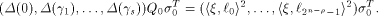
This causes 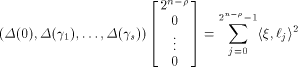
Page 142
and 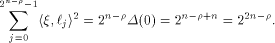
Similarly, with 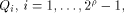 we have we have 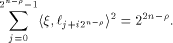
Thus we have the following result: Lemma 10.
Assume that f, a function on 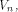 satisfies the propagation criterion with respect
to all but a subset
satisfies the propagation criterion with respect
to all but a subset 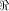 of vectors in of vectors in 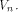 Set
Set 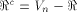 and let W be a linear sub-space with the maximum dimension
and let W be a linear sub-space with the maximum dimension 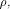 in
in 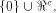 and U be a complementary sub-space of W.
Assume that W and U satisfy (5) and (6)
respectively.
Then
and U be a complementary sub-space of W.
Assume that W and U satisfy (5) and (6)
respectively.
Then 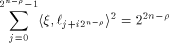
for all 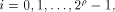 where
where
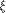 is the sequence of f and
each is the sequence of f and
each 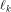 is a row of is a row of 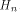 Lemma 10 can be viewed as a refinement of
Parseval's equation 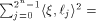
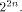 It implies that
It implies that 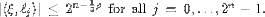 Therefore by Lemma 6 we have
Therefore by Lemma 6 we have 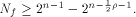
So far we have assumed that
W and U satisfy (5) and (6)
respectively.
When this is not the case,
we can always find a nonsingular 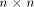 matrix A whose entries are from GF(2)
such that
the sub-spaces W' and U' associated with
f'(x) = f(x A) have the required forms.
f' and f have the same algebraic degree
and nonlinearity (see Lemma 10 of [SZZ94b]).
This shows that the following theorem is true.
matrix A whose entries are from GF(2)
such that
the sub-spaces W' and U' associated with
f'(x) = f(x A) have the required forms.
f' and f have the same algebraic degree
and nonlinearity (see Lemma 10 of [SZZ94b]).
This shows that the following theorem is true. Theorem 11.
For any function on 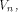 the nonlinearity of f
satisfies
the nonlinearity of f
satisfies 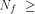 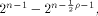 where
where  is the maximum dimension of the linear
sub-spaces in is the maximum dimension of the linear
sub-spaces in 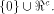 Theorem 11 indicates that
the nonlinearity of a function
is determined by the maximum dimension
that a linear sub-spaces in 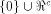 can achieve,
but not by the size of can achieve,
but not by the size of  In [SZZ94e], we have proved that 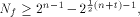 where t is the rank of
where t is the rank of 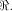 By Corollary 9, we have
By Corollary 9, we have 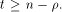 This implies that
This implies that 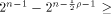
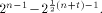 Thus Theorem 11
is an improvement to the result in [SZZ94e].
This improvement can be demonstrated by a concrete example.
In [SZZ94e],
the following function on
Thus Theorem 11
is an improvement to the result in [SZZ94e].
This improvement can be demonstrated by a concrete example.
In [SZZ94e],
the following function on 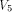 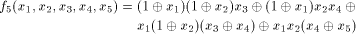
Page 143
has been shown to satisfy the propagation criterion with respect
to all but the following fives vectors in 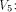 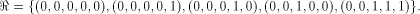
The rank t of 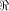 is equal to 3.
By using the result of [SZZ94e], is equal to 3.
By using the result of [SZZ94e],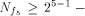
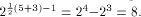 On the other hand,
we can set
On the other hand,
we can set 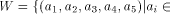
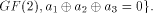 W is a four-dimensional sub-space in
W is a four-dimensional sub-space in 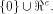 Using Theorem 11 with  =4, we have =4, we have 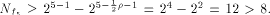 (Note that according to [CKHFMS85],
the maximum nonlinearity a function on
(Note that according to [CKHFMS85],
the maximum nonlinearity a function on 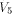 can achieve is 12.
Hence we have can achieve is 12.
Hence we have 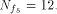 ) )
6 A Tight Lower Bound on Nonlinearity of Functions with Propagation Characteristics
By Theorem 11, 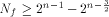 if f, a function on if f, a function on 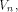 satisfies the propagation criterion
with respect to at least one vector in
satisfies the propagation criterion
with respect to at least one vector in 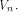 This section shows that this lower bound can be significantly improved.
Indeed we prove that
This section shows that this lower bound can be significantly improved.
Indeed we prove that 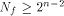 and also show that it is tight. and also show that it is tight. Theorem 12.
If f, a function on 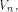 satisfies the propagation criterion with respect to
one or more vectors in
satisfies the propagation criterion with respect to
one or more vectors in 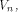 then the nonlinearity of f satisfies
then the nonlinearity of f satisfies 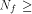
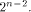 Proof.
As in the previous sections,
we denote by 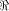 the set of vectors in the set of vectors in 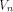 with respect to which the propagation criterion
is not satisfied by f.
We also let
with respect to which the propagation criterion
is not satisfied by f.
We also let 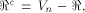 and W be a linear sub-space
in
and W be a linear sub-space
in 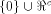 that achieves the maximum dimension that achieves the maximum dimension 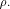 By Theorem 11,
the theorem is trivially true when 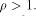 Next we consider the case when
Next we consider the case when 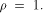 We prove this part by further refining
the Parseval's equation.
We prove this part by further refining
the Parseval's equation. As in the proof of Lemma 10,
without loss of generality, we can assume that 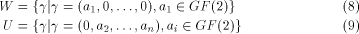
Similarly to Lemma 10, we have 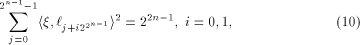
where 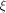 is the sequence of f and is the sequence of f and 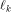 is a row of is a row of 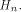 Comparing the first row of (2), we have 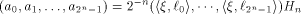
or equivalently, 
Page 144
where each 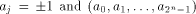 is the first row of the matrix M described in (2).
is the first row of the matrix M described in (2). Rewrite 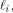 the ith row of the ith row of 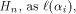 where
where 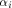 is the binary representation of an integer i
in the ascending alphabetical order.
Set is the binary representation of an integer i
in the ascending alphabetical order.
Set 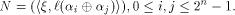
N is a symmetric matrix of order 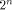 with integer entries.
In [Rot76],
Rothaus has shown that with integer entries.
In [Rot76],
Rothaus has shown that 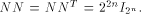 We can split N into four sub-matrices of equal size,
namely
We can split N into four sub-matrices of equal size,
namely 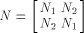
where each 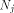 is a matrix of order is a matrix of order 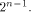 As
As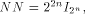 we have
we have 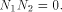 Let 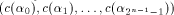 be an
arbitrary linear sequence of length be an
arbitrary linear sequence of length 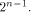 Then 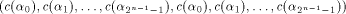
is a linear sequence of length 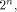 and hence a row of
and hence a row of 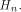 Thus from (11), we have
Thus from (11), we have 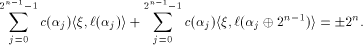
Hence 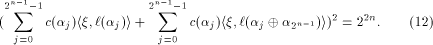
Rewrite the left hand side of (12) as 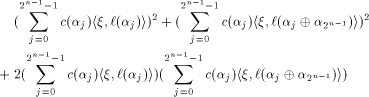
where 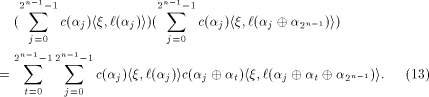
As 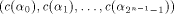 is a linear sequence,
is a linear sequence, 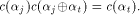 Hence (13) can be written as 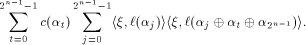
Page 145
Since 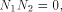 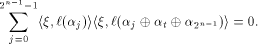
This proves that (13) is equal to zero and
hence 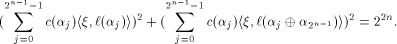
By Lemma 7, 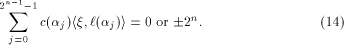
Since 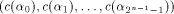 is an arbitrary
linear sequence of length is an arbitrary
linear sequence of length 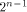 and each linear sequence of length and each linear sequence of length 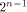 is a column of is a column of 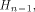 from (14) we have from (14) we have 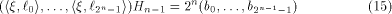
where 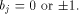 Therefore Therefore 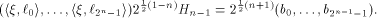
Recall that a matrix A of order s is said to be orthogonal if 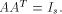 It is easy to verify that It is easy to verify that 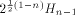 is an orthogonal matrix. Thus is an orthogonal matrix. Thus 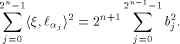
On the other hand, by (10) we have 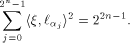
Hence 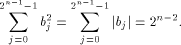
Now let 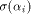 denote the ith row of denote the ith row of 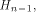 where
where 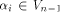 is the binary representation of is the binary representation of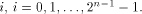 From (15), From (15), 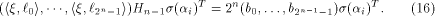
Note that 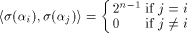
Page 146
Thus 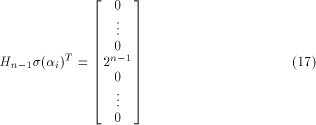
where 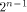 is on the ith position of the column vector. is on the ith position of the column vector. Write 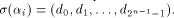 Then Then 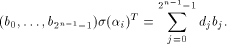
As 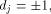 we have we have 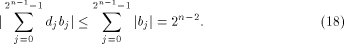
From (16), (17) and (18) 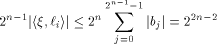
and hence 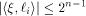
where i is an arbitrary integer in 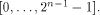 Similarly,
Similarly, 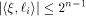
holds for all 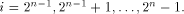 By Lemma 6, the nonlinearity of f satisfies
By Lemma 6, the nonlinearity of f satisfies 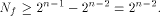
This completes the proof. As an immediate consequence, we have Corollary 13.
Let f be a function on 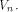 Then the following statements hold: Then the following statements hold: 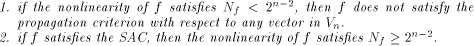
Page 147
Finally we show that
the lower bound 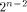 is tight.
We achieve the goal
by demonstrating a function on is tight.
We achieve the goal
by demonstrating a function on 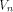 whose nonlinearity
is equal to whose nonlinearity
is equal to 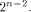 Let
Let 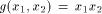 be
a function on be
a function on 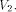 Then the nonlinearity of g is
Then the nonlinearity of g is 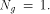 Now let
Now let
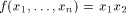 be
a function on be
a function on 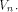 Then the nonlinearity of f is
Then the nonlinearity of f is 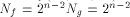 (see for instance Lemma 8 of [SZZ94c]).
f satisfies the propagation criterion
with respect to
all vectors in
(see for instance Lemma 8 of [SZZ94c]).
f satisfies the propagation criterion
with respect to
all vectors in 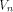 whose first two bits are nonzero,
which count for three quarters of the vectors in whose first two bits are nonzero,
which count for three quarters of the vectors in 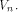 It is not hard to verify that
It is not hard to verify that 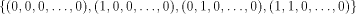
is the linear sub-space that achieves the maximum dimension 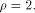 Thus we have a result described as follows: Thus we have a result described as follows: Lemma 14.
The lower bound 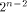 as stated in Theorem 12 is tight. as stated in Theorem 12 is tight.
7 Conclusion
We have shown quantitative relationships
between
nonlinearity, propagation characteristics and the SAC.
A tight lower bound on the nonlinearity of
a function with propagation characteristics
is also presented. This research has also introduced a number of
interesting problems yet to be resolved.
One of the problems is regarding the
size and distribution of 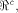 the set of vectors where the propagation criterion
is satisfied by a function on
the set of vectors where the propagation criterion
is satisfied by a function on 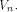 For all the functions we know of,
For all the functions we know of,
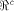 is either an empty set
or a set with at least is either an empty set
or a set with at least 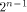 vectors.
We believe that
any further understanding of this problem
will contribute to
the research into
the design and analysis of
cryptographically strong
nonlinear functions. vectors.
We believe that
any further understanding of this problem
will contribute to
the research into
the design and analysis of
cryptographically strong
nonlinear functions. Acknowledgments We would like to thank the anonymous referees for their
helpful comments.
The first author was supported in part by
the Australian Research Council (ARC)
under the reference numbers
A49130102, A49131885 and A49232172,
and
by the Australian Telecommunications and Electronics Research Board (ATERB)
under the reference number C010/058,
the second author by
ARC A49130102
and ATERB C010/058,
and the third author
by ARC A49232172 and ATERB N069/412.
All authors were supported by
a University of Wollongong Research Program grant. This work was done while the third author
was with the University of Wollongong.
References
[AT90]
C. M. Adams and S. E. Tavares.
Generating and counting binary bent sequences.
IEEE Transactions on Information Theory, IT-36 No.
5:1170-1173, 1990. Page 148
[Bea84]
K. G. Beauchamp.
Applications of Walsh and Related Functions with an Introduction
to Sequency Functions.
Microelectronics and Signal Processing. Academic Press, London, New
York, Tokyo, 1984.
[BKPS93]
L. Brown, M. Kwan, J. Pieprzyk, and J. Seberry.
Improving resistance to differential cryptanalysis and the redesign
of LOKI.
In Advances in
Cryptology - ASIACRYPT'91,
Lecture Notes in Computer Science,
vol. 739,
pp. 6-50,
Springer-Verlag, Berlin, New York, Tokyo, 1993.
[CKHFMS85]
G. D. Cohen, M. G. Karpovsky, Jr. H. F. Mattson, and J. R. Schatz.
Covering radius --- survey and recent results.
IEEE Transactions on Information Theory, IT-31(3):328-343,
1985.
[Dil72]
J. F. Dillon.
A survey of bent functions.
The NSA Technical Journal, pp. 191-215, 1972.
(unclassified).
[Eve88]
J.-H. Evertse.
Linear structures in blockciphers.
In Advances in Cryptology - EUROCRYPT'87,
Lecture Notes in Computer Science,
vol. 304, pp. 249-266,
Springer-Verlag, Berlin, Heidelberg, New York, 1988.
[Lai92]
X. Lai.
On the Design and Security of Block Ciphers.
ETH Series in Information Processing. Hartung-Gorre Verlag Konstanz,
Zuerich, 1992.
[LaSM91]
X. Lai and J. L. Massey ans S. Murphy.
Markov ciphers and differential cryptanalysis.
In D. W. Davies, editor, Advances in Cryptology - EUROCRYPT'91,
Lecture Notes in Computer Science,
vol. 547,
pp. 17-38,
Springer-Verlag, Berlin, New York, Tokyo, 1991.
[LM91]
X. Lai and J. L. Massey.
A proposal for a new block encryption standard.
In I. B. Damgard, editor, Advances in Cryptology -
EUROCRYPT'90,
Lecture Notes in Computer Science,
vol. 473,
pp. 389-404,
Springer-Verlag, Berlin, New York, Tokyo, 1991.
[Miy91]
S. Miyaguchi.
The FEAL cipher family.
In Advances in Cryptology - CRYPTO'90,
Lecture Notes in Computer Science,
vol. 537,
pp. 627-638,
Springer-Verlag, Berlin, New York, Tokyo, 1991.
[MS77]
F. J. MacWilliams and N. J. A. Sloane.
The Theory of Error-Correcting Codes.
North-Holland, Amsterdam, New York, Oxford, 1977.
[MS90]
W. Meier and O. Staffelbach.
Nonlinearity criteria for cryptographic functions.
In Advances in Cryptology - EUROCRYPT'89,
Lecture Notes in Computer Science,
vol. 434,
pp. 549-562,
Springer-Verlag, Berlin, Heidelberg, New York, 1990.
[NBS77]
National Bureau of Standards.
Data encryption standard.
Federal Information Processing Standards Publication FIPS PUB 46,
U.S. Department of Commerce, January 1977.
[NIST93]
National Institute of Standards and Technology.
Secure hash standard.
Federal Information Processing Standards Publication FIPS PUB 180,
U.S. Department of Commerce, May 1993.
[PGV91]
B. Preneel, R. Govaerts, and J. Vandewalle.
Boolean functions satisfying higher order propagation criteria.
In Advances in Cryptology - EUROCRYPT'91,
Lecture Notes in Computer Science,
vol. 547,
pp. 141-152,
Springer-Verlag, Berlin, Heidelberg, New York, 1991.
[PLL91]
B. Preneel, W. V. Leekwijck, L. V. Linden, R. Govaerts, and J. Vandewalle.
Propagation characteristics of boolean functions.
In Advances in Cryptology - EUROCRYPT'90,
Lecture Notes in Computer Science,
vol. 437,
pp. 155-165,
Springer-Verlag, Berlin, Heidelberg, New York, 1991.
[Riv92]
R. Rivest.
The MD5 message digest algorithm, April 1992.
Request for Comments (RFC) 1321.
[Rot76]
O. S. Rothaus.
On ``bent'' functions.
Journal of Combinatorial Theory, Ser. A, 20:300-305, 1976.
[SZZ94a]
J. Seberry, X. M. Zhang, and Y. Zheng.
Nonlinearity and propagation characteristics of balanced boolean
functions.
To appear in Information Page 149
and Computation, 1994.
[SZZ94b]
J. Seberry, X. M. Zhang, and Y. Zheng.
Nonlinearly balanced boolean functions and their propagation
characteristics.
In Advances in Cryptology - CRYPTO'93,
Lecture Notes in Computer Science,
vol. 773,
pp. 49-60,
Springer-Verlag, Berlin, Heidelberg, New York, 1994.
[SZZ94c]
J. Seberry, X. M. Zhang, and Y. Zheng.
On constructions and nonlinearity of correlation immune functions.
In Advances in Cryptology - EUROCRYPT'93,
Lecture Notes in Computer Science,
vol. 765,
pp. 181-199,
Springer-Verlag, Berlin, Heidelberg, New York, 1994.
[SZZ94d]
J. Seberry, X. M. Zhang, and Y. Zheng.
Relationships among nonlinearity criteria.
Presented at EUROCRYPT'94, 1994.
[SZZ94e]
J. Seberry, X. M. Zhang, and Y. Zheng.
Structures of cryptographic functions with strong avalanche
characteristics.
Presented at ASIACRYPT'94, 1994.
[Web85]
A. F. Webster.
Plaintext/ciphertext bit dependencies in cryptographic system.
Master's Thesis, Department of Electrical Engineering, Queen's
University, Ontario, Cannada, 1985.
[WT86]
A. F. Webster and S. E. Tavares.
On the design of S-boxes.
In Advances in Cryptology - CRYPTO'85,
Lecture Notes in Computer Science,
vol. 219,
pp. 523-534,
Springer-Verlag, Berlin, Heidelberg, New York, 1986.
[YH89]
R. Yarlagadda and J. E. Hershey.
Analysis and synthesis of bent sequences.
IEE Proceedings (Part E), 136:112-123, 1989.
[ZPS93]
Y. Zheng, J. Pieprzyk, and J. Seberry.
HAVAL --- a one-way hashing algorithm with varialbe length of
output.
In Advances in Cryptology - AUSCRYPT'92,
Lecture Notes in Computer Science,
vol. 718,
pp. 83-104,
Springer-Verlag, Berlin, New York, Tokyo, 1993. Page 150
|
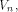 satisfies the propagation criterion with respect to
all but a subset
satisfies the propagation criterion with respect to
all but a subset 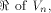 then the nonlinearity of f
satisfies
then the nonlinearity of f
satisfies 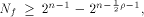
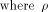 is the maximum dimension
a linear sub-space contained in
is the maximum dimension
a linear sub-space contained in 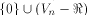 can achieve.
can achieve.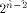 is the tight lower bound
on the nonlinearity of f if f satisfies
the propagation criterion with respect to
at least one vector in
is the tight lower bound
on the nonlinearity of f if f satisfies
the propagation criterion with respect to
at least one vector in 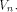 As an immediate consequence,
the nonlinearity of a function that fulfills the
SAC or strict avalanche criterion is
at least
As an immediate consequence,
the nonlinearity of a function that fulfills the
SAC or strict avalanche criterion is
at least 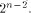
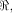 the set of vectors where
the function f does not satisfy the propagation criterion.
By considering
a linear sub-space
with the maximum dimension
contained in
the set of vectors where
the function f does not satisfy the propagation criterion.
By considering
a linear sub-space
with the maximum dimension
contained in 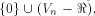 together with its complementary sub-space,
we will be able to identify how the vectors in
together with its complementary sub-space,
we will be able to identify how the vectors in 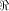 are distributed.
The second technique is based on
a novel idea of refining
Parseval's equation, a well-known relationship
in the theory of orthogonal transforms.
A combination of these two techniques
together with some careful analyses
proves to be a powerful tool
in examining the relationship
among nonlinearity criteria.
are distributed.
The second technique is based on
a novel idea of refining
Parseval's equation, a well-known relationship
in the theory of orthogonal transforms.
A combination of these two techniques
together with some careful analyses
proves to be a powerful tool
in examining the relationship
among nonlinearity criteria.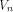 to GF(2)
(or simply functions on
to GF(2)
(or simply functions on 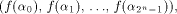 and the sequence of f
is a (1,-1)-sequence defined by
and the sequence of f
is a (1,-1)-sequence defined by 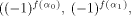
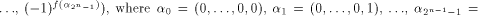
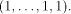 The matrix of f is a (1,-1)-matrix of order
The matrix of f is a (1,-1)-matrix of order 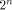 defined by
defined by 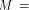
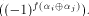 f is said to be balanced if its truth table contains an equal number of
ones and zeros.
f is said to be balanced if its truth table contains an equal number of
ones and zeros.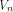 is a function
that takes the form of
is a function
that takes the form of 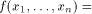
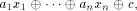 where
where 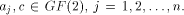 Furthermore f is called a linear function if c=0.
Furthermore f is called a linear function if c=0.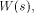 is the number of ones in the sequence.
Given two functions f and g on
is the number of ones in the sequence.
Given two functions f and g on 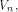 the Hamming distance d(f,g)
between them is defined as
the Hamming weight of the truth table of
f(x)
the Hamming distance d(f,g)
between them is defined as
the Hamming weight of the truth table of
f(x)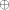 g(x),
where
g(x),
where 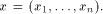 d.
The nonlinearity of f, denoted by
d.
The nonlinearity of f, denoted by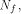 is the minimal Hamming distance
between f and all affine functions on
is the minimal Hamming distance
between f and all affine functions on 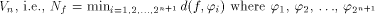 are all the affine functions on
are all the affine functions on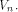
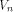 coincides with the covering radius of the first order
binary Reed-Muller code RM(1,n) of length
coincides with the covering radius of the first order
binary Reed-Muller code RM(1,n) of length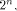 which is bounded from above by
which is bounded from above by 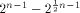 (see for instance [
(see for instance [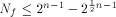 for any function on
for any function on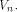 Next we introduce the definition of propagation criterion.
Next we introduce the definition of propagation criterion.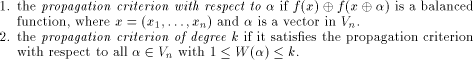
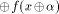 is also called
the directional derivative of f in the direction
is also called
the directional derivative of f in the direction  .
The above definition for propagation criterion
is from [
.
The above definition for propagation criterion
is from [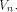 A vector
A vector 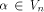 is called a
linear structure of f if
is called a
linear structure of f if 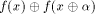 is a constant.
is a constant.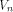 is
a linear structure of all functions on
is
a linear structure of all functions on 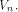 The dimension of the sub-space is called
the linearity dimension of f.
We note that it was Evertse
who first introduced the notion of linear structure
(in a sense broader than ours)
and studied its implication on
the security of encryption algorithms [
The dimension of the sub-space is called
the linearity dimension of f.
We note that it was Evertse
who first introduced the notion of linear structure
(in a sense broader than ours)
and studied its implication on
the security of encryption algorithms [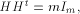
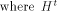 is the transpose of H
and
is the transpose of H
and 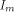 is the identity matrix of order m.
A Sylvester-Hadamard matrix of order
is the identity matrix of order m.
A Sylvester-Hadamard matrix of order 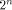 , denoted by
, denoted by 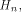 is generated by the following recursive relation
is generated by the following recursive relation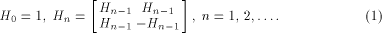
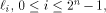 be the i row of
be the i row of 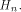 By Lemma 2 of [
By Lemma 2 of [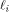 is the sequence of a linear function
is the sequence of a linear function 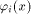 defined by the scalar product
defined by the scalar product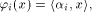 where
where 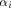 is the ith vector in
is the ith vector in 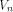 according to the ascending order.
according to the ascending order.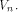 The Walsh-Hadamard transform
of f is defined as
The Walsh-Hadamard transform
of f is defined as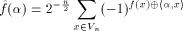
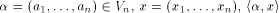 is the scalar product of
is the scalar product of 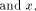 namely
namely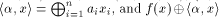 ,
is regarded as a real-valued function.
,
is regarded as a real-valued function.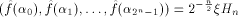
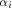 is the ith vector in
is the ith vector in 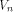 according to the ascending order
according to the ascending order 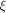 ,
is the sequence of f
and
,
is the sequence of f
and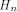 is the Sylvester-Hadamard matrix of order
is the Sylvester-Hadamard matrix of order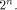
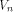 is called a bent function if
its Walsh-Hadamard transform satisfies
is called a bent function if
its Walsh-Hadamard transform satisfies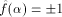
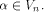
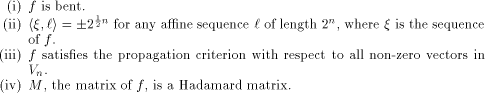
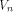 exist only when n is even [
exist only when n is even [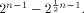
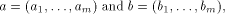 their component-wise product is defined by
their component-wise product is defined by 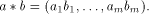 Let f be a function on
Let f be a function on 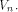 For a vector
For a vector 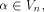 denote by
denote by 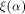 the sequence of
the sequence of 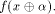 Thus
Thus 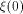 is the sequence of f itself
and
is the sequence of f itself
and 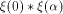 is the sequence of
is the sequence of 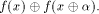
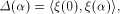
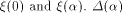 is also called
the auto-correlation of f with a shift
is also called
the auto-correlation of f with a shift  .
Obviously,
.
Obviously, 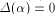 if and only if
if and only if 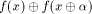 is balanced,
i.e., f satisfies the propagation criterion with respect to
is balanced,
i.e., f satisfies the propagation criterion with respect to 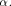 On the other hand, if
On the other hand, if 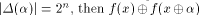 is a constant
and hence
is a constant
and hence  is a linear structure of f.
is a linear structure of f.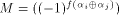 be the matrix of f and
be the matrix of f and 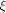 be the sequence of f.
Due to a very pretty result by R. L. McFarland
(cf. Theorem 3.3 of [
be the sequence of f.
Due to a very pretty result by R. L. McFarland
(cf. Theorem 3.3 of [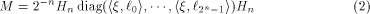
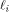 is the ith row of
is the ith row of 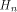 , a Sylvester-Hadamard matrix of order
, a Sylvester-Hadamard matrix of order 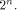
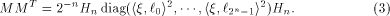
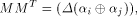
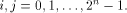
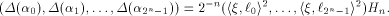
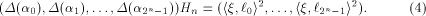
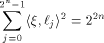
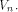
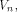 its rank coincides with its dimension.
its rank coincides with its dimension.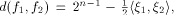 where
where 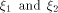 are the sequences of
are the sequences of 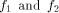 respectively.
(For a proof see for instance Lemma 6 of [
respectively.
(For a proof see for instance Lemma 6 of [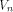 can be calculated by
can be calculated by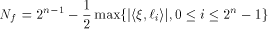
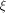 is the sequence of f and
is the sequence of f and
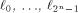 are the rows of
are the rows of 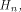 namely, the sequences of the linear functions on
namely, the sequences of the linear functions on 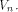
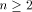 be a positive integer and
be a positive integer and 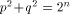 where both
where both
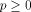 and
and 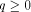 are integers. Then
are integers. Then 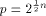
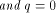 when n is even, and
when n is even, and 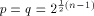 when n is odd.
when n is odd.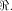
 Assume that f satisfies the propagation criterion with respect
to all but a subset
Assume that f satisfies the propagation criterion with respect
to all but a subset 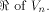 Note that
Note that 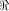 always contains the zero vector 0.
Write
always contains the zero vector 0.
Write 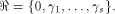 Thus
Thus 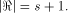
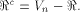 Then f satisfies the propagation criterion with
respect to all vectors in
Then f satisfies the propagation criterion with
respect to all vectors in 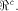
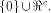 Then
Then 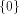 is a linear sub-space contained in
is a linear sub-space contained in 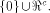 When
When 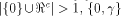 is a linear sub-space
for any nonzero vector in
is a linear sub-space
for any nonzero vector in 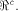 We are particularly interested in linear sub-spaces
with the maximum dimension contained in
We are particularly interested in linear sub-spaces
with the maximum dimension contained in 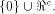 For convenience, denote by
For convenience, denote by  the maximum dimension
and by W a linear sub-space in
the maximum dimension
and by W a linear sub-space in 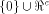 that achieves the maximum dimension.
that achieves the maximum dimension.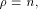 and f does not satisfy the propagation criterion with
respect to any vector if and only if
and f does not satisfy the propagation criterion with
respect to any vector if and only if 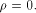 The case when
The case when 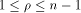 is especially interesting.
is especially interesting.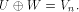 Then each vector
Then each vector 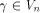 can be
uniquely expressed as
can be
uniquely expressed as 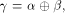 where
where 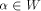 and
and 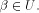 As the dimension of W is
As the dimension of W is 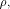 the dimension of U is equal to
the dimension of U is equal to 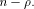 Write
Write 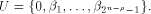
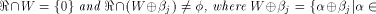
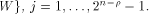
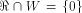 follows from the fact that
W is a sub-space of
follows from the fact that
W is a sub-space of 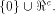 Next we consider
Next we consider 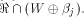
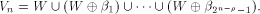
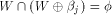
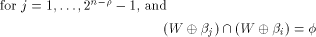
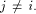 Assume for contradiction that
Assume for contradiction that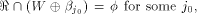
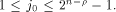 Then we have
Then we have 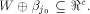 In this case
In this case 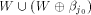 must form a sub-space of
must form a sub-space of 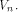 This contradicts the definition that
W is a linear sub-space with the maximum dimension in
This contradicts the definition that
W is a linear sub-space with the maximum dimension in 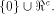 This completes the proof.
This completes the proof. satisfies
satisfies
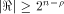 and
hence the rank of
and
hence the rank of 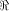 is at least
is at least 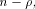 where
where  is the maximum dimension
a linear sub-space in
is the maximum dimension
a linear sub-space in 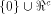 can achieve.
can achieve.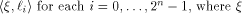 is the sequence of f and
is the sequence of f and
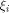 is a row of
is a row of 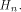
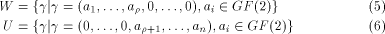
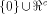 that achieves the maximum dimension
that achieves the maximum dimension  and
U is a complementary sub-space of W.
The more general case where
(5) or (6) is not satisfied
can be dealt with after employing
a nonsingular transform on the input of f.
This will be discussed in the later part of this section.
and
U is a complementary sub-space of W.
The more general case where
(5) or (6) is not satisfied
can be dealt with after employing
a nonsingular transform on the input of f.
This will be discussed in the later part of this section.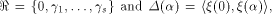 where
where 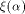 is the sequence of
is the sequence of 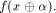 Since
Since 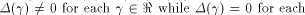
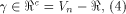 is specialized as
is specialized as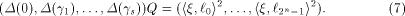
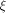 is the sequence of f,
is the sequence of f,
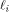 is the ith row of
is the ith row of 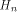 and Q comprises the 0th,
and Q comprises the 0th, 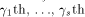 rows of
rows of 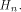 Note that Q is an
Note that Q is an 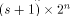 matrix.
matrix.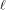 be the
be the 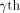 row of
row of 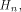 where
where 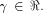 Note that
Note that  can be uniquely expressed as
can be uniquely expressed as 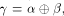 where
where 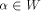 and
and 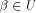 .
Let
.
Let 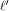 be the
be the 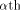 row of
row of 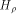 and
and
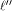 be the
be the 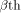 row of
row of 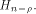 As
As
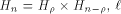 can be represented by
can be represented by 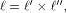 where
where  denotes the Kronecker product.
denotes the Kronecker product.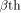 row of
row of 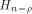 is an all-one sequence of length
if
and a balanced (1,-1)-sequence of length
is an all-one sequence of length
if
and a balanced (1,-1)-sequence of length 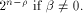
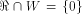 (see also Proposition 8).
There are two cases associated with
(see also Proposition 8).
There are two cases associated with 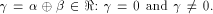 In the first case,
In the first case, 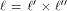 is the all-one sequence of length
is the all-one sequence of length 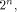 while in the second case,
we have
while in the second case,
we have 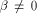 which implies that
which implies that
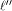 is a balanced (1,-1)-sequence of length
is a balanced (1,-1)-sequence of length 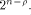 and hence
and hence 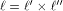 is a concatenation of
is a concatenation of 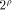 balanced (1,-1)-sequences of length
balanced (1,-1)-sequences of length 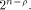
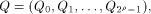 where each
where each 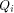 is a (1,-1)-matrix of
order
is a (1,-1)-matrix of
order 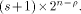 It is important to note that
the top row of each
It is important to note that
the top row of each 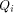 is
the all-one sequence,
while the rest are
balanced (1,-1)-sequences of length
is
the all-one sequence,
while the rest are
balanced (1,-1)-sequences of length 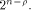
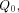 we have
we have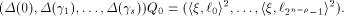
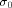 be the all-one sequence of length
be the all-one sequence of length 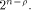 Then
Then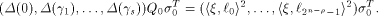
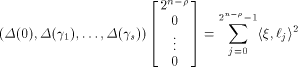
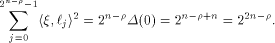
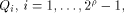 we have
we have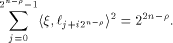
 satisfies the propagation criterion with respect
to all but a subset
satisfies the propagation criterion with respect
to all but a subset 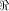 of vectors in
of vectors in 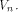 Set
Set 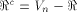 and let W be a linear sub-space with the maximum dimension
and let W be a linear sub-space with the maximum dimension 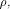 in
in 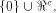 and U be a complementary sub-space of W.
Assume that W and U satisfy (5) and (6)
respectively.
Then
and U be a complementary sub-space of W.
Assume that W and U satisfy (5) and (6)
respectively.
Then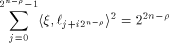
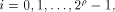 where
where
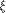 is the sequence of f and
each
is the sequence of f and
each 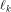 is a row of
is a row of 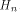
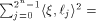
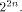 It implies that
It implies that 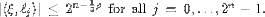 Therefore by Lemma 6 we have
Therefore by Lemma 6 we have 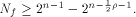
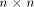 matrix A whose entries are from GF(2)
such that
the sub-spaces W' and U' associated with
f'(x) = f(x A) have the required forms.
f' and f have the same algebraic degree
and nonlinearity (see Lemma 10 of [
matrix A whose entries are from GF(2)
such that
the sub-spaces W' and U' associated with
f'(x) = f(x A) have the required forms.
f' and f have the same algebraic degree
and nonlinearity (see Lemma 10 of [ the nonlinearity of f
satisfies
the nonlinearity of f
satisfies 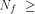
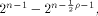 where
where  is the maximum dimension of the linear
sub-spaces in
is the maximum dimension of the linear
sub-spaces in 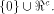
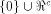 can achieve,
but not by the size of
can achieve,
but not by the size of 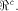
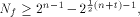 where t is the rank of
where t is the rank of 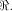 By Corollary 9, we have
By Corollary 9, we have 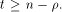 This implies that
This implies that 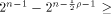
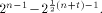 Thus Theorem 11
is an improvement to the result in [
Thus Theorem 11
is an improvement to the result in [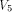
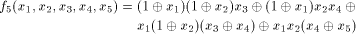
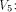
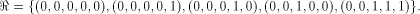
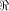 is equal to 3.
By using the result of [
is equal to 3.
By using the result of [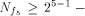
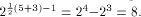 On the other hand,
we can set
On the other hand,
we can set 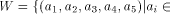
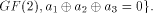 W is a four-dimensional sub-space in
W is a four-dimensional sub-space in 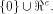
 =4, we have
=4, we have 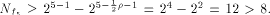 (Note that according to [
(Note that according to [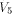 can achieve is 12.
Hence we have
can achieve is 12.
Hence we have 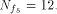 )
)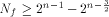 if f, a function on
if f, a function on 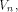 satisfies the propagation criterion
with respect to at least one vector in
satisfies the propagation criterion
with respect to at least one vector in 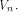 This section shows that this lower bound can be significantly improved.
Indeed we prove that
This section shows that this lower bound can be significantly improved.
Indeed we prove that 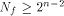 and also show that it is tight.
and also show that it is tight.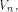 satisfies the propagation criterion with respect to
one or more vectors in
satisfies the propagation criterion with respect to
one or more vectors in 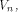 then the nonlinearity of f satisfies
then the nonlinearity of f satisfies 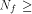
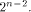
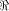 the set of vectors in
the set of vectors in 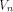 with respect to which the propagation criterion
is not satisfied by f.
We also let
with respect to which the propagation criterion
is not satisfied by f.
We also let 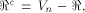 and W be a linear sub-space
in
and W be a linear sub-space
in 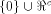 that achieves the maximum dimension
that achieves the maximum dimension 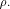
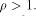 Next we consider the case when
Next we consider the case when 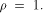 We prove this part by further refining
the Parseval's equation.
We prove this part by further refining
the Parseval's equation.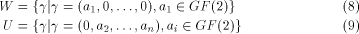
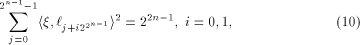
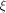 is the sequence of f and
is the sequence of f and 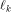 is a row of
is a row of 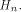
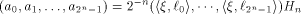

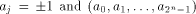 is the first row of the matrix M described in (2).
is the first row of the matrix M described in (2).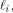 the ith row of
the ith row of 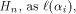 where
where 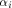 is the binary representation of an integer i
in the ascending alphabetical order.
Set
is the binary representation of an integer i
in the ascending alphabetical order.
Set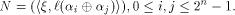
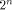 with integer entries.
In [
with integer entries.
In [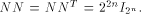 We can split N into four sub-matrices of equal size,
namely
We can split N into four sub-matrices of equal size,
namely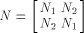
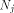 is a matrix of order
is a matrix of order 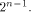 As
As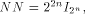 we have
we have 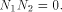
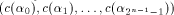 be an
arbitrary linear sequence of length
be an
arbitrary linear sequence of length 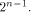
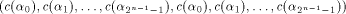
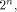 and hence a row of
and hence a row of 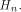 Thus from (11), we have
Thus from (11), we have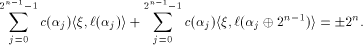
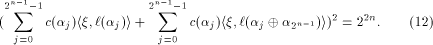
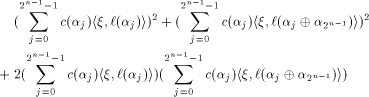
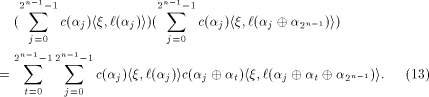
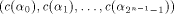 is a linear sequence,
is a linear sequence, 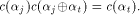
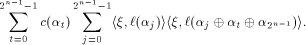
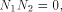
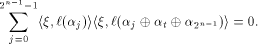
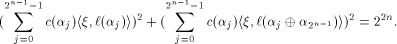
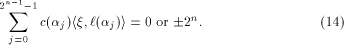
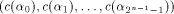 is an arbitrary
linear sequence of length
is an arbitrary
linear sequence of length 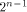 and each linear sequence of length
and each linear sequence of length 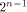 is a column of
is a column of 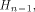 from (14) we have
from (14) we have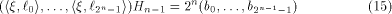
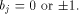 Therefore
Therefore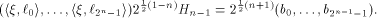
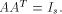 It is easy to verify that
It is easy to verify that 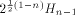 is an orthogonal matrix. Thus
is an orthogonal matrix. Thus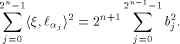
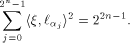
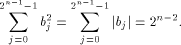
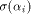 denote the ith row of
denote the ith row of 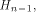 where
where 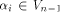 is the binary representation of
is the binary representation of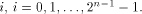 From (15),
From (15),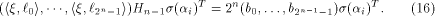
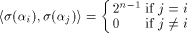

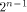 is on the ith position of the column vector.
is on the ith position of the column vector.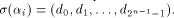 Then
Then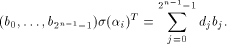
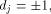 we have
we have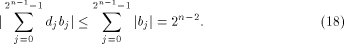
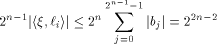
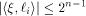
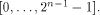 Similarly,
Similarly,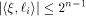
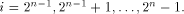 By Lemma 6, the nonlinearity of f satisfies
By Lemma 6, the nonlinearity of f satisfies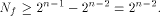
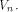 Then the following statements hold:
Then the following statements hold: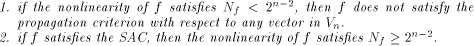
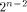 is tight.
We achieve the goal
by demonstrating a function on
is tight.
We achieve the goal
by demonstrating a function on 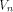 whose nonlinearity
is equal to
whose nonlinearity
is equal to 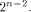 Let
Let 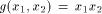 be
a function on
be
a function on 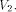 Then the nonlinearity of g is
Then the nonlinearity of g is 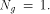 Now let
Now let
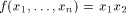 be
a function on
be
a function on 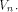 Then the nonlinearity of f is
Then the nonlinearity of f is 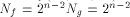 (see for instance Lemma 8 of [
(see for instance Lemma 8 of [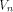 whose first two bits are nonzero,
which count for three quarters of the vectors in
whose first two bits are nonzero,
which count for three quarters of the vectors in 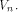 It is not hard to verify that
It is not hard to verify that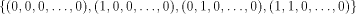
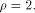 Thus we have a result described as follows:
Thus we have a result described as follows: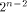 as stated in Theorem 12 is tight.
as stated in Theorem 12 is tight.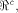 the set of vectors where the propagation criterion
is satisfied by a function on
the set of vectors where the propagation criterion
is satisfied by a function on 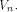 For all the functions we know of,
For all the functions we know of,
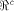 is either an empty set
or a set with at least
is either an empty set
or a set with at least 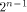 vectors.
We believe that
any further understanding of this problem
will contribute to
the research into
the design and analysis of
cryptographically strong
nonlinear functions.
vectors.
We believe that
any further understanding of this problem
will contribute to
the research into
the design and analysis of
cryptographically strong
nonlinear functions.