| Submission Procedure |
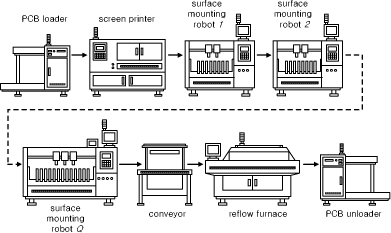
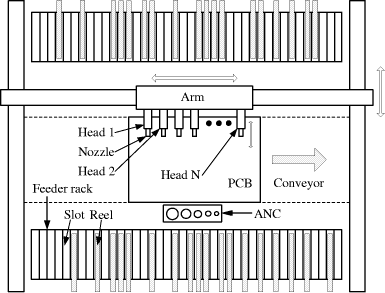
An Efficient Planning Algorithm for Multi-head Surface Mounting Machines using a Genetic AlgorithmWonsik Lee Sunghan Lee Beomhee Lee Youngdae Lee Abstract: In this paper, a genetic algorithm based method is proposed to solve the problem of minimizing the PCB assembly time for multi-head surface mounting machines. By grouping the reels and by clustering the components the multi-head problem is transformed into a single-head one and then the single-head method is simply applied to the multi-head case. To implement the genetic algorithm, a partial link concept is proposed for genetic operations. Computer simulation results show that the proposed algorithm is superior to the heuristic algorithm that is currently used in industry. Key Words: Genetic algorithm, PCB assembly time, multi-head surface mounting machine 1 IntroductionPrinted circuit boards (PCBs) are the brains of electronic products. PCB assembly is an important sector of the electronics manufacturing industry [Maimon et al. 93]. With recent developments in component manufacturing technology, surface mounting technology has replaced the pin-through-hole technology and has made it easier to mount components on a PCB automatically. Efficient operations in PCB assembly are essential for reducing production costs and thereby increasing competitiveness. There has been an increasing research interest in optimal PCB assembly planning. The overall PCB assembly time depends on two decision variables: i) the assignment of reels to slots on feeder racks; and ii) sequencing of pick-and-place movements [Ball and Magazine 88]. These two problems are combinatorial optimization problems, which are known to be NP-hard [Laarhoven and Zijm 93]. Although these problems are highly interrelated, it is difficult to solve these problems concurrently. Therefore, during the last decade, most research on minimizing the PCB assembly time solved these problems by decoupling one from the other [Lee et al. 99]. Page 833 [Ball and Magazine 88] used heuristic to separate the problem into two decoupled problems and solved them individually. [Leipälä and Nevalainen 89] formulated component pick-and-place sequencing as a 3-dimensional asymmetric traveling salesman problem (TSP) and reel assignment as a quadratic assignment problem. They obtained suboptima with a modified farthest insertion heuristic. [Bard et al. 94] modeled reel assignment as a quadratic integer program and component pick-and-place sequencing as a TSP. They developed heuristic methods based on a weighted nearest neighbor TSP technique and a Lagrangian relaxation scheme. [Kumar and Li 95] formulated reel assignment as a minimum weight matching problem and component pick-and-place sequencing as a TSP. All these algorithms limited the total number of heads on the surface mounting machine to at most three to reduce the complexity of the problems. While the travel time is the most significant factor in minimizing the PCB assembly time when the number of heads is small, the pick time becomes a more significant factor as the number of heads increases. The reason is that one simultaneous pickup of multiple components can reduce a large portion of the assembly time for the multi-head surface mounting machine. In this paper, we propose a new genetic algorithm (GA) based approach for a multi-head surface mounting machine. The results indicate that the proposed method results in about 10.7% average saving in PCB assembly time compared with the heuristic algorithm which is commonly used in industrial settings. The organization of this paper is as follows: [Section 2] is a description of the multi-head surface mounting machine. In [Section 3], a partial-link GA method is proposed for the singlehead surface mounting machine. [Section 4] presents the technique for solving the multi-head case by modifying the single-head case. In [Section 5], the improvement in efficiency and efficacy of the proposed algorithm compared to the heuristic algorithm (HA) in current use is verified through computer simulation. [Section 6] concludes this paper. 2 Problem statement[Fig. 1] shows a PCB assembly line which assembles surface mounted devices. The line consists of a PCB loader, a screen printer, a series of surface mounting machines (SMM), a conveyor, a reflow furnace and a PCB unloader. PCBs are transferred from the PCB loader to the PCB unloader by the conveyor. The screen printer prints solder paste on the PCBs and then the surface mounting machines mount components on them. Finally, the reflow furnace heats PCBs so that the components are fixed on the PCBs. Most of the total assembly time is the pick-and-place time at the surface mounting machines [Bard et al. 94]. Therefore, varieties of surface mounting machines have been developed to minimize the pick-and-place time mechanically. Recently, the multi-head surface mounting machine is becoming increasingly popular because it can obtain high mounting speed with relatively low cost. This paper considers this type of machine. [Fig. 2] shows a schematic diagram of a multi-head surface mounting machine.
Page 834 Figure 1: PCB assembly line for surface mounted devices.
The PCB assembly time on the multi-head surface mounting machine is dependent on two decision problems. First, a reel assignment problem determines which reel is to be assigned to which slot on the feeder racks. Next, a sequencing problem determines the sequence of pick-and-place movements of the arm, assuming that each reel's position on the racks is fixed by the solution of the reel assignment problem. As mentioned in [Section 1], these problems are NP-hard. Until recently, algorithm designers have been trying to solve the reel assignment and the sequencing problems by decoupling one from the other to simplify matters. However, since the reel assignment and the sequencing are highly interrelated, they should be solved concurrently. In this paper, we propose a partial-link GA method for jointly solving the reel assignment and the sequencing. Page 835 Figure 2: Schematic diagram of a multi-head surface mounting machine. In order to solve this problem, we will first consider the single-head case and then apply the single-head method to the multi-head case. The PCB assembly time can be thought to be composed of four factors: the travel time, the nozzle change time, the pick time and the place time. In the single-head case, the pick time and the place time are constant. Hence, we will try to minimize the travel time and the nozzle change time in the single-head case, which is described in detail in [Section 3]. This approach is, however, not directly applicable to the multi-head case. With a large number of heads, each simultaneous pickup operation saves a large amount of time. For example, when the arm picks up five components simultaneously, the time needed to pick up four components sequentially can be saved. This means that we can also reduce the pick time. In fact, in the multi-head case the pick time is the most significant factor in minimizing the PCB assembly time. Therefore, we will try to maximize the number of simultaneous pickups in the multi-head case. We call a group of reels that is used for simultaneous pickup a reelgroup. Once all the reel-groups are constructed, the remaining problems can be modeled as a single-head problem by thinking of each reel-group as one reel. The algorithm for the multi-head case is described in [Section 4]. The assumptions made in solving the problem are as follows:
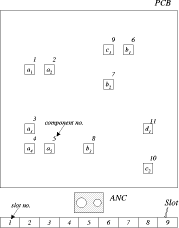
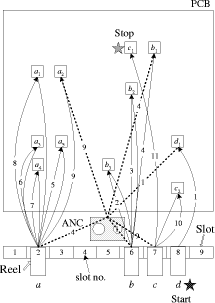
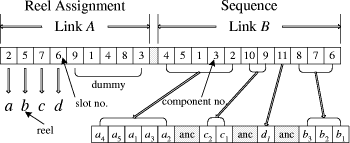
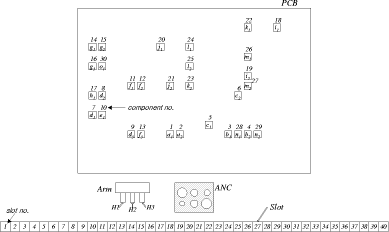
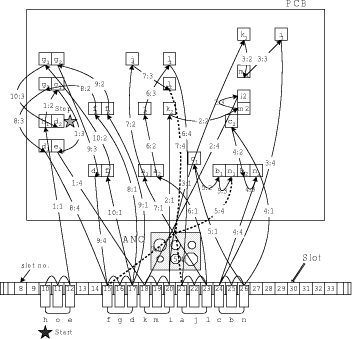
Page 836 The following notations are used in this paper: 3 Single-head SMMIn this section, we try to minimize the entire assembly time of the single-head surface mounting machine. First, we describe the genetic algorithm and solve the reel assignment and the sequencing problems by decoupling one from the other using GA method. Then, we propose partial-link GA method for jointly solving the reel assignment and the sequencing in the single-head case. A sample PCB with 11 components in 4 different component types is used as an example in solving the single-head case. [Tab. 1] gives the information about the nozzle and the number of components for each component type. The surface mounting machine has a single head and 9 slots. [Fig. 3] shows the locations of the components, slots and ANC. A serial number is given to each slot and each component.
Table 1: Single-head case: nozzle and number of components for each component type 3.1 Solving with GA3.1.1 GA overviewGenetic Algorithms (GAs), as one of the adaptive algorithms, have been high-lighted in a variety of fields and successfully applied to many engineering problems [Grefenstette et al. 85, Whitley et al. 89, Wong and Leu 93, Murata et al. 96, Lee and Lee 97, Dasgupta and Michalewicz 97]. Page 837 Figure 3: Single-head case: locations of the components, slots and ANC GA is different from conventional optimization methods in several ways. It is a sort of population oriented search technique that uses probabilistic transition rules to evolve multiple potentials. It is a parallel and global search method that can find the global solution utilizing multiple candidate solutions. GA is mainly composed of three basic operators: reproduction; crossover; and mutation [Goldberg 89, Davis 91, Michalewicz 96]. 3.1.2 Reel assignment problemThe reel assignment problem is determining the assignment of types of
components to slots. In the genetic algorithm, the reel assignment is designated
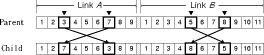
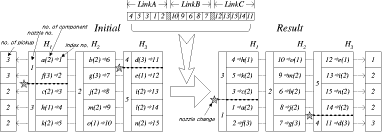
by link. The link is defined as Figure 4: Single-head case: a feasible link for reel assignment The first gene indicates that the first component type is assigned to slot 5, the second gene indicates that the second component type is assigned to slot 7, and Page 838 so on. The right part of [Fig. 4] shows the assignment of reels to slots. Hence, it can be easily seen that the five genes at the tail do not have any effect on the reel assignment. This is the reason why they are called dummy genes. The fitness function, which is the total distance, means the sum of the distances between each component and its respective reel. Then the fitness function can be defined as follows:
3.1.3 Sequencing problemThe sequencing problem is determining the sequence of pick-and-place
movements at each machine, assuming that reels of components are assigned
and fixed to slots on the feeder racks. In the genetic algorithm, the reel
assignment is designated by link. The link is defined as
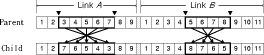
Figure 5: Single-head case: a feasible link for sequence The number in each gene represents the component number. The first gene indicates that the machine mounts component 3 first, the second gene indicates that the machine mounts component 7 second, and so on. We now define the fitness function which represents the efficiency of solutions. The fitness function is defined as the total assembly time. Before the assembly task starts, the head is equipped with an appropriate nozzle and is positioned over the starting reel. The overall path starts at the first reel and ends at the last mounting position. The nozzle may be changed while the head moves from a mounting position to the next reel. Then the fitness function can be defined as follows: where
The first term in [Eq. 2], above, represents the moving time from the reel to the mounting position and the second term represents the moving time from the Page 839 mounting position to the reel. The second term includes the nozzle change time if needed. The resulting reel assignment and sequence are illustrated in [Fig. 6]. It can be seen that each reel has been assigned to the reasonable position near the mounting positions. The total assembly time is 7.55 sec which is reduced by 3.7 percent compared with HA(7.84 sec) .
Figure 6: Single-head case: reel assignment and sequence by genetic algorithm 3.2 Solving with partial-link GAA link for jointly solving the reel assignment and the sequencing consists of two partial links: one for the reel assignment and the other for the sequencing. The first link is named A and the second one B. Using our partial-link GA method, we combine link A and link B, thus we can construct a new link for jointly solving the reel assignment and the sequencing. The fitness function is defined as the total assembly time (see [Eq. 2]). The main features of the SMM planning algorithm based on GA search in this paper can be described as follows:
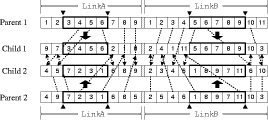
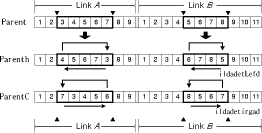
Page 840 3.2.1 Partial-link operators[Fig. 7] shows the partial-link crossover operator. We pick certain bit positions of parent 1 (or 2) and place them at the same position in the child. Then we fill the remaining positions by the missing entries in the same order as these entries occur in parent 2 (or 1).
Figure 7: Partial-link crossover operator The exchange operator, inversion operator and rotation operator are used as a mutation operator. The exchange operator exchanges two genes in a parent link. [Fig. 8] shows the partial-link exchange operator. The inversion operator takes a segment from a parent link and flips it to form a new link. [Fig. 9] shows the partial-link inversion operator. The rotation operator rotates a segment of a parent link to the right or left to create a new link. [Fig. 10] shows the partial-link rotation operator. 3.2.2 Parameter controlThe issue of controlling values of various parameters of an evolutionary algorithm is one of the most important and promising areas of research in evolutionary computation. [Eiben, A. et al. 99] distinguish two major forms of setting parameter values: parameter tuning and parameter control. The parameter tuning is the approach that finds good parameter values, which remain fixed during the run of the algorithm. The parameter control related to crossover and mutation are not fixed but varied depending on the fitness value of the solutions. It enhances the search performance and avoids premature convergence. It has been observed that the difference between the maximum and average fitness value of the population is likely to be less for a population that has converged to the optimum solution than that for a population scattered in the solution space [Srinivas and Patnaik 94]. To achieve a smooth convergence of the population of solutions, it is required that the high fit chromosomes undergo less perturbation than the low fit chromosomes. Regarding this fact, we modify the crossover and mutation probability as follows: Page 841 Figure 8: Partial-link exchange operator Figure 9: Partial-link inversion operator Figure 10: Partial-link rotation operator where 3.2.3 Application of partial-link GAThe overall procedure for our partial-link GA for single-head SMM can be denoted as follows. Step 1: Assign the parameters of SMM and GA. Page 842 Step 5: Calculate the fitness and control GA parameters. The above procedure is applied to the sample PCB. [Fig. 11] shows the total assembly time (the fitness value) versus the number of generations. The total assembly time is reduced by 11.3 % from the best initial guess in 24 generations. The total assembly time is 7.40 sec which is reduced by 5.6 percent compared with HA(7.84 sec). The link obtained at the 24th generation is shown in [Fig. 12] and the corresponding reel assignment and sequencing are illustrated in [Fig. 13]. It can be seen that each reel has been assigned to the reasonable position near the mounting positions. It can also be seen that the number of nozzle changes, which are the most time-consuming operations, is minimized. The most important thing that should be noticed here is that reels are assigned near to the ANC, resulting in timesavings. This is because the partial-link GA method can consider ANC by solving the problems of reel assignment and sequencing concurrently. Figure 11: Single-head case: reel assignment and sequencing resulted by the partial-link genetic algorithm 4 Multi-head SMMIn this section, we try to minimize the entire assembly time of the multi-head surface mounting machine by using our partial-link GA method. Considering the characteristics of the multi-head case, we focus on minimizing the pick time. We Page 843 Figure 12: Single-head case: reel assignment and sequence achieved at the 24th generation Figure 13: Single-head case: reel assignment and sequencing resulted by the partial-link genetic algorithm construct reel-groups so that the number of simultaneous pickups is maximized. The problem is decomposed into four phases: assignment of reels to heads; construction of reel-groups; construction of component clusters; and application of the partial-link GA method. A sample PCB with 30 components in 15 different component types is used as an example in jointly solving the reel assignment and the sequencing in the multi-head case. [Tab. 2] gives the information about the nozzle and the number of components for each component type. The surface mounting machine has 3 heads and 40 slots. [Fig. 14] shows the locations of the components, slots and ANC. Page 844
Table 2: Multi-head case: Nozzle and the number of components for each component type Figure 14: Multi-head case: locations of the components, slots and ANC 4.1 Assignment of reels to headsWe must determine which head is used for each reel before constructing reel-groups. The way to assign the reels to the heads is guided by the following two conditions:
In order to minimize the number of nozzle changes, we assign the reels that use the same nozzle to the same head. We define five sets of reels as follows, each of which uses the same nozzle.
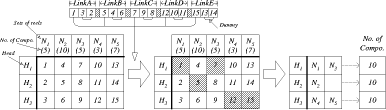
We now assign these sets to the heads in such a way that each head has the same amount of workload. This problem can be modeled as follows; we choose only one element in each column of the 3 x 5 matrix, which is shown in the left part of [Fig. 15]. To apply the GA, we number all the elements in the matrix. The link consisting of five partial-links can be defined as follows: Page 845 Figure 15: Partial-link GA assignment of reels to heads
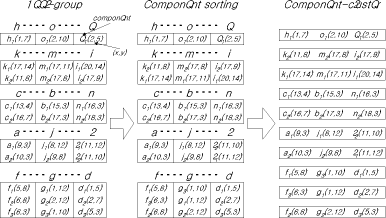
The first gene in each link represents the selected element in each column. Hence, the remaining two genes are dummy. The fitness function is defined as a deviation among the numbers of components which are assigned to each head. The GA has found that the optimal link is [1,3,2|5,4,6|7,9,8|12,10,11|15,13,14]. The corresponding assignment is shown in the middle part of [Fig. 15]. It can be seen that each head has exactly the same workload. 4.2 Construction of reel-groupsFor reel-group construction, we define the fitness function as the sum of the pick time and the nozzle change time. A simple method to construct reel-groups is as follows; the first reel-group is constructed by taking the first reel from each of the three heads, the second reel-group by taking the second reel from each head, etc. The resulting reel-groups are {a,b,d}, {f,g,e}, {c,j,i}, {h,m,l} and {k,o,n}, and are shown in the left part of [Fig. 16]. Figure 16: Partial-link GA construction of reel-groups Since the same group of nozzles is used for {c,j,i}, {h,m,l} and {k,o,n}, only three groups of nozzles are needed. Consequently, the assembly task can be Page 846 completed by two nozzle changes. Therefore, the fitness value can be calculated as (3+3+2+2+2) x Tpick + 2 x Tanc. Now we try to minimize the fitness function using the GA. The link consisting of three partial-links can be defined as follows:
The GA has found that the optimal link is [4,5,3,1,2|10,9,6,8,7|12,13,15,14,11]. The resulting reel-groups are shown in the right part of [Fig. 16]. Its fitness value is (1+2+2+2+3) x Tpick + 2 x Tanc. It can be seen that the time needed to pick up two components separately was saved compared with the initial solution. 4.3 Construction of component-clustersWhile mounting a PCB, a cycle consists of the pick-and-place movements. During the first phase of a cycle, the heads pick up components from reels simultaneously. During the next phase of a cycle, the arm moves to the board and places the components sequentially. The nozzle at each head may be changed while the arm moves from the last mounting position in a cycle to the first pickup position in the next cycle. A set of components to be processed in each cycle is called a component-cluster. Component-clusters can be constructed as follows: Step 1: Sort the components of each reel in ascending order of
the x-coordinate and then sort those components with identical x-coordinates
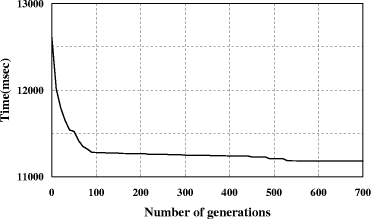
in ascending order of the y-coordinate; [Fig. 17] shows the process of component-cluster construction. Once all the component-clusters are constructed, it is not necessary to find out the mounting sequencing in each cycle. The reason is that the order in which the heads operate is predetermined, as described in [Section 2]. 4.4 Application of the partial-link methodA GA link for solving the multi-head case problem consists of four partial links: 1) the link for the assignment of reels to heads; 2) the link for the construction of reel-groups; 3) the link for the reel-group assignment; and 4) the link for the component-cluster sequencing. By combining these four links, we can produce the GA link for solving the multi-head problem. We use the partial-link operators on the sample PCB described above. [Fig. 18] shows the total assembly time (the fitness value) versus the number of generations. The total assembly time is reduced by 12.7 percent from the best initial guess in 553 generations. The resulting reel-group assignment and component-cluster sequencing are illustrated in [Fig. 19]. It can be seen that the reels in each reel-group have been assigned to reasonable positions such that they can be simultaneously reached by the heads. Page 847
Figure 17: Component-cluster construction It can also be seen that the assembly task is completed by two nozzle changes, which is minimal. Figure 18: Multi-head case: Total assembly time versus number of generations Page 848
Figure 19: Multi-head case: Reel-group assignment and component-cluster sequencing achieved at the 553rd generation 5 Simulation resultsWe have proposed a partial-link GA method for minimizing the PCB assembly time. To evaluate the proposed method, the total assembly time is compared with that of the heuristic algorithm which is currently used in industry. In industrial settings, a greedy assignment algorithm is commonly used for assigning reels, and the nearest neighbor rule is used for sequencing pick-and-place movements. The efficiency of the proposed method is tested on three types of real-life
surface mounting machines which are used in Yamaha settings. The only difference
among those types is the number of heads. The speed of the machine is 1.5
m/s. The pickup (or placement) time is 0.15 seconds and the nozzle change
time is 0.85 seconds. Since an exhaustive examination of the quality of
solutions requires a large number of problems, the algorithm is tested
on a set of randomly generated problems. A random number generation program
is used for generating uniformly distributed mounting position coordinates.
It is required that the x, y-coordinates of mounting positions satisfy
the constraint that 50 [Tab. 3] gives the results for 50 different problems. For each problem, the numbers of components and reels are given. It can be seen that the number of reels (or components) increases as the board identification number increases, which means that the problem gets more complex as the board identification number increases Page 849 which means that the problem gets more complex as the board identification number increases.
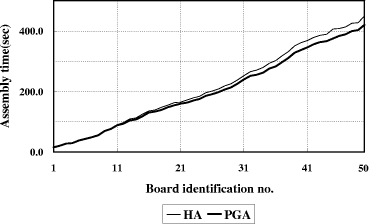
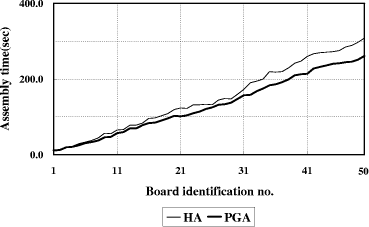
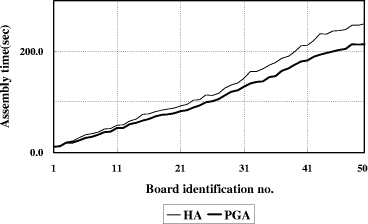
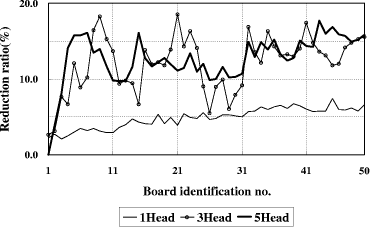
Table 3: Board characteristics. [Fig. 20] shows the results in the single-head case. The upper curve represents PCB assembly times by using the heuristic algorithm and the lower curve by the partial-link GA method. The difference between the two curves represents the time saved by the partial-link GA method over the heuristic algorithm. The results in the 3-head case and 5-head case are given in [Fig. 21 and 22]. Note that in all cases the saved time increases as the board identification number increases. This means that performance of the partial-link GA improves as the problem gets more complex. [Fig. 23] shows the PCB assembly time improvement by the partial-link GA over the heuristic algorithm. The result indicates that all over the range of tested boards the proposed algorithm results in 5.3% average savings in total assembly time in the single head case, 13.1% in the 3-head case, and 13.7% in the 5-head case, respectively, compared to the heuristic algorithm. It shows Page 850 Figure 20: Simulation results in the single-head case Figure 21: Simulation results in the 3-head case that performance improves as the number of heads increases, which means the proposed method performs well on the multi-head surface mounting machine. It also shows that the partial-link GA performs better than the heuristic algorithm as the number of reels and components increases. Page 851
Figure 23: PCB assembly time improvement by the partial-link GA over HA. Page 852 6 ConclusionIn this paper, we proposed a partial-link GA method to solve the problem of minimizing the PCB assembly time for multi-head surface mounting machines. The merits of the proposed GA method can be summarized in the following statements.
As a result, the proposed algorithm is expected to improve the PCB mounting productivity and enable the construction of a more competitive assembly line. References[Ball and Magazine 88] Ball, M. O., Magazine, M. J.: "Sequencing of insertions in printed circuit board assembly"; Operations Research, 36,2(1988), 192-201. [Bard et al. 94] Bard, J. F., Clayton, R. W., Feo, T. A: "Machine setup and component placement in printed circuit board assembly"; International Journal of Flexible Manufacturing Systems, 6,1 (94), 5-31. [Davis 91] Davis, L.: "Handbook of Genetic Algorithms"; Van Nostrand (1991). [Dasgupta and Michalewicz 97 ] Dasgupta, D., Michalewicz, Z.: "Evolutionary Algorithms in Engineering Applications"; Springer Verlag (1997). [Eiben, A. et al. 99] Eiben, A. E., Hinterding, R., Michalewicz, Z.: "Parameter Control in Evolutionary Algorithms"; IEEE Trans. on Evolutionary Computation, 2, 3 (1999), 124-141. [Goldberg 89] Goldberg, D.E.: "Genetic Algorithms in Search, Optimization, and Machine learning"; Addison Wesley (1989). [Grefenstette et al. 85] Grefenstette, J. J., Gopal, R., Rosmaitaa, R., Gucht, D. V.:"Genetic algorithm for the traveling salesman problem"; Proc. International Conference on Genetic Algorithms and Their Applications, (1985), 160-168. Page 853 [Kumar and Li 95] Kumar R., Li, H.: "Integer programming approach to printed circuit board assembly time optimization"; IEEE Trans. on Components, Packaging and Manufacturing Technology, Part B : Advanced Packaging, 18,4 (1995), 720-727. [Laarhoven and Zijm 93] Laarhoven P. V., Zijm, P. V.: "Production preparation and numerical control in PCB assembly"; International Journal of Flexible Manufacturing Systems, 5,3 (1993), 187-207. [Lee and Lee 97] Lee, Y. D., Lee, B. H.: "Genetic Trajectory Planner for a Manipulator with Acceleration Parameterization"; Journal of Universal Computer Science, 3,9 (1997), 1056-1073. [Lee et al. 99] Lee, S. H., Park, T. H., Lee, B. H.: "A hierarchical method to improve the productivity of multi-head surface mounting machines"; to appear in Intelligent Automation and Soft Computing. [Leipälä and Nevalainen 89] Leipälä, T., Nevalainen, O.: "Optimization of the movements of a component placement machine"; European Journal of Operational Research, 38,3 (1989), 167-177. [Maimon et al. 93] Maimon, O. Z., Dar-El, E. M., Carmon, T. F.: "Set-up saving schemes for printed circuit boards assembly"; European Journal of Operational Research, 70,2 (93), 77-190. [Michalewicz 96] Michalewicz, Z.: "Genetic Algorithms + Data Structures = Evolution Programs"; Springer-Verlag (1996). [Murata et al. 96] Murata, T., Ishibuchi, H., Tanaka, H.: "Genetic algorithms for flowshop scheduling problems"; Computers & Industrial Engineering, 30,4 (1996), 1061-1071. [Srinivas and Patnaik 94] Srinivas M., Patnaik L. M.: "Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms"; IEEE Trans. on System, Man and Cybernetics,24,4 (1994), 656-667. [Whitley et al. 89] Whitley, D., Starkweather, T., Fuquay, D.: "Scheduling problems and traveling salesmen: the genetic edge recombination operator"; Proc. International Conference on Genetic Algorithms and Their Applications, (1989), 133-140. [Wong and Leu 93] Wong, H., Leu, M. C.: "Adaptive genetic algorithm for optimal printed circuit board assembly planning"; Proc. Annals of the CIRP,42, 1 (1993), 17-20. Page 854 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
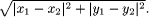 .
.

 C
C 
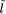 = [l(1), l(2), ..., l(m)] where l(i)
= [l(1), l(2), ..., l(m)] where l(i) 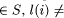 l(j) if
l(j) if 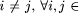 {1,2 ..., m}. Gene l(i) represents the slot where the component type i
is assigned. Actually the reel assignment is determined by only the first
p genes and thus the other m-p genes are dummy genes.
A feasible link is shown in the left part of [Fig. 4]. The number in each
gene represents the slot number.
{1,2 ..., m}. Gene l(i) represents the slot where the component type i
is assigned. Actually the reel assignment is determined by only the first
p genes and thus the other m-p genes are dummy genes.
A feasible link is shown in the left part of [Fig. 4]. The number in each
gene represents the slot number. 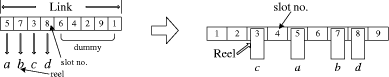
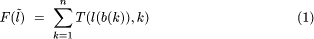
 l*(j) if i
l*(j) if i  j
j 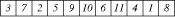
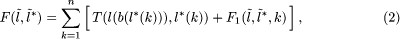
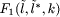
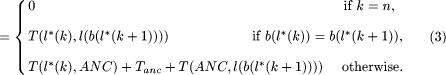
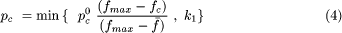
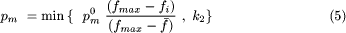
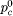 and
and 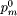 is the original crossover and mutation probability, respectively.
pc and pm are the modified probabilities,
respectively. fmax and
is the original crossover and mutation probability, respectively.
pc and pm are the modified probabilities,
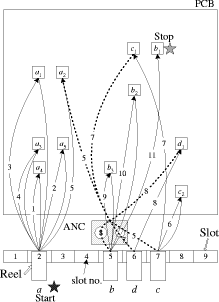
respectively. fmax and 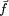 are maximum and average
fitness, respectively. k1 and k2, which
are the threshold values, have to be less than 1.0. They normalize pc
and pm to the range 0.0-1.0. fc is
the average fitness value of the two chromosomes selected for crossover
and fi is the fitness of the ith chromosome to
which the mutation with probability pm is applied.
are maximum and average
fitness, respectively. k1 and k2, which
are the threshold values, have to be less than 1.0. They normalize pc
and pm to the range 0.0-1.0. fc is
the average fitness value of the two chromosomes selected for crossover
and fi is the fitness of the ith chromosome to
which the mutation with probability pm is applied. 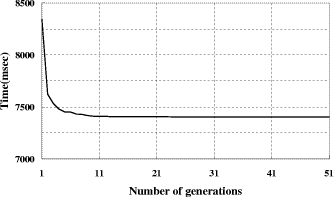


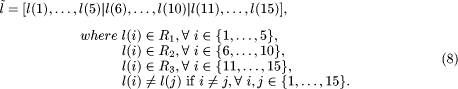
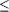 x
x