| Submission Procedure |
Transformational Approaches to the Specification and Verification of Fault-Tolerant Systems: Formal Background and ClassificationFelix C. Gärtner Abstract: Proving that a program suits its specification and thus can be called correct has been a research subject for many years resulting in a wide range of methods and formalisms. However, it is a common experience that even systems which have been proven correct can fail due to physical faults occurring in the system. As computer programs control an increasing part of todays critical infrastructure, the notion of correctness has been extended to fault tolerance, meaning correctness in the presence of a certain amount of faulty behavior of the environment. Formalisms to verify faulttolerant systems must model faults and faulty behavior in some form or another. Common ways to do this are based on a notion of transformation either at the program or the specification level. We survey the wide range of formal methods to verify faulttolerant systems which are based on some form of transformation. Our aim is to classify these methods, relate them to one another and, thus, structure the area. We hope that this might faciliate the involvement of researchers into this interesting field of computer science. Key Words: fault tolerance, specification, verification, transformation, fault model, failure model Category: C.4 (fault tolerance; modeling techniques), F.3.1 (mechanical verification; specification techniques) 1 IntroductionAs our daily life increasingly depends on the wellfunctioning of computer systems, a system failure due to a programming or design mistake can have catastrophic consequences. It is a wellknown fact in modern software engineering that software systems of a certain size almost definitely contain such errors; much design experience and programming discipline are necessary to minimize their number. A complementary approach which is sometimes taken is the use of formal methods in software development. With this approach it is possible to prove that some system is free of such errors. This results in a very strong notion of correctness. One drawback of this approach is that the system requirements must be formulated very precisely; in fact they must be formulated unambiguously in some mathematical formalism so that the question of whether or not a system suits its requirements can be reduced to the question whether or not an assertion is provable in some mathematical system [33]. The formal version of the system requirements is usually called a (formal) specification. The process of proving that a given program suits its formal specification is called verification. Even if computer systems are proved correct, they might fail in practice. This is mostly due to physical faults in the underlying hardware which cannot Page 668 be avoided. Critical systems must suit their specification even in the presence of such faults. Systems with this type of property are called fault tolerant. Methods to prove faulttolerant systems correct must necessarily explicitly or implicitly deal with faulty behavior. In this article, we are interested in such formal methods to verify faulttolerant systems. More specifically, we study those methods which are based on the notion of a transformation. A transformation is a very general concept. Usually it means
the change of appearance, form or character of something, especially in
a way that improves its properties. A program transformation for example
changes a given program P into a transformed program A system is usually defined as a ``thing'' that interacts with its environment in a discrete fashion across a welldefined boundary (called the interface) [33]. If such interaction takes place, then it is called an open system. If it does not interact with its environment, then it is called closed. It is usually helpful to think of a system as being built in a hierarchical manner, i.e. a system is composed of many subsystems [50]. Each subsystem (sometimes also called a component) can interact with the other subsystems and the original system interface through its own interface (see Fig. 1).
Figure 1: System, subsystem, interface and interaction. The use of transformations in fault tolerance usually builds on the view that a faulttolerant systems is composed of a basic, faultintolerant system together with a set of special faulttolerance components [53, 7]. As transformations are often understood as improving properties, adding such components to a system which improve on performance or robustness can be viewed as a system transformation. This can refer to hardware (e.g. adding more main memory or redundant processors), software (e.g. installing a new replication software) and thus also to system properties (e.g. robustness or processing speed). But because transformations also change the properties of an object, it is not surprising that the concept of a transformation has been adapted in formal Page 669 methods dealing with fault tolerance. As the occurrence of faults obstruct the normal execution of programs, the effects of a faulty environment can be modeled as a transformation at the program level. Equally, faults obviously change program properties, so the effects of faults can be modeled as a transformation of a specification. There is a wide range of research literature in faulttolerant computing which builds on these ideas. In this article we attempt to classify these methods and, by doing this, survey the area. The classification is based on the following three distinctive features:
The resulting eight classes are treated in Sect. 3 and Sect. 4. We start with transformations on the subsystem level (Sect. 3) followed by transformations on the system level (Sect. 4). We always treat program transformations first and then specification transformations. This organization might seem a little overwhelming at first sight, but we have chosen this form of presentation because, from our experience, it is best suited to incrementally present the multiple ideas of this area in a fashion that clearly separates the concerns involved. In Sect. 5 we will take up many of the seemingly loose ends of the beforementioned exposition and present the methodologies and proof techniques in a concise manner. Sect. 6 will summarize the main points touched in the course of the exposition, and Sect. 7 concludes this paper and sketches directions for future work. We assume the reader is an interested novice in the field and has some basic knowledge of logic and formal systems. This assumption allows us to present the formal preliminaries (e.g. the system model, definitions of terms) in a rather condensed manner in Sect. 2. If necessary, introductory texts on formal specification (like the ``interview'' of Lamport [33]) should be consulted prior to reading this article. However, as complementary reading, we suggest Rushby's wellwritten survey of critical system properties [57]. 2 Definition of TermsMany refined formalisms have been introduced to specify distributed systems. Instead of following such a particular formalism, we will try to argue at a semantic level on the basis of temporal logic [56, 33]. Briefly spoken, in temporal logic a program is viewed as a generator of behaviors. Arguing at a semantic level means that we will discuss the properties of programs on the basis of the generated state sequences rather than using a particular specification language to express them. 2.1 States and BehaviorsAssume there is a nonempty set of variables V = {v1...,vn }. Each variable vi can store a value from a fixed value domain Di . The set of all possible combinations of value assignments to variables is called the state space. A state is one Page 670 element from the state space. Consequently, a state predicate (which is usually expressed as a first order logical formula) is a set of states, i.e. a subset of the state space. A behavior (or execution) over V is an infinite
sequence Stuttering is an important concept to model program refinement. Informally
spoken, state transitions at a lower level of abstraction appear in high
level behaviors as stuttering steps. A behavior There are two main types of properties called safety and liveness.
Informally, a safety property states that some ``bad'' thing never happens.
Thus, a safety property rules out a set of unwanted behavior prefixes.
In general, if a property is finitely refutable, then it is a safety property.
Formally, a property P is a safety property iff (if and only
if), taken any behavior Liveness properties informally state that some ``good'' thing will eventually happen. Formally, a property P is a liveness property iff every finite sequence of states is a prefix of a behavior in P. In contrast to safety properties, a liveness property cannot be refuted by inspecting only a finite prefix of a behavior; infinite state sequences must be inspected. As an example, consider a road intersection with a set of traffic lights.
A safety property S of the system might be: ``at all times no two
traffic lights will show green''. This property rules out ``bad'' things,
i.e. unsafe states; the occurrence of an unsafe state within an execution A simple liveness property of the traffic light example could state: ``every arriving car will eventually receive a green signal and cross the intersection''. The ``good'' thing here is the crossing of the intersection, and the term ``eventually'' refers to a fixed, finite but unknown time period. This relates to the formal definition of liveness as follows: consider the final state of some behavior prefix. In every such state it must still be possible to extend the execution so that this extension contains a ``good'' state (i.e., one in which the waiting car has passed). Other examples of safety properties are partial correctness, mutual exclusion and deadlock freedom. Conversely, examples of liveness properties comprise termination, eventual message delivery and starvation freedom. Safety properties state ``whenever the system performs a step, it is a good step'', while liveness properties can capture notions of progress (``the system will eventually perform a Page 671 step''). A state predicate Q implicitly defines a safety property denoted Prop(Q) which consists of all behaviors that start in a state satisfying Q. 2.2 Programs and SpecificationsAs noted above, a program A is viewed as a generator of behaviors. It consists of
The set of variables defines the state space of the program and state
predicate I describes the set of possible initial states. The state
transition relation is usually specified by a set of actions. An action
is often written in the form
Note that this execution model also encompasses the usual oneprocessor serial type of executions, where the program counter ensures that only one or (in case of a conditional statement) two actions are enabled. It has been generalized to also cover parallel and distributed systems. Formally, an action is a set of pairs of states and a set of
actions completely defines the state transition relation The liveness property L of the program defines what must eventually happen in a system execution. This will usually comprise some form of fairness meaning for example that every continuously enabled action must eventually appear as a state transition in an execution. Finally note that the set of behaviors generatable by a program A calculates to:
A program A satisfies a property p iff Prop(A) Page 672 2.3 RefinementIn a specification we would like to abstract away from the low level
implementation details of the underlying machine architecture. Thus, we
want state transitions of low level variables to appear as stuttering steps
in a high level specification. This leads to the notion of internal and
external variables. Think of V as being divided into two disjoint
sets Vi and Ve of variables called
internal and external variables, respectively. Now let the
internal variables be hidden from the state by a projection function This leads to the central concept of refinement. A program A2
refines a program A1 for function 2.4 Processes and CommunicationWhen modeling a distributed system we must in some form deal with the notion of a process. This can be done by partitioning the set of variables of a program at a given level of abstraction into n subsets, one for every process p1 pn . Usually this is done in such a way that for each pair of processes there exists a ``shared'' variable which is part of the state of both processes. Variables which are not shared are commonly called internal variables which is an indication that the abstraction of a process is closely related to the notion of refinement. (Consequently, shared variables are external variables of both processes.) Shared variables can be read by both processes. However, shared variables are further divided into input variables and output variables: a variable v shared between two processes pi and pj is an input variable of pi if it is only written by pj ; equally, if v is only written by pi we call it an output variable of pi. Intuitively, what is an input variable for pi is an output variable for pj. This usually signifies the direction of information flow between two processes. If a process is viewed as a subsystem in the sense defined in the introduction, then input and output variables form the interface of this subsystem. Communication is achieved between two processes by assigning/reading values to/from the output/input variables, respectively. This basic form is known under the name of synchronous communication. Using processes to model channels it is easy to see that also asynchronous communication (i.e. message passing) can be modeled. Page 673 2.5 Detection, Correction and Fault ToleranceWhen it comes to faulttolerance issues, there is some ambiguity in the literature on the meaning of the central terms fault, error and failure. Usually, a fault refers to a ``lowlevel'' defect in the system which may be physical (e.g. a bad memory cell which always returns a ``0'') or somewhat accidental (e.g. a programming mistake). A fault can cause an error which is a term of the system state, i.e. whenever a fault results in an abnormal change of the system state, an error occurs. Finally, we speak of a failure if a system deviates from its correctness specification [38, 28, 22]. Failures at some lower level of abstraction can again be faults on a higher level. There is strong evidence [19, 6, 7] that all fault tolerance mechanisms can be structured along the two distinct notions of detection and correction. Briefly spoken, detection means to observe a detection predicate P on the system state, and correction means to impose a correction predicate Q on the system (both notions seem to be formal equivalents of what is usually called error detection and error processing [38]). The abstract components used to achieve this functionality are called detectors and correctors (they are analogous to modules usually known as sensors and actuators). In fact it can be shown [6] that special forms of detectors and correctors are necessary and sufficient to achieve the usual types of fault tolerance. We will not define the term fault tolerance yet because there are various notions of fault tolerance. An intuitive understanding of fault tolerance as ``maintaining some form of correctness in the presence of faults'' suffices for the understanding of the following sections. In them, we will show how enhancing an originally faultintolerant program with faulttolerance components, as well as modeling the effects of physical faults can be seen and formulated as a transformation. 3 Transformations at the Subsystem LevelIn our context we will think of subsystems as being processes at a given level of abstraction that interact through their interface with other processes. 3.1 Program Transformation for Detection/CorrectionFirst we look at programs and investigate how adding faulttolerance components for detection and correction can be viewed as a program transformation. The starting point for all these methods is that a faulttolerant program can be always separated into a basic (i.e. fault intolerant) program and a set of faulttolerance components or modules. Early work on transformations for fault tolerance have focused on correction mechanisms, most notably the method of checkpointing with forward or backward recovery [41, 42, 53]. It was assumed that detection was done by ``lowerlevel'' hardware mechanisms that indicated a fault by raising a boolean flag. Upon fault detection, a recovery procedure would eventually be invoked which acted as a ``fault handler''. First, a program A must be transformed into a program that periodically takes checkpoints, i.e. it stores its state onto a form of available stable storage. Page 674 This can be done easily by doubling (or tripling) the variables and adding a timer to the program (such a timer can be implemented by reference to a realtime clock or by simply decrementing a counter after every state transition). When the timer expires, a subroutine is executed which stores the important parts of the program state into the replicated variables, and subsequently resumes normal operation of A. A checkpointing transformation C is given formally by Liu and Joseph [42, p. 154]. The checkpointing subroutine is an atomic action added to a program A. Due to the fair but nondeterministic choice of actions, the resulting program C(A) will take checkpoints after a finite time. In a different paper, Peled and Joseph [53] explicitly superimpose an interrupt mechanism and implement a ``timer interrupt handler'' that takes checkpoints at periodic intervals indicated by a lowerlevel timer component. They use two distinct sets of checkpointing variables to which the timer interrupt handler alternately writes its checkpoints. They also give a straightforward implementation of the handler procedure [53, p. 109]. As mentioned above, recovery is invoked when a boolean flag f indicating a fault is raised. Similar to the checkpointing transformation, a recovery action [42, p. 155] or a failure interrupt handler [53, p. 109] is invoked which restores the program state to the last checkpoint. The associated recovery transformation R adds the relevant recovery actions to the original program A and augments the liveness property of A in such a way that upon setting f, the recovery actions are eventually executed. Usually, the checkpointing/recovery variables are internal variables of the process and so they are not visible at the interface. While not naming it a transformation, Arora and Kulkarni [6] have explored similar approaches and have extended them also to fault detection. A detector d is an abstract (program) component which signals that some predicate P holds on the system state. Obviously, the precise implementation of d depends on P and so a general detection transformation must also depend on P. Analogously, the implementation of a corrector depends on the correction predicate Q which is to be imposed on the system state. Application of concrete program transformations using detectors and correctors appear in various case studies [8, 32, 7]. In general, these papers do not focus so much on the transformation aspect but rather on questions of completeness and modularity of the methodology. Also they stress that detectors and correctors must be designed in an interferencefree way, i.e. that they to not obstruct the ``normal'' behavior of the underlying program. Applications of detector and corrector transformations in the context of program synthesis have been studied by Arora, Attie and Emerson [4], where solutions to the mutual exclusion and the barrier synchronization problem are derived. This is done by deriving the necessary program transformations from the faults which are assumed to be in the system. Similar approaches which focus on a wellchosen failure assumption are, for example, described by Schlichting and Schneider [60], Schneider [61], Neiger and Toueg [48] and by Katz and Perry [31]. This shows, how important it is to have a detailed description of the faults that are deemed possible in the system. Ways of describing this in a transformational manner are described next. Page 675 3.2 Program Transformation for Fault ModelingAs noted above, some formalisms assume that the occurrence of a fault is signaled by raising a boolean flag f. This can be done by lowerlevel detection mechanism or (as also discussed above) by using a specific detector component at the same level of abstraction. If f is truthified by an underlying hardware detection mechanism, the change of f can also be viewed as the direct result of a fault together with its other (mostly unknown) effects on the program state. This leads to a formal approach to model faults and their effects in a transformational way. The idea behind this method is based on the observation that systems change their state as a result of two quite different event classes: normal system operation and fault occurrences [11]. Thus, a fault can be modeled as an unwanted but nevertheless possible state transition of a process. This state transition can be viewed as an additional action initiated by a (malicious) environment. As an example, consider a process which runs on a processor employed in some form of spacecraft. A problem influencing such objects in orbit is the radiation of cosmic rays which have a direct effect on electronic devices, especially volatile memory. In general, such rays can upset the contents of volatile memory and cause a transition to an arbitrary state. This is the classic example of a transient fault. It can be modeled by adding a state transition of the form
We call such an action a fault action. The idea of fault actions is usually attributed to Cristian [11]
but similar ideas appear also in a not so widely circulated paper by Echtle
[14]. The method has been incorporated into a transformational
approach by Liu and Joseph [41, 42].
In these approaches, the error flag f does not only signal a fault,
but it also disables all regular program actions of the program
A (not its recovery actions of course). This can be done by adding
This results in a fault transformation F as follows: a new ``error''
variable f is added to the set of variables of A and a special
set of fault actions is added to the set of actions. The guards of all
previously present (regular) program actions is augmented to contain The transformational approach has been generalized by Arora and Gouda [5], Liu and Joseph [44, 45], and Gärtner [17]. In these approaches, the faultaffected version of A results from simply adding a set of fault actions to the set of actions of A. This can be seen as the parallel execution of regular program actions of A with fault actions. In contrast to Liu and Joseph [44], it is argued by Arora and Kulkarni [7] and by Gärtner [17] that the introduction of auxiliary error variables into the state of A is necessary to be able to model all of the Page 676 common failure models from distributed systems theory (such as failstop [60], crash [21], general omission [55] or Byzantine [37]). As an example consider a process consisting of a single variable v and an action
We want to derive a version of this process under the crash fault assumption. This means that the process fails by simply stopping to execute steps forever. This can be modeled by introducing an additional boolean variable up and augmenting the process's code as follows:
Obviously, such a transformation can be formalized. However, the generality of this type of fault transformation must usually be restricted by additional ``global'' assumptions at the system level. As we are presently acting on the subsystem level, we will pick up this aspect again later (in Sect. 4.2). Formal examples of other fault transformations are given by Gärtner [17]. It should be noted that equivalent methods to model the effects of faults have also appeared using the formalism of Petri nets. For example, Girault [20] and Völzer [63] both describe how to model faulty behavior and reason about it by superimposing a special Petri net onto the representation of a program. 3.3 From Program to Specification TransformationsProgram transformations for detection, correction or fault modeling are not very useful on their own. Usually we want to reason about the transformed program and prove it correct with respect to some specification. It should be clear by now that this is in fact possible: explicitly incorporating faults into the program makes it possible to easily adapt the usual formalisms for reasoning about faultfree programs to now reason about their faultaffected counterparts. However, we need a specification to prove correctness. If we perform a program transformation onto a lowlevel program A, often the externally visible behavior will change. For example, if a process fault occurs and its execution has to be reset to the most recent checkpoint, all output operations at the interface that were performed after the checkpoint was taken will be repeated. We can obviously transfer the concepts of a transformation to the specification
level. However, since we are at a different level of abstraction, there
are different issues involved in this process. Peled and Joseph [53,
Def. 3.2] have introduced the useful notion of correspondence between
a program transformation and a specification transformation. A specification
transformation U corresponds to program transformation T
if U satisfies the following condition: for all programs P,
if P has a property Page 677
Figure 2: Definition of correspondence between U and T. 3.4 Specification Transformation for Detection/CorrectionAs mentioned above, detection and correction mechanisms will usually be hidden from outside observers by declaring their variables as being internal ones to the process. Also, it is often noted that faulttolerance mechanisms within a process should be totally transparent to the other processes when no faults occur. This means that the work of detection and correction mechanisms will usually appear as stuttering steps at the process interface. Sometimes it will be necessary to make detection mechanisms visible at the interface, for example when a process crashes and has been restarted, it is often useful for neighboring processes to know of this fact [3]. Thus, the specification of a process will then contain an additional ``epoch'' variable. Generally, detection and correction mechanisms must be reflected within the specifications of processes if they are part of ``larger'' detection and correction mechanisms, possibly at a higher level of abstraction. This is discussed in more detail when dealing with specification transformations at the system level in Sect. 4. But even if the detection/correction mechanisms do not appear at the process interface, introducing them will obviously transform a lower level process specification. At this level, detectors and correctors will appear in the form of their abstract specifications (as presented by Arora and Kulkarni [6]). Peled and Joseph [53, p. 111] give an example of such a transformation for the case of a backward recovery algorithm. The transformation can be divided into a fixed part Rf and a specification dependent part Rd. The fixed part Rf describes those properties of the added recovery module which are independent of the program to which they are added, so they do not directly alter its specification. The specification dependent part Rd of the transformation describes the interaction between the original program and the recovery module. (Note that the transformation does not refer to a particular program but to its specification.) For example, consider a simple database server. It's job is to receive query request messages sent by clients and respond to these messages by sending the requested item back to the client. The specification S of this server could be described as follows:
Assume there are faults that once in a while corrupt the state of the database, but these faults are detected by some lower level mechanism by raising some flag Page 678 f (i.e. we are only looking at the specification transformation for correction, not detection). How do the fixed part Rf and specification dependent part Rd of a checkpointing/recovery mechanism look like? The fixed part Rf will add to S something like the following two properties:
Note that these two properties are independent of S, i.e. they specify the specification independent part of R. As assumed, faults can lead to program states in which the integrity of the database has been destroyed. As this is detected immediately, there will be no ``incorrect'' responses of the server. However, any state specified by S may be ``wasted'' because a fault may occur before the next checkpoint is taken. The state is wasted because actions taken in this step must be reperformed. Also, in case of faults, a state may be delayed by recovery actions. This leads to the specification dependent part Rd of R. It states that any program state of S can be ``delayed'' by wasted states or recovery states. In general, Rd ensures that (after taking away the checkpointing states) the transformed program acts like the original program when wasted or recovery states are removed. (Formally, Rd is defined recursively on formulas of the specification language [53, p. 111].) Overall, the transformation R can thus be designated as
The effect of such a transformation on the visible behavior p
of the process can be evaluated when inspecting 3.5 Specification Transformation for Fault ModelingThe effects of faults on process specifications have been studied more widely than the effects of transformations for detection and correction. This is possibly due to the fact that the description of possible process failures is the starting point for any faulttolerance consideration. Like in specification transformations for detection/correction, transformations for fault modeling will usually weaken the specification of a process. We call this the enlargening behavior property of faults. Nordahl [50, p. 69] calls the resulting process specification a failure mode, others call it fault assumption [16], failure semantics [41, 12] or (in analogy to the term `faultaffected version') simply faultaffected behavior [42]. A failure mode may be formulated at design time (i.e. when discussing the anticipated fault scenarios) or at runtime (i.e. when engineers want to describe the observation of some faulty component). In many papers [50, 24] it is implicitly assumed that a failure mode is readily available. Obtaining a failure mode, i.e. specifying the specification transformation F, is however not easy. Page 679 But there are again obvious analogies to specification transformations for detection and correction. For example, Gärtner [18] presents a high level specification of the crash failure mode for processes pi as:
Like the specification transformations of Sect. 3.4, this describes a transformation F which can be separated into a fixed part and a specificationdependent part. Obviously F does not influence any safety properties of the original program A, but it will ``destroy'' all liveness properties. Others have described these transformations as proof rules in a verification calculus. For example, Joseph et al. [30] present a rule [30, rule R10] which makes it possible to derive an assertion about the ``failureprone process execution'' in the failstoprecover failure model. However, this proof rule only covers the safety properties of a process. Schepers [58, 59] also describes
the notion of a specification transformation and calls it a fault hypothesis
[58, p. 95]. A fault hypothesis is a reflexive relation
Note that the reflexivity of 4 Transformations at the System LevelAfter studying transformations at the process level, we will now turn to ``larger'' systems. However, as a process may be composed of many smaller components we can expect that many of the issues discussed in Sect. 3 will reappear in this section. However, the systems we will consider now can be thought of to be large and complex distributed systems consisting of many processes, and in fact there are several ``new'' issues which are of importance here. These are mainly concerned with compositionality. This means that for instance we would like to derive properties at the system level from properties at the subsystem level. (This should also count for transformations.) 4.1 Program Transformation for Detection/CorrectionIn large distributed systems without a common global time frame, different observers can come to different conclusions whether a predicate over the system state holds or not [62]. For simplicity (and for the sentence ``P holds globally'' to make sense), we will assume that there is a hypothetical global observer who can determine the truth of general state predicates instantaneously. But even if such an observer is postulated, practically imposing a correction predicate Q on Page 680 the system state or even detecting a predicate P is usually difficult and cannot be done atomically. Returning to the checkpointing/recovery transformations of Liu and Joseph [42] and of Peled and Joseph [53], this problem manifests itself in multipage expositions of the distributed recovery algorithms. In the distributed case, a global checkpoint must be constructed from multiple local checkpoints and the recovery algorithm must determine the most recent global checkpoint by piecing together local checkpoints. The concept that helps piece together local checkpoints and prove their usefulness is that of a consistent cut [9, 62]. Briefly spoken, a consistent cut is a collection of checkpoints describing a global state that does not violate causality (e.g. in which every message received has also been sent etc.). The local modules must engage in some form of correction protocol to reach agreement on the set of local checkpoints to use. The problems and complications encountered signify the intricacies faced when composing local concepts to global ones. But in general, this example shows that the local transformations of Sect. 3.1 can be composed to systemwide transformations. 4.2 Program Transformation for Fault ModelingLocal transformations of programs for fault modeling can also be generalized to global transformations in the obvious way that a local transformation is applied to every process of the system. However, this models only the local fault assumption which is not useful on its own. To see this, consider a distributed system with n processes running under the crash fault assumption. To model the effects of this assumption, the local crash transformation is applied to every process. Now obviously, this is a system in which all processes may crash; but if all processes may crash, the system cannot guarantee any liveness property. Thus, a global fault assumption is necessary that restricts the local transformations in a certain way. The terms local and global fault assumption were coined by Nordahl [49], but they have appeared before in many different shades. For example, it is often assumed that faults are restricted to a limited number of fault regions [22] (or fault locations). In practice these are assumptions like ``at most t < n processes may crash'' or ``at most one third of the processes goes Byzantine''. In general, it is necessary to have a finite error behavior assumption [40, p. 27], meaning one of the following requirements:
For example, the assumption that ``at most one third of the processes goes Byzantine'' assumes that 1. turning a process into a Byzantine processes can be done only finitely many times (here: at most n/3 times). This is captured by the first requirement. It is also assumed that Page 681 2. the fault actions of a Byzantine process cannot monopolize the system (i.e., the ``rest'' of the system must be able to perform state transitions and thus make progress while a Byzantine process is executing). This is covered by the second requirement. Without a finite error behavior assumption it is easy to show that achieving fault tolerance is impossible. Völzer [63] calls local fault assumptions the impact model of faults, and the global fault assumption the rely specification. The fundamental difference between both types of assumptions is that the former effectively adds behavior to a given system, while the latter restricts the additional behavior again. Both fault assumptions are always needed and must be applicable in the verification process to prevent unsolvability (like in the crash example from above). 4.3 Specification Transformation for Detection/CorrectionNaturally, the distinction between local and global requirements reappears also at the specification level. A composed lowlevel program transformation has the same notion of correspondence to a highlevel specification transformation at the system level as at the subsystem level (cf. Sect. 3.3). However, global requirements are reflected in the way how the local processes are connected or interact. Nordahl [50] introduces the concept of a design [50, p. 68]. For example, take a ring of processes which can pass a token via shared variables. Every process has a specification Si and the token ring has an overall specification S. The design of the token ring is the way in which the individual processes are connected (how input and output variables interact) to overall satisfy S, given that every process satisfies Si. Formally, a design for an nprocess system is a tuple consisting of n process specifications S1 , ..., Sn and a function C from Sn to S, where S denotes the set of all specifications. The mapping C is a combinator in the sense of CSP [25], e.g. parallel composition, union, or some composed construct. Note that C is not a specification transformation in the sense used throughout this article; it is merely a means to derive a global specification from local specifications. 4.4 Specification Transformation for Fault ModelingAs mentioned above, a specification S of a (faultintolerant)
system may not be solvable under a sufficiently hostile fault assumption.
However, adding fault tolerance components and some wellchosen design
may result in a system which satisfies a property close or equal to S.
A specification transformation F should reflect this and preferably
be able to derive the strongest specification Again, local transformations can be composed to global transformations. But we have discussed already in Sect. 4.2 that the global fault assumption needs to be encoded within the transformation as well. Recall that the set of behaviors of a system A can be described as
where I is the initial predicate, is the transition relation and L is the system's liveness property. The local fault assumptions, encoded as additional actions, Page 682 will usually add state transitions and augment
A result of Abadi and Lamport [2, Theorem 1] states, that Gl can be (and usually is already) incorporated into the system's liveness property L, so the global fault assumption will always be describeable as a safety property (this is conjectured by Gärtner [18] and implicitly assumed by Liu et al. [43, 44, 42, 45]). In result, the global specification transformation F can be characterized by the following equation:
As an example, consider a system consisting of n processes under
the crash fault assumption. Every process pi has
a local specification Si . We will assume that Si
is a safety property and that the process's liveness properties Li
are encoded in the system's liveness property L. In faultfree
executions the system is guaranteed to satisfy a specification S,
which is the composition
An implementation of a crash action within
and G would contain all behaviors where this action is executed on at most t processes. It is argued by Liu and Joseph [43, 44] (and more generally discussed by Abadi and Lamport [2, p. 94]) that the global fault assumption G can also be incorporated into the system's state transition relation . This seems clear since the alternative implementation of, for example, the crash action of a process could look like this: ``less than t processes have crashed'' This implementation incorporates G into Page 683 5 FaultTolerance Specification and Verification TechniquesThe previous sections have presented several different notions of transformations. This section now tries to answer the central question, how these transformations can help in the specification and verification of faulttolerant systems. First we will present some general definitions of fault tolerance and then consider specification and proof methodologies. 5.1 Definitions of Fault ToleranceA widely cited formal definition of fault tolerance was presented by Arora and Gouda [5]. It assumes that faults are modeled as a program transformation F . A system A is fault tolerant for a specification S if F(A) satisfies S. People confronted with this definition usually object and say that given some system A which satisfies S, F(A) will usually not satisfy S anymore due to the introduced faults. But this is exactly the decisive point of the definition: for S to hold for F(A), A must already contain fault tolerance mechanisms; faults from F are tolerated. The definition of Arora and Gouda [5] (which conforms with those of Liu and Joseph [41, 42] and Weber [64]) always refer to a complete system at a given level of abstraction. They do not explicitly deal with components and their interaction with each other. The distinction between the faulttolerance properties of subsystems and the fault tolerance of a design is made by Nordahl [50]. In his approach, a system is explicitly composed of n subsystems and a design. As mentioned in Sect. 4.3, a design is a description of how the components interact. A design C is called fault tolerant for a system specification S and a combination of subsystem specifications S1 , ..., Sn if C(S1 , ..., Sn ) satisfies S. This means that a faulttolerant design guarantees S if each component guarantees Si. (The definition is also implicitly used by Schepers [58].) Note that a design is fault tolerant with respect to a single combination of subsystem specifications S1 , ..., Sn. The individual S i can be an original subsystem specification or the weakened specification of a subsystem running under a fault assumption. To say that a design is fault tolerant with respect to a general fault assumption F , one must show that it is fault tolerant with respect to any possible combination of subsystem specifications allowed by F. For example, consider a ``hotstandby'' system consisting of two replicated servers A1 and A2 which each are able to provide a service according to some specification S to the outside world. Usually, server A1 runs and provides the service, but our fault assumption F states that at most one of the two servers may crash. If A2 crashed, service can continue normally. But to tolerate the crash of A1 , a coordination component is introduced which, after detecting the crash, will instruct A2 to take over the role of A1 . This is documented in the design of the hot standby system. Proving that the hot standby design is fault tolerant means to show that the composed system satisfies S in the three cases where (1) A1 and A2 satisfy S, (2) only A1 satisfies S and A2 has crashed, and (3) only A2 satisfies S and A1 has crashed. Note that the design is independent of the particular service which A1 and A2 are delivering so this approach makes it possible to abstract from a particular implementation of subsystems and restrict the attention to, e.g., the recovery protocol or redundancy mechanism used by the components. Page 684 Rushby [57] calls the approaches of the first type
(i.e. Arora and Gouda [5] and others) calculational
and those of the second type (i.e. Nordahl [50] and
others) specification approaches. Both approaches define fault tolerance
with respect to a specification 5.2 Specification and Proof MethodologiesTo rigorously prove that a system A is fault tolerant with respect to a specification S, we need a precise fault assumption (in the form of a program or specification transformation) and must check the validity of one of the definitions above by using some (formal) verification system. In the literature, there exist a variety of alternative methodologies to do that. 5.2.1 Using Traditional MethodsAs the effects of faults are modeled as regular program actions, the calculational approaches to the definition of fault tolerance [5] can use the same methods for the verification of faulttolerant systems than those used to reason about faultintolerant systems. This means that the approach will work independently of the underlying formalism. In the literature, TLA [34] (used by Liu and Joseph [44, 45]), CCS (used by Janowski [29]), and variations of Unity [10] (see Arora and Kulkarni [7] and Liu and Joseph [41]) have been applied. Specification methods can derive the validity of their proof rules from sound composition rules of the underlying formalism. Examples exist which build on CSP [25] (used by Joseph et al. [30], Nordahl [50] and Peleska [54]). The traditional methods have the advantage that they are well understood, people are wellcustomized with their application and so existing verification tools can be reused in the context of fault tolerance. However, it is a wellknown fact that introducing faults and faulttolerance mechanisms increases the complexity of the verification task substantially. And so specialized proof methods can be of use, as explained next. 5.2.2 Compositionally Complete Specification TransformationsPeled and Joseph [53] have introduced an interesting
proof method which builds on their definition of correspondence
between program and specification transformations. Recall that a program
transformation T and a specification transformation U correspond,
if all properties Although Peled and Joseph only discuss recovery transformations in this context, the proof rule can also be useful if T and U are transformations for Page 685
Figure 3: Idea behind Peled and Joseph's proof rule. fault modeling. For example, assume that T is some fault transformation and U is the corresponding specification transformation. It is now quite easy to see which properties of P are maintained under the fault assumption by applying U to them. It is not necessary anymore to ``calculate'' them from inspecting T(P). Analogously, assume T is some complicated recovery transformation.
Then we can first prove that P has a property 5.2.3 FaultTolerant RefinementIn the definition of Arora and Gouda [5], the fault transformation F is understood as a transformation at the program level. Liu and Joseph [41, 42] view F as a general formula transformation on a given level of abstraction. This makes it possible to extend the definition of fault tolerance to that of a faulttolerant refinement relation. This has resulted in a welldeveloped method for constructing provably
faulttolerant programs. Let A1 and A2
be two systems and F a fault transformation describing the faults
possible in A2. Then A 2 is an Ftolerant refinement
of A1 (denoted A1 Using the regular notion of refinement together with fault transformations
at different levels of abstraction, one can use a refinement calculus [1]
to derive faulttolerant programs from tolerance specifications as
follows: we start with a top level (tolerance) specification of some program
A0 . We must then refine A0 into a
suitable program A1 such that Page 686 At every level of abstraction, Fi will either change nothing (in the case of masking fault tolerance) or add an indication of faulty behavior (for example by weakening a component specification). If the latter takes place, we have reached a level of abstraction in which faults have a visible effect. At this point the refinement process must introduce measures which ensure that the refinement relation still holds, i.e. apply a transformation for detection/correction at that level. The methodology of faulttolerant refinement is very attractive since it transfers the paradigm of stepwise refinement [65] to the faulttolerance domain. This means that the complexity of proving fault tolerance is broken down into a lot of small and more manageable steps (see, for example, the case studies by Lamport and Merz [36] and by Peleska [54]). However, besides having to specify the fault assumption at many different levels of abstraction, we are faced with the same problems that usual refinement methods have to deal with, namely the cumbersome task of finding refinements and proving the refinement relation [1]. 5.2.4 MultitoleranceThe concept of multitolerance was developed by Arora and Kulkarni [7] in connection with their theory of detectors and correctors [6]. The idea of multitolerance is to divide the global fault assumption F into multiple and smaller fault assumptions Fi and handle them independently. For example, let F be the composition of two fault transformations F1 and F2 , i.e. F(A) = F2 (F1 (A)). Now considering F1 we can transform A into a suitable F1 tolerant A1 , which is obtained by applying an appropriate detector/corrector transformation T1 to A. The same transformation can be done to A1 regarding F2 resulting in an F2 tolerant A2 = T2 (T1 (A)). The construction process will guarantee certain properties of A2 dependent on the concrete realization of T1 and T2 . Additional proof obligations arise from the necessity to show the interference freedom of T1 and T2 , i.e. to show that T2 does not destroy properties introduced by T1 and vice versa. Formally, T1 and T2 must be shown to commute. 6 DiscussionMany of the techniques presented in the previous section use various different notions of transformations. Their exposition should have shown, that the distinction between system and subsystem level, as well as the distinction between program and specification was only made for expository purposes: systems are subsystems at higher levels of abstraction; equally, programs are specifications at lower levels of abstraction. Transformations can appear at any level in suitable forms. This is the first main point of this article: transformations are a general concept which is useful independently of the level of abstraction and the type of behavior which should be modeled. To separate concerns, transformations should be partitioned into a fixed part (which is independent of the transformed object) and a dependent part. Concerning compositionality, an aspect is to distinguish between the local part of a transformation (used for reasoning about components) and a global part (used to reason about the composition of subsystems). When applied to systems, the local part will be a general property and Page 687 the global part only a safety property. Generally, all notions of fault tolerance can be characterized by the statement, that a transformed version of a program must satisfy a transformed version of a specification. In calculational approaches, the effect of a fault transformation F onto the behavior of a system must be ``calculated''. This is sometimes difficult since a fault may only affect some small part of the system and the changes to the global behavior might not be evident. In specification approaches, these calculations are avoided by assuming a specification transformation which gives the faultaffected behavior of a component directly. Then, by compositional reasoning, the properties of the complete system can be derived. Hence, both methods can be combined: the calculational approach to derive degraded specifications of components, and the specification approach to reason about composed systems. However, it should be noted that research in reasoning about composed specifications has mostly only handled safety properties [58, 59, 30]. Trying to compose specifications that also contain liveness properties involves many intricacies and appears far from trivial [2]. Despite their obvious advantages, the difficulty of applying the methods described in the previous sections in practice must not be underestimated. This counts no matter whether mechanical verification is the goal or whether hierarchically structured, handwritten proofs are used [36, 35]. The examples which have been presented in the literature [50, 41, 42, 44, 45, 54, 36] have been small and academic. While the specialized methods of Sect. 5 may allow to lessen the complexity burden of faulttolerance considerations, they always impose additional proof obligations. Furthermore, it has been repeatedly underlined by Rushby [57] that formal methods (including those described in this survey) give no real evidence for attaching some reliability numbers to a system. Even if an algorithm has been verified to have a specific faulttolerance property, it is difficult to say actually how reliable the resulting system is. Also, faulttolerance properties are often jeopardized by malfunctions of the underlying operating system. Thus, formal methods can only be seen in complement with the usual methods of testing and fault injection [15, 26]. However, tools exists today which offer the possibility to realize the proof methodologies in practice. Most notably there are PVS [52], and recently also VSE [27], which seems especially useful because of its refinement mechanism. 7 Conclusions and Future WorkWe have presented a survey of methods to specify and verify faulttolerant systems which are based on a notion of transformations. Transformations are a general concept and almost anything where there is a notion of ``change'' can be formulated as a transformation. So it has been interesting to formulate fault tolerance methodologies which do not directly refer to the notion of a transformation (e.g. multitolerance [7]) within this framework. This seems to be an indication as if every verifiable faulttolerance method (e.g. failstop processors [60] or the state machine approach [61]) can be formulated in this way. Transformations offer the potential of being automated and often a transformation makes it possible to reuse many parts of an existing proof within a new (faulttolerance) context. Thus, transformational formulations can help aid the mechanical verification of faulttolerant systems. However, more case studies and experiences Page 688 are needed. Open problems stated by other authors are the effects of choosing open or closed systems on recovery transformations [53, p. 113] the problems of conjoining/transforming liveness properties [2, 53] and incorporating realtime into the formalisms and proof methods [44, 45, 36, 51]. How to systematically derive faulttolerance specifications from fault assumptions has also been described as difficult [50] and, despite general attempts [24] and case studies [18] has remained unsolved. Weber [64] noted in 1989 that the area of security might benefit from results in the faulttolerance domain, since the properties which have to be ensured seem similar. However, it has been argued [47] that many security properties are ``higherorder'' properties meaning that they cannot be expressed as sets of traces and thus fall outside of the safety/liveness domain. It is unclear whether there also exist similarly sensible higherorder properties in the domain of fault tolerance. Answers to all these questions are important, since they can potentially improve our understanding of the fundamental methods necessary to build dependable distributed systems. Acknowledgments We wish to thank Marc Theisen for clarifying discussions on specification transformations for fault modeling, and Henning Pagnia for reading an earlier version of this paper. Support by a grant from the Deutsche Forschungsgemeinschaft (DFG) as part of the ``Graduiertenkolleg ISIA'' at Darmstadt University of Technology is also gratefully acknowledged. References[1] M. Abadi and L. Lamport. The existence of refinement mappings. Theoretical Computer Science, 82(2):253284, May 1991. [2] M. Abadi and L. Lamport. Composing specifications. ACM Transactions on Programming Languages and Systems, 15(1):73132, Jan. 1993. [3] M. K. Aguilera, W. Chen, and S. Toueg. Heartbeat: a timeoutfree failure detector for quiescent reliable communication. In Proceedings of the 11th International Workshop on Distributed Algorithms (WDAG97), pages 126140, Sept. 1997. [4] A. Arora, P. C. Attie, and E. A. Emerson. Synthesis of faulttolerant concurrent programs. In Proceedings of the 17th Annual ACM Symposium on Principles of Distributed Computing (PODC'98), pages 173182, 1998. [5] A. Arora and M. Gouda. Closure and convergence: A foundation of faulttolerant computing. IEEE Transactions on Software Engineering, 19(11):10151027, 1993. [6] A. Arora and S. Kulkarni. Detectors and correctors: A theory of faulttolerance components. In Proceedings of the 18th IEEE International Conference on Distributed Computing Systems (ICDCS98), May 1998. [7] A. Arora and S. S. Kulkarni. Component based design of multitolerant systems. IEEE Transactions on Software Engineering, 24(1):6378, Jan. 1998. [8] A. Arora and S. S. Kulkarni. Designing masking fault tolerance via nonmasking fault tolerance. IEEE Transactions on Software Engineering, 24(6), June 1998. [9] Ö. Babaoglu and K. Marzullo. Consistent global states of distributed systems: Fundamental concepts and mechanisms. In S. Mullender, editor, Distributed Systems, chapter 4, pages 5596. AddisonWesley, second edition, 1993. Page 689 [10] K. M. Chandy and J. Misra. Parallel Program Design: A Foundation. Addison-Wesley, Reading, Mass., 1988. [11] F. Cristian. A rigorous approach to faulttolerant programming. IEEE Transactions on Software Engineering, 11(1):2331, Jan. 1985. [12] F. Cristian. Understanding faulttolerant distributed systems. Communications of the ACM, 34(2):5678, Feb. 1991. [13] E. W. Dijkstra. Guarded commands, nondeterminacy, and formal derivation of programs. Communications of the ACM, 18(8):453-457, Aug. 1975. [14] K. Echtle. Fehlermodellierung bei Simulation und Verifikation von Fehlertoleranzalgorithmen f¨ur Verteilte Systeme. In F. Belli, S. Pfleger, and M. Seifert, editors, SoftwareFehlertoleranz und Zuverlässigkeit, number 83 in InformatikFachberichte, pages 7388. SpringerVerlag, 1984. [15] K. Echtle and M. Leu. Test of fault tolerant distributed systems by fault injection. In D. Pradhan and D. Avresky, editors, FaultTolerant Parallel and Distributed Systems, pages 244251. IEEE Computer Society Press, 1995. [16] K. Echtle and J. G. Silva. Fehlerinjektion - ein Mittel zur Bewertung der Maßnahmen gegen Fehler in komplexen Rechnersystemen. Informatik Spektrum, 21(6):328336, Dec. 1998. [17] F. C. Gärtner. Specifications for fault tolerance: A comedy of failures. Technical Report TUDBS199803, Darmstadt University of Technology, Darmstadt, Germany, Oct. 1998. [18] F. C. Gärtner. An exercise in systematically deriving faulttolerance specifications. In Proceedings of the Third European Research Seminar on Advances in Distributed Systems (ERSADS), Madeira Island, Portugal, Apr. 1999. [19] F. C. Gärtner. Fundamentals of faulttolerant distributed computing in asynchronous environments. ACM Computing Surveys, 31(1):126, Mar. 1999. [20] C. Girault. Proof of protocols in the case of failures. In J. Evans, editor, Parallel processing systems. An advanced course, pages 121139. Cambridge University Press, 1982. [21] V. Hadzilacos and S. Toueg. A modular approach to faulttolerant broadcasts and related problems. Technical Report TR941425, Cornell University, Computer Science Department, May 1994. [22] W. L. Heimerdinger and C. B. Weinstock. A conceptual framework for system fault tolerance. Technical Report CMU/SEI92TR33, Software Engineering Institute, Carnegie Mellon University, Pittsburgh, PA, Oct. 1992. [23] M. P. Herlihy and J. M. Wing. Reasoning about atomic objects. In M. Joseph, editor, Proceedings of the Symposium on Formal Techniques in RealTime and FaultTolerant Systems, volume 331 of Lecture Notes in Computer Science, pages 193208. SpringerVerlag, Sept. 1988. [24] M. P. Herlihy and J. M. Wing. Specifying graceful degradation. IEEE Transactions on Parallel and Distributed Systems, 2(1):93104, Jan. 1991. [25] C. A. R. Hoare. Communicating Sequential Processes. PrenticeHall, 1985. [26] M.C. Hsueh, T. K. Tsai, and R. K. Iyer. Fault injection techniques and tools. IEEE Computer, 30(4):7582, Apr. 1997. [27] D. Hutter, H. Mantel, G. Rock, W. Stephan, A. Wolpers, M. Balser, W. Reif, G. Schellhorn, and K. Stenzel. VSE: Controlling the complexity in formal software developments. In Proceedings of the International Workshop on Applied Formal Methods, Boppard, Germany, 1998. [28] P. Jalote. Fault tolerance in distributed systems. PrenticeHall, Englewood Cliffs, NJ, USA, 1994. [29] T. Janowski. Bisimulation and FaultTolerance. Thesis, Department of Computer Science, University of Warwick, Coventry, UK, February 1996. Also University of Warwick Department of Computer Science Research Report CSRR300. [30] M. Joseph, A. Moitra, and N. Soundararajan. Proof rules for fault tolerant distributed programs. Science of Computer Programming, 8(1):4367, Feb. 1987. Page 690 [31] S. Katz and K. J. Perry. Selfstabilizing extensions for messagepassing systems. Distributed Computing, 7:1726, 1993. [32] S. S. Kulkarni and A. Arora. Compositional design of multitolerant repetitive Byzantine agreement. In Proceedings of the 18th International Conference on the Foundations of Software Technology and Theoretical Computer Science, Kharagpur, India, 1997. [33] L. Lamport. A simple approach to specifying concurrent systems. Communications of the ACM, 32(1):3245, Jan. 1989. [34] L. Lamport. The Temporal Logic of Actions. ACM Transactions on Programming Languages and Systems, 16(3):872923, May 1994. [35] L. Lamport. How to write a proof. American Mathematical Monthly, 102(7):600608, Aug./Sept. 1995. [36] L. Lamport and S. Merz. Specifying and verifying faulttolerant systems. In H. Langmaack, W.P. de Roever, and J. Vytopil, editors, Formal Techniques in RealTime and FaultTolerant Systems, volume 863 of Lecture Notes in Computer Science, pages 4176, Lübeck, Germany, Sept. 1994. SpringerVerlag. [37] L. Lamport, R. Shostak, and M. Pease. The Byzantine generals problem. ACM Transactions on Programming Languages and Systems, 4(3):382401, July 1982. [38] J.C. Laprie, editor. Dependability: Basic concepts and Terminology, volume 5 of Dependable Computing and FaultTolerant Systems. SpringerVerlag, 1992. [39] B. Liskov and W. Weihl. Specifications of distributed programs. Distributed Computing, 1:102118, 1986. [40] Z. Liu. Faulttolerant programming by transformations. PhD thesis, University of Warwick, Department of Computer Science, 1991. [41] Z. Liu and M. Joseph. Transformation of programs for faulttolerance. Formal Aspects of Computing, 4(5):442469, 1992. [42] Z. Liu and M. Joseph. Specification and verification of recovery in asynchronous communicating systems. In J. Vytopil, editor, Formal Techniques in Realtime and Faulttolerant Systems, chapter 6, pages 137-165. Kluwer, 1993. [43] Z. Liu and M. Joseph. A formal framework for faulttolerant programs. In C. M. Mitchell and V. Stavridou, editors, Mathematics of Dependable Computing, pages 131148. Oxford University Press, 1995. [44] Z. Liu and M. Joseph. Verification of fault tolerance and real time. In Proceedings of the 26th IEEE Symposium on Fault Tolerant Computing Systems (FTCS26), pages 220229, Sendai, Japan, June 1996. IEEE. [45] Z. Liu and M. Joseph. Specification and verification of faulttolerance, timing and scheduling. Technical Report 1998/5, Department of Mathematics and Computer Science, University of Leicester, U.K., 1998. [46] L. V. Mancini and G. Pappalardo. Towards a theory of replicated processing. In M. J. Warick, editor, Formal techniques in realtime and faulttolerant systems, volume 331 of Lecture Notes in Computer Science. SpringerVerlag, 1988. [47] J. McLean. A general theory of composition for trace sets closed under selective interleaving functions. In Proceedings of the 1994 IEEE Symposium on Research in Security and Privacy, pages 7993, Oakland, CA, 1994. [48] G. Neiger and S. Toueg. Automatically increasing the faulttolerance of distributed algorithms. Journal of Algorithms, 11(3):374419, 1990. [49] J. Nordahl. Specification and Design of Dependable Communicating Systems. PhD thesis, Department of Computer Science, Technical University of Denmark, 1992. [50] J. Nordahl. Design for dependability. In C. E. Landwehr, editor, Proceedings of the third IFIP International Working Conference on Dependable Computing for Critical Applications (DCCA3), pages 2938. SpringerVerlag, 1993. [51] J. S. Ostroff. Survey of Formal Methods for the Specification and Design of RealTime Systems. Journal of Systems and Software, 18(2):3360, Apr. 1992. Page 691 [52] S. Owre, S. Rajan, J. Rushby, N. Shankar, and M. Srivas. PVS: Combining specification, proof checking, and model checking. In R. Alur and T. A. Henzinger, editors, ComputerAided Verification, CAV '96, number 1102 in Lecture Notes in Computer Science, pages 411414, New Brunswick, NJ, July/August 1996. SpringerVerlag. [53] D. Peled and M. Joseph. A compositional framework for faulttolerance by specification transformation. Theoretical Computer Science, 128:99125, 1994. [54] J. Peleska. Design and verification of fault tolerant systems with CSP. Distributed Computing, 5(2):95106, 1991. [55] K. J. Perry and S. Toueg. Distributed agreement in the presence of processor and communication faults. IEEE Transactions on Software Engineering, 12(3):477482, Mar. 1986. [56] A. Pnueli. The temporal logic of programs. In Proceedings of the 18th IEEE Symposium on the Foundations of Computer Science (FOCS77), pages 4657, Providence, Rhode Island, Oct. 31Nov. 2 1977. IEEE, IEEE Computer Society Press. [57] J. Rushby. Critical system properties: Survey and taxonomy. Reliability Engineering and System Safety, 43(2):189219, 1994. [58] H. Schepers. Tracing fault tolerance. In C. E. Landwehr, editor, Proceedings of the third IFIP International Working Conference on Dependable Computing for Critical Applications (DCCA3), pages 3948. SpringerVerlag, 1993. [59] H. Schepers and J. Hooman. A tracebased compositional proof theory for fault tolerant distributed systems. Theoretical Computer Science, 128(12):127157, June 1994. [60] R. D. Schlichting and F. B. Schneider. Fail stop processors: An approach to designing faulttolerant computing systems. ACM Transactions on Computer Systems, 1(3):222238, Aug. 1983. [61] F. B. Schneider. Implementing faulttolerant services using the state machine approach: A tutorial. ACM Computing Surveys, 22(4):299319, Dec. 1990. [62] R. Schwarz and F. Mattern. Detecting causal relationships in distributed computations: in search of the holy grail. Distributed Computing, 7:149174, 1994. [63] H. Völzer. Verifying fault tolerance of distributed algorithms formally: An example. In Proceedings of the International Conference on Application of Concurrency to System Design (CSD98), pages 187197, Fukushima, Japan, Mar. 1998. IEEE Computer Society Press. [64] D. G. Weber. Formal specification of faulttolerance ad its relation to computer security. In S. Greenspan, editor, Proceedings of the 5th International Workshop on Software Specification and Design, pages 273277, Pittsburgh, PA, May 1989. IEEE Computer Society Press. [65] N. Wirth. Program development by stepwise refinement. Communications of the Association for Computing Machinery, 26(1):7074, Jan. 1983. Page 692 |
|||||||||||||||||
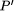 .
While
.
While 
 = s0, s1 ; s2 ...
of states from V. Finite state sequences are technically turned
into infinite sequences by infinitely repeating the final state. Sometimes
we explicitly deal with finite state sequences. We will call them behavior
prefixes or simply prefixes. The transition from one state to
the next state is called a step. If (si, si+1
) is a step and si = si+1 , then we
say that this step is a stuttering step.
= s0, s1 ; s2 ...
of states from V. Finite state sequences are technically turned
into infinite sequences by infinitely repeating the final state. Sometimes
we explicitly deal with finite state sequences. We will call them behavior
prefixes or simply prefixes. The transition from one state to
the next state is called a step. If (si, si+1
) is a step and si = si+1 , then we
say that this step is a stuttering step. 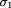 is equivalent to a behavior
is equivalent to a behavior 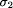 if they contain the identical sequence of states. Two behaviors
if they contain the identical sequence of states. Two behaviors 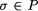 , then P also contains all behaviors which are stuttering equivalent
to
, then P also contains all behaviors which are stuttering equivalent
to 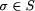 we thus conclude that no unsafe state occurs in
we thus conclude that no unsafe state occurs in  , and
, and 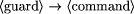 which is called a guarded command [
which is called a guarded command [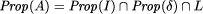
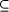 p (in this case we sometimes say that p holds for A).
A specification is a property which defines a set of ``intended''
behaviors of a program. A program A is correct with respect
to a specification S if A satisfies S.
p (in this case we sometimes say that p holds for A).
A specification is a property which defines a set of ``intended''
behaviors of a program. A program A is correct with respect
to a specification S if A satisfies S.  ,
i.e. for a state s,
,
i.e. for a state s, 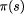 denotes the part of the state which refers to Ve only.
We can extend
denotes the part of the state which refers to Ve only.
We can extend 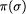 to be the sequence of states obtained by applying
to be the sequence of states obtained by applying 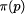 is called the set of external behaviors.
is called the set of external behaviors. 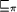 A2 or simply A1
A2 or simply A1  A2) if
A2) if 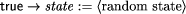
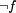 as an additional conjunct to the guards of all these actions. As long as
f = true, only actions from an additional set of fault actions
are active and can be executed.
as an additional conjunct to the guards of all these actions. As long as
f = true, only actions from an additional set of fault actions
are active and can be executed. 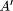 = F(A) is called the faultaffected version of A
(in general, the Faffected version of A). Note that
f may or may not be part of the observable system state: if lowerlevel
detection mechanisms exist, f is usually assumed to be a regular
program variable. But f may also simply be a variable of the mathematical
formalism used to reason about faultaffected processes, as described
next.
= F(A) is called the faultaffected version of A
(in general, the Faffected version of A). Note that
f may or may not be part of the observable system state: if lowerlevel
detection mechanisms exist, f is usually assumed to be a regular
program variable. But f may also simply be a variable of the mathematical
formalism used to reason about faultaffected processes, as described
next. 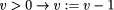
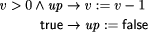
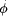 , then T(P) has the property U
, then T(P) has the property U 
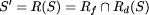
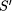 = R(S) will contain more behaviors. Thus, the specification
transformation will make S weaker.
= R(S) will contain more behaviors. Thus, the specification
transformation will make S weaker. 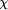 on process behaviors. Whenever a pair of behaviors
on process behaviors. Whenever a pair of behaviors 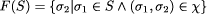
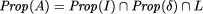
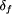 .
In general, the global fault assumption could be any property of the system,
i.e. a conjunction of a safety property Gs and a liveness
property Gl which must hold and thus are simply conjoined.
Thus the properties of the transformed program F(A) calculate to:
.
In general, the global fault assumption could be any property of the system,
i.e. a conjunction of a safety property Gs and a liveness
property Gl which must hold and thus are simply conjoined.
Thus the properties of the transformed program F(A) calculate to:
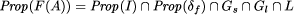
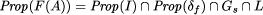
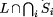 [2]. As we have argued above, the local fault assumption of crash will
transform any local liveness property Li of process pi
into
[2]. As we have argued above, the local fault assumption of crash will
transform any local liveness property Li of process pi
into 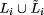 where
where 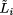 is the property describing that pi will eventually crash
(this is encoded in
is the property describing that pi will eventually crash
(this is encoded in 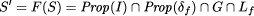
 ,
then
,
then 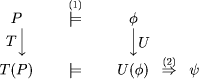
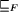 A2 ) if F (A2 ) refines A1
. Hence, A2 can be viewed as a ``faulttolerant version''
of A1 with respect to F.
A2 ) if F (A2 ) refines A1
. Hence, A2 can be viewed as a ``faulttolerant version''
of A1 with respect to F. 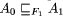 , i.e.
, i.e. 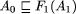 , where F1
is a fault transformation at that level of abstraction. (Remember that
a refinement step may introduce new internal variables and actions.) This
process can be repeated until a program Ak is derived
which is detailed enough to be turned into executable code.
, where F1
is a fault transformation at that level of abstraction. (Remember that
a refinement step may introduce new internal variables and actions.) This
process can be repeated until a program Ak is derived
which is detailed enough to be turned into executable code.