Symbol Ranking Text Compression with Shannon Recodings

Abstract In his work on the information content of English text in 1951, Shannon described a method of recoding the input text, a technique which has apparently lain dormant for the ensuing 45 years. Whereas traditional compressors exploit symbol frequencies and symbol contexts, Shannon's method adds the concept of "symbol ranking", as in `the next symbol is the one third most likely in the present context'. While some other recent compressors can be explained in terms of symbol ranking, few make explicit reference to the concept. This report describes an implementation of Shannon's method and shows that it forms the basis of a good text compressor.

Keywords text compression, Shannon, symbol ranking
Category E.4

1. Introduction

In 1951 C.E. Shannon published his classic paper on the information content of English text, establishing the well-known bounds of 0.6 - 1.3 bits per letter [Shannon 51]. What is perhaps less recognised is the method by which he obtained those results, and it is that which is used here as the basis of a text compressor.

Shannon actually describes two methods. In both of them a person is asked to predict letters of a passage of English text. Shannon also shows that the responses to the predictions are equivalent to the original text and that an "identical twin" or its mathematical equivalent could be used to recover the original input. In both cases the person effectively prepares a ranked list of the probable symbols, most probable first, and presents this list to the comparator.

1. In the first method, the person predicts the letter and is then told "correct", or is told the correct answer.
2. In the second method, the person must continue predicting until the correct answer is obtained. The output is effectively the position of the symbol in the list, with the sequence of "NO" and the final "YES" responses a unary-coded representation of that rank or position.

A third method is a hybrid of the two given by Shannon. After some small number of failures (typically 4 - 6) the response is the correct answer, rather than "NO". With some types of coding for the prediction values this may give a more compact code.

This algorithm is actually a transformation or recoding of the original text, with an output symbol for every input symbol. For his Method 2, Shannon gives the results reproduced in Table 1.

The distribution is very highly skewed, being dominated by only one value. This implies a low symbol entropy, which in turn implies excellent compressibility.

The technique used by Shannon is an example of the little known method of "symbol ranking". Statistical compressors usually rely on symbol frequency, to assign shorter codes to more frequent symbols, and symbol contexts, to restrict the choice of probable symbols and enhance the symbol frequency encoding. Symbol ranking simply takes the current context (or any other aid to compression) and, based on that, prepares a list of all possible symbols, ordered from most likely to least likely. The recoding of the symbol is its position in the ordered list. The sequence of operations is then contexts ranked-list encoded output. Because of its historical antecedents, the coding into the ranked list will be called a "Shannon coding". This is not to be confused with the well known Shannon variable-length code, which may of course be used to finally encode the output.

"All that is needed" to implement a compressor is some algorithm which can produce a symbol list ranked according to the expected probability of occurrence, with a following statistical compressor.

2. History of symbol ranking compressors

Several compressors can be seen as implementing the methods of symbol ranking, but with little reference to Shannon's original work. An early example is the MTF compressor of [Bentley et al 86], which uses words rather than individual characters as its basic compression symbols. [Lelewer and Hirschberg 91] describe the use of self-organising lists to store the contexts in a compressor derived from PPM.

[Howard and Vitter 93] also follow PPM in developing a compressor, but one which explicitly ranks symbols and emits the rank. They show that ranking avoids the need for escape codes to move between orders, and also describe an efficient "time-stamp" exclusion mechanism. Much of their paper is devoted to the final encoder, using combinations of quasi-arithmetic coding and Rice codes. Their final compressor has compression approaching that of PPMC, but is considerably faster.

A more important recent example is the "block sorting" technique (or "Burrows- Wheeler Transform - BWT) described recently by [Burrows and Wheeler 94], and extended by [Wheeler 95] and [Fenwick 96a, Fenwick 96b]. It uses a context dependent permutation of the input text to bring together similar contexts and therefore the relatively few symbols which appear in each of those contexts. A Move- To-Front transformation then ranks the symbols according to their recency of occurrence. Overall, the result is very similar to what is obtained here, except that the input is permuted in block sorting, whereas here it is processed in its natural order.

[Fenwick 96b] shows that block sorting is a symbol-ranking compressor, with the

Move-To-Front list acting as a good estimate of symbol ranking. In collecting together similar contexts, the preceding sort phase also brings together the symbol rankings of those contexts; because the contexts are similar so are the ranking lists and the list for one symbol is usually a good prediction of that for the next symbol.

More importantly, the initial transformations of the block-sorting compressor and the symbol recoding of the new method both produce highly skewed symbol distributions. Methods which were developed for the efficient coding of the block sorting compressors are applicable to the new method as well. It will be seen that the frequency distributions of the recoded symbols are very similar for the two cases.

In comparison with PPM, the other major family of context-dependent compressors, the major differences are that here there is no attempt to assign probabilities to explicit symbols in each context and no need to use an escape symbol to move between context orders.

3. The algorithm

[Bloom 96a] has recently produced a family of compressors based on the one simple observation that the longest earlier context which matches the current context is an excellent predictor of the next symbol. His compressors follow Shannon's first method in that he flags a prediction as "correct" or "incorrect" and follows an incorrect flag by the correct symbol. His compressors differ in their manner of encoding the flags and of presenting the correct symbol, with some giving moderate compression at very high speeds and others giving exceedingly good compression (as good as any reported) albeit with slower performance.

His method is essentially one of statistical sampling. The most recent matching context acts as a randomly chosen context when the whole file is considered, although probably biased by recency or locality effects. Thus while his method does not guarantee to deliver the most probable symbol, it is quite likely to deliver it or, failing that, will deliver one of the other more probable symbols.

The algorithm presented here extends Bloom's method to offer possible symbols in the approximate order of the probability of their occurring in the present context. Although based on probabilistic sampling it is completely deterministic and is equally applicable to both compression and decompression. The visible technique is exactly that of Shannon's second method-symbols are offered as candidates in the order of their estimated likelihood and the number of unsuccessful offers is encoded. The algorithm proceeds in several different stages -

1. The preceding data is searched for the longest string matching the current context (the most-recently decoded symbols). The symbol immediately following this string is offered as the most probable candidate. So far this is precisely Bloom's algorithm. The search may be terminated as soon as strings match to some predetermined length, or order, or the search may proceed to an unlimited match length (unbounded order).
2. If the first offer is rejected, the search continues at the original order, looking for more matches which are not followed by the first-offered symbol. The first such

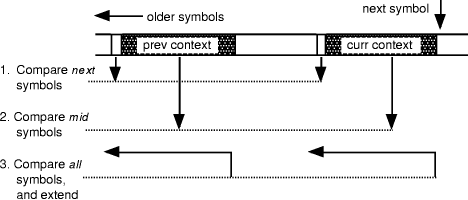
Page 72

---

following match is the second offered symbol. If that suggestion is rejected, the search continues along earlier contexts of the same order. As the search proceeds, symbols which have been rejected are added to the exclusion list as candidates which are known to be unacceptable.

3. When all available contexts have been searched at an order, the order is reduced by one and the search repeated over the whole of the preceding text, from most recent to oldest. Matches followed by an excluded symbol are ignored and any offered symbol is added to the exclusion list.
4. When the order has dropped to zero, the remaining alphabet is searched, again with exclusions. This copy of the alphabet is kept in a Move To Front list, rearranged according to all converted symbols to give some preference to the more recent symbols.

The algorithm described was originally developed as a "proof of concept" rather than a production-level compressor. It works well on smaller and more compressible files but is slow and gives poor results on larger or less compressible files where there is more text to search and more samples are likely to be rejected. Section 8 describes improvements which bring its speed more into line with accepted statistical compressors.

The decompression algorithm is the obvious converse. An initial statistical decoder recovers the sequence of symbol ranks and the symbol prediction mechanism is then called, rejecting as many estimates as indicated by the rank.

4. Implementation

The context-analysis algorithm is implemented using techniques derived from sliding- window LZ-77 parsing and with a fast string-matcher similar to that devised by Gutmann [Fenwick 95].

Exclusion is handled by the method of Howard and Vitter, using a table of the contexts in which each symbol was last offered. When a symbol is first considered as a candidate, its current context is compared against that in the table; if the two match the symbol has been already considered within this context and must be excluded. The context of a non-excluded symbol is then saved before the symbol is offered. The table contains the position of the last context symbol and is indexed by the test symbol.

4.1 Finding the initial offering

The context discovery mechanism uses a fast string comparison technique similar to one initially designed for LZ-77 compressors. The known text is saved in a wrap- round sliding window buffer, with pairs of "similar" digraphs linked as a list to facilitate fast traversal; the lists are accessed via a hash table on the last two symbols. The mechanism is shown in Figure 2.

Assume at some stage that we know a context which matches "curr context" to some length and have linked to the next possible context ("prev context").

• The rightmost (most recent) symbols of the two contexts probably match because they share the same hash value.
• As we wish to extend the match to find a longer context we first test the symbol beyond the known best order. If this differs the context cannot possibly extend. Choosing this symbol also uses one which is less correlated with the most recent symbols.
• Having confirmed that the extension symbols match, we compare two symbols near the midpoint of the two contexts, as a further quick filter on the contexts. On some files it is better to compare low probability symbols at about the midpoint, but it is usually simpler to use the actual midpoint.
• Finally we do a complete string comparison, from the most recent symbols, for as long as the contexts match. If this extends the contexts the test context becomes the best-known and its order is saved as the best order.

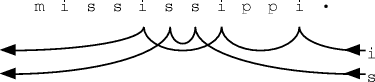
Experience is that 50% of the possible contexts are eliminated by the first, extension, test and that fewer than 10% survive the midpoint comparison and need a full string compare.

From this string comparison algorithm we find the longest preceding context which matches the most recent context; the symbol following that context is offered as the first choice. We also enter this symbol in the exclusion table in case a longer search is needed.

4.2 Continuing within the order and to lower orders

The algorithm for continuing the search is similar in spirit but different in detail. The search is now at a known order, with the initial test on the end-symbol of the context, not on the one beyond the end, and the comparison never extending outside the limits defined by the current order. At an early stage of the tests, and certainly before the complete string comparison, the following symbol is tested against the exclusion table. The next symbol with a matching context and which is not excluded is offered as the next candidate symbol.

When the oldest available context has been tested at a particular order, the order is reduced by one and the search repeated from newest to oldest. At no stage is the order actually released to the coding mechanism. All that is released is the possible symbols, in the expected order of likelihood.

4.3 Handling order-1 contexts

With two symbols used in forming the hash value, the above methods do not work for order-1 contexts. These are handled by a completely different mechanism. For each context (or most recent symbol) there is a series of links along the buffer, linking occurrences of that symbol, but bypassing occurrences where the following symbol has been seen already in that list.

For tracing an order-1 context the appropriate list is selected according to the context symbol and its list traversed. The next symbol which is not excluded is offered as the next candidate (the list structure automatically maintains order-1 exclusions.) The technique is illustrated in Figure 3.

Two lists are shown, for the context symbols "i" and "s". (The lists for "p" and "m" add nothing to the explanation.) In order from the rightmost (most recent) symbol, the "i" list links occurrences followed by, in order "", "p" and "s". The leftmost "i" of the string is followed by an "s". This symbol has already been seen and is therefore bypassed. The "s" list similarly bypasses the leftmost two "s"s, both of whose following symbols have been already seen.

Whenever a new context is created the list is traced to find the occurrence of its following symbol. The list is then altered to bypass that older occurrence because it has been superseded by the more recent occurrence. This implements exclusion within the list and also limits the length to be searched.

5. The statistical coder

Two arithmetic coders have been used in producing the following results. The first is a simple "Order-0" coder which just adapts to the symbol frequencies without regard to context. It must however resolve mutually contradictory requirements.

• The coder must handle an alphabet of about 256 symbols

Page 75

---

• The symbol frequencies cover a range of about 4 orders of magnitude, requiring a maximum count of some tens of thousands and a similar ratio between the maximum count and the increment for each symbol.
• The considerable local variation of symbol statistics requires a very "agile" coder, which in turn requires a low ratio of maximum count to increment and a small alphabet.

These conflicts are resolved with a "structured" coder [Fenwick 96b], in which a first- level coding model handles rank values in approximately octave groups {0, 1, 2...3, 4...7, 8...15, ..., 128...255}. Most groups have second-level models to encode symbols within the groups. The first-level model has only nine symbols and the first few second-level models are similarly small to allow fast adaptation to local changes in frequencies.

If the ranks had frequencies proportional to rank ^-1 the groups would have equal loadings. Even though the actual variation is closer to rank ^-2 , the structure seems close to optimum.

6. Compression Results

Results for the compressor are shown in Table 2, tested on the Calgary compression corpus¹ . All of these results include two techniques developed for block sorting compression.

• The input text is subject to run compression, with runs of length 6 or greater being replaced by the initial 6 symbols and then a length count coded into following symbols. This is intended primarily to increase the speed of encoding files such as PIC, which have many long runs and compress very slowly. A threshold of 6 means that most files are not affected. This run compression does improve the compression of PIC by about 10%.
• The output of the Shannon coder has a preponderance of 0's (first prediction correct) and most of these occur in runs. These are run-length encoded using a method due to Wheeler [Wheeler 95, Fenwick 96b] to give a small improvement in the compression of all files.

The block sorting compressor is used as a comparison because of its close relationship to the new symbol ranking compressor. Both are "symbol ranking" compressors, but block sorting permutes the input file whereas the symbol ranking compressor works on the file in natural order.

The rightmost columns are for various versions of the new "symbol ranking" compressor.

1. 64 K buffer, Order-0, maxorder=20. The sliding window buffer is 64 Kbytes long (the most recent 65,536 bytes enter into context determination), the output is encoded with a simple order-0 arithmetic coder, and the maximum context

---

¹The files of the Calgary compression corpus are available by anonymous FTP from ftp.cpsc.ucalgary.ca: /pub/projects/text.compression.corpus/ textcompression.corpus.tar.Z

Page 76

---

order is 20. This is intended as a reference version of the new symbol ranking compressor.

File Block Sort, Order-0 Block Sort, structured BIB 2.31 1.95 BOOK1 2.52 2.39 BOOK2 2.20 2.04 GEO 4.81 4.50 NEWS 2.68 2.50 OBJ1 4.23 3.87 OBJ2 2.71 2.46 PAPER1 2.61 2.46 PAPER2 2.57 2.41 PIC 0.92 0.77 PROGC 2.67 2.49 PROGL 1.84 1.72 PROGP 1.82 1.70 TRANS 1.60 1.50 Average 2.53 2.34

64 K buffer Order_0 maxorder=20 1024 K buffer Order-0 maxorder=20 64 K buffer structured maxorder=20 1024 K buffer structured maxorder=20 2.31 2.26 2.27 2.22 3.06 2.85 3.03 2.82 2.52 2.35 2.48 2.32 5.72 5.71 5.51 5.49 2.89 2.66 2.84 2.62 3.94 3.94 3.79 3.79 2.63 2.50 2.55 2.43 2.63 2.63 2.59 2.59 2.72 2.71 2.69 2.68 0.84 0.83 0.84 0.82 2.60 2.60 2.55 2.55 1.74 1.74 1.70 1.70 1.73 1.73 1.69 1.69 1.54 1.51 1.50 1.48 2.63 2.57 2.57 2.51

Table 2. Results in compressing the Calgary Corpus, values in bits/byte

2. 1024 K buffer, Order-0, maxorder=20. The buffer size is now adequate to hold the largest files and allows contexts from the whole file rather than just the most recent 64 K bytes. As compared with the previous column, the improvement is up to 8% for the larger files. (Many of the smaller files fit, completely or nearly, into the smaller buffer and show little or no benefit from the larger buffer. The initial run-encoding of PIC transforms it into a file of little more than 100 Kbyte and it behaves here as medium-sized file.)
3. 64 K buffer, structured, maxorder=20. The coder has been replaced by the "structured model" described above in Section 5.
4. 1024 K buffer, structured, maxorder=20. This case combines the benefits of the larger file for more context information and the improved final coder.

A test with a 64 K buffer, structured coder, and maxorder=10 gave somewhat somewhat faster operation, but slightly poorer compression than the similar one with maximum order = 20 (2.59 bit/byte).

The results are generally similar to those with block sorting, which is of course to be expected from the similarity of the two methods. In general the new compressor seems to be better on the object files and the more compressible text files, while block sorting is better on most text files and much better on GEO.

The difference probably arises from the sampling symbol predictor in the symbol ranking compressor. While it works well for compressible files where there is little doubt as to the correct symbol, for less compressible files there tend to be more "reasonable" symbols and a correspondingly greater chance of making a poor prediction.

7. Use of fixed codes

An interesting comparison is to replace the final statistical compressor with a much simpler equivalent to compare both the compression performance and the compression speed. The chosen code is the [Elias 75] code which is simple to generate and generally matched to the symbol distributions found here. The code for an integer has the data bits in reverse order (least-significant first), with most preceded by a "flag" bit of 0. The final bit (the most-significant 1) is omitted but has a flag of 1. A rearrangement of the bits gives the code, which has the normal binary representation of the integer, preceded by a 0 for each bit after the most-significant 1. The prefix is therefore a unary coding of the length. A bias of 1 is needed to allow a value of 0 to be represented.

The "structured" model was replaced by a simple order-0 model without run-encoding of the symbol ranks. (Input run-encoding was retained as it has no effect on the final coding and accelerates compression of some files.) Both coders are then handling values of 0-256 (256 symbols plus End-Of-File). The removal of run-encoding gives rather poorer compression on many files, even with the arithmetic coder.

The tests were run on a HP 755 workstation, for the smaller files of the Calgary Corpus and with a sliding window of 512k. The code is about 3% faster than the arithmetic code showing that the relatively slow arithmetic coder contributes little to the overall time. Most of the effort is in finding the contexts and sampling their predicted symbols. The text files are handled well by the code, being within 2.5% of the arithmetic code. GEO and OBJ1 (less compressible) and TRANS (more

compressible) are poorly matched to the Elias code. Also shown in Table 3 are comparable figures for BZIP (a block-sorting compressor) and GZIP (a reference high performance compressor, at level-9 compression). The relative speeds with arithmetic and codes are in line with the author's experience with compressors such as BZIP. The impression was that time in BZIP is about equally divided between the initial analysis and the final coding. The difference between the arithmetic and g codes is comparable to half the time for BZIP, given the probable timing resolution.

A "punctured" variant of the code gives better performance on GEO [Fenwick 96c]. The bits are still written in reverse order, least-significant first, but the 1's and only the 1's are followed a flag bit which is 1 after the most-significant 1 (the last data bit) and 0 elsewhere. Small values are slightly longer but larger ones require an average of only 75% of the bits of a normal code. The lengths are a good match to the rank distribution for GEO and the punctured code improves its compression by about 7%.

8. Acceleration of the Compressor

From Section 7 it is clear that most of the execution time is spent in parsing the input, searching the window to analyse the contexts and determine likely symbols for offering as candidates. The analysis is very similar to that performed by PPM except that PPM needs explicit symbol probabilities, whereas here we need only a ranked order of symbol probabilities. Howard and Vitter based their compressor on a conventional PPM trie data structure, whereas the approach here is superficially quite different. A great deal of time is spent in searching the window for contexts and usually rejecting that context because its following symbol is excluded. As high-ranked symbols may occur with a likelihood of less than 0.1%, hundreds or thousands of contexts and symbols may be rejected for each that is even offered as a candidate. Although the frequency of such action is quite low, its cost is high and the final effect is significant.

In this section we address the speed of the parsing step as this is obviously the main limitation on compression speed. The scheme as described so far uses a set of three parallel arrays

1. The input text itself.
2. A series of links between digraphs with the same hashing value, used to accelerate traversal of the first array.
3. A series of links, one for each symbol value, which are sensitive to the following symbol. Each link bypasses cases where the following symbol has been already seen, to handle order-1 with exclusion.

Several attempts were made to accelerate the searching. All are mentioned here, including one which was less successful.

1. Trigraph links. The list of "hashed digraphs" is supplemented by lists of true trigraphs. The window scan starts using the digraph list, but as soon as the contexts extend to order-3, control is transferred to the trigraph list. This change reduces the number of tests needed at high context orders and approximately doubles the overall speed compared with the original.

Page 79

---

2. Order-5 contexts. The order-3 list is supplemented with an order-5 list, handled in a similar fashion, with the order of this list chosen by experiment. The order-5 list gives a further 30-40% improvement over the order-3 list.
3. Order-2 exclusions. An order-2 exclusion list, similar to the order-1 list, was an obvious possibility. The costs of building the list outweighed its benefits; it slowed execution by about 5% and was abandoned.
4. Fast rank-0 prediction. Much of the output consists of a series of rank-0 predictions and most of these are seen to "lock on" to a context which extends by one as each symbol is processed. If the last symbol was handled at rank-0, we can eliminate context searching by just looking at the symbol following the last context and predicting that as the next symbol. This works as long as the context order is less than the maximum. Consider the case where the input contains "...the word is ..." and, more recently "...a word can..." and the text to be matched is "...the word can..." with a maximum context order of 6. The initial context is the first phrase, but the context will transfer to the second phrase as soon as " word " has been processed, with no external indication of the change. The simple fast prediction, locked to the first context, would predict "is" instead of the correct "can". To avoid continuing with the wrong context, fast prediction must be inhibited as soon as the context order reaches its maximum. For most files about half of the fast rank-0 predictions are correct and the average speed benefit is about 10%.

Elias File bit/ byte old time new time fast Rank-0 bib 2.51 61.6 19.2 16.3 geo 6.48 139.7 40.6 40.0 obj1 4.45 3.5 2.8 2.7 paper1 2.74 16.6 6.3 5.2 paper2 2.78 49.7 12.4 11.3 progc 2.75 9.6 4.3 3.8 progl 2.03 31.2 9.6 8.2 progp 2.04 17.8 7.5 6.2 trans 1.97 32.2 13.2 11.4 TOTAL 362 116 105

PPMZ bit/ byte time secs 1.80 9.1 4.64 20.7 3.72 11.1 2.29 3.3 2.29 6.2 2.32 2.5 1.52 5.8 1.57 4.7 1.28 6.2 70

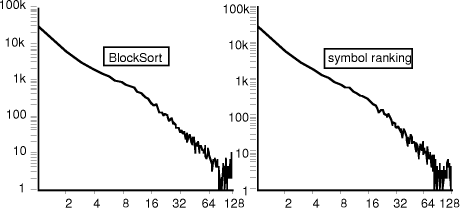
Table 4. Compression speeds on smaller Corpus files

The lists are all stored as 16-bit displacements back to the earlier element of the list. If the window is larger than 64 K bytes and the displacement exceeds 65,535 that particular list is assumed to have ended; older elements are forgotten. Each input symbol needs one byte to store its own value and 4 16-bit link values, to a total of 9 bytes per data byte.

Table 4 gives the speed with these changes, for the smaller corpus files, showing the previous time, the time with order-5 contexts, and the time with fast rank-0 prediction,

all with the Elias g coding. Overall, these changes reduce the running time to about 30% of the original, bringing it much closer to that of other good compressors. Included in Table 4 are values for the PPMZ compressor of [Bloom 96b], the best one known to the author, with all times measured on a HP-755. The symbol ranking compressor is generally about half as fast as PPMZ, but may be considerably faster on some large files. PPMZ has a running time of some hours on the file PIC, but under 2 minutes with the sliding window parser.

9. Block sorting, symbol ranking and PPM.

While block sorting (BWT) and symbol ranking compression may be regarded as generally equivalent, they do give slightly different results. Figure 4 shows the frequencies of the symbol ranks for the file PAPER1 using the two methods. At this scale the two are essentially identical, except for minor differences for ranks beyond about 16 where the symbol probabilities are quite low.

Until now we have used 0-origin numbering for the ranks with the most frequent being rank-0. For this section it is more convenient to use 1-origin numbering, starting from rank-1, because it allows taking logarithms of the ranks.

128 64 32 16 8 4 2 symbol ranking 100k 10k 1k 100 10 1 100k 10k 1k 100 10 1 128 64 32 16 8 4 2 BlockSort

More detail can be seen in Table 5 which shows the relative frequencies of symbol ranks for the two compressors, for the relative frequencies greater than about 1%. The more-probable values (ranks 1, 2 and 3) are slightly more frequent with symbol-ranking compression; this lowers the skewness of the distribution and degrades the compression slightly.

The symbol frequencies of Figure 4 very nearly follow a power law (freq(n) = n -2 ). The exponent is close to 2 for most text files, is higher for more compressible files and lower for less compressible files. The Elias code is optimum for an inverse square distribution and the punctured code for n ^-1.5 . The Rice codes used by [Howard and Vitter 93] are however much better for exponential distributions (freq(n) = x ^-n ) and are ill-suited to a power law distribution of symbol frequencies.

Another effect which is not visible from these results comes from the locality effects of block sorting. Block sorting collects together similar contexts and emits the symbols from those contexts in sequence. Because the contexts are similar so are their symbol rankings and ranking frequencies. A suitable final coder can adapt to the local statistics of the contexts. Block sorting (or Burrows-Wheeler Transform) combines a very efficient context analysis in its initial sort phase with a good running approximation to symbol ranks and rank frequencies, even with no knowledge of the actual contexts.

The symbol ranking compressor by comparison must switch between quite different contexts for successive symbols and cannot adapt to any of them. This is probably the major reason for the difference in the results. When this paper was first prepared, the author intended to investigate symbol ranking compressors based on explicit context dictionaries and some other techniques which would have allowed coding models for individual contexts. While these worked, they gave no advantage in speed or compression over that described here and are accordingly ignored.

Symbol ranking initially seemed to have the great advantage over PPM that it avoids escapes to lower-order contexts and the calculation of escape probabilities. Recent advances in PPM compression, as in the PPMZ compressor of [Bloom 96b], have largely overcome the problems of escape probability. Of more importance though is that symbol ranking codes just the ranks; the probabilities must be derived from the rank frequencies and these probabilities strictly belong to individual contexts rather than averaged over all contexts. Explicit probabilities are available with some parsers, but using them directly without deriving symbol ranks leads directly to PPM!

10. The prediction process

Some output from an actual encoding of a version of this paper is shown in Figure 5. There is a 2-symbol overlap between the two sequences. The actual text is written in bold face, with the output value just below it (this is the number of wrong estimates for the symbol). Above each symbol are the predictions for that symbol, with the first always at the top. The eighth and subsequent bad estimates are replaced by a single . Below the output code is the order at which that code is determined, often with an

obvious relation to the preceding text.

What is not so easily conveyed is the way that the order changes during prediction. For example, in predicting the final "e" of "Shannon code", the unsuccessful "i" is predicted at order 11, but the next prediction (successful) is at order 4, with no external indication of the change in order.

While there is often some difficulty in establishing a symbol, the correct text then often proceeds with no trouble for several symbols. A human predictor would get "of" with little difficulty, and should also get "Shannon" almost immediately from the overall theme. Again, the latter part of "preponderance" should be predictable (there is no other reasonable word "prepon...") The prediction is often almost eerily like that expected from a person, but with a limited vocabulary and largely ignorant of idiom. (This text, of about 21,000 bytes, compresses to 2.77 bit/byte.)

11. Final Comments

The algorithm described here was initially intended to illustrate the principle of symbol ranking compression and to test the feasibility of extending Bloom's LZP techniques to higher symbol ranks. To that extent it is quite successful and, with the enhancements described in Section 8, runs at a reasonable speed for a statistical compressor, though not at the speeds or compression of good PPM implementations.

The present work on symbol ranking arose from consideration of the block sorting (BWT) compressor with a view to overcoming perceived disadvantages in the block- sorting algorithm. The discussion in Section 9 though shows that these disadvantages were more apparent than real and that the BWT algorithm is a very efficient implementation of symbol ranking.

Symbol ranking is best seen as an historically important technique which relates several apparently disparate compression methods and underlies the operation of some new and powerful recent compressors such as those of Burrows & Wheeler and of Bloom.

Acknowledgements

This work was supported by research grant A18/XXXXX/62090/F3414032 from the University of Auckland and performed while the author was on Study Leave at the University of Western Australia. The author acknowledges the contributions of these institutions. Thanks are also due to Prof. David Wheeler, whose work on the block sorting compression algorithm led the author into the present work, and to Charles Bloom, whose LZP compressors provided the direct inspiration. Finally, several improvements were suggested by the referees.

References

[Bentley et al 86] J.L. Bentley, D.D. Sleator, R.E. Tarjan, V.K. Wei. "A locally adaptive data compression algorithm", Communications of the ACM, Vol 29, No 4, April 1986, pp 320-330

[Bloom 96a] C. Bloom, "LZP: a new data compression algorithm", Data Compression Conference, DCC'96

[Bloom 96b] C. Bloom, private communication

[Burrows, Wheeler 94] M. Burrows and D.J. Wheeler, "A Block-sorting Lossless Data Compression Algorithm", SRC Research Report 124, Digital Systems Res Cearch Center, Palo Alto, May 1994 gatekeeper.dec.com/pub/DEC/SRC/research-reports/SRC124.ps.Z

[Elias 75] P. Elias, "Universal Codeword Sets and Representations of the Integers", IEEE Trans. Info. Theory, Vol IT 21, No 2, pp 194-203, Mar 75

[Fenwick95] P.M. Fenwick, "Differential Ziv-Lempel Text Compression", J.UCS Vol 1, No 8 pp 587-598 Aug 1995 http://www.iicm.edu/JUCS

[Fenwick96a] P.M. Fenwick, "Block sorting text compression", Australasian Computer Science Conference, ACSC'96, Melbourne, Australia, Feb 1996. ftp.cs.auckland.ac.nz /out/peter-f/ACSC96.ps

[Fenwick 96b] P.M. Fenwick, "Block-Sorting Text Compression - Final Report", The University of Auckland, Department of Computer Science, Technical Report 130, March 1996. ftp.cs.auckland.ac.nz /out/peter-f/report130.ps

[Fenwick 96c] P.M. Fenwick, "Punctured Elias Codes for variable-length coding of the integers", The University of Auckland, Department of Computer Science Report No 137, Dec. 1996. ftp.cs.auckland.ac.nz /out/peter-f/report137.ps

[Howard and Vitter 93] Howard, P.G., Vitter, J.S., "Design and Analysis of Fast Text Compression Based on Quasi-Arithmetic Coding", Data Compression Conference, DCC-93, pp98-107.

[Lelewer and Hirschberg 91] Lelewer, D.A., Hirschberg, D.S., "Streamlining Context Models for Data Compression", Data Compression Conference, DCC-91, pp 313-322.

[Shannon 51] C.E. Shannon, "Prediction and Entropy of Printed English", Bell System Technical Journal, Vol 30, pp 50-64, Jan 1951

[Wheeler 95] D.J. Wheeler, private communication. (Oct '95) [This result was also posted to the comp.compression.research newsgroup. The files are available by anonymous FTP from ftp.cl.cam.ac.uk/users/djw3]