| Submission Procedure |
Introduction To Algorithmic Information Theory *1
Computer Science Department, University of Maine, Orono, ME 04469-5752, USA, email: markov@gandalf.umcs.maine.edu. *1 C. Calude (ed.). The Finite, the Unbounded and the Infinite, Proceedings of the Summer School "Chaitin Complexity and Applications", Mangalia, Romania, 27 June - 6 July, 1995. 1 Overview of Lectures
The following topics will be discussed in this paper. - Goals of this paper - What is AIT? - Some important pre-AIT Ideas - Fundamental Concepts of AIT - Introduction to the Logo Programming Language - The Uncomputability of H - The Hacker's Problem - The Halting Problem - Definition of Omega - The Ultimate Uncomputability of Omega - Random Strings - Some Implications of AIT - Teaching AIT 2 Goals of This Paper
The following are the goals that this paper has. - To provide a historical context for AIT. - To provide the basic concepts necessary to understand the more advanced material presented during this short course. - To provide an introduction to functional programming via the Logo programming language. - To provide examples to help understand the fundamental concepts of AIT. - To provide an overview of some key results in AIT. - To provide some insight into the delicate details that make actually make AIT work. This paper grew out of a short course on AIT that Greg Chaitin presented in June 1994, at the University of Maine. I helped with the course, and observed some of the topics that proved most difficult for students. These lectures are designed to fill-in some of the gaps in people's backgrounds that I observed in 1994. The material in these lectures is based on the work of Greg Chaitin.
Page 245 3 What is AIT?
AIT, of course, stands for Algorithmic Information Theory. The information part of the name comes from Shannon's information theory, that first proposed measuring the amount of information. The algorithmic part of the name comes from the fact that algorithms (programs) are used for measuring information content. We will discuss the basis of AIT in more detail throughout the remainder of this paper. 4 Some Important pre-AIT Ideas
This section discusses some of the important ideas that are intimately related to AIT. 4.1 The Concept of an Algorithm
A very interesting discussion of this is found in Volume 1 of Knuth's The Art of Computer Programming. After dismissing several earlier derivations, Knuth presents what he claims is the correct derivation. He notes that even as late as 1957 the word did not appear in Webster's New World Dictionary. The closest word to appear in dictionaries of that time was algorism which means the process of doing arithmetic using Arabic numerals. The word algorithm appeared as the result of confusing the word arithmetic with the name of the Persian mathematician Abu Jafar Mohammed ibn Musa al-Khowarizmi (c. 825). The word was probably first widely used for Euclid's GCD algorithm, before it came to have its present meaning of a well-defined procedure for computing something. The 1971 edition of The Compact Edition of the Oxford English Dictionary gives the following definition for algorithm: "erroneous refashioning of algorism". 4.2 The History of Entropy
Nicolas Leonard Sadi Carnot (1796-1832) was an engineer who was interested in understanding how much work can be produced by heat engines such as steam engines. He introduced many important concepts into physics (thermodynamics) including those of reversible and irreversible engine. Building upon
his work, Rudolf Clausius introduced the concept of entropy: "I
propose to name the magnitude S the entropy of the body from the Greek
word Further contributions to the field were made by Kelvin, Boltzmann and Gibbs. The last two connected entropy to statistical mechanics and showed that it can be viewed as a measure of the randomness of a collection of entities such as molecules. The work of Boltzmann and
Gibbs lead to the following expression for entropy: Page 246 4.3 Information Theory
The work of Claude Shannon showed the connection between the entropy of thermodynamics and the entropy of information theory. Many of the ideas of information theory were in the air when Claude Shannon wrote his two classic papers on information theory in 1948. Shannon showed that it made sense to measure the information content of messages and how to transmit messages correctly in the presence of noise. The importance of this work cannot be overestimated. Shannon derived the connection between the entropy of thermodynamics and the information-theoretic entropy that he used in his theory. It is interesting to note that information-theoretic entropy is the unique function on probability vectors (vectors of non-negative numbers that sum to 1) that satisfies three very simple conditions. 4.4 The Foundations of Mathematics
George Cantor did much work to develop set theory as we know it today. He also discovered the diagonal argument that laid the foundation for Gödel's work and AIT. I will give you two flavors of the diagonal argument. First, we will show that it is impossible to assign natural numbers to infinite binary sequences. On the contrary, assume that an assignment is possible that matches each natural number to some infinite string of 0s and 1s in such a way that all the natural numbers and the sequences are matched. This might be illustrated as in the following table.  Note that the sequence s = 001 ... is not in the table, if it is formed so that the i-th digit is the complement of the i-th digit in the i-th row of the table. In other words, s cannot be found in row 0, since it differs from the sequence found there in the first position. It cannot be in row 1 since it differs from the sequence found there in the second position. It cannot be in row i since it differs from the sequence found there in the i-th position. Using a similar argument, shows that it is impossible to associate the elements of a set with the set of all subsets of the set. This argument goes as follows. Assume the contrary, then there would be a bijection between elements of the set and subsets of the set. Such a bijection might be represented by the following table.  Now let Page 247 4.5 The Berry Paradox
In the Principia Mathematica, Russell and Whitehead describe an interesting paradox that lies at the bottom of AIT and provides the key insight into many of its results. To start off, first note that there are only finitely many English phrases not exceeding a certain length in words. Some of these phrases will define positive integers unambiguously. Make a list of these phrases of twenty words or less. (Alternatively, you can also limit the number of characters.) This list will define a finite set of integers, so some positive integers will not be on the list. Let Q be the smallest positive integer not on the list. Now consider the following phrase: "the smallest positive integer that cannot be defined in less than twenty words". This is a phrase of 13 words! 4.6 Undecidability
Hilbert was of the opinion that eventually algorithms would be found to solve all outstanding problems in mathematics and some of his famous problems presented at the International Mathematical Congress of 1900 tried to direct research at finding these algorithms. In 1931 Kurt Gödel published a paper showing that any system of mathematics complicated enough to include arithmetic must contain problems undecidable from the basic axioms in that system. In 1937 (a year before he got his Ph.D), Turing published the paper in which he introduced "Turing machines" and showed that the Halting Problem, deciding whether a Turing machine running on a particular input would halt or not. Turing's work is of critical importance in computer science and significantly simplified the demonstration that there are undecidable problems in formal systems. 4.7 Credit for AIT Discoveries
Three people are generally credited with co-discovering some of the basic ideas of AIT: Chaitin, Kolmogorov and Solomonoff. Solomonoff published some definitions several years before Chaitin and Kolmogorov. Chaitin has contributed the largest body of work to AIT and continues to extend the field at the present time. There is a tendency on the part of some writers to attach Kolmogorov's name to everything in the field. This makes little sense and is obviously unfair to other researchers. A curious justification for this is stated on page 84 of An Introduction to Kolmogorov Complexity and Its Applications (by Li and Vitanyi): This partly motivates our choice of associating Solomonoff's name with the universal distribution and Kolmogorov's name with algorithmic complexity, and, by extension, with the entire area. (Associating Kolmogorov's name with the complexity may also be an example of the "Matthew Effect" first noted in the Gospel according to Matthew, 25:29-30, "For to every one who has more will be given, and he will have in abundance; but from him who has not, even what he has will be taken away. And cast the worthless servant into the outer darkness; there men will weep and gnash their teeth.") Page 248 5 Some Fundamental Concepts
I will loosely define the algorithmic complexity of a string as the size of the smallest program that generates that particular string. More generally, one can define the complexity of any object as the size of the smallest program that generates it. These definitions are loose because they leave out some key details: - What language are we using? - What does generate mean? - How do we measure program size? - What exactly constitutes a program? To simplify the discussion I will fix a particular programming language (Logo) and work with it. There are a variety of clarifications needed when working with a "real" language. Note that the algorithmic complexity always exists because there are only finitely many programs having a size less than or equal to a given number. Knowing that something exists and finding it are two, sometimes, very different things. There are other sorts of complexity and even variations of Algorithmic Complexity. Since these notes are an introduction to AIT, I will just present one version of complexity. It is important to realize that the complexity of most strings cannot
be substantially shorter than the string itself. To make this
statement more precise, let's assume that we are using an alphabet
with Q letters, and that this alphabet is used for both the strings of
interest and for writing programs. Thus there are Suppose that we assume that to each "program" we
associate at most one string that it produces. It is possible that no
string is produced if the program goes into an infinite loop. Since
programs are also strings, it is easy to see that the number of
programs having length < n is bounded above by Thus at most 1/(Q - 1) of all strings of length n can be expressed by programs that are shorter. Thus, at least (Q - 2)/(Q - 1) of all strings of length n require a program of length at least n to generate. Let's use H(s) to denote the program-size complexity of s. 6 An Introduction to Logo
I will now discuss the language Logo and some of the questions that come up when dealing with trying to actually compute the complexity of a string. More specifically, I will discuss WinLogo, a public domain Logo, which comes with a very extensive help file. Logo was developed by Seymour Papert and his colleagues at MIT and Bolt, Beranek and Newman. Its purpose is to serve as a programming language that is easy enough for kids to learn, but which is, nevertheless, powerful. Logo has been mistyped as a kid's language and most people don't realize that it is actually LISP dressed up so it can be seen out on the street! Page 249 Rather than give you lots of details about Logo, I will give a very brief overview and then begin using it. Most of the terms in the language come directly from English so the language is easy to understand. BASIC was designed to provide a simple introduction to programming using numbers and to some extent strings. Logo was designed to provide a simple introduction to programming using strings and lists. There are various versions of Logo that differ slightly in the details. As stated earlier, I will base my discussion on WinLogo. Like most programming languages Logo has variables for storing data. Logo allows any variable to store any legal Logo object and to change the type of object that is stored. Logo does not require declarations of variables. All variables are global unless they are specifically declared to be local. Logo has great flexibility in what it allows as variable names. This great flexibility can cause some confusion. For example, Logo treats numbers as strings that happen to have special properties. However, you can, if you wish, use numbers as variable names! Logo is generally an interpreted language - this means that you can type individual commands and see what Logo will do. Some Logos are case-sensitive and some are not. Also, even the case sensitive Logos often are case-insensitive when dealing with the Logo primitives. Logo has a command PRINT which displays objects and does what you expect it to, except that when it prints lists it omits the outside pair of delimiters. I will illustrate and explain this soon. If you give the command PRINT 2 + 2 to the interpreter, you will get back 4 as you would expect. If X is a variable, you must use the construction :X to tell Logo that you want to reference its value. The colon (:) is necessary because a name appearing without the : is assumed to be a function. It is possible for the same string to be a function and also store a variable. If Logo spots a name around that is not quoted or preceded by :, it assumes the name represents a function call. Thus, the statement MAKE "2 3 assigns the value 3 as the value of the variable 2. When you give the command PRINT 2 + 2, the 2s are interpreted as functions that return the value 2. If you give the command you will get 6! Logo, like LISP, is a functional programming language. This means that you can string long sequences of functions together and Logo takes care of any temporary space that is needed to link the function calls. Functions can be created using the command which invokes a very primitive facility for entering the function line by line. Once a line is entered, it cannot be edited when using TO. If you give the command most Logos will invoke a more powerful editing facility, although what you get varies considerably among the implementations. For details consult the appropriate reference materials. Page 250 All Logo functions must end with the END statement. Let's look at some simple Logo functions to generate particular strings. This will get us started in Logo and also return us back to AIT. Consider the following Logo function (program): TO ANYSTRING Now simply giving Logo the command ANYSTRING will produce the indicated string. Note that unlike most programming languages, Logo only requires a single double-quote to indicate a string. Strings end when a blank has been encountered, unless the blank is to be part of the string which is indicated by using an escape character of some sort. WinLogo uses \. If you include a closing " it will be included as part of the string. ANYTHING is certainly not the shortest Logo function that can generate the indicated string. For one thing, you can pick a shorter title than ANYSTRING, such as X. Furthermore, Logo recognizes PR as an abbreviation for PRINT so we can shorten the program further. When determining program size, there are some non-obvious problems. In particular, what exactly do we count? Clearly, we need to count the letters in the function definitions, but each line in an ASCII file generally ends with two invisible characters - a carriage return and a line feed. Do we include these characters in arriving at the program size? We will soon see that Logo offers an alternative function representation, that might produce slightly different counts, so we need to decide exactly what we want to count. Using ANYSTRING, we see that for most strings, 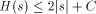 where C is a constant that depends on exactly what we count. If we count hidden characters we would get C = 27 (if I counted correctly!). You might wonder why we have Since every function begins with TO and ends with END there is little reason to include them, and in fact the WinLogo interpreter displays them for the benefit of the user, but does not include them in the representation. One needs to come to some decision about these points, but many of the choices will not affect the final results significantly. There is another important point to consider: as written above, the function ANYSTRING prints the string, but this means that no other function can use the string that is produced by ANYSTRING. We can adopt the convention that we will use printing only for illustrative or debugging purposes but that we want our functions to output the string. Logo provides an OUTPUT function that can be used for this purpose. OUTPUT can be abbreviated OP. Thus, the general string generating function can be written as: Page 251 TO X OP "ANY_STRING END If we ignore TO and the line containing END, but count the two invisible characters per line, we get that for most strings 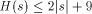 which means roughly that the length of a string is an upper bound on its program size complexity. If we include many special characters such as blanks in the string, we might need twice the length of the string + 9 as a bound if we do things the simple way. The earlier result shows that for most strings we cannot do better than the length of the string itself. LISP is notorious for the number of parentheses required by its syntax. It is sometimes claimed that LISP stands for Lots of Irritating and Stupid Parentheses. Logo works to minimize parentheses but using prefix notation and not requiring parentheses if the default number of parameters are used. For example, SUM and LIST normally take two parameters. Thus, in Logo one can write without ambiguity the following command: to produce the list 6.1 Lists in Logo
Lists in Logo are represented by using square brackets at the start and finish. Thus, [ ] represents the empty list and represents a list of 4 elements, the third of which is also a list. The convention in Logo is that if you write out a list explicitly, all strings within that list are quoted. Probably the main reason that PR does not show the outside parentheses of list is that you can give the command and just get the phrase Hello World printed. The WinLogo primitive SHOW displays a list with its outermost brackets intact. Logo has a variety of commands for manipulating lists: - FIRST LIST returns the first element of a list. Thus, FIRST [a b c] returns a. - LAST LIST returns the last element of a list. Thus, LAST [a b c] returns c. - BUTFIRST LIST (BF) returns a copy of a list consisting of everything except for the first element. Thus, BF [a b c] returns [ b c ]. - BUTLAST LIST (BL) returns a copy of a list consisting of everything except for the last element. Thus, BL [a b c] returns [a b]. Page 252 - SENTENCE LIST1 LIST2 (SE) takes two lists and returns a list which results from joining copies of the original two lists into one. Thus, SE [a b c] [a b c] returns [a b c a b c]. - FPUT ELEMENT LIST inserts the element at the beginning of a list. Thus, FPUT "a [b c] returns [a b c]. - LPUT ELEMENT LIST inserts elements at the end of a list. Thus, LPUT "c [ a b ] returns [a b c]. - ITEM NUMBER LIST returns the indicated item from the list. Thus, ITEM 2 [a b c] returns b. - COUNT OBJECT returns the "size" of a Logo object. For lists, this is the number of elements in the list. Thus, COUNT [a b c] returns 3. 6.2 String Operations in Logo
Some of the list operations apply equally well to strings. These are FIRST, LAST, BF, BL, ITEM and COUNT. ITEM can be used to select particular characters and COUNT returns the number of characters in a string. The general operator for concatenating strings together is: returns a string that is the concatenation of the two indicated strings. Thus WORD "abc "def returns abcdef. FPUT, LPUT and SE should not be used with strings. The strings "True" and "False" represent the Boolean truth values. By default, WinLogo is not casesensitive. By convention, most Logo Predicates (functions that return "True" or "False") end with the letter P. 6.3 Recursion
Much of Logo's power comes from its ready facility with recursion and the fact that both strings and lists are recursive data types. For people unfamiliar with recursion, I should note that the basic form of a recursive program is if Base-Case [Do Some Direct Calculation] Reduce Complex Cases to Simpler Cases In Logo you can use the constructions IF CONDITION [Instructions] or IFELSE COND [Inst1][Inst2] Long lines may be continued by using~at the end of the line. 6.4 Church's Thesis
All our results are stated using Logo so they might be accessible to as wide an audience as possible. The reader should note that Church's Thesis, a principle which I will paraphrase as "anything that can be computed using one computer language can be computed using any other computer language". Thus, we can draw universal conclusions even though we are using Logo to achieve our results. Page 253 6.5 The Size of a Logo Program
Now let's consider how to compute the size of a Logo function (program). Logo has the function TEXT F-Name that gives the representation of the function F-Name. For Example, TEXT "X where X is as above returns the following: (I have added some extra spaces to make the result easier to read). Note that TO and END are missing. The first empty list is a list of the parameters (when present, these appear without the : even though they appear with a colon in the original definition). You can't immediately apply COUNT to TEXT, because that would only tell you how many lines you have and not how many characters. Let's look at a complete function that calculates function size. The following two functions provide the muscle needed to compute the size of a "program". Notice how we have written the functions separately for easier comprehension. TO PROGSIZE :PROG OP SUM COUNT :PROG SIZE TEXT :PROG END PROGSIZE basically just adds the length of the name to the number returned by SIZE, which is described below. Note how the input parameter is indicated by :prog. TO SIZE :OBJ IF NOT LISTP :OBJ [OP COUNT :OBJ] IF EMPTYP :OBJ [OP 2] IF 1=COUNT :OBJ [OP 2 + SIZE FIRST :OBJ] OP (SUM 1 SIZE FIRST :OBJ SIZE BF :OBJ) END SIZE illustrates many aspects of Logo programming. Built-in Logo predicates generally end in P. Thus, LISTP OBJECT tells if OBJECT is a list, while EMPTYP OBJECT tells if OBJECT is empty (either string or list). Logo also provides some infix operators such as =, +, *, -, but you will sometimes have problems with these. If you do, use the Logo prefix operators EQUALP, SUM, PRODUCT, DIFFERENCE, etc. SIZE works as follows. If the object is not a list (we are ignoring the possibility that the object can be an array because most Logos don't have arrays), COUNT returns its size. Note that once OP is invoked, the function returns a value and that particular call ceases so you can often use IFs rather than IFELSEs. If we get past the first line, we must be dealing with a list. The next line checks whether it is the empty list. If it is, the empty list it has a size of 2 because it consists just of two brackets. The next case considered is a list of just a single item. Here the size is just 2 + the size of the item, since a pair of brackets is added to the item. The last case considered is that of a list with several items. Here we must allow for the single blank that is put between every pair of objects. The fact that Logo encourages users to break their work into separate function definitions now complicates our attempt to produce a program-size measure. Page 254 Since functions can call other functions, just measuring the size of the calling function need not give a true measure of its complexity since much of its functionality might be buried inside another function. For example, PROGSIZE has most of its complexity buried in SIZE so simply asking for PROGSIZE "PROGSIZE will give a misleading result. What we are aiming at is to define the program size as the size of the master program and all its subprograms together with any data that is defined. This is complicated by a feature that we now discuss. WinLogo and most other Logos use a workspace which stores function definitions, global variable definitions and other information. Any Logo function can access any of this information, so you must be careful when you measure program size. If you use functions not defined in the workspace, WinLogo automatically searches in various places for the definition (the details are in the extensive online help that comes with WinLogo). Thus, if you are not careful you can be invoking much Logo code by a function that is quite short. There are at least two ways to get around these various problems and get a measure of the complexity size. One way, is to pick a suitably "clean" computer with no hidden Logo definitions, identify which function in the workspace produces the result and then measure the workspace in bytes. This solution is simple to understand, but unfortunately it forces us out of Logo and into the domain of the operating system. Ideally, we could do all of this work in Logo. I will now describe how to do this. We have seen how the TEXT command returns the body of a function. The command goes from the representation of a function to its definition. BODY should have the same format as produced by TEXT. Below we show how to rewrite PROGSIZE so it is completely contained. TO PROGSIZEX :FUN DEFINE "SIZEX [[OBJ] ~ [ IF NOT LISTP :OBJ [OP COUNT :OBJ]] ~ [IF EMPTYP :OBJ [OP 2]] ~ [IF 1=COUNT :OBJ [OP 2 + SIZE FIRST :OBJ]] ~ [OP (SUM 1 SIZE FIRST :OBJ SIZE BF :OBJ)]] OP SUM COUNT :FUN SIZEX TEXT :FUN END Recall, that the character~ is used to continue a line. 6.6 A More Formal Definition of H
We are now ready to more formally define what we mean by H(s) where s is a string or any other Logo object for that matter. We first create a workspace on a computer that does not have access to any other Logo workspaces. Furthermore, the workspace we work in must contain only one function which has no input parameters, so that all input has to be included in the function. Page 255 If any additional functions need to be defined, this must be done as indicated above by PROGSIZEX in the body of the lone function. When this lone function executes, it produces the desired object s. To actually measure the function correctly we must measure it before it runs since running the function can introduce new functions and variables as well as erase functions and variables. I stress these points so you can better appreciate Greg Chaitin's "Toy" LISP - it will clarify why he needs to do things in a certain way. I should note that WinLogo does not always perform correctly when you define functions in the body of a function, in particular you sometimes have to run the function twice for it to work correctly. I will ignore this little problem and assume that it all works well enough for our purposes. 6.7 Some Examples
Now that we have discussed some of the fine points of measurement, we can write our functions in a more relaxed style knowing that we can always cram everything together into one bundle if necessary for measurement. Consider the following function: TO P2 :STR IF EMPTYP :STR [OP "X] LOCAL "J MAKE "J P2 BF :STR OP WORD :J :J END If you input a string of length N , you get a
string of TO PQ OP P2 P2 P2 "Y END PQ will output a string of 16 Xs. It is
clear that if we add additional instances of P2 and a blank on the
second line of PQ we get an super-exponentially increasing sequence
of strings. In other words, we would get strings of length Notice that adding an extra P2 just increases the size of the program by 3, but the size of the output monstrously. These simple examples show that some extremely long strings have small H. The following shows how we could create a self-contained function that behaves like PQ - in the future I will display functions using the more relaxed syntax only. TO PQX DEFINE "P2X ~ [[STR] ~ [IF EMPTYP :STR [OP "X]] ~ [LOCAL "J] ~ [MAKE "J P2X BF :STR] ~ Page 256 [OP WORD :J :J]] OP P2X P2X P2X "Y END 7 Actually Measuring String Complexity
I hope that the preceding discussion has given you some insight into actually measuring H for various strings. By now, you are probably chaffing at the bit and ready to start computing some values of H. Unfortunately, I will now illustrate why this is more difficult that might appear. It turns out that it is impossible to compute H for more than a finite number of strings! 7.1 The Uncomputability of H
An argument based on the Berry Paradox shows quite convincingly that H is not computable for an infinite number of strings. Assume that we have a fixed length function, called H, that correctly computes the complexity of infinitely many strings. Since there are only finitely many programs less than a certain length, any infinite collection of strings must contain strings of arbitrarily large complexity. Thus, going through all possible strings ensures that we will eventually find strings of arbitrarily large complexity. The basic idea of this proof is expressed by the following Logo functions. In particular, the person claiming that H is computable must supply a way to compute H. We will show that the proposed solution for H cannot be correct without examining the inner structure of H. Theorem: No Logo function can correctly compute H for all strings. Proof: Consider the following Logo functions. TO FOOL OP EXPLORE " END TO EXPLORE :STR IF NOT LESSP H :STR :N [OP :STR] OP EXPLORE NEXT :STR END TO H :STR ; WinLogo comments begin with a ; ; H supposedly calculates H(str) ; This has the appropriate code. END TO NEXT :STR ; assume only ASCII chars 33..90 ; NEXT returns the "next" string IF EMPTYP :STR [OP CHAR 33] IF 90 ? ASCII LAST :STR~ Page 257 [OP WORD BL :STR CHAR 1+ASCII LAST :STR] OP WORD NEXT BL :STR CHAR 33 END TO BASE :STR ;returns a string of !s of same length as :str IF EMPTYP :STR [OP " ] OP WORD CHAR 33 BASE BF :STR END Note that the above program will generate a string of complexity greater than N. The only problem we have here is that the program has size 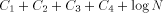 where Yet by definition, a string of complexity N or greater, can only be generated by a program of size at least N . Clearly, 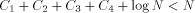 for N arbitrarily large,
which contradicts the definition of complexity N. You can run the above program and get a concrete realization of the Berry Paradox, which you will see again later in this paper. Logo has a RUN command that attempts to run a list of instructions. You can feed anything to RUN and it might halt with an error message. The following illustrates how you can put the definition of a program and its execution into a single list. Thus, outputs the string hello world. (\ includes a blank in the string). This approach is somewhat more elegant than the one we have been using earlier because it includes the execution of the function along with the definition. I will refer to expressions of the form above as functional expressions. In other words, a functional expression is a Logo list that produces something (maybe an error message) when executed with the RUN command. We can now define the complexity of a string as the size of the smallest functional expression that can produce the string. Note that it is easy to go from standard function definitions to functional expressions. Unfortunately, WinLogo does not always correctly run the functional expression the first time. Page 258 Note that the size of the functional expression can vary significantly from the size of the function definition because it might include an extra copy of the function's name, which could be arbitrarily long. 9 Properties of H
As we have seen, H is not computable. Nevertheless we can derive some of its properties. The following is an example of this. 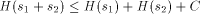 where + between strings indicates concatenation. I will now give the proof of this, which is straightforward. Let In this case, C = 16 ( 2 for extra brackets, 4 for WORD, 6 for the two RUNs, 4 for the blanks). 10 More on Functional Expressions
For the "hello world" example concatenated to itself we would have that E looks like the following: [word run [ define "hw [ [ [op "hello\ world ] ] hw] run [ define "hw [ [ [op "hello\ world ] ] hw] The difficulty of reading functional expressions explains why I stress the less formal, conventional description of programs. It is important to understand how functional expressions can be constructed from more conventional programs and how they operate. 11 Converting Lists to Strings
It is easy to write a Logo function, List2String that will convert Logo lists to strings. List2String can be based on the SIZE function described above. Writing such a function is left to you as an exercise (see the exercise section). Thus, any function can be converted into a string by using TEXT to create its list representation and then using List2String to create the string representation. One can also write a string parsing function that will convert strings into lists where this make sense. You might expect this to be quite a bit more complicated than List2String. WinLogo has a command called PARSE that converts strings into lists. Unfortunately, the version PARSE that I have does not permit embedding blanks into strings since it uses them as separators. You can get around this by creating a function that concatenates strings together with a blank between them or you can write a different parser as an exercise. I will just use - to represent embedded blanks in the following example. Consider the following sequence of instructions: which produce the string hello-world as an output. Page 259 make "x "define" "hw" "["["]"[op" "hello-world"]"]hw make "xp parse :x run :xp Note how the backslash (\) needs to be used to include characters such as brackets in the string. Each new refinement makes the functions less readable, so I will continue to work with the standard programming notation. The important thing is to note that we can move from strings to lists and lists to strings. 12 The Hacker's Problem
Closely related to the problem of computing H is the Hacker's Problem: how can you show that a given program is the shortest program that can generate a particular result? Greg Chaitin refers to such programs as elegant programs. My name for the problem comes from the book Hackers by Stephen Levy which details how many hackers were on an endless quest to find the shortest program to accomplish some task. The hackers were never able to prove that some program was the shortest. We will now see why this is no accident. Greg Chaitin participated in such a quest when he was learning programming while in high school. In view of the uncomputability of H, you might suspect that the Hacker's Problem is also not solvable. We will now see how to apply essentially the Berry Paradox argument to this problem. Usually, when people talk about proving something they imply that one must use an axiomatic system of some type. The same object can be achieved by thinking of an axiomatic system as a computer program that can correctly decide a certain question. You will soon see that it is impossible for a any program to correctly decide for infinitely many programs that they are minimal programs. Furthermore, the complexity of the algorithmic system bounds the complexity of the programs for which minimality can be demonstrated. Thus, the checking program cannot correctly decide whether programs sufficiently larger than itself are minimal! Theorem: The Hacker's Problem cannot be solved in general, i.e., there are only finitely many provably elegant programs. Proof: Suppose that there was a Logo function that could correctly analyze functional expressions given as strings and decide correctly whether or not they were minimal. Consider the following Logo routines. TO FOOL OP EXPLORE " END TO EXPLORE :STR IF NOT LEGALFEP :STR [OP EXPLORE NEXT :STR] IF LESSP COUNT :STR :N [OP EXPLORE NEXT :STR] IF NOT ELEGANTP :STR [OP EXPLORE NEXT :STR] OP RUN PARSE :STR END Page 260 TO LEGALFEP :STR ;TELLS IF :STR IS A LEGAL ;FUNCTIONAL EXPRESSION END TO ELEGANTP :STR ;SUPPOSEDLY TELLS IF :STR IS ELEGANT OP "TRUE END The size of the program above is 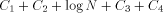 where ELEGANTP represents the elegance detector which we are assuming exists. LEGALFEP is a function that can be built which determines whether a given string can be made into a legal functional expression. For compiled languages, the compiler is the arbiter who decides whether the input is a legal program for a particular language. Interpreted languages tend not to have comprehensive syntax checking as a feature, but there is no reason why it can't be done. Of course, this is not a trivial task. I will assume that such a program can be written for Logo. PARSE is used to represent a function that converts strings to functional expressions when possible. It can be replaced by something more accurate. Thus, we have for all N; 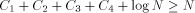 which is impossible. We can draw some additional information from this argument. In particular, we have that 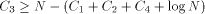 Recall that 13 The Halting Problem
I will now show how our inability to compute H(s) or to solve the Hacker's Problem implies that the Halting Problem (telling whether a given program will halt) is not solvable. In both cases, the argument is almost the same. First, let's show that if the Halting Problem is solvable by a computer program, we could construct a computer program (an extremely slow one) that could compute H(s). Page 261 We proceed as in the Hacker's Problem and begin going through all the "programs", by which I mean all functional expressions with no input parameters. If we could tell which ones will halt and which ones won't, we just discard the ones that don't halt and run the ones that will halt and collect the results. We create a list of all "program" outputs arranged by size of the functional expressions. Now to compute H(s) just read through the list until you first spot s. It has to appear at least once, and its first appearance is with the shortest program that generates it. Since we can't compute H(s); it follows that it is impossible to solve the Halting Problem. We don't really need to construct the list of all programs, since we can examine outputs "on the fly" and compare them to s: The following Logo code shows how this can be done. TO H :STR OP COUNT EXPLORE :STR " END TO EXPLORE :STR :PRG IF NOT LEGALFEP :PRG [OP EXPLORE :STR NEXT :PRG] IF NOT HALTP :PRG [OP EXPLORE :STR NEXT :PRG] IF NOT EQUALP :STR RUN PARSE :PRG [OP EXPLORE :STR NEXT :PRG] OP :PRG END TO HALTP :PRG ; TELLS IF PROGRAM REPRESENTED ; BY THE STRING :PRG WILL HALT END Note that we use the NEXT and LEGALFEP functions that we discussed earlier. Of course, HALTP is our hypothetical solution to the Halting Problem. The argument based on the Hacker's Problem is similar: by eliminating the programs that never halt we can construct a list of all possible outputs that match up with program size. We also check our candidate program to make sure that it halts and produces an output. Once such a list is constructed we can decide whether a program is elegant by simply checking all entries that come earlier in the list - if we find the same output earlier, we see whether the corresponding program is strictly shorter. If it is, then the program being tested is not elegant. If it is the same length we continue our search until we have examined all earlier entries. Another proof that shows that the ability to solve the Halting Problem allows us to solve the Hacker's Problem, proceeds as follows. If we can solve the Halting Problem we could compute H as shown earlier. If we can compute H, we can solve the Hacker's Problem using the following Logo code which uses some of the Logo functions discussed earlier. TO ELEGANTP :PRG IF NOT LEGALFEP :PRG [OP "FALSE] IF NOT HALTP :PRG [OP "FALSE] Page 262 LOCAL "X MAKE "X RUN PARSE :PRG IF LESSP H :X COUNT :PRG [OP "FALSE] OP "TRUE END Reference [5] contains two proofs that show that being able to compute program-size complexity would confer the ability to solve the Halting Problem. 14 Chaitin's |
|||||||||||||||||
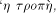 , a transformation. I have intentionally formed the
word entropy so as to be as similar as possible to the word energy,
since both these quantities, which are to be known by these names, as
so nearly related to each other in their physical significance that a
certain similarity in their names seemed to me advantageous ..."
, a transformation. I have intentionally formed the
word entropy so as to be as similar as possible to the word energy,
since both these quantities, which are to be known by these names, as
so nearly related to each other in their physical significance that a
certain similarity in their names seemed to me advantageous ..."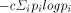 where c is some constant > 0 and the
where c is some constant > 0 and the 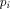 are probabilities of various states.
are probabilities of various states.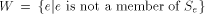 . Note that W cannot be in the
listing. If it were, we would have
. Note that W cannot be in the
listing. If it were, we would have 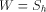 for some element h in the
set. If h were in W, then h would be in
for some element h in the
set. If h were in W, then h would be in 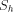 , but W is exactly the set
of elements such e is not in
, but W is exactly the set
of elements such e is not in 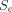 . If h were not in W, then h would
not be in
. If h were not in W, then h would
not be in 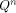 strings of
length n.
strings of
length n.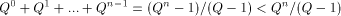
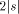 , where
, where 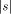 is the
length of s, rather than just
is the
length of s, rather than just 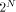 Xs as output. Now consider the following Logo function.
Xs as output. Now consider the following Logo function.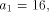
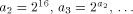 It quickly gets beyond the capability of
real computers to produce strings of the appropriate length. By using
the Ackermann function, one can generate "really large strings."
It quickly gets beyond the capability of
real computers to produce strings of the appropriate length. By using
the Ackermann function, one can generate "really large strings." is the size of FOOL,
is the size of FOOL,  is the size of
EXPLORE, ,
is the size of
EXPLORE, , 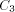 is the size of H, and
is the size of H, and 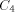 is the size of NEXT and
BASE. Note that we need log N included in the size of EXPLORE since as
we pick arbitrarily large N the size of EXPLORE will grow
logarithmically. We use abstract constants to denote the sizes of the
routines, since it is their sizes in the coded form (see the next
section) that really count rather than their sizes in the expanded
form listed above.
is the size of NEXT and
BASE. Note that we need log N included in the size of EXPLORE since as
we pick arbitrarily large N the size of EXPLORE will grow
logarithmically. We use abstract constants to denote the sizes of the
routines, since it is their sizes in the coded form (see the next
section) that really count rather than their sizes in the expanded
form listed above.
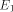 be a functional expression that
evaluates to
be a functional expression that
evaluates to 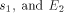 a functional expression that evaluates to
a functional expression that evaluates to 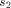 , then let E be the functional expression:
, then let E be the functional expression: 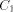 is the size of FOOL,
is the size of FOOL, 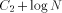 is the size of EXPLORE,
is the size of EXPLORE, 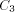 is the
size of LEGALFEP and ELEGANTP, and
is the
size of LEGALFEP and ELEGANTP, and 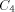 is the size of NEXT and BASE
(which were used earlier). FOOL, however, produces strings of
complexity N; where N is arbitrary.
is the size of NEXT and BASE
(which were used earlier). FOOL, however, produces strings of
complexity N; where N is arbitrary.
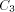 included the size of the
elegance-recognition program. The conclusion here is that any program
that can prove that a program of size N is elegant, essentially must
have size at least N itself. Thus, programs cannot prove the elegance
of programs that are substantially larger than they are themselves.
included the size of the
elegance-recognition program. The conclusion here is that any program
that can prove that a program of size N is elegant, essentially must
have size at least N itself. Thus, programs cannot prove the elegance
of programs that are substantially larger than they are themselves.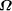
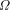 ). The bits
of
). The bits
of 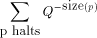
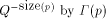 , and the sum of
, and the sum of 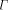 over a set, S; by
over a set, S; by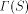 . An important consideration is whether the above definition
for
. An important consideration is whether the above definition
for 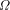 makes sense, i.e., does the sum converge to a value between
0 and 1.
makes sense, i.e., does the sum converge to a value between
0 and 1.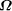
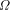 is bound up with knowing which programs halt it
should not be surprising to learn that
is bound up with knowing which programs halt it
should not be surprising to learn that 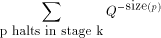
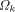 .
.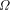 in the
first n digits, and will only be smaller in digits
that come after these n digits.
in the
first n digits, and will only be smaller in digits
that come after these n digits.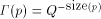 would alter the first digits
of
would alter the first digits
of 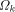 and hence
and hence 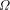 . Since we are assuming that we know the
first n bits of
. Since we are assuming that we know the
first n bits of 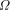 exceed or equal the given value and
returns a list of the functional expressions that halted in the search
to this point.
exceed or equal the given value and
returns a list of the functional expressions that halted in the search
to this point. 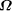
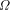 exists. The
key idea is based on the Kraft inequality which says that the sum of
the weights of the elements of any prefix-set of strings is bounded
above by 1. The weight of a string, s, is given by
exists. The
key idea is based on the Kraft inequality which says that the sum of
the weights of the elements of any prefix-set of strings is bounded
above by 1. The weight of a string, s, is given by 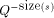 where Q is the number of elements in the alphabet.
where Q is the number of elements in the alphabet.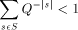
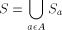
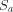 consists of all elements
of S that begin with the letter a (note
consists of all elements
of S that begin with the letter a (note 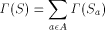
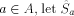 be the set of strings formed
by removing the first element of each element in
be the set of strings formed
by removing the first element of each element in 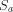 . Observe that
. Observe that
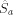 a must be prefix-free, otherwise
a must be prefix-free, otherwise 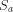 would not be
prefix-free. Note further that
would not be
prefix-free. Note further that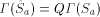
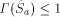
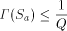
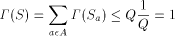

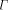 would exceed 1, but this is
impossible. Thus, the
would exceed 1, but this is
impossible. Thus, the 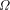 exists!
exists!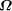
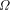 is unknowable. Chaitin has discussed this in depth
and has extended these results in many different directions. I cannot
develop this theory in detail here, but will summarize some of the key
results.
is unknowable. Chaitin has discussed this in depth
and has extended these results in many different directions. I cannot
develop this theory in detail here, but will summarize some of the key
results.