ALGORITHMIC INFORMATION THEORY: OPEN PROBLEMS *1
Cristian Calude (Computer Science Department, The University of Auckland, Private Bag
92019, Auckland, New Zealand)
cristian@cs.auckland.ac.nz.
Abstract:
This
note collects some open problems in AIT which have been discussed
during the Summer School ``Chaitin Complexity and Applications''. Each
problem comes with the name(s) of the person(s) who suggested it, and
more details about the listed open problems can be found directly by
contacting the correspondent author:
G. J. Chaitin (email:
chaitin@watson.ibm.com)
, F. Geurts (email:
gf@info.ucl.ac.be)
, H. Jürgensen
(email:
helmut@uwo.ca)
, T. Odor (email:
odor@math-inst.hu)
, K. Svozil
(email:
svozil@tph.tuwien.ac.at)
.
This
list will be periodically up-to-dated in the home-page of the CDMTCS
at url
http://www.cs.auckland.ac.nz/CDMTCS/researchreports/ait.openproblems.ps.gz
1. Find questions in algebra, topology and geometry that are
equivalent to determining bits of 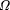 . (G. J. Chaitin) . (G. J. Chaitin) 2. What is
an interesting or natural mathematical question? (G. J. Chaitin) 3. How often is such a question independent of the usual axioms? (I
suspect the answer is ``Quite often!'') (G. J. Chaitin) 4. Show that a
classical open question in number theory, such as the Riemann
hypothesis, is independent of the usual axioms. (I suspect that this
is often the case, but that it cannot be proven.) (G. J. Chaitin) 5. The non-trivial zeros of Riemann's Zeta function are uniformly
distributed, i.e. if we denote them by
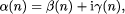 then for every positive 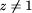 , the sequence , the sequence
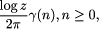 is uniformly distributed modulo 1. Do non-trivial zeros of Riemann's Zeta
function form a random sequence? (C. Calude) 6. When doing
mathematics, should we take incompleteness seriously or is it a red
herring? (I believe that we should take incompleteness very seriously
indeed.) (G. J. Chaitin) 7. Is mathematics quasi-empirical? In other
words, should mathematics be done more like physics is done? (I
believe the answer to both questions is ``Yes.'') (G. J. Chaitin) _________________ *1 C. Calude (ed.). The Finite, the Unbounded and the Infinite,
Proceedings of the Summer School ``Chaitin Complexity and
Applications'', Mangalia, Romania, 27 June -- 6 July, 1995. Page 439
8. Further develop the theory of program-size complexity for infinite
computations. Particularly, study the relations between program-size
complexity and algorithmic probability. (G. J. Chaitin) 9. Chaitin
complexity has been defined for finite strings. It would be
interesting to extend it to infinite strings. Two ways can be
envisaged: -- (a) using non-terminating programs, looping forever, and
generating infinite strings in an infinite amount of time; -- (b) using computational models dealing with infinite strings in finite amounts of time (cellular automata, functions on reals,
etc.). (F. Geurts) The first part has already received a small
attention. The second one is probably another way to think about this complexity. (F. Geurts) 10. Is it possible to describe the
``deterministic chaos'' by means of Chaitin complexity? Discrete-time
dynamical systems are called ``chaotic'' if they are sensitive to
initial conditions. What is the relation between this definition
(using topological transitivity and density of periodic points) and
Chaitin complexity? (F. Geurts) 11. Study the transformations that
preserve random strings and sequences. (C. Calude, H. Jürgensen) 12. Further develop algorithmic information theory for bi-infinite
sequences and, more generally, for constructive cpo's. (C. Calude,
H. Jürgensen) An idea would be to use bi-infinite cellular automata
as computational models. (F. Geurts) 13. Every Chaitin random string
is Kolmogorov random, but the converse is not true. Identify natural
properties associated to ``randomness'' which are satisfied by Chaitin
random strings, but not by Kolmogorov random strings. (C. Calude) 14. In a topological sense, ``many'' Kolmogorov random strings are not
Chaitin random. Prove Solovay's Conjecture: There exists a constant L
such that for all sufficiently large n, there are at least 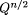 strings of length n; s, such that
strings of length n; s, such that 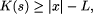 and and
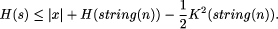 (Here Q is the size
of the underlying alphabet, H and K are, respectively, Chaitin and
Kolmogorov-Chaitin complexities, cf. C. Calude, Information and
Randomness, Springer, 1994.) 15. Axiomatize algorithmic information theory. (H. Jürgensen) 16. Constructive mathematics is essentially
mathematics plus the assumption that ``existence =
computability''. Constructions and objects in constructive mathematics
have been studied from the point of view of dynamic complexities and
it would be interesting to study them also from the point of view of
program-size complexity. (C. Calude) 17. Derive incompleteness results
for the determination of quantum algorithmic information. (K. Svozil) 18. Is there any model of computation in which the Invariance Theorem
holds true also for the time complexity? (C. Calude) 19. Define and
study the symmetry of random strings and sequences. Is the absence of
symmetry a symptom of non-randomness? (C. Calude) 20. Study binary
operations which preserve random strings/sequences. (T. Odor) Page 440
21. Compute as many as possible bits of 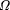 . A possible way would
be to run through all ``meaningful'', not all, programs. (C. Calude) . A possible way would
be to run through all ``meaningful'', not all, programs. (C. Calude) 22. The degree of randomness of a string x depends upon the complexity
of the string x compared with the complexities of all strings having
the same length. Extend this definition of randomness ``with respect
to an arbitrary finite set''. An appropriate solution should conform
the following intuitive fact: if a finite set of strings M containing
m elements, where m is very large, can be defined by a program of
length negligible when compared with log m, then almost all elements
of M should have maximal complexity (which is close to log m); these
strings should be ``random'' with respect to M . (C. Calude) Page 441
|