Conditional Branching is not Necessary for Universal Computation in von Neumann Computers

Abstract: In this paper we discuss the issue of the minimal instruction set necessary for universal computation. Our computing model is a machine consisting of a processor with a single n-bit register and a separate memory of n-bit words. We show that four simple instructions are sufficient in order to evaluate any computable function. Such reduction of the instruction set can only be achieved by exploiting the properties of self-modifying programs. Then we prove that, surprisingly, conditional branching can be substituted by unconditional branching. This is the main result of this paper. Therefore any computable function can be computed using only the instructions LOAD, STORE, INC and GOTO (unconditional branching). We also show that externally stored looping programs using indirect addressing and no branches are as powerful as conventional computer programs.

Categories: F.1.1, Models of Computation, Self-Modifying Machines, C.1 Processor Architectures.

1 The Computing Model

In theoretical computer science several different computability paradigms have been developed which lead to the definition of exactly the same set of computable functions. The usual approach is to postulate a general information processing model with a minimal incarnation. Turing machines, for example, are finite automata with a moving read-write head, an unbounded storage tape and simple state transition rules. They transform a single bit at each time step, yet they can compute anything that general recursive functions, lambda calculus or Post rewriting systems can. Computers with a von Neumann architecture are just another alternative for the solution of the computability problem. Provided they have enough memory, they are as powerful as Turing machines, that is random access machines are capable of universal computation (e.g. [Papadimitriou 94]).

All this is well-known and in some cases there has been an on-going contest to find the minimal device still capable of universal computation. There are universal Turing machines with just a few states and two symbols [Minsky 67]. One-dimensional cellular automata with two symbols and a small neighborhood are also universal (e.g. [Wolfram 86]). However, much less thought has been given to the question of finding the minimal von Neumann computer still capable of universal computation. A notable exception is Minsky, who proves that a machine with a single integer register (unbounded in its numerical capacity) and capable of executing multiplication and conditional division is still a universal computer because it can simulate any Turing machine [Minsky 67]. Two unbounded registers and some simple assembler instructions led also to a universal computer [Minsky 67].

Minsky's approach is pervasive and the minimal architecture he defines seems to be the best we can do with a single register. Yet there is something artificial in this assumption, because the spirit of a Turing machine is to use a small processor (the read-write head with a finite number of states) and an unbounded amount of passive memory. An infinite register leads to an infinite processor. We would like to improve Minsky's results in the sense that the processor must be of finite size although the memory can have an unbounded size, just like in a Turing machine. The instruction set we will use is also simpler than Minsky's. Our instruction set exploits the properties of modular arithmetic, the one implemented by registers of finite size in von Neumann machines.

Patterson and Hennessy mention that a single instruction can emulate all others in a universal computer [Patterson, Hennessy 94]. The instruction subtracts two numbers stored at two specified addresses, stores the result back and jumps to a given address if the result is negative. If the result is positive the next instruction in the sequence is executed. However, this single instruction is too high-powered because it is actually a mixture of elementary instructions. It contains everything: loads, stores, subtraction and conditional branching. This single instruction is actually of a more high-level type than the minimal instruction set we discuss below.

So called transport-triggered architectures [Corporaal 92] provide a single instruction for the compiler, i.e. the MOVE instruction. The computer consists of several arithmetical units, conditional units and I/O devices. The registers of the units are memory mapped and an operation is triggered by a MOVE operation [Jones 88]. Loading two numbers in the addition unit, for example, triggers an addition and the result can be put into memory using another MOVE. However, from a logical point of view, such architectures work with a large set of hardware implemented operations (addition, subtraction, numerical tests for conditional branching, etc.), each triggered by a MOVE operation to a specific address. Obviously these machines are using more than one instruction, but this simple fact is masked to the compiler which only schedules MOVE instructions. Of course, the programmer is aware that he is using a much larger implicit instruction set. Therefore these machines are not comparable to the minimal architecture that we discuss in this paper.

Another motivation to look for a minimal computer architecture has to do with the history of computers. Between 1936 and 1945 different electronic and mechanical computing devices were built in the USA and Europe. A natural question to ask is which one of them qualifies as the first genuine universal computer. In some books on the histiry of computing the dividing line between calculating machines and universal computers is drawn by considering whether the program is externally stored or is kept in memory. As we will see, the stored program concept is important but only if complemented by the right set of logical instructions. This paper improves Minsky's results by showing that self-modifying programs and four elementary instructions (which do not include conditional jump!) are all that is needed for universal computation in von Neumann machines.

Our computing model is the following: the processor contains a single n-bit register (called the accumulator) and an external memory with n bits per word.

The instruction set consist of the following five instructions

LOAD A   ; load address A into accumulator
STORE A  ; store accumulator into address A
CLR      ; clear accumulator
INC      ; increment accumulator
BRZ X    ; branch to address X if accumulator is zero

The instructions have an opcode and an address field. The program is stored in memory and is executed sequentially, instruction by instruction, until a conditional branch is taken. In this case execution continues at the new address defined by the branch.

We do not deal with the problem of extracting the result of the computation from the machine (since some kind of output instruction is needed). We assume that the input for a computation can be loaded into memory and read off after the machine halts. Therefore we do not consider input, output or halt instructions. This is the usual convention when dealing with Turing machines.

2 Additional Instructions

Some simple examples should convince the reader that the above set of instructions is all we need to implement any computation (when enough memory is available). We will define some macros, that is, sequences of instructions represented by a mnemonic and containing arguments. In the following we assume that addresses are represented by alphanumerical labels. Those beginning with upper case denote data or reserved memory cells. The absolute address is encoded in the address field of the instruction. The example below is the definition of the instruction CLR A, which sets memory address A to zero:

CLR A |CLR
        |STORE A

A similar definition can be used to define the instruction INC A which increments the contents of address A. The instruction MOV A,B copies the contents of address A to address B.

MOV A, B |LOAD A
           |STORE B

The instruction below jumps to address X if address A contains zero:

BRZ A, X |LOAD A
           |BRZ X

The unconditional jump can be defined as follows:

GOTO X |CLR
         |BRZ X

The void instruction is sometimes useful when we need a place filler:

NOP|STORE T0

Some addresses must be reserved for temporary computations or to store constants. They are denoted by T0, T1, etc. Note that each macro should use different temporary memory cells in order to avoid interferences. The labels of addresses are assumed to be local to the macro definition. The macro processor or the programmer must take care of transforming them into the right absolute addresses.

The instruction below produces the binary complement of the contents of address A. It works by incrementing A until it becomes zero. Since the accumulator is only n bits long it holds that A+CMPL(A)+1=0.

CMPL A |     CLR T1
         |loop:INC A
         |     BRZ A, end
         |     INC T1
         |     GOTO loop
         |end: MOV T1, A

Using the macro for complementing it is now easy to negate a number stored in address A:

NEG A |CMPL A
        |INC A

The decrement instruction can be written now as:

DEC A |NEG A
        |INC A
        |NEG A

Note that we are making no special effort to be "efficient", that is, to minimize the number of computer cycles. All we want is to show that all relevant computations can be performed with this minimal machine. The addition B:=A+B, for example, can be programmed as follows:

ADD A, B |loop: BRZ A, end
           |INC B
           |DEC A
           |GOTO loop
           |end: NOP

It is very useful to have shifts when dealing with multiplication and division. A left shift can be implemented by adding a number to itself. A shift to the right is somewhat more complicated. The code below decrements the argument two times for each increment to the temporary variable T3 (initially set to zero). The result is a division of the argument A by 2.

SHR A |     CLR T3
        |loop:BRZ A, end
        |     DEC A
        |     BRZ A, end
        |     DEC A
        |     INC T3
        |     GOTO loop
        |end: MOV T3, A

These examples should convince the reader that any interesting arithmetical operation can be performed with this machine. Care must be taken not to call macros recursively and not to overwrite temporary variables, but this is a minor technical point for the programmer.

3 Self-Modifying Programs

The machine defined above can compute sequences of arithmetical operations, yet we are still not satisfied. There is still a problem if we want to add a list of numbers or copy a block of memory from one location to the other. Indirect addressing could solve this problem, but we did not include this feature in the original design. Therefore the only other alternative is to write self-modifying programs, that is, portions of code that generate the absolute addresses needed.

An example can illustrate the general idea. Assume that we want to define a new instruction LOAD (A) that loads into the accumulator the contents of the memory cell whose address is stored in A. The appropriate code is the following:

LOAD (A) |      MOV "LOAD", T4
           |      ADD A, T4
           |      MOV T4, inst
           |inst: 0 ; a zero acts as place filler

The macro MOV "LOAD",T4 means that the opcode of the load operation has been stored (as part of the program) at a temporary address T4 which is now being referenced in order to load this opcode into T4. Once this has been done the instruction "LOAD address contained in A" is created by adding A to the opcode. The result is stored at address "inst", just before the instruction in this address is executed. Therefore, the load instruction is constructed first and then it is executed. In a similar way we can define the instruction STORE (A), that is, the store instruction with indirect addressing.

The instruction below copies one block of memory of N words starting at the address contained in A to the memory cells starting at the address contained in B. The expanded code contains two memory cells which are being modified in each cycle of the loop.

COPY A, B, N |loop: BRZ N, end
               |      DEC N
               |      LOAD (A)
               |      STORE (B)
               |      INC A
               |      INC B
               |      GOTO loop
               |end:  NOP

The instruction set we defined at the beginning is universal because we can implement a simulation of any Turing machine. The code for the simulator can be written using the primitive instructions and the tape can be simulated by a contiguous region of memory which can be referenced using a pointer (indirect addressing). Note that since Turing machines with a tape infinite in only one direction are equivalent to the standard ones, we do not have any problem

by restricting the simulated tape to extend in only one direction in memory [Minsky 67].

We can even drop one instruction: CLR is unnecessary. If we take care of initializing address Z to 0 (as part of the program load phase), we can substitute CLR by "LOAD Z". If we don't want to initialize the memory in this way we can increment the accumulator until it becomes zero (testing this condition at each iteration):

CLR A|loop: BRZ A, end
       |INC A
       |GOTO loop
       |end: NOP

We can store this initial zero at address 0 and use it thereafter.

4 Problems of the Computing Model

There is one main difficulty with the instruction set mentioned above and it has to do with memory addressing. A Turing machine consists of an unbounded storage tape. There is no addressing problem in this case because the read-write head moves to the left or to the right as necessary. However, in our architecture the absolute address is stored in the address field of each instruction, so that no unbounded memory space can be referenced. If the data size grows beyond the addressable space, the number of bits for each memory word has to be increased, that is, the processor is not fixed in size and can vary according to the problem at hand.

The solution to this difficulty is to use relative addressing. The address in the address field refers then to the current instruction address plus a two's complement offset, stored in the address field of the instruction. The limited size of the address field means that only a certain region around the current instruction can be addressed.

If we now want to simulate a Turing machine, we cannot refer to the storage tape using absolute addresses. If the stored data grows beyond the addressable space, we have to implement a branch to a region in memory closer to the last storage cell. The program must run behind the data being stored in the simulated tape.

Figure 1 shows our solution. A piece of code for the simulation of a universal Turing machine (called TM in the figure) alternates with two fields used to store the i-th bit of the storage tape and the current state of the Turing machine. Moving the read-write head to the right means that the next storage bit is the (i + 1)-th. The simulation jumps to the code below and continues executing. In this way the current bit in the storage tape is never too far away from the instructions being executed. Note that the code for the universal TM has a constant size since its state and output tables have a fixed number of entries.

The length n in bits of the accumulator and memory cells must be large enough to accommodate the opcode of the instructions and to contain the largest relative addresses needed for the emulation of the Turing Machine. Since the size of the TM code is fixed, there exists a finite n fulfilling this condition.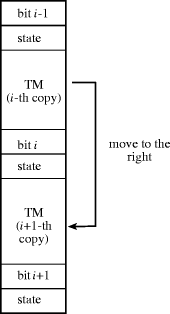

The problem with this scheme is that we do not want to prepare the memory with an infinite number of copies of the simulator of the universal Turing machine. The simulator must copy itself downwards or upwards according to the movement of the simulated read-write head. Remember again that we are not interested in efficiency but only in theoretical realizability.

The simulator of the Turing machine must implement a table look-up. Given the current state and input bit, the new state and the output bit must be determined. This leads naturally to ponder whether conditional branching can be eliminated from the instruction set and substituted by plain unconditional branching. The answer is a resounding yes.

5 The Self-Reproducing Turing Machine

In the following the basic architecture remains unchanged, but now memory addresses refer to cells relative to the address of the current instruction. The instruction set consists of the following instructions with their respective opcodes:

GOTO  00
LOAD  01
STORE 10
INC   11

The opcodes are stored in the highest two bits of the n-bit memory word whereas the lower n - 2 bits are reserved for the address offset.

For the example below we need a portion of the state-transition and output table of the Turing machine. Assume that the two entries for state QN are the following: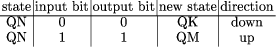

The issue now is how to program the simulator without using any kind of conditional branching. We will use the following trick: assume that the Turing machine has Z states. The coding we will use for state 1 will be "GOTO Q1", where Q1 is the relative address of the memory cell at which the code for processing state Q1 begins, measured relatively to the address with label "state" (see the piece of code below). Similarly state 2 will be represented by the opcode of the instruction "GOTO Q2" etc. We can start the simulation by doing an unconditional branch to the memory cell where the current state is stored (the address labeled "state"). This will then transfer control to the appropriate piece of code. The current tape bit contains a 0 or a 1. According to the opcodes we selected above, this can be interpreted as the instruction "GOTO 0" and "GOTO 1" respectively. Remember that 0 and 1 are the offsets for relative addressing and not absolute addresses. The piece of code below, which includes the trivial macro "MOV", shows how to take advantage of this fact.

    bit: 0
  state: GOTO QN
         .
         .
         .
     QN: INC bit
         MOV bit, instN
  instN: 0
         GOTO zeroN
         GOTO oneN
  zeroN: MOV 0, bit
         MOV "GOTO QK", state below
         GOTO move down
         . 
         . 
         .
   oneN: MOV 1,bit
         MOV "GOTO QM", state above
         GOTO move up

Once the instruction contained in the cell with the label "state" has been executed, control is transferred to label QN. The number in the cell "bit" is incremented and is stored in the cell labeled "instN". If the tape bit was a zero, control is transferred to the instruction immediately below, which in turn jumps to the label "zeroN". If the tape bit was a 1, control is transferred to the second instruction below "instN" and then to the cell labeled "oneN". In both cases we just need to update the i-th tape bit (in our example the updates are different for each case), and the new state. The new state is stored in the state field

above or below the current frame, according to the movement direction of the read-write head. In our example the new state is QK when the read-write head moves down and QM when it moves up. After this is done the simulator must be copied above or below the current frame. This is the most sensitive operation, since it must be done using a loop with a fixed number of iterations, but we do not have any kind of conditional jump in the instruction set. Figure 2 shows how the TM can be copied from one frame to another.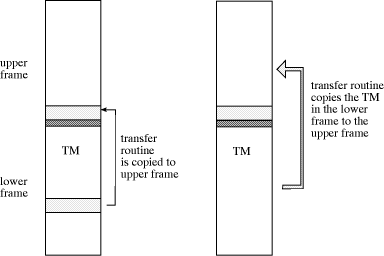

The piece of code which follows copies the simulator of the Turing machine to the upper frame when this is the direction of motion of the read-write head as in our example (shown in Figure 2). The transfer routine is copied first from the simulator to the lower part of the upper frame. Then control is transferred to the address "transfer" and the small routine begins copying the whole TM simulator to the upper frame. Note that the address "frame below" is the first address of the TM simulator and the address "frame" is the first address of the destination for the copy process (the current frame from the point of view of the

copy routine).

    move up: (copy transfer routine
             to upper frame)
             . 
             . 
             .
______________________________________________

    transfer: LOAD frame below    ; start of copy routine
    dest:     STORE frame
              INC transfer
              INC dest
              GOTO transfer       ; end of copy routine
______________________________________________
              .
              . 
              .
              GOTO continue ; last instruction to be copied

The routine copies one word after the other from the frame below to the current frame until the copying process overwrites the first instruction of the copying routine. We only have to take care of aligning the memory so that the instruction "GOTO continue" is copied to the address "transfer". When control is transferred to this address the simulator executes the instruction "GOTO con- tinue+1" and starts again at its new initial position in the upper frame. The first instructions of the simulator can be used to clean-up the results of the copying process and to fix the lower boundary of the simulation program (which requires "GOTO continue" as the last instruction).

We have omitted some details but the reader can fill in the gaps. It should now be clear that we can run the simulation of the Turing machine using only relative addressing and without any kind of conditional jump. The only place at which we need to break a loop is when copying the simulator. This can be done by overwriting the copying routine.

6 Other Possible Minimal Instruction Sets

Some of the early computing machines built in the 1940s did not store the program in the addressable memory. The executable code was punched on a tape which was read sequentially. This was the case of the Z3, built by Konrad Zuse in Berlin, and the Mark I, built by Howard Aiken at Harvard. An interesting question to ask is whether these machines qualify as universal computers. A positive answer would require a proof that we can simulate a Turing machine. Since such a simulation requires an emulator running iteratively, let us assume that both ends of the punched tape can be glued together to obtain an infinite loop. Assume now that the instruction set consists of the instructions:

  LOAD (A)
  STORE (A)
  INC
  DEC

A Turing machine can be simulated by reserving a block of memory for the tape. The position of the read-write head will be indicated by the contents of a memory cell labeled "tape bit". The read-write head can be moved to the left or right by incrementing or decrementing the contents of this memory cell. Simulating the tape is therefore almost as easy as in any conventional computer.

The state of the Turing machine can be updated by looking at tables in memory. Assume that the code for the current state QN is stored in the memory cell "state". The code for this state consists of the address of the memory word in which the next state is stored when the input bit is 0. If the input bit is 1, the next state is stored at an address below. The following piece of code finds the next state according to the contents of the tape bit.

     LOAD (state)    ; load first table entry
     STORE (zero)    ; store into address 0
     INC state
     LOAD (state)    ; load second entry
     STORE (one)     ; store into address 1
     LOAD (tape bit) ; load i-th tape bit
     STORE (bit)     ; store into address 2
     LOAD (2)        ; select table entry according to tape bit
     STORE (state)   ; store as new state

The address with label "zero" contains a 0, that is, a pointer to address 0; the address with label "one" a pointer to address 1, and the address with label "bit" a pointer to address 2. The new state (when the input bit is 0) is stored into address 0. The new state when the input is 1 is stored into address 1. The tape bit is stored into address 2. An indirect load to address 2 recovers the new state and a store to the memory cell "state" updates the state of the Turing machine. Using the same approach the tape bit can be updated performing a table look-up (before updating the machine's state!). Incrementing or decrementing the tape pointer can be done by selecting the appropriate value from a table created at each step:

    LOAD (tape position)
    INC
    STORE (tape inc)
    LOAD (tape position)
    DEC
    STORE (tape dec)
    . 
    . 
    .
    tape bit: 0 ; the contents of these addresses
    tape bit1: 0 ; are modified by the program
    tape bit2: 0 ;

The address "tape position" contains a pointer to the address "tape bit". The addresses "tape inc" and "tape dec" contain pointers to the address one and two positions below "tape bit" (that is, "tape bit1" and "tape bit2"). The correct value can be selected by looking into this small table of two items using the technique discussed above for the case of state updates.

Remember that a Turing machine with a tape extending in only one direction is equivalent to any standard Turing machine. Therefore we do not have any

problems in reserving some addresses (address 0, address 1, etc.) and letting the infinite tape extend upwards in memory. We assume, of course, that the addressable memory is sufficient for the problem at hand and that the bit length of the accumulator is the adequate one. When the computation is finished, the machine can be left looping in a fixed state or an additional "halt" instruction can be added to the instruction set.

We can even eliminate the DEC instruction from the instruction set by remembering that the tape of the Turing machine we are simulating extends in only one direction. We can do the following: if address i represents a bit of the tape, the next bit of the tape will be stored at address i + 2, that is, we leave a free word between them. We then store at address i + 3 the number representing address i, that is a pointer to the previous tape bit. In this way each time the read-write head moves forward we just have to increment the tape position pointer two times. Using an auxiliary memory word we can increment the pointer once again, in order to store the number i at address i + 3. Later on, if the read-write head has to move backwards and if it is currently located at position i + 2, we just have to load the contents of address i + 3 (an address easy to compute using INC) to get address i, that is, the address of the previous tape bit. This is the new value of the tape position pointer. Since decrementing the tape pointer is the only use we have for the DEC instruction, we can omit it safely from the instruction set.

This should suffice to convince the reader that a looping external programs using an instruction set consisting of LOAD (A), STORE (A), and INC (with the assumptions mentioned) are as powerful as conventional computer programs although they still have the problem solved in Section 5, that is, they require a large enough accumulator because they work with absolute addresses. Abstracting from this difficulty, indirect addressing is therefore a building block as powerful as conditional branching. Both the Z3 and the Mark I lacked indirect addressing, although they featured all the arithmetic necessary for our purposes. Had any one of them contained this feature, they would have been, at least in principle, as powerful as modern computers.

7 Summary

We have proved that some minimal instruction sets not including conditional branching are nevertheless sufficient to simulate universal Turing machines. It is mentioned frequently in the literature that conditional branching is needed in universal computers. This is not the case, provided the program can modify itself and unconditional branching plus some other primitive instructions are available in the instruction set. It has also been said that memory-stored programs are a trademark of universal computers. This is also not the case and a simple design with a looping external program capable of indirect addressing suffices to simulate a universal Turing machine.

References

[Corporaal 92] Corporaal, H.: "Evaluating Transport-Triggered-Architectures for Scalar Applications"; Microprocessing and Microprogramming, 38, 1-5, (1993), 45-52.

[Jones 88] Jones, D.W.: "The Ultimate RISC"; Computer Architecture News, 16, 3, (1988), 48-55.

[Minsky 67] Minsky, M.: Computation: Finite and Infinite Machines; Prentice-Hall, Englewood Cliffs, N.J (1967).

[Papadimitriou 94] Papadimitriou, C. H.: Computational Complexity; Addison-Wesley, Reading, MA (1994).

[Patterson, Hennessy 94] Patterson, D., and J. Hennessy: Computer Organization and Design: the Hardware/Software Interface; Morgan Kaufmann, San Mateo, CA, (1994).

[Tabak and Lipovski 80] Tabak, D., and G. J. Lipovski: "MOVE Architecture in Digital Computers"; IEEE TRansactions on Computers, (1980), 180-189.

[Wolfram 86] Wolfram, S.: Theory and Applications of Cellular Automata; World Scientific, Singapur (1986).