| Submission Procedure |
An Efficient Distributed Algorithm For st-numbering the Vertices of a Biconnected Graph
(Indian Institute of Technology, Madras, India) (Indian Institute of Technology, Madras, India rangan@iitm.ernet.in) Abstract: Given a biconnected network G with n nodes and a specific edge (r, s) of G, the st-numbering problem asks for an assignment of integers to the nodes satisfying the following condition: r is assigned the number 1 and s is assigned the number n and all other nodes are assigned numbers in such a way that every node (other than r and s) has a neighbour with smaller st-number and a neighbour with larger st-number. Since st-numbering exists iff G is biconnected, it serves as a powerful "local characterization" of the "global" property of the network. We present an efficient O(e) message complexity and O(n) time complexity algorithm for st-numbering a biconnected graph. Key Words: Distributed graph algorithms, st-numbering, biconnected graph Category: G.2.2 1 Introduction
In almost every application implemented in a distributed system, we often find it necessary to use certain network functions such as traversal through the network, learning of global information not initially known by the sites and determination of optimal routes between the sites. Such network functions, if available at each site, will spare the application programs the pain of handling directly information transfers and the associated controlling tasks. The algorithms for such network functions are known as network algorithms or distributed graph algorithms. Distributed graph algorithms are known for a wide variety of graph problems. See [Raynal 1987] [Leeuwen 1990] for a comprehensive discussion on this topic. In this paper we are concerned with the computation of st-numbering (to be defined later) for a biconnected network. Informally, st-numbering is a numbering scheme in which we number the vertices in such a way that every vertex has at least one neighbour with a larger number and one neighbour with a smaller Page 633 number associated with it. Such a numbering scheme not only gives a structural characterization of the network but also enables one to identify internally vertex disjoint routes between a pair of sites. In another paper, we have discussed the application of st-numbers to construct the centered spanning tree studied in [Cheston et al. 1989] [Easwarakumar et al. 1994]. 2 Model
Consider a distributed computing system consisting of a number of autonomous processors interconnected through a network of communication links. The processors do not share common memory, have no global clock and communicate with each other only by passing messages. The interconnection network can be modeled by an undirected communication graph G = (V, E) where nodes correspond to the processors and the edges correspond to the bidirectional communication links. When we look at G as a graph, we refer to elements of V as vertices and when we look at G as a network, we refer to them as nodes. The exchange of messages between two neighbouring processors is asynchronous. The communication subsystem, we assume will deliver the message at its destination without loss after a finite but unbounded delay. The messages sent over any link follow a FIFO rule. The messages received at any processor are transferred to a common queue before being processed. Messages arriving at a node simultaneously from several neighbours may be placed in any arbitrary order in the queue. The following complexity measures are used to evaluate performances of distributed algorithms operating in the above network. The communication or message complexity is the total number of messages sent during execution of the algorithm. The time complexity is the maximum time passed from its start to its termination, assuming that the time of delivering a message over each link is at most one unit of time and the computation complexity at each node is negligible. No time out of any sort is assumed and the bounded delay is assumed only for evaluating the time complexity. The algorithm operates correctly with any finite arbitrary message-delivery time. 3 Definitions and Properties
Let G(V, E) be a biconnected graph. The degree of a vertex v is the number of vertices adjacent to v in G. An undirected edge from u to v is denoted by (u, v). Page 634 Let n denote the number of vertices in the graph. Definition 2.1 For
an edge (r, s) of a biconnected graph G, a one-to-one function g: 1. g(r) = 1 2. g(s) = n 3. for every It is well known that a graph is biconnected iff it admits an st-numbering with respect to every edge [Even and Tarjan 1976] [Ebert and Koblenz 1983]. Definition 2.2 Let T be a DFS (Depth First Search) tree rooted at r. Define
Definition 2.3 The height HEIGHT(T) of a rooted tree is
The Depth First Search (DFS) tree of a graph G, splits the
edge set of G into two disjoint sets, the set of tree edges and the
set of back edges. Denote a tree edge (v, w) by Remark: We usually imagine that the edges of the DFS tree are oriented "away" or "downwards" from the root. Also, a non-tree edge can exist only between a pair of vertices with one of them an ancestor of the other. That is why, the non-tree edges are called back edges and we always assume that back edges are oriented "upwards" or "towards" the root. Definition 2.4 Define
DFS(v), where Definition 2.5 [Tarjan 1972]
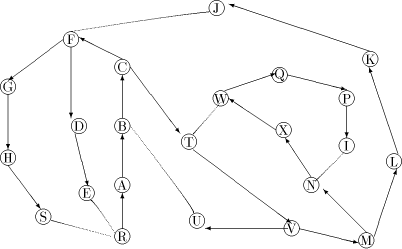
For all Definition 2.6 [Ebert and Koblenz 1983] For all For a given node, there may be more than one node which satisfies this Page 635 definition. In such cases any arbitrary assignment is made. For example, in [Fig. 2], both G and D are candidates for the low-child(F). Definition 2.7 For all Definition 2.8 For all We now state some properties of DFS trees. Henceforth, we denote the DFS tree by T and assume that T is rooted at the vertex r. Lemma 1 [Tarjan 1972]: G is biconnected, iff 1. there is exactly one tree
edge 2. low(u) = DFS(r), and 3. low(w) < DFS(v) for all other tree edges Lemma 2 [Tarjan 1974]: There
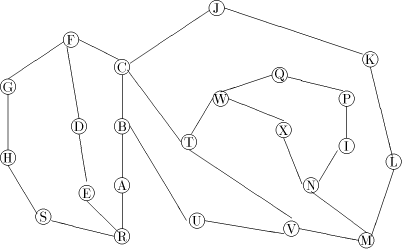
is a path Note, that in order to find an st-numbering with respect to (r, s), s should not be the child of r in T. Therefore by lemma 1, (s, r) will be a back edge. This is clear from the DFS tree in [Fig. 2], for the sample graph in [Fig. 1].
Figure 1: A sample graph G Page 636
Figure 2: The DFS tree T Definition 2.9 For all Definition 2.10 The graph defined by (V, {(v, next1(v)): - - Let Page 637
Figure 3: The graph Lemma 3 [Ebert and Koblenz 1983]: If 1. DFS(x) < DFS(v) for all 2. low(x) = low(v) for all v on 3. DFS(parent(x)) Proof: The proof follows from the definition [Section 2.9] of next1. Definition 2.11 Let P denote
the path Definition 2.12 Again, consider the auxiliary graph
Clearly Page 638 path in See [Fig. 2] [Fig. 3] [Fig. 4] for a clear description of the above definitions.
Figure 4: The graph Lemma 4 [Ebert and Koblenz 1983]: If 1. DFS(x) < DFS(v) for all 2. low(x) = low(v) for all v on 3. DFS(parent(x)) Definition 2.13 For any node We have already noted
that Lemma 5: An
edge Proof: The result follows by the definition of next1 and next2. Definition 2.14 For every tail
vertex v of Page 639 For example, in [Fig. 4], J is a tail vertex and low(J) is C. Therefore C is the par_sign_vertex of J. T is that child of C which is an ancestor of J. Therefore sign_vertex of J is T. Lemma 6: Every tail vertex except s has a sign_vertex. Proof: Let Definition 2.15 Define head_sum(u) for any By lemma 5, 4 Algorithm
4.1 Stage 1
The first stage of our algorithm is fully devoted to finding the Depth first Search numbers and other tree functions we introduced in the previous section. Specifically, we compute DFS(v), low(v), low-child(v), next1(v), parent(v), dfs_ch(v) and desc(v) for every node v. The DFS starts at the node r and chooses a node other than s as the son of r. Thus r is the root of the DFS tree and the edge (r, s) will be a back edge. Our computation closely follows the DDFS algorithm presented in [Lakshmanan et al. 1987] [Cidon 1988]. The DDFS algorithms in [Lakshmanan et al. 1987] [Cidon 1988] use the message TOKEN or DISCOVER to effect a forward phase and a backward phase. Informally, the forward phase carries the message from root to leaves and the backward phase does just the opposite. In the forward phase, DFS(v) and parent(v) are computed by piggybacking the DFS number of the sending node onto the TOKEN or DISCOVER message while in the backward phase desc(v) and low(v) where v is the node sending the message are piggybacked and low(v), low_child(v), next1(v), dfs_ch(v) and desc(v) are computed. Also, the DFS number is piggybacked onto the VISITED message. Page 640 Stage 1 terminates at the root node r upon receiving the message DISCOVER or TOKEN in the backward phase. Basically, both next1 and next2 decompose the DFS tree into maximal paths. The major (and only) difference is that next2 has the trunk path as one of its maximal paths while the definition of next1 is independent of s. Thus, next1 may be constructed explicitly while the DFS tree is built but next2 is (dynamically and implicitly) constructed while the st-numbering is done. 4.2 Stage 2
In this phase, we label each maximal path as either ASC or DESC and the trunk path as TRUNK. The intuitive idea behind such a task is to allocate the st-numbers for the vertices in a maximal path in the increasing or decreasing order (from head to tail) depending on its label (ASC, DESC or TRUNK). The st-numbers for vertices in the TRUNK path will always be in the increasing order. In order to label the maximal paths in a meaningful way, we put the nodes into one of the following 4 states TRUNK DESC ASC NORMAL All the nodes will initially be in the NORMAL state. They will then move into one of the three states (TRUNK, ASC, DESC). The following messages are used in this stage: TRUNK(l, m) PROBE(c) BEGIN SIGN(c) ECHO(c) STN(p, q) We also use the following state transition function called change which is defined as follows change(TRUNK) = DESC change(DESC) = ASC change(ASC) = DESC Page 641 Stage 1 terminates at r and after the termination of stage 1, the root r will initiate stage 2, by sending a message TRUNK(n, 0) to s via the back edge (s, r). Then the node s sends BEGIN message to all its children in the DFS tree and sends TRUNK(n - desc(s), desc(s)) to parent(s). Thus the second stage begins with identifying the trunk path. The node s, which is the tail of the trunk path initiates the task of identifying the trunk. We identify the nodes in the trunk path by passing the TRUNK messages. In the message TRUNK(l, m) sent by a node in the trunk path, l denotes the st-number assigned to the node receiving the message and m denotes the number of descendants of the node sending the message. When a node Observe that, TRUNK messages, pass through only the trunk path while BEGIN messages travel along other maximal paths. Also, once a node receives the TRUNK or BEGIN message it knows whether it is on the trunk path or not and can compute next2 and ch_st. Thereafter it can compute head_sum. Our goal now, is to
determine if a non-trunk maximal path is an ASC or DESC path. Let Hence the tail_vertex does the following Step 1 Send messages to get the information on the state of sign_vertex(y). Step 2 Propagate using the state transition function "change", the new state of all nodes on the maximal path along the maximal path to x and then to Page 642 parent(x). Step 1 is carried out as follows When a tail node t receives the message BEGIN, it sends PROBE(1) to par_sign_vertex(t) along the edge (t, par_sign_vertex(t)). Note that, by lemma 3, par_sign_vertex(t) can determine the sign_vertex(t). After receiving PROBE(1), par_sign_vertex(t) sends the message PROBE(2) to sign_vertex(t). Recall that the sign_vertex(t) was initiated to NORMAL state. If it is in the NORMAL state it does not respond to PROBE(2). If sign_vertex(t) has changed to some other state (one of TRUNK, ASC, DESC), it is ready to respond. Now sign_vertex(t) sends the message ECHO(c) to par_sign_vertex(t), which in turn sends the message to t. Here c denotes the current state of sign_vertex(t). In summary, t sends PROBE message via par_sign_vertex(t) to x and x sends ECHO(c) message to t via par_sign_vertex(t). Step 2 is carried out as follows When t receives the ECHO(c) message it sends SIGN(change(c)) to parent(t). It also changes its state from NORMAL to change(c). The SIGN(change(c)) travels all the way up in the maximal path for which t is a tail and reaches the head say h of the maximal path. From h, the message SIGN(change(c)) goes one step further along the edge (h,parent(h)), and reaches the node parent(h). As the SIGN(change(c)) message travels up from t to h, we keep updating the state to change(c) for every node including h. This completes the description of stage 2. Thus, at the end of stage 2, the parent(h) where h is the head node of a maximal path, knows the state of h. Lemma 7 A finite time after r sends the TRUNK(n, 0)
message nodes on the path Proof: Obvious. Lemma 8 A finite time after r sends the TRUNK(n,0) message every tail node will change its state, and by that every node on the maximal path ofthat tail node will change state. Proof: By
lemma 7, every tail node will receive the BEGIN message and all trunk
nodes would have received TRUNK message. Therefore, the state of the
trunk nodes would have changed to TRUNK. By lemma 6, every tail node
has a sign_vertex. Thus, all the maximal paths Page 643 Lemma 9 The state of all nodes on a maximal path changes according to the state transition function "change" depending on the state of the sign_vertex of the tail vertex. Proof: Obvious. Lemma 10 A finite time after r sends the TRUNK(n, 0) message, every node which has child vertices which are head nodes will have received a SIGN message from each of these nodes. Proof: By lemma 7 and lemma 8, the result is easily proved. 4.3 Stage 3
For this stage of the algorithm each node computes two values i.e. ST_LOW and ST_HIGH. The st-number assignment of nodes on the trunk is done when the TRUNK message arrives while at all other nodes it will be done by STN messages. The new state that the nodes of a maximal path reach, indicates the direction of assignment of the st-numbering along the maximal path. If the state of the nodes are DESC then the st-number will be in descending order from head vertex to tail vertex and in the other way for the nodes in ASC state. This stage proceeds concurrently with stage 2. 4.3.1 Algorithm at trunk nodes
When a trunk node u receives the TRUNK(l, m) message it assigns itself the st-number l. It then initialises st_high to l-1 and st_low to l+m-desc(u)+1. It also sends TRUNK(l+m-desc(u), desc(u)) to parent(u). Whenever u receives a SIGN message from a child v (which ought to be a head node of a maximal path), u assigns v a chunk of st-numbers in the range [st_high - desc(v) + 1...st_high] by sending the STN(st_high - desc(v) + 1, st_high) message to v. It updates st_high to st_high - desc(v). It repeats this procedure until it has received a SIGN message from every child except the one on the trunk. At this point the algorithm at this node terminates. For example, node F receives TRUNK(20, 3) from G and sends TRUNK(17, 6) to C. F receives the SIGN(DESC) message from D and sends D STN(18, 19). Lemma 11 The algorithm at a trunk node u terminates. Proof: The trunk node u receives a SIGN message after it receives the TRUNK message, since for any non-trunk child v, of u, low(v) < DFS(u). Also low(v) Page 644 points to an ancestor of u(lemma 1) and therefore the sign_vertex does not change state before u receives the TRUNK message. Thus, once u changes its state it will receive SIGN messages from all its children which are head nodes. As these messages are received u responds with an STN message. By lemma 10 u receives SIGN messages from all its children which are head nodes. Lemma 12 When a trunk node assigns, an interval of st-numbers to its nontrunk (head node) child v in the DFS tree, the numbers are sufficient and granted exclusively for all the nodes which are descendants of v. Proof: Observe that v receives an interval consisting of desc(v) numbers. Lemma 13 The st-numbers assigned to the nodes on the trunk path will be in increasing order with g(r) = 1 and g(s) = n. Proof: Clearly, by the movement of the message TRUNK(n, 0) along the edge (r, s) the st-number assigned to s will be n. Now, the st-number assigned to the parent of a node u where u is on the trunk is n - desc(u). This can easily be proved by induction on the nodes of the trunk. Thus, the st-number assignment will be in decreasing order from s to r. By, lemma 1, r has exactly one child v in the DFS tree which is on the trunk. Therefore desc(v) = n - 1. Thus g(r) = 1. Hence the lemma. 4.3.2 Algorithm at other nodes
In general every non-trunk node will receive an interval or a continuous chunk of numbers to be assigned to itself and to its descendants, so that the numbers assigned satisfy the st-numbering properties. Thus, every node u will receive an interval of the form [a, a + desc(u) - 1] via the message STN(a, a + desc(u) - 1) from its parent in the DFS tree. Now, let ch_set(v) = When u receives the message STN(p, q), it initialises two variables st_high to q and st_low to p. If u is in the state ASC it sends the interval [st_low + head_sum(u) + 1...st_high] to next2(u) if next2(u) exists by sending the message STN(st_low + head_sum(u) + 1, st_high) along the edge (u,next2(u)). After sending the interval, it updates st_high to st_low + head_sum(u). If however, u is in the state DESC it sends the interval [st_low...st_high - head_sum(u) - 1] to next2(u) if next2(u) exists by sending the message STN(st_low, st_high - head_sum(u) - 1) along the edge (u, next2(u)) and updates st_low to st_high - Page 645 head_sum(u). Note that if u is a tail node then next2(u) will be nil and hence no interval will be sent and no update will take place in this case. Having sent the STN message to next2(u), u is ready to
send intervals to the members of ch_set(u) once it receives SIGN
messages from these nodes. After u receives the SIGN(ASC) message
from After sending st-number intervals in the above fashion to all the members of ch_set(u), u will be left with an interval of unit size, that is st_low = st_high. Now, u takes st_low as its st-number and terminates. For example, in [Fig. 5], the maximal paths with M and N as head nodes will be in ASC state while the maximal paths with Q and T will be in DESC state. We shall consider the algorithm at V. It receives STN(4, 15) from T. It also receives SIGN(ASC) from its only child which is a head node, M. It sends U the node which is on the same maximal path as V STN(4,4). It sends M STN(6, 15) and will be finally left with the interval [5, 5] and assigns itself the st-number 5. The final st-numbering for the sample graph is in [Fig. 5]. Lemma 14 When a non-trunk node assigns an interval of st-numbers to its (head node) child v in the DFS tree, the numbers are sufficient and granted exclusively for all the nodes which are descendants of v Proof: Obvious. Lemma 15 The st-number of nodes in a maximal path
Proof: If the state of the node u is DESC, then the interval of st-numbers allotted to its child node v in the maximal path is (st_high - head_sum - 1, st_low) where u and v lie on the maximal path. The interval retained for the node u itself is (st_high, st_high - head_sum) which is clearly larger than that allotted to v. Since, the st-number allotted for u is from this interval, the result follows. Page 646
Figure 5: The graph Lemma 16 The st-number of nodes in a maximal path Proof: Similar to lemma 15. Lemma 17 The algorithm at non-trunk nodes terminates Proof: By lemma 10, the node would have received all the required SIGN messages. Thus a non-trunk node which has received a STN message would have sent a STN message to all its children in the DFS tree. Thus, it is easily proved that the STN message reaches all the non-trunk nodes. Lemma 18 The st-number interval assigned by a non-trunk node x to a child u which is a head node, is greater than the st-number assigned to itselfifthe state of u is ASC. Proof: x sends the interval [st_high...st_high-desc(u)+ 1] and reduces its range to [st_high - desc(u), st_low] from which its own st-number is assigned. Also, by lemma 12 the range of st-numbers available to x is sufficient. Thus the result follows. Lemma 19 The st-number interval assigned by a non-trunk node x to a child u which is a head node, is lesser than the st-number assigned to itself if the state of u is DESC. Proof: By an argument similar to lemma 18 the result follows. Page 647 Theorem 1 The algorithm correctly assigns st-numbers to the entire network. Proof: By lemma 13, g(r) = 1 and g(s) = n and property 3
(def. 2.1) is satisfied by all internal nodes of the trunk path. By
lemma 12, 14, 15 and 16 property 3 is satisfied by all the internal
nodes of non-trunk maximal paths and the st-number range assigned is
sufficient. It remains to show that every head and tail node has a
smaller and a larger neighbour. Consider a maximal path case 1: z is a trunk node. By lemma 1 and 4 p should be an ancestor of z. Thus the state of all nodes on the maximal path should be DESC(lemma 9). Clearly, the st-number range allotted to x by z is less than the st-number assigned to z. Therefore st-number assigned to x is less than that assigned to z. Also, the st-number range allotted to any of z's ancestors on the trunk path is smaller than the st-number range allotted to x. To be specific, st-number assigned to p is smaller than the st-number assigned to y. Thus property 3 [see Section 2.1] is also satisfied for x and y. For example, in [Fig. 4], for the maximal path with T as head node, parent(T) C lies on the trunk path and B is the par_sign_vertex while C is the sign_vertex of U. case 2: z is not a trunk node. By lemma 18 and 19 property 3 [Section 2.1] is satisfied for x. It remains to show that it is satisfied for y, the tail node. Assume y is in the state ASC. We shall prove that st-number of p is larger than y. Let u be the sign_vertex of y. By lemma 9, the state of u is DESC. Now, consider two cases case a: p is on the same maximal path as u. Clearly, the st-number range sent by p to u is smaller than the range retained for itself. Since, (lemma 1 and 4) x and y are descendants of u, the result follows. For example, in [Fig. 4], for the maximal path with Q as head node, W is the parent(Q) and N is the par_sign_vertex while X is the sign_vertex of I. Both N and X lie on the same maximal path. case b: p is not on the same maximal path as u This implies that u is the head vertex of a maximal path with state DESC. p is the parent of u and by lemma 19 the range of st-numbers assigned to u is less than the st-number assigned to p. Thus by lemma 1 and 4 the result follows. Page 648 For example, in [Fig. 4], for the maximal path with M as head node, V is the parent(M) and C is the par_sign_vertex while T is the sign_vertex of J. If y is in state DESC, u maybe in ASC or TRUNK. The proof for the case u is ASC is similar to the proof given above. If u is in state TRUNK, then p also must be on the trunk and clearly st-number of p is less than that of all vertices in the maximal path, which all have u as an ancestor. Therefore, by lemmas 11 and 17, the algorithm terminates correctly. 5 Complexity
The message and time complexity of stage 1 is 3*e and 2*n-2 respectively [Cidon 1988]. Let the number of trunk nodes i.e. nodes
in the path The probe/echo interaction will require 4 messages per tail vertex and the total probe/echo message complexity is therefore 4 * q. Each non-trunk node sends a SIGN message and this complexity is n - p. By an argument similar to the above, the time complexity will in this case also be bounded by the message complexity. Each non-trunk node receives one STN message and therefore the total number of STN messages are n - p. The time complexity here also is bounded by n - p. The above complexity details are summarised in the following table.
Table 1: Complexity Page 649 Clearly the message bit complexity at any stage of the algorithm is O(log n). Hence, we state the following theorem. Theorem 2 The message complexity of the algorithm is O(e), the time complexity O(n) and the message bit complexity O(log(n)). 6 Conclusions
This paper presents the first distributed algorithm for st-numbering a biconnected graph. st-numbers are among the non-trivial node functions and is extensively used in a variety of graph problems including the planarity test [Even 1979]. Since a graph is biconnected iff it admits an st-numbering of its vertices, we see that this function is a powerful characterization of the entire structure of the network in terms of extremely simple local information. Such characterizations are very critical in the context of distributed computing where the fundamental assumption is that every node knows only its neighbours and not the entire network. Since every node has a smaller and a larger neighbour, it is easy to see how one can construct internally vertex disjoint paths between a pair of given vertices. Elsewhere, we show an interesting application of the st-numbers for the centering of a spanning tree in a biconnected network [Easwarakumar et al. 1994] [Aranha and Rangan 1994]. References
[Cheston et al. 1989] Cheston, G.A., Farley, A., Hedetniemi, S.T., Proskurowski, A.: "Centering a spanning tree of a biconnected graph": Information Processing Letters 32, (1989), 247-250. [Even and Tarjan 1976] Even, S., Tarjan, R.E.: "Computing an st-numbering": Theoretical Computer Science (1976), 339-344. [Even 1979] Even, S.: "Graph Algorithms": Computer Science press, USA (1979). [Lakshmanan et al. 1987] Lakshmanan, K.B., Meenakshi, N., Thulasiraman, K.: "A time optimal message-efficient distributed algorithm for dept-first-search": Information Processing Letters 25, (1987), 103-109. [Cidon 1988] Cidon, I.: "Yet another distributed depth-first-search algorithm": Information Processing Letters 26, (1988), 301-305. [Ebert and Koblenz 1983] Ebert, J., Koblenz,: "st-ordering the vertices of biconnected graphs": Computing 30, (1983), 19-33.
Page 650 [Tarjan 1972] Tarjan, R.E.: "Depth-first search and linear graph algorithms": SIAM J. of Computing 1, (1972), 146 - 160. [Tarjan 1974] Tarjan, R.E.: "Finding dominators in directed graphs": SIAM J. of Computing 3, (1974), 62 - 89. [Raynal 1987] Raynal, M.: "Networks and distributed computation": North Oxford Academic Press (1987). [Leeuwen 1990] Leeuwen, J.V.: "Formal models and semantics": Handbook of theoretical computer science, vol. B. Elsevier Publishers (1990). [Easwarakumar et al. 1994] Easwarakumar, E.S., Rangan, C.P., Cheston, G.A.: "A linear algorithm for centering a spanning tree of a biconnected graph": Information Processing Letters 51, (1994), 121-124. [Aranha and Rangan 1994] Aranha, R.F.M., Rangan, C.P.: "An efficient distributed algorithm for centering a spanning tree of a biconnected graph": (submitted) (1994).
Page 651
|
|||||||||||||||||
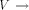 {1,2,...,n} is called an st-numbering with respect to (r, s) if
the following conditions are satisfied.
{1,2,...,n} is called an st-numbering with respect to (r, s) if
the following conditions are satisfied.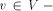 {r, s} there are adjacent vertices u and w such
that g(u) < g(v) < g(w).
{r, s} there are adjacent vertices u and w such
that g(u) < g(v) < g(w).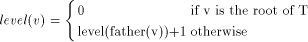
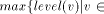
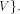
 and a back
edge by
and a back
edge by 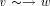 . A path from v to w consisting of zero or more edges
is denoted by
. A path from v to w consisting of zero or more edges
is denoted by 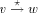 .
. 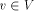 , to be k if v is the k-th vertex to be
processed in the formation of the DFS tree. Clearly DFS(v) is the
preorder number of v in the DFS tree, T.
, to be k if v is the k-th vertex to be
processed in the formation of the DFS tree. Clearly DFS(v) is the
preorder number of v in the DFS tree, T.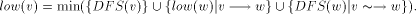

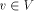 define desc(v) to be the number of descendants of v in the DFS tree, including v.
define desc(v) to be the number of descendants of v in the DFS tree, including v. in the DFS tree T.
in the DFS tree T. .
.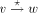 in the DFS tree T iff
in the DFS tree T iff 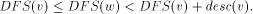
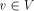 define
define 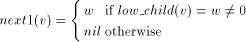
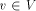 }) is
denoted by
}) is
denoted by 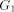 and it is clear that
and it is clear that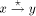 be a component path. Then x is referred to as the head
vertex and y as the tail vertex. Note that, a vertex x is a head
vertex iff the parent z of x in the DFS tree satisfies the condition
that next1(z)
be a component path. Then x is referred to as the head
vertex and y as the tail vertex. Note that, a vertex x is a head
vertex iff the parent z of x in the DFS tree satisfies the condition
that next1(z) 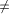 x. That is, x is not the low_child(z). Clearly, a
node y is a tail vertex if next1(y) = nil.
x. That is, x is not the low_child(z). Clearly, a
node y is a tail vertex if next1(y) = nil.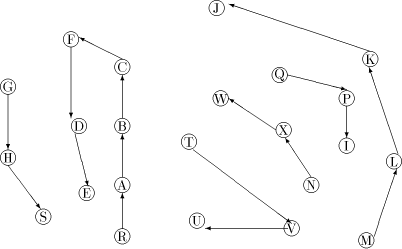
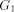
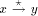 , is a component path in
, is a component path in 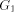 the following assertions hold:
the following assertions hold: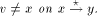
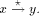
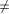 low(x).
low(x).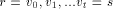 from r to s in the DFS tree T. By an
abuse of notation let P also denote the set of vertices in the path P. Now define for all
from r to s in the DFS tree T. By an
abuse of notation let P also denote the set of vertices in the path P. Now define for all 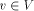
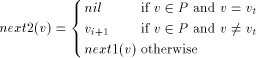
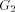 formed as follows.
formed as follows.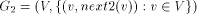
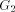 is also a
subgraph of the DFS tree T and
is also a
subgraph of the DFS tree T and 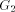 consists of one or more paths which
we refer to as maximal paths. As in the case of
consists of one or more paths which
we refer to as maximal paths. As in the case of 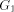 we can define head
and tail vertex for the graph
we can define head
and tail vertex for the graph 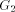 and we refer the same as the trunk path.
and we refer the same as the trunk path.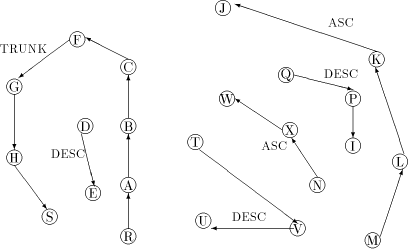
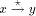 , is a non-trunk
maximal path in
, is a non-trunk
maximal path in that is,
that is, then the following
assertions hold:
then the following
assertions hold: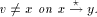
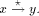
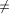 low(x).
low(x).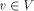 , let dfs_ch(v) denote
the set of all children of v in T, that is dfs_ch(v) =
, let dfs_ch(v) denote
the set of all children of v in T, that is dfs_ch(v) =  . Define, ch_set(v) = dfs_ch(v) - next2(v).
. Define, ch_set(v) = dfs_ch(v) - next2(v).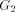 is a subgraph of the DFS tree T.The following lemma
characterizes the edges of T that are not in
is a subgraph of the DFS tree T.The following lemma
characterizes the edges of T that are not in 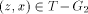 iff x is a head vertex of a maximal path and z is
its parent in the DFS tree T.
iff x is a head vertex of a maximal path and z is
its parent in the DFS tree T.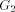 except s, there exists a back edge of the form
except s, there exists a back edge of the form 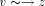 where low(v) = DFS(z). Let t be that child of z, which is an
ancestor of v in the DFS tree T. Then t, is called the sign_vertex of
v and z is the par_sign_vertex of v.
where low(v) = DFS(z). Let t be that child of z, which is an
ancestor of v in the DFS tree T. Then t, is called the sign_vertex of
v and z is the par_sign_vertex of v.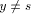 be a tail vertex such that low(y) = DFS(z). Then, there exists a back
edge
be a tail vertex such that low(y) = DFS(z). Then, there exists a back
edge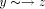 . Clearly, z is an ancestor of y. Therefore there exists
a path
. Clearly, z is an ancestor of y. Therefore there exists
a path 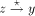 . Let x be the head node of the maximal path on which y
lies. By lemma 4, low(x) = DFS(Z). Thus by lemma 1, there exists a
vertex
. Let x be the head node of the maximal path on which y
lies. By lemma 4, low(x) = DFS(Z). Thus by lemma 1, there exists a
vertex 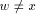 such that,
such that, 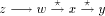 is a path in T since
is a path in T since 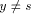 Thus w is the sign_vertex and the lemma follows.
Thus w is the sign_vertex and the lemma follows.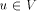 to be the sum of
desc(x) where x is a child of u and x is a head vertex.
to be the sum of
desc(x) where x is a child of u and x is a head vertex.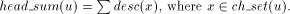
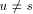 receives the
TRUNK(l, m) message it will assign itself the st-number l and move
into the TRUNK state. It will then send TRUNK(l+ m-desc(u), desc(u))
to parent(u). Thereafter it sends a BEGIN message to every child
except next2(u). Thus we note that the TRUNK messages, propagated
from s moves up and marks all the nodes of the trunk path and changes
their states to TRUNK and ends at the root. On its way up, it assigns
the st-number for each node and initiates the computation of head_sum
and propagates BEGIN messages to all other non-trunk nodes. When a
node receives the BEGIN message from its parent it will pass on the
BEGIN message to all its children in the DFS tree. The receipt of the
TRUNK or BEGIN message initiates the algorithm at each node. When the
root r receives the TRUNK message it simply changes its state to
TRUNK and does nothing.
receives the
TRUNK(l, m) message it will assign itself the st-number l and move
into the TRUNK state. It will then send TRUNK(l+ m-desc(u), desc(u))
to parent(u). Thereafter it sends a BEGIN message to every child
except next2(u). Thus we note that the TRUNK messages, propagated
from s moves up and marks all the nodes of the trunk path and changes
their states to TRUNK and ends at the root. On its way up, it assigns
the st-number for each node and initiates the computation of head_sum
and propagates BEGIN messages to all other non-trunk nodes. When a
node receives the BEGIN message from its parent it will pass on the
BEGIN message to all its children in the DFS tree. The receipt of the
TRUNK or BEGIN message initiates the algorithm at each node. When the
root r receives the TRUNK message it simply changes its state to
TRUNK and does nothing.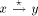 be a maximal path. We stipulate that this path is an ASC path if
the state of sign_vertex(y) is DESC and it is a DESC path if the
state of sign_vertex is ASC or TRUNK. The justification for such a
labeling will be given later.
be a maximal path. We stipulate that this path is an ASC path if
the state of sign_vertex(y) is DESC and it is a DESC path if the
state of sign_vertex is ASC or TRUNK. The justification for such a
labeling will be given later.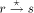 will receive the TRUNK message and
all the other nodes will receive the BEGIN message.
will receive the TRUNK message and
all the other nodes will receive the BEGIN message.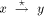 where
sign_vertex(y)
where
sign_vertex(y)  TRUNK will change their state. Extending, all
other maximal paths will also change their state.
TRUNK will change their state. Extending, all
other maximal paths will also change their state. where state of
where state of 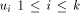 is ASC and state of
is ASC and state of 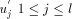 is DESC.
is DESC.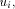 , it sends the interval [st_high - desc(ui) + 1...st_high] to
, it sends the interval [st_high - desc(ui) + 1...st_high] to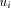 by sending the message STN(st_high - desc(ui) + 1, st_high) along
the and updates st_high to
by sending the message STN(st_high - desc(ui) + 1, st_high) along
the and updates st_high to 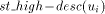 . After u
receives the SIGN(DESC) message from
. After u
receives the SIGN(DESC) message from 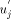 it sends the interval
it sends the interval 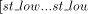
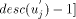 by sending STN
by sending STN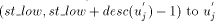 along
along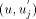 and updates st_low to st_low +
and updates st_low to st_low + 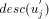 .
.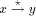 will be in descending order from x to y, if the state of the
nodes in the maximal path is DESC.
will be in descending order from x to y, if the state of the
nodes in the maximal path is DESC. 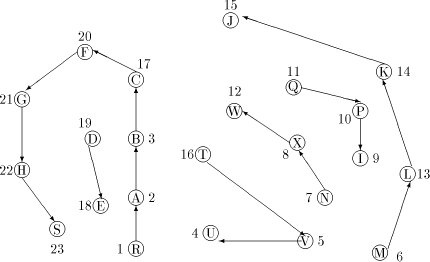
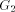 with st-numbers assigned
with st-numbers assigned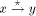 will be in
ascending order from x to y, if the state of the nodes in the maximal
path is ASC.
will be in
ascending order from x to y, if the state of the nodes in the maximal
path is ASC. 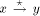 . Let z
denote the parent of x i.e. z = parent(x). Let p be the node such
that DFS(p) = low(x) = low(y) that is, p is the par_sign_vertex(y).
. Let z
denote the parent of x i.e. z = parent(x). Let p be the node such
that DFS(p) = low(x) = low(y) that is, p is the par_sign_vertex(y).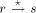 be p. Let the number of maximal paths
be p. Let the number of maximal paths 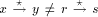 be q. Each trunk node will send a TRUNK message and the total
number of TRUNK messages will thus be p. On every other edge of the
DFS tree a BEGIN message is transmitted and therefore the message
complexity of this part of the algorithm is n. At every unit of
time, at least one more message is sent and therefore the time
complexity is at most n.
be q. Each trunk node will send a TRUNK message and the total
number of TRUNK messages will thus be p. On every other edge of the
DFS tree a BEGIN message is transmitted and therefore the message
complexity of this part of the algorithm is n. At every unit of
time, at least one more message is sent and therefore the time
complexity is at most n.