| Submission Procedure |
Special Cases of Division
(The University of Auckland, New Zealand bob@cs.auckland.ac.nz) Abstract: This surveys algorithms and circuits for integer division in special cases. These include division by constants, small divisors, exact divisors, and cases where the divisor and the number base have a special relationship. The related operation of remainder is also covered. Various prior techniques are treated in a common framework. Worked examples are provided together with examples of practical application. Category: B2.0 Arithmetic and Logic Circuits 1 Introduction
Division, although known in theory to be capable of O(log n) solution [Beame, Cooke and Hoover 1986], is difficult to implement with high performance in practice. However, there are many special cases where division is much easier, so that fast algorithms may be used. Many 'tricks' have been discovered over the years. Some of these are not well known and there are others that are familiar to practitioners but have not been described in the literature that is easy to access. The purpose of this paper is to survey the special cases of division and describe them in a uniform manner. We will consider only non-negative integers, extended to fixed-point number representation in some cases. 1.1 Notation
To describe division we will use the notation: In general, division is the process that, given D and d, finds q and r
so that D = q*d + r where We will assume that integers are presented, using a positive integer base b, as n-digit vectors. In particular we have D, d, q, r, where, for example:
The values We will often use base 10 in examples although most circuits will use binary representation in practice. 1.2 Relationship between div and mod
Page 176 The operations of division and remaindering are closely related and are reducible to each other. That the remainder can be found after division is obvious, for: r = D mod d = D - (D div d)*d = D - q*d Knowledge of the remainder can reduce division to the special case where the dividend is an exact multiple of the divisor, for D - (D mod d) = q*d. This can simplify the process of division in some circumstances to be covered below. However, the ability to perform remaindering can allow the quotient to be derived without further division, but the process depends on the representation of the numbers and the standard algorithm for division. Write The standard process of division is to produce the quotient digits
At each step we have to perform the division expressed by Thus the standard process allows us to use remaindering to reduce
general division to steps that involve division that produces a small
quotient (the We now have division that is exact and with a small quotient. Because
Page 177
In even more-special cases the process of finding the quotient digits is further simplified. For example, because
In summary, if the values
Figure 1: Derivation of quotient from remainders 2 Small quotient
There are sometimes circumstances where it is known that the quotient
is small, so that we can find it by using case analysis. Because D =
d*q + r, for each possible q' we know that q = q' iff One situation arose in the standard division process above where we
needed to find each Example:
Page 178 Another situation arises in arithmetic modulo d where x < d and we want to form (x * y) mod d, where y < b, the number base, which is small. Setting D = x*y, and q = D div d, we know that q < b. Because there are only a limited number of possibilities for the quotient, it can be found first and used to calculate the remainder which has a much wider range of values. Given that the quotient is small, its value may be estimated in many cases by looking at the first few digits of the values i*d, for the possible values of i, rather than by performing full comparisons. Example: d =567, q < 5.
So, if D = 1939, we know that, q=3 because D has leading digits 19 and so r = D - q*d = 238. However, if D commences with 17 we will have to consider more than two digits of D in order to distinguish between q=2 and q=3. Full comparisons will be needed to distinguish some cases unless d has other special properties, or unless complete accuracy in determining q is not required. 3 Constant divisor
3.1 Multiplication by the reciprocal of the divisor
Division by d (_0) may always be performed by multiplication by its reciprocal 1/d. Example:
This is the basis for division in computers such as the Cray 1 series where there is no division instruction. Rather, an instruction is provided that gives an approximation to the reciprocal. Division is performed using software to refine the reciprocal approximation to full precision and to multiply by the dividend [Iliffe 1982]. It is not a popular method for implementing division in hardware because repetitive methods are more facile. However, if there is a need to implement division by a particular constant then the reciprocal may be calculated once and for all in advance. Perhaps the most common use of division by a constant is in conversion
between number bases. There are two approaches, one which generates
the least significant digit first as the remainder from division by a
small constant - we will encounter that later. The other is to divide
by a large constant and generate the most significant digit
first. Suppose it is required to convert an n-bit binary number N into
a BCD decimal representation providing always the maximum number of
digits m, where Page 179 Example: Assume n=6 and m=2.
3.2 Direct calculation of the remainder for constant divisor
Calculation of D mod d, where d is a constant, can be performed by calculating D - (D*(1/d))*d, but this requires two multiplications. An alternative method is based on stored constants and properties of the modulus operation.
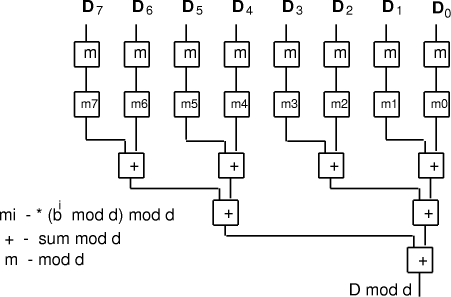
The constants E is in the limited range from 0 to n*d, so we can now use techniques
for small quotients to determine k so that (Fig. 2) shows an example for the case of n=8. Note that the additions, other than the last, may be carry-save so that the adder tree has similar cost and complexity to a multiplier. Page 180
Figure 2: Calculation of D mod d when d is constant A direct application of remaindering is range scaling for fixed-point
numbers. Many processes for calculating elementary functions require
that the argument be within a limited range, eg. 4 Small divisor
Small divisors are important in both theory and practice. If small is
taken to mean of length O(log n), then there are One use of small variables is in residue arithmetic [Szabo and Tanaka
1967]. In residue arithmetic, O(n/log n) distinct prime numbers For example (from [Beame, Cooke and Hoover 1986]), to calculate (D mod
d) mod m where D is n digits and m and d are O(log n) digits and d is
variable. Tables of the constants Page 181 to such a table given Under the same conditions, (D div d) mod m may be found using the
equivalence between mod and div. For A related trick is used in practice in ordinary full division or calculation of inverse. To start an iterative process going an approximation to the reciprocal of the divisor is needed. This may be looked up in a table using the first few bits of the divisor itself. This is used, for example, in the reciprocal approximation instruction in the Cray computers mentioned above [Iliffe 1982]. 5 Small constant divisor
When the divisor is both constant and small there are further possibilites for simplifying division. This fortuitous combination does occur in practice. A hardware application is with interleaved memory banks. If there are k banks then an address A may be located in bank A mod k at address A div k. Similar calculations are required at the software level if the size of data items packed into memory differs from the memory word size. Another application is in conversion between number bases. There are two directions that may be taken, one based on remaindering and the other on multiplication by reciprocals. 5.1 Division following derivation of remainders
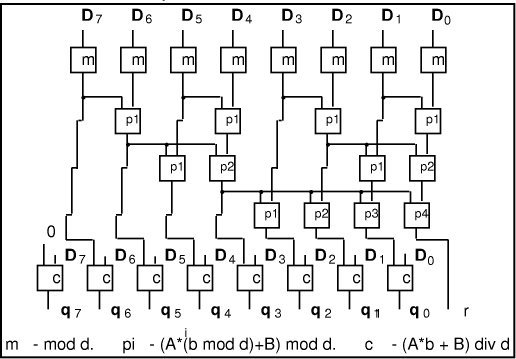
Figure 3. Remainder calculation for small divisor Here one applies the same technique as before for constant divisors,
but, because the divisor is also small, it is possible for all
additions to be perfromed modulo the divisor, keeping the intermediate
values small. The obvious circuit, (Fig. 3), calculates Page 182 d for
each digit, then finds Example:
Because the partial remainders are small, it is now reasonable to
calculate all in parallel and hence deduce the complete quotient. The
above approach has to be modified because the intermediate steps in
calculating D mod Example:
Figure 4: Derivation of quotient from remainders with small constant divisor 5.2 Multiplication by reciprocal
Page 183 The constant divisor may be factored into two constants as d = Divisor factor of number base The factor Concentrating on the ith digit:
The multiplier of Example:
Divisor relatively prime to number base Division by Example:
The additions may be performed in parallel in a tree-like structure but such a circuit is not much more simple than a general multiplier. However, with serial implementation Page 184 in firmware the technique has certainly been used in practice ([Jacobsohn 1973], [Artzy et. al. 1976]) in small computers. 6 Dividend exact multiple of divisor
Having a dividend D In the case of modular representation, if the inverse of X mod M
exists and if X = A situation where prior knowledge of the remainder can be helpful is
in calculating the quotient for small constant divisors that are
relatively prime to the number base. Suppose that we know the
remainder Example:
The value In [Artzy et. al. 1976] the following elegant version of reciprocal multiplication is given. Suppose d is relatively prime to the number base then, as before, 1/d
is a repeating base-b fraction Page 185 Example:
To convert this into a more practical procedure [Artzy et. al. 1976]
propose first restricting D to be < Example:
A practical use of division where it is known that d divides D exactly is where D is a, for example, byte offset previously constructed by multiplication of an offset q by the element size (in bytes) d. 7 Divisor related to the number base
We have encountered already some simplifying relationships between the divisor and number base. These included cases where the divisor divides the base exactly and where the divisor and the base are mutually prime. Another relationship of interest is when the divisor is close to the base in value. 7.1 Divisor close to number base in value
If the divisor is very close to the base, then it is possible to find the first digit of the quotient very quickly because it is the first digit of the dividend. This process may be continued and used to calculate the next quotient digit at each stage of the division process. The example below has the divisor close to the base but works with fixed point fractions. The same procedure may be applied to integer division where the divisor is close to some power of the base i.e. the same procedure with the point shifted to the right. Example:
This process is an important one that forms the basis of some of the fastest practical division algorithms [Ercegovac et. al. 1983] . Page 186 A case of particular interest is when the divisor is the constant b-1 or b+1. In fact, when the representation is binary many small integer divisors are in this form or are related to it. A binary number may be regarded as being base 4 (each digit of 2 bits), base 8 (each digit of 3 bits) etc. Division by 3 is by 4-1, by 5 4+1, by 7 8-1, by 9 8+1, by 17 16+1 etc 7.2 Division by Base-1
In this case remaindering is very simple. Because b = d+1, b mod d = 1
and so The reduction of the sum of digits mod d can be performed serially with the recurrence:
or can be calculated
with parallel tree circuits. If solely The calculation of the remainder mod b-1 is used in checking arithmetic in the classic 'casting out nines' procedure. For example, to check the full-sized multiplication A*B=C the relationship ((A mod d) * (B mod d)) mod d = C mod d is tested, where the multiplication is much simpler. In the manual approach the digits are not summed modularly digit by digit but rather they are summed using normal arithmetic and the process reapplied repeatedly until one digit remains: Example:
The same approach is used in computers for error checking. Usually, a binary number is regarded as being in base 4 and the remainder found mod 3. The digits 0, 1, 2 are kept in decoded form 100, 010, 001, to simplify the nodes in the tree circuit. Proceeding further, with the remainders known we can find the quotient
as in section 1.2 from
In words, the quotient digit i is the remainder adjusted by 1 if Page 187
Figure 5: Quotient from remainders for d = b-1 In the circuit of figure 5 there is some duplication of effort in that
the calculation of the final adjustment could well be associated with
the previous stage.This idea is used in the following serial algorithm
where the quotient is calculated as we proceed with determining the
partial remainders. This algorithm is particularly nice in that the
division is performed entirely by digit addition and comparison
Example: Division of a base 10 number by 9.
Note that it is also possible to calculate the remainders from right
to left. From Page 188 get If we knew 7.3 Division by Base+1
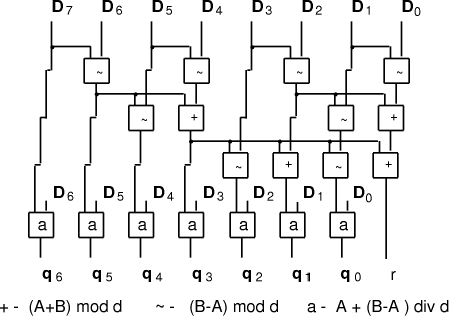
The above reasoning can be revisited with d = b+1. Noting that (A-B) mod d is the non-negative integer C such that (B+C) mod d = A mod d, in this case we find:
Without going into details, (Fig. 6) is an example circuit.
Figure 6: Quotient from remainders for d = b+1 And the serial version is (in standard arithmetic):
Example: Division of a base 10 number by 11: Page 189
Typical step:
The above two serial algorithms were described in [Doran 1987] though were presumably known to mental calculators previously. Surprisingly, division and remaindering by b+1 has had at least one practical2 application in the proposed Burroughs Scientific Processor of the 1970s which had 17 memory banks (b = 16). 7.4 Circuits with feedback
[Duke 1972] describes the circuit illustrated in (Fig. 7).
Figure 7: Duke's feedback division circuit This is unusual in that it is a logic circuit with feedback. If it ever produces a stable output then we must have:
If d divides D exactly then q = D div d. The question is, when is the output stable? This answer is clearly
technology and implementation dependent. In the case of binary
representation, the circuit will certainly work when '*(d-1)'
introduces a genuine shift. This is when d-1 = The above circuit can be adapted for d = Page 190 provides the correction factor to be added to each digit (also as described above for d = b-1). [Fenwick 1972] mentions that Boothroyd had proposed a similar circuit with feedback working from the most significant end. In this case, the shift is to the right. Unfortunately, because carry is to the left, this involves real feedback and cannot be guaranteed to stabilise. 7.5 Application to Binary to Decimal Conversion
We can at last see the practical use of division by a small constant for base conversion. The basic idea is that if we wish to convert a number D from a base b to a base d, then, because D = q*d+r, r is the zeroth digit of the representation base d. The process may then be applied to q to get the first digit, etc. If the arithmetic for the division is performed in base b, then the sequence of remainder digits are the representation in base d, with each digit represented in base b. Example:
The most common case is binary-to-decimal conversion which requires
division by 10. This may be performed by dividing the binary number by
5 then by 2. In both divisions the remainders are also found. If the
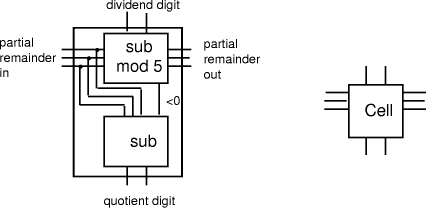
first division is D = 5*Q+ If conversion is required to be performed for one particular number then a tree division by b+1 circuit would be appropriate. Another technique, more appropriate for VLSI is to use a cellular circuit, where the approach is to use a network of idential components or cells that are connected in a two dimensional grid. Cellular binary-to-decimal circuits are explored in detail in [Schreiber and Stefanelli 1978]. To see an example, we could base a cellular circuit on our repetitive algorithm for b+1 division described above. The circuit consists of multiple levels, each performing a division by 10 and production of the next decimal digit encoded in BCD. The cell corresponds to the inner loop of the algorithm and performs a mod 5 subtraction of the incoming partial remainder (represented in 3 bits as being in range 0 to 4) with the next 2-bit digit of the binary number, followed by correction of the quotient digit based on the subtraction being negative (if it were not modular). Without fully developing the logic, the cell would be as in (Fig. 8). Page 191
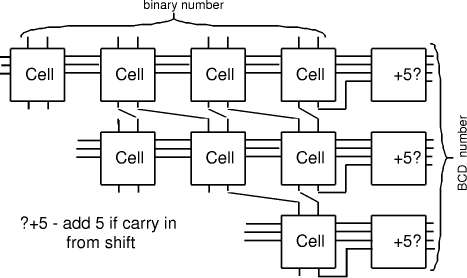
Figure 8: Cell for Binary to Decimal Conversion The cells are then combined into the grid, with division by 2 being performed by directing the wires to perform a shift. An array of special circuits on the right is needed to conditionally increment the digits by 5. Each level of division needs less circuitry. (Fig. 9) shows the example of 8-bit conversion (maximum value 255).
Figure 9: 8-bit cellular binary to decimal converter The circuit above is somewhat simpler than that presented in [Schreiber and Stefanelli 1978]. 8 Conclusion
There have certainly been many interesting procedures proposed for special cases of division. We have seen that these are mainly variations on two themes, division by reciprocal multiplication, or division derived from remaindering. Of course, for every specific constant divisor there are special tricks that can be brought to bear. These have been developed over the years by mental calculators, see [Aiken 1937] , [Menninger 1964], [Smith 1983], [Yang 1274] . This is a fascinating but endless pursuit that we will leave it to the reader to take further. Acknowledgments Page 192 This work was done while the author was a visitor with the Laboratoire d'Informatique du Parallelisme at the Ecole Normale Superieure at Lyon, France. Thanks is due to Jean-Michel Muller of LIP ENS and to Elena Calude and Radu Nicolescu of The University of Auckland for helpful suggestions. References
[Aiken 1937] Aiken, A. C.: 'Trial and error and approximation in arithmetic'; The Mathematical Gazette (1937), p. 117. [Alt and Blum 1983] Alt, H., Blum, N.: 'On the Boolean circuit depth of division and related functions'; Dept. of Computer Science, Pennsylvania State University (1983). [Artzy et. al. 1976] Artzy, E., Hinds, J. A., & Saal, H. J. : 'A fast division technique for constant divisors'; CACM, 19, 3 (1976), 98 - 101. [Beame, Cooke and Hoover 1986] Beame, P. W., Cook, S. A. & Hoover, H.J.:'Log depth circuits for division and related problems'; SIAM Journal on Computing, 15 (1986) 994-1003. [Cocke et. al. 1970] Cocke, J., Freiman C. V., & Homan M. E.: 'High speed division system'; US Patent # 3,527,930 (1970). [Daumas et. al. 1994] Daumas, M., Mazenc, C., Merrheim, X, and Muller, J-M.: 'Fast and Accurate Range reduction for thr computation of elementary functions'; 14th IMACS World Congree on Computational and Applied Mathemaatics, Atalanta, Georgia (1994). [Doran 1987] Doran, R. W.: 'Parallel division circuits for small divisors'; Tech Report No. 38. Department of Computer Science, University of Auckland (1987). [Duke 1972] Duke, K. A.: 'Division by small integers'; IBM Technical Disclosure Bulletin, 14, 9 (1972), 3736-2738. [Ercegovac et. al. 1993] Ercegovac, M.D., Lang, T., Montuschi, P.: 'Very high radix division with selection by rounding and prescaling'; Proceedings of the 11th Symposium on Computer Arithmetic, Windsor, Ontario (1993) 112 - 119. [Fenwick 1972] Fenwick, P.McA.: 'A binary representation for decimal numbers'; The Australian Computer Journal, 4, 4 (1972), 146 - 149. [Iliffe 1982] Iliffe, J. K.: 'Advanced Computer Design'; Prentice Hall. London (1982). [Jacobsohn 1973] Jacobsohn, D. H.: 'A combinatoric algorithm for fixed-integer divisors'; IEEE Transactions on Computers (1973), 608 - 610. [Menninger 1964] Menninger, K.: `Calculator's Cunning - The Art of Quick Reckoning'; G. Bell and Sons Ltd., London (1964). [Schreiber and Stefanelli 1978] Schreiber F. A., Stefanelli, R.: 'Two methods for fast integer binary-BCD conversion'; Proceedings of 4th Symposium on Computer Arithmetic, Santa Monica, California (1978), 200-207. [Smith 1983] Smith, S. B.: 'The Great Mental Calculators - The Psychology, Methods, and Lives of Calculating Prodigies Past and Present'; Columbia University Press, New York (1983). Page 193 [Szabo and Tanaka 1967] Szabo, N. S. & Tanaka, R. I.: 'Residue Arithmetic & its Applications to Computer Technology'; McGraw Hill, New York (1967). [Yang 1274] Yang Hui: 'Ch'eng Chu' T'ung Pien Suan Pao (Precious Reckoner for Variations of Multiplication and Division)'; Reprinted, translated with commentary, in Lam Lay Yong, A Critcal Study of the Yang Hui Suan Fa, Singapore University Press (1977). In [Beame, Cooke and Hoover 1986] this reduction is credited to [Alt and Blum 1983], but it appears to have been well understood by practitioners, and is used in, for example, [Cocke et. al. 1970]. 2 One could note in passing that in New Zealand the VAT (called GST) had been set at 10% initially then changed to 12.5%. To find the tax included in the purchase price the first rate needed division by 11 and the second by 9 - so these algorithms would have been useful, if we did not have calculators! Page 194
|
|||||||||||||||||
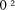 r < d.We will sometimes express q as D
div d and r as D mod d (r being often referred to as the residue
modulo d - remainder and modulo are sometimes defined differently for
signed numbers, but are the same for the non-negative integers with
which we are concerned here). Usually, the term division is restricted
to finding q, and the corresponding process of finding r as
remaindering.
r < d.We will sometimes express q as D
div d and r as D mod d (r being often referred to as the residue
modulo d - remainder and modulo are sometimes defined differently for
signed numbers, but are the same for the non-negative integers with
which we are concerned here). Usually, the term division is restricted
to finding q, and the corresponding process of finding r as
remaindering.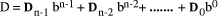
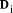 are the digits in the base b representation.
are the digits in the base b representation. 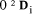 < b. The digits are uniquely determined.
< b. The digits are uniquely determined.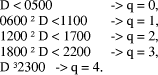 is the leading n-i digits of D regarded as an
integer. The
is the leading n-i digits of D regarded as an
integer. The 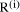 are called 'partial remainders'. The
are called 'partial remainders'. The 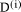 are each
represented as a subrange of the digits D. It is possible from D to
quickly make enough copies of its digits so as to represent all
are each
represented as a subrange of the digits D. It is possible from D to
quickly make enough copies of its digits so as to represent all 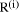 quickly.
quickly.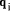 in order, commencing with the high order
in order, commencing with the high order 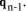 . At step i (i from n-1
down to 0) we divide d into the 'concatenation' of
. At step i (i from n-1
down to 0) we divide d into the 'concatenation' of 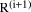 with the
next digit
with the
next digit 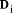 to find
to find 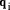 and
and 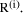 For example, in the following
'trace' of standard long division the partial remainders are picked
out in bold.
For example, in the following
'trace' of standard long division the partial remainders are picked
out in bold.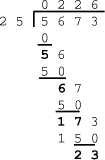
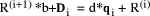 (assume that
(assume that  = 0). As we can find the
= 0). As we can find the  in
parallel quickly we can then determine the
in
parallel quickly we can then determine the 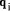 by dividing each
by dividing each 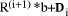 by d.
by d.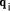 are less than b) - this is the special case that we
will cover first, below. However, here the situation is even more
special. From above, we have
are less than b) - this is the special case that we
will cover first, below. However, here the situation is even more
special. From above, we have 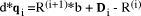 which can be
calculated quickly.
which can be
calculated quickly. 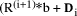 involves no calculation, it is
merely notation for concatenation. The subtraction of
involves no calculation, it is
merely notation for concatenation. The subtraction of 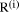 may be
performed quickly in a borrow lookahead circuit.)
may be
performed quickly in a borrow lookahead circuit.)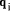 is in the range from 0 to b-1,
is in the range from 0 to b-1, 
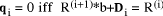 , in the case of binary division
, in the case of binary division 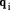 is fully determined by this comparison. *1
is fully determined by this comparison. *1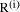 are known it is possible to determine
the
are known it is possible to determine
the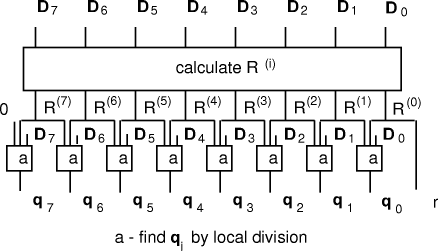
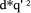 D < d*(q'+1).
D < d*(q'+1).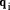 in turn from
in turn from 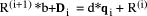 ,
i.e. by dividing d into
,
i.e. by dividing d into 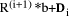 to find the quotient
to find the quotient 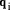 that we
know is < b. Using the same data as above:
that we
know is < b. Using the same data as above: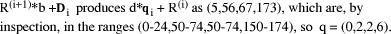
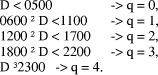
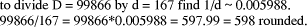
 . Firstly, N can be divided by
. Firstly, N can be divided by 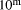 (in
binary) then the quotient multiplied successively by 10 (in binary,
multiplication by a small constant can, of course, be performed by a
sequence of additions and shifts), collecting 4-bit decimal BCD digits
as they appear to the left of the binary point. Division by
(in
binary) then the quotient multiplied successively by 10 (in binary,
multiplication by a small constant can, of course, be performed by a
sequence of additions and shifts), collecting 4-bit decimal BCD digits
as they appear to the left of the binary point. Division by 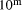 can be
performed by multiplying by
can be
performed by multiplying by 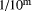 (kept with sufficient precision to
convert the largest binary integer).
(kept with sufficient precision to
convert the largest binary integer).
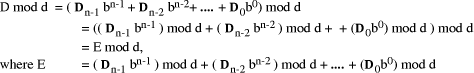
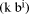 mod d
mod d 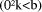 can be stored in n tables with b
entries of n digits,
can be stored in n tables with b
entries of n digits, 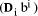 mod d selected by table look up, and
then E found as the sum. The addition can be performed in software,
or, in hardware, in logarithmic time using a tree of adders.
mod d selected by table look up, and
then E found as the sum. The addition can be performed in software,
or, in hardware, in logarithmic time using a tree of adders.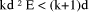 . D mod d, =
E mod d, is then E - kd. This can again be performed in software or, if speed is of essence, in hardware by comparing E in parallel with all the constants i*d.
. D mod d, =
E mod d, is then E - kd. This can again be performed in software or, if speed is of essence, in hardware by comparing E in parallel with all the constants i*d.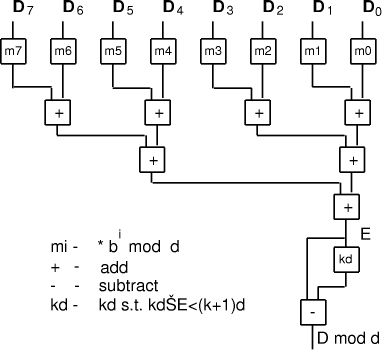
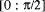 for sin. To
calculate sin(x) it is necessary to reduce the range of x by
determining x mod
for sin. To
calculate sin(x) it is necessary to reduce the range of x by
determining x mod 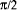 . It is possible to make the final 'small
quotient' step fast, using only a small table look-up, if, as is often
the case, the actual range of convergence is somewhat wider than the
target range [
. It is possible to make the final 'small
quotient' step fast, using only a small table look-up, if, as is often
the case, the actual range of convergence is somewhat wider than the
target range [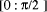 to
to 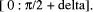
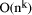 different
numbers representable. Dealing with a variable integer of length O(log
n) is thus the same as considering
different
numbers representable. Dealing with a variable integer of length O(log
n) is thus the same as considering 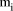 each of length O(log n) are chosen. A number X of length O(n) is then
represented by the small numbers
each of length O(log n) are chosen. A number X of length O(n) is then
represented by the small numbers 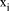 where
where 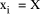
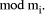 The
advantage of this system is that (X op Y) mod M is performed, for many
op, as
The
advantage of this system is that (X op Y) mod M is performed, for many
op, as 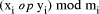 in parallel. Unfortunately, division is, in
general, not in this category. Regardless of the benefit of this
approach it leads to interest in operations on numbers of length O(log n).
in parallel. Unfortunately, division is, in
general, not in this category. Regardless of the benefit of this
approach it leads to interest in operations on numbers of length O(log n).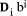 mod d for every possible
mod d for every possible 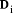 and d have size
and d have size 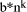 for each i. Reference
for each i. Reference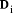 and d takes time log
and d takes time log 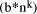 = O(log n). Thus, the direct calculation
approach for determining D mod d given above for constant d may be
used with variable small d to also give a O(log n) algorithm.
= O(log n). Thus, the direct calculation
approach for determining D mod d given above for constant d may be
used with variable small d to also give a O(log n) algorithm.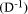 mod m (where
mod m (where 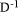 is defined
as the integer < m such that
is defined
as the integer < m such that 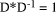 mod m), we may compute y = D
mod m and then look up
mod m), we may compute y = D
mod m and then look up 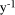 in a table of size
in a table of size 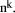
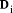 mod
mod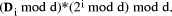 At each level of
the adder tree, addition mod d is performed.
At each level of
the adder tree, addition mod d is performed.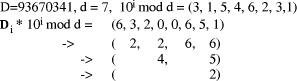
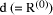 do not help in finding the other partial
remainders
do not help in finding the other partial
remainders 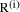 . A clever procedure [
. A clever procedure [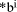 mod d step and do the reduction addition as
mod d step and do the reduction addition as 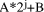 mod d
steps, thus spreading the '
mod d
steps, thus spreading the ' 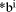 ' operation over multiple stages. This
gives the approach shown for n=8 in (Fig. 4), refining the circuit of (Fig. 1).
' operation over multiple stages. This
gives the approach shown for n=8 in (Fig. 4), refining the circuit of (Fig. 1).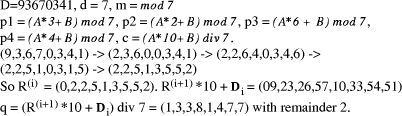
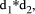 where
where 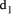 has prime factors that are also factors of the number base b and where
has prime factors that are also factors of the number base b and where 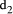 is relatively prime to b. Division by d can be performed by successive division by
is relatively prime to b. Division by d can be performed by successive division by 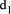 and
and 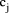 such that
such that 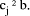 Division by
Division by 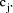
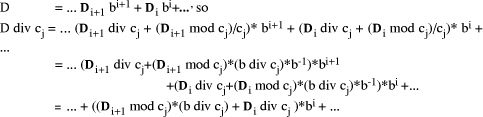
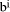 in this expression =
in this expression = 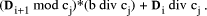 This is non-negative and has maximum value of
This is non-negative and has maximum value of 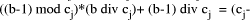
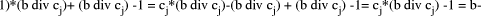
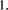 Thus the expression above represents the unique representation base b of D
div
Thus the expression above represents the unique representation base b of D
div 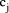 . The value of each digit is found from the local expressions
. The value of each digit is found from the local expressions
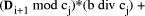
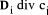 which may be calculated in
parallel. That is, division by prime factor of the number base is
essentially a trivial operation on digit-size numbers. In particular,
of course, if
which may be calculated in
parallel. That is, division by prime factor of the number base is
essentially a trivial operation on digit-size numbers. In particular,
of course, if 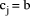 then the ith digit is
then the ith digit is 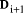 - division reduces to
shifting.
- division reduces to
shifting.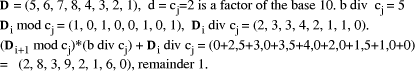
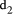 is more of a challenge and must, in general, be
performed by multiplication by the reciprocal. However, because
is more of a challenge and must, in general, be
performed by multiplication by the reciprocal. However, because 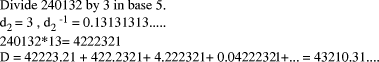
 that is an exact multiple of the divisor d
does not really simplify the division process for standard
representations because it is certainly not the case that d divides
the other
that is an exact multiple of the divisor d
does not really simplify the division process for standard
representations because it is certainly not the case that d divides
the other  exactly. However, it can be a help in special cases and
with other representations.
exactly. However, it can be a help in special cases and
with other representations. then the representation of
then the representation of 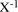 mod M
is
mod M
is 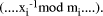 If Y=kX mod M then
If Y=kX mod M then 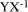 mod M is Y div X and
is represented by
mod M is Y div X and
is represented by 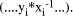 In other words, exact division
works precisely as expected in modular representation. Unfortunately,
if
In other words, exact division
works precisely as expected in modular representation. Unfortunately,
if 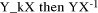 mod M has no obvious relationship to Y div X, nor is
there an obvious means of calculating quickly (Y div X )mod M.
mod M has no obvious relationship to Y div X, nor is
there an obvious means of calculating quickly (Y div X )mod M.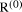 , then
, then 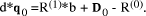 If d and b are
relatively prime there is only one k for which kb +
If d and b are
relatively prime there is only one k for which kb + 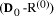 is a
multiple of d by a factor less than b. We can thus deduce both
is a
multiple of d by a factor less than b. We can thus deduce both 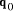 and
and 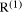 . Having found
. Having found 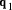
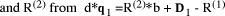 , and so on. Thus it becomes possible to calculate
the quotient, and partial remainders, from least significant digit
first.
, and so on. Thus it becomes possible to calculate
the quotient, and partial remainders, from least significant digit
first.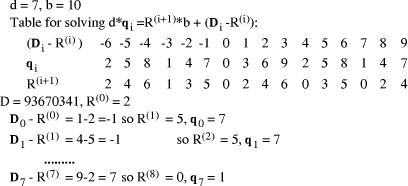
 is a check on errors in our calculation because
is a check on errors in our calculation because  was correct. If the remainder
was correct. If the remainder  = 0.
= 0.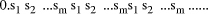 If
If 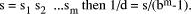 Now, suppose that D =
qd is an exact multiple of d, then D*s = q*d*s = q*
Now, suppose that D =
qd is an exact multiple of d, then D*s = q*d*s = q* 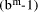 = q*
= q* 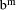 -
q. So, if q <
-
q. So, if q < 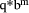 has low-order m digits zero).
has low-order m digits zero).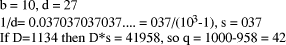
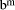 , in which case q <
, in which case q < 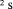 only if d divides D exactly, so
the error of d not dividing D exactly can be detected. If
only if d divides D exactly, so
the error of d not dividing D exactly can be detected. If 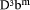 then
the technique is extended to use ss of length 2m, then ssss of length
4m etc., until D is within range, looking at the last 2m, 4m etc
digits of D*ss, D*ssss etc. Multiplication by ss, ssss etc. is
performed as *s*( +1), *s*( +1)*(b2m+1) etc. (multiplication by
bkm+1, is, of course, shift and add).
then
the technique is extended to use ss of length 2m, then ssss of length
4m etc., until D is within range, looking at the last 2m, 4m etc
digits of D*ss, D*ssss etc. Multiplication by ss, ssss etc. is
performed as *s*( +1), *s*( +1)*(b2m+1) etc. (multiplication by
bkm+1, is, of course, shift and add).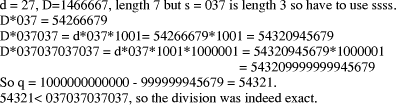
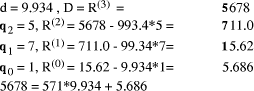
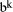 mod d =1. Hence
mod d =1. Hence 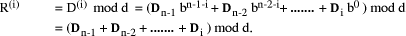
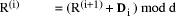
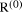 is required then one can
use a tree circuits as in (Fig. 2). If all
is required then one can
use a tree circuits as in (Fig. 2). If all 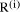 are required a circuit
as in the top part of (Fig. 5) is appropriate.
are required a circuit
as in the top part of (Fig. 5) is appropriate.
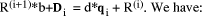
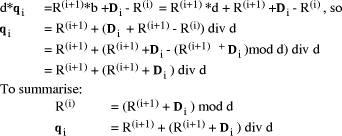
 d. This correction may be applied in parallel as a single
step as in (Fig. 5) for n=8.
d. This correction may be applied in parallel as a single
step as in (Fig. 5) for n=8.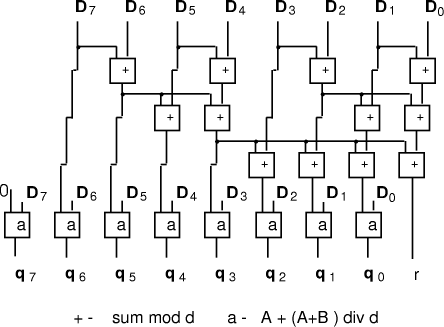
 d
(in the algorithm all arithmetic is standard).
d
(in the algorithm all arithmetic is standard).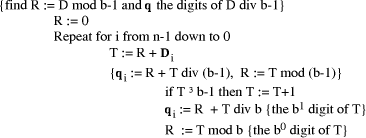

 =
=  mod d, we find
mod d, we find  mod d. Continuing this expansion we
mod d. Continuing this expansion we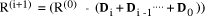 mod d. Finally,
mod d. Finally, 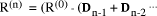
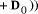 mod d.
mod d.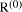 correctly then we would have
correctly then we would have 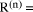 0. However, if we
did not know
0. However, if we
did not know 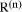 but assumed it zero then we will have
but assumed it zero then we will have 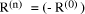 mod d. The remainders that we have found will be incorrect but they
can be restored by now adding
mod d. The remainders that we have found will be incorrect but they
can be restored by now adding 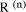 mod d. This approach is inherent
in the circuit of [
mod d. This approach is inherent
in the circuit of [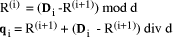
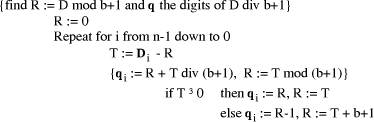

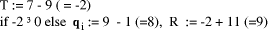
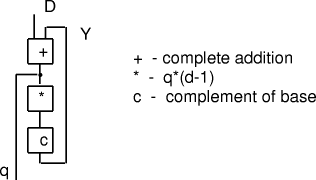
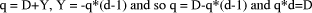
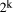 , so d =
, so d = 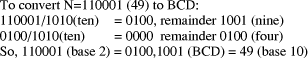
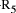 and the second is Q = 2*q +
and the second is Q = 2*q + 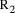 , the
combined effect is D = 5*(2*q+
, the
combined effect is D = 5*(2*q+ 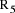 = 10*q + (5*
= 10*q + (5* 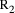 is 0 or 1, the remainder mod 5 is increased by 5 if the
remainder mod 2 is 1, to give the remainder mod 10 which is the next
decimal digit. Because 5 =
is 0 or 1, the remainder mod 5 is increased by 5 if the
remainder mod 2 is 1, to give the remainder mod 10 which is the next
decimal digit. Because 5 = 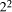 +1, we can regard the binary number as
being base b=4 and use our circuits for division by b+1, and the
division by 2 is, of course, a shift to the right.
+1, we can regard the binary number as
being base b=4 and use our circuits for division by b+1, and the
division by 2 is, of course, a shift to the right.