| Submission Procedure |
On Implementing EREW Work-Optimally on Mesh of Trees
(University of Turku, Finland Ville.Leppanen@cs.utu.fi) Abstract: We show how to implement an Key Words: EREW, mesh of trees, shared memory, simulation, work-optimal, randomized, coated mesh. Category: C.1.2 C.2.1 F.1.2 F.2.2 G.3. 1 Introduction
PRAM is an abstract model of parallel computation. It consists of p processors and a single shared memory of size m. The shared memory concept of the PRAM is generally believed not to be directly implementable as an extension of the conventional memory technique to the p-port memory technique (this does not seem to hold for relatively small p [Forsell 93]). Therefore, the implementation of PRAM is usually considered on distributed memory machines (DMMs), where processor memory pairs are connected by some interconnection network [Abolhassan et al. 91][Karp et al. 92][Leppaenen and Penttonen 94a] [Ranade 91][Valiant 90]. Simulation of PRAM on a 2-dimensional Mesh of
Trees (MT) based DMM has been considered previously in [Luccio et
al. 88][Pucci 93] probabilistically and in [Luccio et al. 90][Pucci
93] deterministically. The probabilistic simulation of an n-processor
EREW PRAM on an n-processor In this paper, we show how to decrease the work per simulated processor to O(1) with high probability. We prove this result for both 2-dimensional and 3-dimensional MTs. The method is, of course, increasing the multithreading level of each processor so that the cost caused by routing delay decreases - i. e., we make each of the N real processors to simulate p/N EREW processors, and require that the number of PRAM processors p is sufficiently large. In our simulations, Page 23 we implement each virtual processor as a light-weight thread (= fixed set of registers). For ease of reference, we call the multithreading level of processors simply by load, and increasing the load by overloading. The work-optimality of our simulations can be questioned,
since the number of MT-nodes is Next, we give some necessary definitions [Section 2], and describe workoptimal EREW PRAM simulation on 2-dimensional and 3-dimensional mesh of trees [Section 3]. Then, we give experimental EREW simulation results [Section 4], and compare [Section 5] the MT results to those obtained for similar work-optimal simulations on coated meshes [Leppaenen and Penttonen 94b]. We conclude [Section 6] by proposing some topics for further research. 2 Definitions
2.1 EREW PRAM
Definition 1. EREW (Exclusive-Read-Exclusive-Write) PRAM model
consists of p processors and a shared memory M of size m. Each of the
processors 2.2 Mesh of Trees
Definition 2. An n-sided d-dimensional Mesh of Trees (MT) is a graph,
which is based on an n-sided d-dimensional mesh of nodes (without grid
edges). For each tower of mesh nodes In the 2-dimensional case [see Fig. 1], we call Page 24 reside at the
root of Fig. 1. A 2-dimensional 4-sided mesh of trees. 3 Simulation
Initially, the shared memory is hashed according to some randomly
chosen hash function
Page 25 where q is a prime and Lemma 3. [Kruskal et al. 90], Corollary 4.20. If a randomly chosen
where 3.1 2-dimensional Mesh of Trees
In the 2-dimensional case, the routing is straightforward, since the
processors are on the roots of row trees and the memory modules are on
the roots of column trees. In fact, the path from Theorem 4. For properly chosen (small) constants k and l, there exists
such a constant Proof. We assume that each processor simulates
Page 26
for some positive constant The
queues do not need to be infinite. If How do we know, when to start simulating the next EREW step? We could assume that we first check whether all processors have received all replies. However, we do not actually need such a global control, if we proceed in the following way. Assume that after the last memory reference packet, each processor sends an End-Of-Stream packet. The row tree nodes can spread this EOS-packet to both branches, and respectively the column tree nodes let all other packets go before they combine two EOS-packets, and forward the result upwards. Now, each memory module knows when it has issued the last reply, and can thus send an End-of-Replies packet. Assume that the EOR-packets are transferred in the same way as the EOS-packets. Clearly, each processor can start simulating the next step, when it has received an EOR-packet. In principle, a processor could start simulating the next round right after it has injected its EOS-packet. However, in practice this can cause problems with the coordination of virtual processors. Acting like this, the simulation of at most two consecutive EREW steps are overlapped, but never mixed. As in [Luccio
et al. 88][Pucci 93], we can protect ourselves against some repeatedly
occuring bad memory reference patterns, by requiring that the whole
shared memory is rehashed, ifsome memory module receives more than
cxllog n packets for a carefully chosen constant c. Clearly, a memory
of size 3.2 3-dimensional Mesh of Trees
To extend the result of Theorem 4 to the 3-dimensional mesh of trees,
we only need to describe how to route the packets, and how to keep the
simulation of two consecutive PRAM steps separated. Using Lemma 3, it
is again easy to prove that each memory module Let us again call those trees,
where the processors and the memory modules are connected, the row and
the column trees respectively. Let depth tree Page 27 and down to mesh node Can
we guarantee that there is no congestion in the depth tree nodes? A
read or a write packet entering to a depth tree
for some constant As in the 2-dimensional case, we can keep the simulation of consecutive steps separate by sending EOS- and EOR-packets. However, we must require that when they traverse the depth trees, they always go via the root. Based on the above discussion, we have Theorem 5. Theorem 5.
For properly chosen (small) constants k and l, there exists
such a constant 3.3 Practical Remarks
It is straightforward to extend the EREW simulation result to higher dimensional mesh of trees. However, finding an efficient layout for d-dimensional (d > 3) mesh of trees is obviously very difficult, if not impossible. We did not pay much attention to the impracticality of
family
is so huge that it is not necessary to guarantee success with high
probability for all of them. After all, what is wanted is that in the
long run the average simulation time of one PRAM step is Although the rehashing method proposed earlier in this paper is sufficiently good for asymptotic complexity results, it is likely to be too 'rough' in practice. Undoubtly, it is good to have a rehashing mechanism, but its triggering criteria should be chosen very carefully. We believe that one should make the decision on the basis of a long (bad) simulation sequence. Page 28 If we ignore the effect of rehashing on the expected routing cost per PRAM processor, by [Section 3.1] and [Section 3.2], we know that the cost is at most
in the 2-dimensional case and 4 Experimental Results
Full details of our routing experiments on the mesh of trees are documented in [Leppaenen 94b]. Here, we only give an overview of the test setting and the results. The integration of processors and the
memory modules to the mesh of trees based routing machinery is as
described before. We assume that the processors and the routing
machinery nodes can send and receive at most one packet in one time
unit. We assume that the memory modules can generate a reply in one
time unit, and there is a FIFO queue of a fixed length We did not use We made about 30 experiments
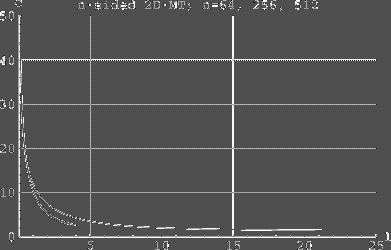
with each chosen parameter combination. Altogether about 2400 routing
experiments were conducted on 2-dimensional 64, 256-, and
512-processor -MTs [see Fig. 2], and on 3-dimensional 256-, 1024-, and
4096-processor MTs [see Fig. 3]. We measured only the time to complete
a single experiment - as mentioned earlier, overlapping of consecutive
steps is likely to decrease the total simulation cost. In each case,
the variation ofrouting times was small. The curves describing our
experiments show the dependency of simulation cost c (average
simulation time per Load) as a function of We see that for 2D MT sizes 64, 256 and 512, value In the 3-dimensional case, we found out
that value Page 29
Fig. 2. The simulation cost as a function of l in 2D MT. The highest
and at the same time the longest of the curves represents a 2D MT of
size 64. The next highest (and longest) curve corresponds to a
256-processor 2D MT, and the lowest curve represents a 512-processor
2D MT. The Y-axis shows simulation cost c per simulated processor (in
terms of routing steps per simulated processor), and the X-axis shows
the load as a function of l, where
Fig. 3. The simulation cost as a function of l in 3D MT. The highest and at the same time the longest of the curves represents 3D MT of size 256 processors. The next highest (and longest) curve corresponds to a 1024-processor 3D MT, and the lowest curve represents a 4096-processor 3D MT. Page 30 5 Comparison with Coated Mesh
As observed, the simulation cost is very small for the 2-dimensional and 3dimensional mesh of trees. However, other parameters of EREW PRAM implementations are also important. In the following, we present a comparison with the simulation cost on the coated meshes [Leppaenen and Penttonen 94b].
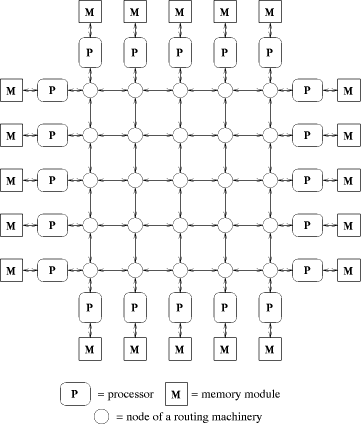
Fig. 4. A 2-dimensional coated mesh with 20 processors. A coated mesh [see Fig. 4] consists of a mesh connected routing
machinery coated with processor memory pairs. Both the coated mesh and
the mesh of trees have a routing machinery of size Page 31 to further improve the simulations both cases. We feel that the distance between neighboring nodes is important, since it might limit the clockrate of the routing machinery. So far, increasing the clockrate has been a major source of perforÈmance improvements. For the coated mesh structure, we use the experimental results documented in [Leppaenen 93][Leppaenen 94a].
Table 1. Mesh of Trees versus Coated Mesh. N is the number of real processors in each case. Distance tells the lower bound for the minimum (physical) distance between two logical neighbors (measured in routing machinery nodes). To our knowledge, no layout achieving the lower bound is known. Cost tells the simulation cost on a given Load. The two rightmost columns compare the two PRAM implementations with N processors. An emphasized number x means that MT is x times better than CM in this respect. Respectively, plain x means that CM is x times better. In [Tab. 1], we have chosen two load values for both comparisons. In all cases, the simulation cost depends on the available load in a very similar way. The load values of MT and CM are chosen from similar positions of the load-cost dependency curves [Leppaenen 94b] [Leppaenen and Penttonen 94b]. Especially, we attempted to choose the measure points so that the relative position on the MT curve and on the corresponding CM curve is the same. The first values are chosen from an area, where the load-cost curve begins to show asymptotic behavior, and the second values are chosen from an area were the behavior is asymptotic. The mesh of trees is clearly better [Tab. 1] in terms ofthe simulation cost and the load in the 2-dimensional case. In the 3-dimensional case, the mesh of trees is only slightly better in this respect. Moreover, the routing machinery nodes are a little bit simpler in the mesh of trees (less inputs and outputs). However, what is gained in the simulation cost and in the required load, is lost in the size of the routing machinery and in the distance between routing machinery nodes. Especially, in the 3-dimensional case it seems that the coated mesh is actually Page 32 better than the mesh of trees. A 6 Conclusions and Future Work
We have presented a work-optimal EREW PRAM implementation for the 2-dimensional and 3-dimensional mesh of trees. The simulation uses a novel technique to keep the simulation of consecutive PRAM steps separated. Although the proved simulation costs are small, our experiments show the real simulation costs to be about 2-3 times smaller in practice. We compared the properties of the presented simulations to those proposed for the 2-dimensional and 3-dimensional coated meshes. Neither a mesh of trees nor a coated mesh is strictly better than the other, but our conclusion is that in the 3-dimensional case the coated mesh is better, when all the mentioned properties are considered. We would like to learn more about the hardware complexity of the routing machinery nodes, and the ability to fast support a large number of virtual processors (how large systolic register set arrays can be built). It would also be interesting to compare these EREW PRAM simulations to those proposed for other logarithmic networks. Extending our work-optimal EREW simulation to an efficient work-optimal CRCW simulation is also an open problem. References
[Abolhassan et al. 91] Abolhassan, F., Keller, J., Paul, W.J.: 'On the Cost-Effectiveness of PRAMs'; Proc. 3rd IEEE Symposium on Parallel and Distributed -Computing, ACM Special Interest Group on Computer Architecture, and IEEE Computer Society (1991), 2 - 9. [Engelmann and Keller 93] Engelmann, C., Keller, J.: 'Simulation-Based Comparison of Hash Functions for Emulated Shared Memory'; Proc. PARLE'93 Parallel Architectures and Languages Europe, Springer, LNCS 694 (1993), 1 - 11. [Forsell 93] Forsell, M.J.: 'Are Multiport Memories Physically Feasible?'; Technical -Report A-1993-1, University of Joensuu, Department of Computer Science (1993). [Karp et al. 92] Karp, R.M., Luby, M., Meyer aufder Heide, F.: 'Efficient PRAM Simpulation on a -Distributed Memory Machine'; Proc. 24th Annual ACM Sympo@sium on -Theory of Computing (1992), 318 - 326. [Kruskal et al. 90] Kruskal, C.P., Rudolph, L., Snir, M.: 'A Complexity Theory of Efficient Parallel Algorithms'; Theoretical Computer Science, 71 (1990), 95è132. [Leppaenen 93] Leppaenen, V.: 'PRAM Computation on Mesh Structures'; Technical Report R-93-9, University of Turku, Computer Science Department (1993). Ph.Lic. thesis. Page 33 [Leppaenen 94a] Leppaenen, V.: 'Performance of Four Work-Optimal PRAM Simulation Algorithms on Coated Meshes'; Manuscript (1994), submitted for publication. [Leppaenen 94b] Leppaenen, V.: 'Experimental Results on Simulating EREW PRAM Work-Optimally on Mesh of Trees'; Technical Report R-94-10, University of Turku, Computer Science Department (1994), also appeared as electronic version, anonymous -FTP cs.utu.fi, in pub/techreports/1994/R-94-10.ps.Z. [Leppaenen and Penttonen 94a] Leppaenen, V., Penttonen, M.: 'Simulation of PRAM Models on Meshes'; Proc. PARLE'94 Parallel Architectures and Languages Europe, -LNCS 817 (1994), 146 - 158. [Leppaenen and Penttonen 94b] Leppaenen, V., Penttonen, M.: 'Work-Optimal Simulation of PRAM Models on Meshes'; Technical Report R-94-1, University of Turku, Computer Science Department (1994), submitted for publication. [Luccio et al. 88] Luccio, F., Pietracaprina, A., Pucci, G.: 'A Probabilistic Simulation of PRAMs on a Bounded Degree Networks'; Information Processing Letters, 28 (1988), 141-147. [Luccio et al. 90] Luccio, F., Pietracaprina, A., Pucci, G.: 'A New Scheme for the Deterministic Simulation of PRAMs in VLSI'; Algorithmica, 5, 4 (1990), 529 - 544. [Pucci 93] Pucci, G.: 'Parallel Computational Models and Data Structures'; Technical Report TD-13/93, PhD thesis, Dipartimento di Informatica, Universita' di Pisa - Genova - Udine, Italia (1993). [Ranade 91] Ranade, A.G.: 'How to Emulate Shared Memory'; Journal of Computer and System Sciences, 42 (1991), 307-326. [Valiant 90] Valiant, L.G.: 'General Purpose Parallel Architectures'; Algorithms and Complexity, Handbook of Theoretical Computer Science A (1990), 934-971. Acknowledgements The author would like to thank Martti Penttonen for guidance and helpful comments. This work was possible due to a grant provided by the computer science department of the University of Turku. Page 34
|
|||||||||||||||||
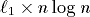 -processor EREW PRAM
workoptimally on a 2-dimensional n-sided mesh of trees, consisting of
n processors, n memory modules, and
-processor EREW PRAM
workoptimally on a 2-dimensional n-sided mesh of trees, consisting of
n processors, n memory modules, and 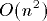 nodes. Similarly, we prove
that an
nodes. Similarly, we prove
that an 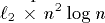 -processor EREW PRAM can be implemented
work-optimally on a 3-dimensional n-sided mesh of trees. By the
work-optimality of implementations we mean that the expected routing
time of PRAM memory requests is
-processor EREW PRAM can be implemented
work-optimally on a 3-dimensional n-sided mesh of trees. By the
work-optimality of implementations we mean that the expected routing
time of PRAM memory requests is 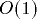 per simulated PRAM processor
with high probability. Experiments show that on relatively small
per simulated PRAM processor
with high probability. Experiments show that on relatively small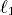 and
and 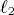 the cost per simulated PRAM processor is 1.5-2.5 in the
2-dimensional case, and 2-3 in the 3-dimensional case. If at each step
at most 1/3'th of the PRAM processors make a reference to the shared
memory, then the simulation cost is approximately 1. We also compare
our work-optimal simulations to those proposed for coated meshes.
the cost per simulated PRAM processor is 1.5-2.5 in the
2-dimensional case, and 2-3 in the 3-dimensional case. If at each step
at most 1/3'th of the PRAM processors make a reference to the shared
memory, then the simulation cost is approximately 1. We also compare
our work-optimal simulations to those proposed for coated meshes. 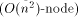 MT is proved to work in time
MT is proved to work in time
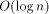 with high probability. The deterministic scheme is
respectively proved to work in time
with high probability. The deterministic scheme is
respectively proved to work in time 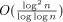 . Thus, the work per
simulated PRAM processor is and
. Thus, the work per
simulated PRAM processor is and 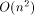 (or
(or 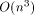 in the 3-dimensional
case) while the number of real processors is only O(n) (respectively
in the 3-dimensional
case) while the number of real processors is only O(n) (respectively
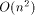 ). We adopt the approach taken by Valiant in [
). We adopt the approach taken by Valiant in [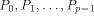 has some local memory and
registers. During one step a PRAM processor can either do a local
operation, read a shared memory location, or write to a shared memory
location. The phases of each step are executed synchronously, and the
next step is not started until all processors have finished the
current one. The EREW PRAM does not allow concurrent reading or
concurrent writing of a shared memory location. However, a shared
memory location may be read and written during the same step. A read
operation returns the value of the memory location in question before
the current step.)
has some local memory and
registers. During one step a PRAM processor can either do a local
operation, read a shared memory location, or write to a shared memory
location. The phases of each step are executed synchronously, and the
next step is not started until all processors have finished the
current one. The EREW PRAM does not allow concurrent reading or
concurrent writing of a shared memory location. However, a shared
memory location may be read and written during the same step. A read
operation returns the value of the memory location in question before
the current step.)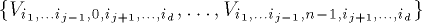 , it contains a complete binary tree
, it contains a complete binary tree
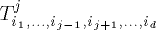 whose leaves are the nodes of the
tower. The edges of complete binary trees are bi-directional, and have
a queue of length q packets for both directions. The MT contains no
other edges. The degree of MT is max(3, d), and the number of nodes is
whose leaves are the nodes of the
tower. The edges of complete binary trees are bi-directional, and have
a queue of length q packets for both directions. The MT contains no
other edges. The degree of MT is max(3, d), and the number of nodes is
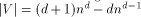 . Respectively, the diameter is
. Respectively, the diameter is 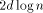 .
.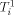 the i'th row tree
the i'th row tree
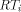 , and
, and 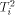 the i'th column tree
the i'th column tree 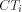 . In [
. In [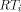 and
and 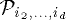 is in the root of
is in the root of 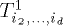 for each
for each 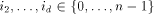 . Similarly, we assume memory module
. Similarly, we assume memory module 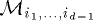 to
to 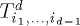 . Thus, the n-sided d-dimensional mesh of trees
consists of
. Thus, the n-sided d-dimensional mesh of trees
consists of 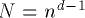 processors and memory modules.
processors and memory modules.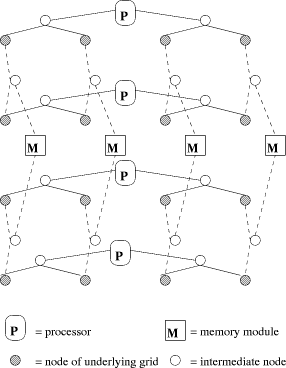
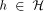 . Memory references are translated to read
and write packets, which are routed to the memory module on whose
custody the referenced shared memory cell is. Each packet is routed
along the obvious route as in [
. Memory references are translated to read
and write packets, which are routed to the memory module on whose
custody the referenced shared memory cell is. Each packet is routed
along the obvious route as in [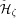 of
polynomial hash functions.
of
polynomial hash functions.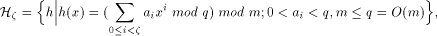
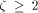 . The family
. The family 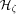 is not the best
possible, because we would like to define mappings owner:
is not the best
possible, because we would like to define mappings owner: 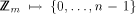 and location:
and location: 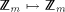 , by
, by 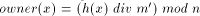 , and
, and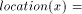
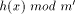 . This does not work in practice,
since a randomly chosen
. This does not work in practice,
since a randomly chosen 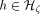 is not bijective. However, the secondary hashing techniques within memory modules (as in [
is not bijective. However, the secondary hashing techniques within memory modules (as in [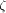 ), but if processors have a certain
pipeline of length O(
), but if processors have a certain
pipeline of length O(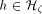 is used for hashing a set S of unique memory locations into n
modules, for which
is used for hashing a set S of unique memory locations into n
modules, for which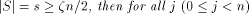 , :
, :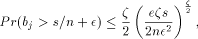
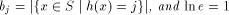 .
.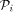 to
to 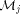 via mesh
node (i, j) is unique. Moreover, if q is sufficiently large, no
collisions can happen, when read and write packets traverse 'own'
along row trees, or when replies traverse down along column
trees. Collision, and thus queuing, happens only, when replies
traverse 'up' along row trees, or read and write packets traverse up
along column trees. If s packets are destined to some memory module
via mesh
node (i, j) is unique. Moreover, if q is sufficiently large, no
collisions can happen, when read and write packets traverse 'own'
along row trees, or when replies traverse down along column
trees. Collision, and thus queuing, happens only, when replies
traverse 'up' along row trees, or read and write packets traverse up
along column trees. If s packets are destined to some memory module
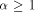 that a 2-dimensional n-processor MT with
that a 2-dimensional n-processor MT with
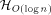 addressing and
addressing and 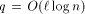 can simulate an -processor EREW PRAM workoptimally in
can simulate an -processor EREW PRAM workoptimally in 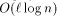 expected routing
steps with probability at least
expected routing
steps with probability at least 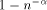 , if
, if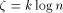 and
and 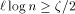 .
.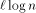 EREW processors. For the time being, assume that
EREW processors. For the time being, assume that 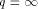 . According to
Lemma 3
. According to
Lemma 3 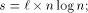
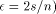
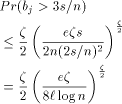
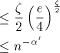
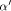 , if
, if 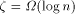 . Since
. Since 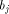 tells how many requests memory module
tells how many requests memory module 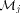 receives at most with high
probability, we know that every request reaches its destination in
receives at most with high
probability, we know that every request reaches its destination in 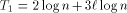 steps with probability at least
steps with probability at least 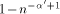 . Routing
the packets back is easier, since each processor receives at most
. Routing
the packets back is easier, since each processor receives at most 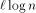 replies. Thus, the last reply is received at most
replies. Thus, the last reply is received at most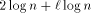 steps after some memory module received the last read request.
steps after some memory module received the last read request.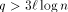 , then according to
the above reasoning none of the queues becomes full with high
probability. Thus, setting
, then according to
the above reasoning none of the queues becomes full with high
probability. Thus, setting 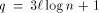 guarantees that the queue
length will not affect the routing time with high probability.
guarantees that the queue
length will not affect the routing time with high probability.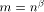 can certainly be redistributed in time
can certainly be redistributed in time 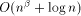 .
By now we know that if
.
By now we know that if 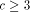 , the redistribution takes place at
most with probability
, the redistribution takes place at
most with probability 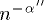 . Thus, if
. Thus, if 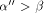 , the effecton the expected number of routing steps is negligible.
, the effecton the expected number of routing steps is negligible.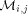 receives at most
receives at most
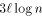 packets with high probability.
packets with high probability.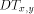 denote tree
denote tree
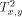 . Now, a packet is sent from processor
. Now, a packet is sent from processor 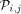 to memory module
to memory module 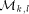 so that the packet goes along
so that the packet goes along 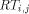 to mesh node
to mesh node 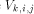 , then up along
, then up along
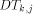
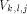 , and finally up along
, and finally up along 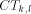 to
to
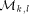 . Similarly, replies go back the same way. Notice that it is not
wise to put all the packets to go trough the root of some
. Similarly, replies go back the same way. Notice that it is not
wise to put all the packets to go trough the root of some 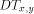 .
.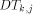 is from one of
the n processors
is from one of
the n processors 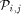 and is destined to one of the n memory modules
and is destined to one of the n memory modules
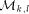 , where
, where 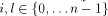 . By Lemma 3 (
. By Lemma 3 (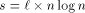 ; the number of
different blanks of n memory modules is
; the number of
different blanks of n memory modules is 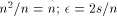 ), we know that at
most
), we know that at
most 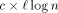 packets enter to
packets enter to 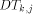 with probability at most
with probability at most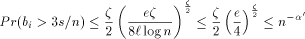
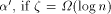 . Clearly, this also
sets a sufficiently large upper bound for q.
. Clearly, this also
sets a sufficiently large upper bound for q.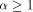 that a 3-dimensional
that a 3-dimensional 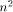 with
with
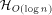 addressing and
addressing and 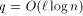 can simulate an
can simulate an 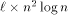 -processor EREW PRAM workoptimally in
-processor EREW PRAM workoptimally in 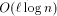 expected routing
steps with probability at least
expected routing
steps with probability at least 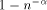 , if
, if 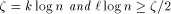 .
.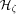 , since we are mainly interested about the routing cost. We
believe that simpler families (e.g.,
, since we are mainly interested about the routing cost. We
believe that simpler families (e.g., 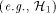 ) can be used in practice
[
) can be used in practice
[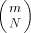
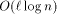 .
.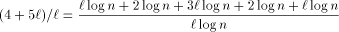
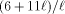 in the 3-dimensional
case. In practice, we suspect that the cost caused by queuing is not
as big as indicated by our naive analysis. Especially, the cost
in the 3-dimensional
case. In practice, we suspect that the cost caused by queuing is not
as big as indicated by our naive analysis. Especially, the cost 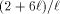 that comes from the depth trees in the 3-dimensional case is too
big. In the next section, we confirm this to be the case.
that comes from the depth trees in the 3-dimensional case is too
big. In the next section, we confirm this to be the case.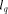 associated
to each directed edge. Our experiments indicated that the size of
associated
to each directed edge. Our experiments indicated that the size of 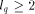 [
[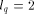 .
.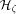 to
define the destinations of packets, since we did not know how to
produce typical access patterns (it makes no sense to apply
to
define the destinations of packets, since we did not know how to
produce typical access patterns (it makes no sense to apply 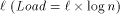 .
.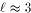 yields cost
yields cost
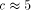 . When
. When 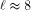 , then the cost
, then the cost 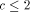 . Furthermore, it seems
that the larger the mesh of trees the lower the simulation cost per
processor. Even though our experiments deal only with relatively small
MTs, we would like to claim that the simulation cost is very small on
large MTs with load
. Furthermore, it seems
that the larger the mesh of trees the lower the simulation cost per
processor. Even though our experiments deal only with relatively small
MTs, we would like to claim that the simulation cost is very small on
large MTs with load 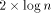 .
.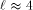 yields cost
yields cost 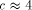 . When
. When 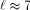 , then the cost
, then the cost
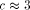 . As in the 2-dimensional case, it seems that the larger the
mesh of trees the lower the simulation cost.
. As in the 2-dimensional case, it seems that the larger the
mesh of trees the lower the simulation cost. 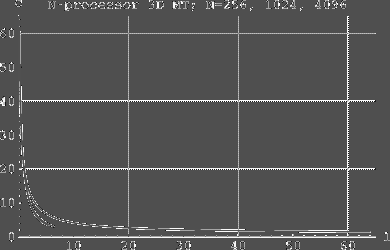
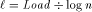 .
.
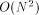 in the
2-dimensional case, and
in the
2-dimensional case, and 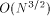 in the 3-dimensional case. For
parameters of our comparison [Tab. 1], we take the routing machinery
size with respect to the number of processors and memory modules;
simulation cost on a quite moderate load; simulation cost on a heavy
load; and the minimum physical distance between logical neighbors. We
note that there exist 'tricks' to improve efficiency, like
integration ofthe routing machinery nodes; faster clockrate in the
routing machinery than in the processors; and delayed memory access
operations. All of them can obviously be used
in the 3-dimensional case. For
parameters of our comparison [Tab. 1], we take the routing machinery
size with respect to the number of processors and memory modules;
simulation cost on a quite moderate load; simulation cost on a heavy
load; and the minimum physical distance between logical neighbors. We
note that there exist 'tricks' to improve efficiency, like
integration ofthe routing machinery nodes; faster clockrate in the
routing machinery than in the processors; and delayed memory access
operations. All of them can obviously be used 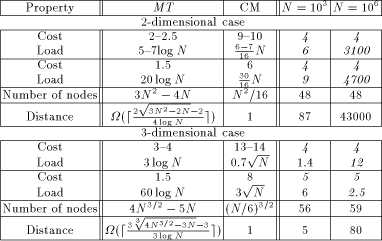
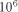 -processor 3-dimensional coated mesh has
only
-processor 3-dimensional coated mesh has
only 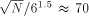 times more routing machinery nodes than
processors. For a corresponding mesh oftrees this ratio is about
4000. Remember that this PRAM simulation approach relies on the
assumption that the routing machinery nodes are considerably simpler
than the processors (and the memory modules). We do not know the
actual difference of the routing machinery nodes and the
processor memory pairs in the hardware complexity, but ratio 70 does
not seem to be totally unacceptable. Especially, if a bunch of routing
machinery nodes (e.g., 8 x 8 x 8) are integrated together to form a
building block of a routing machinery.
times more routing machinery nodes than
processors. For a corresponding mesh oftrees this ratio is about
4000. Remember that this PRAM simulation approach relies on the
assumption that the routing machinery nodes are considerably simpler
than the processors (and the memory modules). We do not know the
actual difference of the routing machinery nodes and the
processor memory pairs in the hardware complexity, but ratio 70 does
not seem to be totally unacceptable. Especially, if a bunch of routing
machinery nodes (e.g., 8 x 8 x 8) are integrated together to form a
building block of a routing machinery.