| Submission Procedure |
Replication: Understanding the Advantage of Atomic Broadcast over Quorum SystemsRichard Ekwall André Schiper Abstract: Quorum systems (introduced in the late seventies) and atomic broadcast (introduced later) are two techniques to manage replicated data. Despite of the fact that these two techniques are now well known, the advantage of atomic broadcast over quorum systems is not clearly understood. The paper explains exactly in what cases atomic broadcast is a better technique than quorum systems to handle replication. Key Words: atomic broadcast, quorum systems, replication, isolation 1 IntroductionThe requirement for highly reliable and available services has been continuously increasing in many domains for the last decade. Several approaches for designing fault-tolerant services exist. The focus in this paper is on software replication. Replication allows a number of replicas to crash without affecting the availability of the service. Quorum systems was the first technique introduced to manage replication [14, 5]. Since this period, a lot of progress has been accomplished in the understanding of the problems related to replication. An important step has been the introduction of group communication, which defines a middleware layer that hides most of the hard problems related to replication [12]. The advent of group communication has temporarily led to a decrease of interest in quorum systems. However, there has been recently a renewed interest in quorum systems for Byzantine faults [11], an issue not addressed previously. Moreover, there are now here and there people disagreeing on the advantage of group communication over quorum systems for replication. The goal of the paper is to clarify this issue, and point out precisely when and why group communication is a better solution.
Research supported by OFES under contract number 01.05371 as part of the IST REMUNE project (number 200165002). Page 703 The rest of the paper is organized as follows. Section 2 introduces our system model and three isolation degrees, a key issue to understand the respective scope of quorum systems and atomic broadcast. Section 3 discusses the absence of isolation requirements. Section 4 discusses the case when only read-write isolation is required. Section 5 discusses general isolation requirements. Finally, Section 6 concludes the paper. 2 Different isolation degreesIn the context of replication, one of the key issues is the semantics that has to be provided. We consider in the paper a finite set of processes, where each process issues a sequence of operations over a finite number of replicated data. Without restriction to generality, we consider that each operation is either a read or a write. A read operation reads one replicated data; a write operation writes one replicated data. The semantics defines the result of each of these read and write operations. One key aspect of the semantics is the isolation property, as defined in the context of database systems [15]. We distinguish the following degrees of isolation:
To illustrate the three cases, consider two processes p, q, two replicated data X, Y, and the following sequences of operations: 1
With no isolation, any interleaving of operations of the two processes is possible. We express isolation using [ . . . ] brackets. Here is the same same sequence of operations with readwrite isolation (the consecutive readwrite operations are executed in isolation):
1rp(X) (respt. wp(X)) denotes a read (respt. a write) of data X by process p. Page 704
Finally, general isolation allows us to specify for example the following isolation requirement:
3 No isolationRead-write operations with no isolation corresponds to the notion of
register [10]. The strongest register semantics, called
atomic register, ensure that the read and write operations behave
as if each operation op issued by process p happened instantaneously at
some time t Atomic registers can be implemented in an asynchronous system (which is defined as a system in which there is no bound on the transmission delay of messages, nor on the relative speed of processes). Quorums are here well suited to implement atomic registers. As an example, consider the data X replicated on several servers Xi, where each server Xi manages (1) a copy of the data and (2) a version number. A quorum is defined as any subset of servers. Quorum systems distinguish read quorums and write quorums, which must satisfy the following properties [5]:
Let n be the number of replicas. One standard way to satisfy these properties is the following [5]:
The operation wp(X Page 705 The read operation rp(X) is slightly less intuitive: (1) the client reads the pair (value, version) from a read quorum, (2) the read operation returns the value val with the highest version number, and finally (3) the value val is written to a write quorum. 2 The specificity of this solution can be summarized as follows: (1) data is sent back and forth between the servers Xi and the client process p, and (2) servers only send and receive data. We will come back to this point later. 4 ''Read-write'' isolation onlyTo show the limitations of the atomic register semantics, and the need for read write isolation, consider the following sequence of operations, where process p wants to increment X, while process q wants to decrement X . If X is initially 0, then without readwrite isolation, the following execution is possible: 3
This execution is clearly not desired (the final value of X must be 0). A correct execution requires that p and q execute the readwrite sequence in mutual exclusion, i.e., in isolation. This can be expressed as follows, where ECS/LCS allows a process to enter/leave the critical section:
4.1 Readwrite isolation and the consensus problemWe first show that readwrite isolation cannot be solved in an asynchronous system with crash failures. Then we discuss the implementation of readwrite isolation (1) with quorum systems and (2) with atomic broadcast (a group communication primitive). Consensus is a well known problem defined over a finite set of processes, in which each process has an initial value and all processes that do not crash have to agree on a common value that is the initial value of one of the processes [1]. Consensus is not solvable in an asynchronous system if processes may crash [4]. This impossibility also applies to readwrite isolation; it follows directly from the fact that readwrite isolation is powerful enough to solve consensus (see also [8]).
2Without (3), the atomic register semantics is not ensured. To see this, consider (a) wp1 (X  w) by p1
that starts at t = 1 and ends at t = 6, (b) a read operation
rp2 (X) by p2 that
starts at t = 2, reads w, and terminates at t = 3,
and (c) a read operation rp3 (X) by p3
that starts at t = 4 and ends at t = 5. Without (3), p3
could read an old value rather than w, which is required by the
atomic register semantics. w) by p1
that starts at t = 1 and ends at t = 6, (b) a read operation
rp2 (X) by p2 that
starts at t = 2, reads w, and terminates at t = 3,
and (c) a read operation rp3 (X) by p3
that starts at t = 4 and ends at t = 5. Without (3), p3
could read an old value rather than w, which is required by the
atomic register semantics. 3rp( 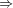 v) denotes a read operation that returns the value v.
v) denotes a read operation that returns the value v. 4rp(X  u)
denotes that the value returned by the read operation is stored into the
local variable u. u)
denotes that the value returned by the read operation is stored into the
local variable u.
Page 706 To show this, consider consensus to be solved among n processes p1 , . . . , pn, with val i the initial value of process pi. Let the data be here a vector V of n + 1 elements V[0], . . . , V[n]. Initially, we assume V[0] = 0, and all other elements V[j] undefined. Each process pi executes Algorithm 1, where V[0] is incremented and V[V [0]] written inside a critical section (lines 2-5).
Algorithm 1: Solving consensus with readwrite isolation: code of process pi If at least one process pi is correct, then V[1] is written (with the initial value of one of the processes). Moreover, since all processes decide on the value V[1], they all decide the same value, which is the initial value of one of the processes. So readwrite isolation allows us to solve consensus, which shows the contradiction, i.e., read-write isolation cannot be implemented in an asynchronous system with process crashes. 4.2 Implementing readwrite isolation with quorumsSince read-write isolation cannot be implemented in an asynchronous system with process crashes, we need additional assumptions. The quorum solution of Section 3 can be extended to provide read-write isolation if we can solve the mutual exclusion problem. Implementing mutual exclusion requires to handle the following situation:
In this case, p will never release the critical section, i.e., the critical section must be released on behalf of p. This requires a crash detection mechanism that detects the crash of p if and only if p has crashed (the critical section must be released if and only if p has crashed). This corresponds to a perfect failure detector [1], which is a strong requirement. Note that in addition to a perfect failure detector, if the read/write quorums are defined as in Section 3, the solution also requires a majority of correct processes (to always ensure the existence of a read quorum and of a write quorum). Page 707 4.3 Implementing readwrite isolation with atomic broadcastWe now describe a different solution to read-write isolation, which uses a group communication primitive, namely atomic broadcast (also called total order broadcast). Atomic broadcast allows to broadcast messages to a group of processes, while ensuring that messages are delivered by all members of the group in the same order. A formal definition can be found in [7, 3]. To show the implementation of read-write isolation with atomic broadcast, we model the execution of each process as follows:
Algorithm 2: Model for read-write isolation: code of process p Process p first reads X into a local variable u, then does some local computing expressed by the function f(u), and finally writes the new value of u to X . With atomic broadcast, denoted by ABcast( ), the above schema can be implemented as follows, using a technique called state machine approach [9, 13]. The technique distinguishes between (1) the code of process p (Algorithm 3) and (2) the code of a server X i that manages a copy xi of the data X (Algorithm 4).
Every server Xi receives the update functions f
in the same order, and up-dates its copy xi using the same update
function. Moreover, each server xi executes one update function
before considering the next one. So Algorithms 3 and
4 correctly implement atomic registers with read-write
isolation. Indeed, the solution requires to solve atomic broadcast. Atomic
broadcast is solvable in an asynchronous system augmented with the failure
detector
5 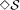 S satisfies the following properties: (1) Eventually every process in gX
that crashes is permanently suspected by every correct process in gX
, and (2) there is a time after which some correct process in gX
is never suspected by any correct process in gX [1].
S satisfies the following properties: (1) Eventually every process in gX
that crashes is permanently suspected by every correct process in gX
, and (2) there is a time after which some correct process in gX
is never suspected by any correct process in gX [1].
Page 708 4.4 DiscussionIf we compare the requirements of the quorum solution and of the atomic
broad-cast solution, we observe the following. The two solutions require
a majority of correct processes; the quorum solution requires a perfect
failure detector, while the atomic broadcast solution only requires the
weaker failure detector What makes the difference? In the quorum solution, the update function f is executed by the client process itself. In the atomic broadcast solution, the update function f is executed by the servers. The former solution requires (1) mutual exclusion, and (2) to send data back and forth between the client and the servers. The atomic broadcast solution requires only to send the update function f to the servers. Executing f on the servers is a more clever solution than executing f on the client! 5 General isolationWe now discuss the implementation of general isolation. The quorum solution can trivially be extended to handle general isolation. Indeed, whether mutual exclusion protects two operations or more than two operations makes no difference. Can the atomic broadcast solution be extended to handle general isolation? Yes, if specific conditions are met (which also means that the solution is not always applicable):
The atomic broadcast solution may also require atomic broadcasts to multiple groups [6]. We now give two examples where these conditions are satisfied. Page 709 Example 1: Consider two replicated data X and Y, representing two bank accounts. Assume a user that wants to withdraw an amount w from account X and deposit w on the account Y. This can be expressed by the following update function: f The user simply issues ABcast(f) to gX Example 2: Let us modify slightly Example 1, such that the transfer
of w from account X to account Y takes place if and
only if X f This leads to the following problem: while a server xi
can evaluate the condition X In these two examples the set of data to be accessed is known statically. If this condition is not met, which is quite common in the case of database transactions, then the atomic broadcast solution cannot be used (since it cannot be known to which servers to send the update function). Note that the function could be sent to all servers, but this solution might be too costly or even impossible to implement. 6 ConclusionThere is a common misunderstanding of the advantage of group communication over quorum systems to manage replicated data. We have tried to clarify this issue by showing the basic difference between the two techniques: when isolation needs to be provided, group communication consists in sending the update func tion to the data servers, while with quorum systems servers send the data to the clients where the update function is performed. The first solution requires weaker extensions to the asynchronous system, and so has obvious advantages. We have also shown that the use of group communication is not restricted to read-write isolation. This contradicts the claim of Cheriton and Skeen in [2] in the context of the CATOCS controversy,6 where they write that CATOCS cannot ensure serializable ordering between operations that correspond to group of messages (...)
6CATOCS = Causally and totally ordered communication support. Page 710 Locking is the standard solution.7 As shown, this argument is not correct. Apart from this specific issue, we believe that the paper should allow in the future to clearly understand the merits of group communication over quorum systems to manage replication. References1. T. D. Chandra and S. Toueg. Unreliable failure detectors for reliable distributed systems. Journal of ACM, 43(2):225-267, 1996. 2. D. R. Cheriton and D. Skeen. Understanding the Limitations of Causally and Totally Ordered Communications. In 14th ACM Symp. Operating Systems Principles, pages 44-57, Dec 1993. 3. X. Défago, A. Schiper, and P. Urban. Total Order Broadcast and Multicast Algorithms: Taxonomy and Survey. ACM Computing Surveys, 36(2):372-421, December 2004. 4. M. Fischer, N. Lynch, and M. Paterson. Impossibility of Distributed Consensus with One Faulty Process. Journal of ACM, 32:374-382, April 1985. 5. D.K. Gifford. Weighted Voting for Replicated Data. In Proceedings of the 7th Symposium on Operating Systems Principles, pages 150-159, December 1979. 6. R. Guerraoui and A. Schiper. Genuine atomic multicast in asynchronous systems. Theoretical Computer Science, 254(1-2):297-316, January 2001. 7. V. Hadzilacos and S. Toueg. Fault-Tolerant Broadcasts and Related Problems. Technical Report 94-1425, Department of Computer Science, Cornell University, May 1994. 8. M. Herlihy. Impossibility and universality results for wait-free synchronization. In Seventh ACM Symposium on Principles of Distributed Computing (PODC), pages 276-290, August 1988. 9. L. Lamport. Time, Clocks, and the Ordering of Events in a Distributed System. Comm. ACM, 21(7):558-565, July 1978. 10. L. Lamport. On interprocess communications, i, ii. Distributed Computing, 1(2):77-101, October 1986. 11. D. Malkhi and M. Reiter. Byzantine Quorum Systems. Distributed Computing, 11(4):203-213, 1998. 12. A. Schiper. Practical Impact of Group Communication Theory. In Future Directions in Distributed Computing, pages 1-10. Springer, LNCS 2584, 2003. 13. F. B. Schneider. Replication Management using the State-Machine Approach. In Sape Mullender, editor, Distributed Systems, pages 169-197. ACM Press, 1993. 14. R.H. Thomas. A Majority Consensus Approach to Concurrency Control for Multiple Copy Databases. ACM Trans. on Database Systems, 4(2):180-209, June 1979. 15. G. Weikum and G. Vossen. Transactional Iinformation Systems. Morgan Kaufmann, 2002.
7Note that atomic broadcast can be used for locking Page 711 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [opstart, opend] , where opstart
is the time at which the op is issued by process p, and opend
is the time at which op has completed on p [
[opstart, opend] , where opstart
is the time at which the op is issued by process p, and opend
is the time at which op has completed on p [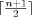 .
.
 u), u
u), u  ( sub(X, w); add(Y, w) )
( sub(X, w); add(Y, w) )  gY,
where gX, respt. gY, are the group
of replicas of X, respt. Y. Upon delivery of f a server
Xi decrements its local copy xi by
w, and a server Yi increments its local copy yi
by w.
gY,
where gX, respt. gY, are the group
of replicas of X, respt. Y. Upon delivery of f a server
Xi decrements its local copy xi by
w, and a server Yi increments its local copy yi
by w. 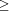 w. This can be expressed as follows:
w. This can be expressed as follows: